面向多核任务调度的混合遗传算法

姚英彪，王 璇

（杭州电子科技大学通信工程学院，浙江杭州310018）

面向多核任务调度的混合遗传算法

姚英彪，王 璇

（杭州电子科技大学通信工程学院，浙江杭州310018）

多核处理器的并行任务调度一直是研究的热点话题，属于NP-hard问题。针对此问题，本文提出了一种集启发式算法、禁忌搜索算法、模拟退火算法于一体的改进混合遗传算法（modified hybrid genetic algorithm，MHGA）。MHGA改进如下：首先，采用启发式的分层调度来初始化种群，提高初始种群质量；其次，提出基于禁忌搜索（tabu search，TS）的随机编号交叉算子，提高种群的多样性；最后，采用基于模拟退火（simulated annealing，SA）的变异，提高个体质量。实验结果表明，与其他遗传算法（genetic algorithm，GA）相比，MHGA可以得到更小的任务调度时间和更快的最优解搜索能力。

遗传算法；禁忌搜索；模拟退火；并行调度；多核处理器

0 引 言

在多核系统芯片（multi-processor system-on-chip，MPSoC）设计中，如何进行任务分配和调度是一个非常关键的问题，这个问题可以简单描述为：N个有前后依赖关系的任务如何分配到P个处理器上执行，在保证任务依赖关系的条件下使得任务总完工时间最小。任务分配解决在哪个处理器核上执行任务，即匹配任务到处理器核上；任务调度解决何时执行任务，即给出任务在具体处理器核上的起止时间。影响任务分配和调度的因素主要有：任务计算时间、任务之间的依赖关系和处理器核之间的数据传输延迟等。国内外学者对这个问题进行了深入的研究，研究结果表明多核任务分配和调度问题是一种组合优化问题，不能在多项式时间复杂度内找到最优解，已被证明是NP-hard问题［1－4］。

目前解决这个问题的方法大致可以划分为启发式算法和智能搜索算法两类。启发式算法一般采用某种启发规则进行任务的分配和调度，它一般只能找到问题的次优解，且在求解大规模任务分配和调度问题时，得到的解往往与最优解相差甚远。它的优点在于复杂度低，可以快速给出某种次优结果。启发式算法的代表有修改关键路径算法［5］（modified critical path，MCP）、异构最早完成时间算法［6］（heterogeneous earliest finish time，HEFT）等。智能搜索算法是一种利用自然现象与优化过程的某些相似性而逐步发展起来的搜索方法，其算法思想简单，同时还具备搜索全局最优解的能力。遗传算法（genetic algorithm，GA）［7－9］、模拟退火（simulated annealing，SA）［10］、粒子群算法（particle swarm optimization，PSO）［11］、禁忌搜索（tabu search，TS）［12］等都属于智能搜索算法。

本文计划采用遗传算法框架解决MPSoC的任务分配和调度问题。文献［13］率先将GA应用到并行任务调度中，奠定了用GA解决此类问题的基础。但是，传统GA也碰到了下面3个主要难题：①问题描述困难，②初始化种群质量难以保证，③容易早熟，造成进化后期搜索效率较低。因此，GA的改进可以从优化初始种群［14］、改进编码机制［15］、改进遗传算子［16］、防止种群早熟［17］等方面进行。

针对传统GA碰到的问题，本文提出一种集启发式调度、TS、SA于一体的改进混合遗传调度算法（modified hybrid genetic algorithm，MHGA）：①采用启发式的分层调度来初始化种群，提高初始种群质量；②提出基于TS的随机编号交叉算子，使用禁忌表来封锁刚搜索过的区域从而避免迂回搜索，同时赦免禁忌区域中的一些优良状态，保证搜索的多样性，从而提高种群的多样性；③在对个体进行变异时，采用SA对个体进行变异，提高种群中每个个体的质量。本文实验结果表明，与其他GA相比，MHGA可以得到更小的任务调度时间和更快的最优解搜索能力。

1 任务模型及算法框架

1.1 任务模型

任务模型用有向无环图（directed acyclic graph，DAG）来表示，即G＝〈T，E〉。其中，T为任务节点的集合，T＝｛i｜1≤i≤N｝表示N个任务的集合；E＝｛eij｝为任务之间有向边的集合，边eij表示任务i执行后才可以执行j。同时假设t＝｛t1，t2，…，tN｝表示任务的执行时间；c＝｛cij｝为任务之间有向边eij的权重，cij表示任务i和j分配到不同处理器时的通信时间；当任务i和j分配到同一处理器时，通信时间为0。一个简单的11个任务的DAG图如图1所示（图1中，每个任务的执行时间为2，任务间的通信时间为1）。

图1 任务DAG图

1.2 算法框架

对于已知的DAG图，可以根据任务之间的依赖关系定义任务层级值h，表示任务节点的层数，定义如下：

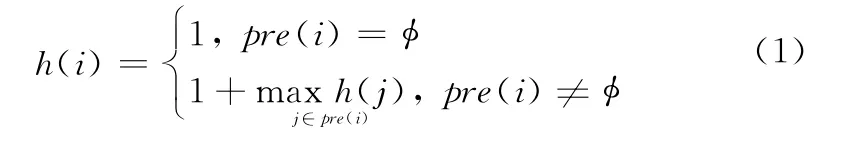
本文提出的MHGA算法由节点层级值计算、初始种群生成、轮盘赌选择、禁忌搜索交叉、模拟退火变异组成。算法的框架图如图2所示。

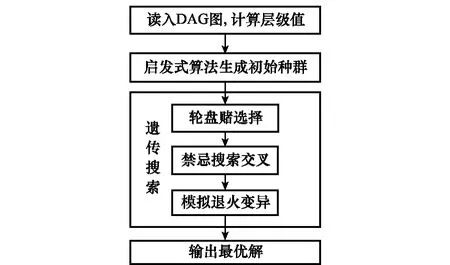
图2 算法框架图

2 MHGA算法设计

2.1 初始种群生成

为提高初始种群质量，本文采用基于层级值h的分层调度启发式算法来生成初始种群，替代传统的完全随机的初始种群。

2.1.1 任务的初始处理器分配

对于一个特定的DAG图，根据式（1）可以算出每个任务的层级值h。图1中，任务的层级值依次为｛1；2，2；3，3；4，4，4；5，5；6｝，不同层级值的任务用分号隔开。将所有任务按照层级值进行分层，层级值相同的任务放在同一层，第j层的任务集合为Tj＝T｛h＝j｝。因此，图1可以分为6层，分别为T1＝｛1｝，T2＝｛2，3｝，T3＝｛4，5｝，T4＝｛6，7，8｝，T5＝｛9，10｝，T6＝｛11｝。

从图1可以看出，具有相同层级值的任务可以并行执行。因此，为降低任务的完工时间，应该尽量将每层的任务均衡地分配到处理器上。假设处理器总数为P，每层的任务总数为n，则n／P＝a…b（其中b为余数）。在总任务中随机选取b个任务（b＜P）随机分配到不同的处理器；对于剩下的a×P个任务，每个处理器从中随机选择a个任务。这样可以确保将每层任务均衡的分配到处理器上，避免同一层任务过多集中在一个处理器上造成完工时间的延迟。

图1的DAG图，设其处理器总数P＝2。对于T4＝｛6，7，8｝，n／P＝3／2＝1…1，先任选1个任务分配给任一个处理器，例如把任务8分配给处理器P1；剩下的任务均衡分配给P1和P2；这样T4可能的一个处理器分配为｛p1，p2，p1｝。根据以上处理器分配原则，图1所示的11个任务的一个可能的处理器初始分配p＝｛p1；p1，p2；p1，p2；p1，p2，p1；p2，p1；p1｝。

2.1.2 任务的编码

本文采用符号编码方案，符号由任务的基因值组成，所有任务的基因序列构成一个染色体（或个体）。任务基因值产生包括两个阶段：

步骤1 基因值初始化阶段，即由初始处理器分配序列得到初始基因值序列。这一阶段采用固定映射方式，映射规则如下：

式中，vi为任务i的基因值；pi为任务i初始分配处理器号；P为处理器总数。上述规则能够保证个体中的每个基因值都唯一，即每个任务的基因值都不相同。这样可以保证后面（2.1.3节）根据基因值进行任务调度时，能够得到唯一的调度方案。

步骤2 基因值随机交换阶段，即对每个处理器上的任务的基因值进行随机交换。交换规则如下：假设某个处理器上共分配m个任务，随机选取该处理器上两个任务，将其基因值进行交换，重复进行 m／2 次交换；对每个处理器都执行上述操作，最终得到新的染色体。

进行此阶段的原因在于，依据式（2）得到的任务的基因值跟任务序号成正比，是逐渐递增的，不具有随机性，减小了初始种群的空间的大小。随机交换后，任务的基因值与其序号不在具有对应关系，具有更好的随机性。

上节所示的处理器初始分配序列p＝｛p1；p1，p2；p1，p2；p1，p2，p1；p2，p1；p1｝，根据式（2）初始化后得到的个体为V＝｛3；5，8；9，12；13，16，17；20，21；23｝；随机交换后，可能的一个个体为V＝｛23；5，20；13，16；9，12，21；8，3；17｝。此时，任务1到11对应的基因值分别为23，5，20，13，16，9，12，21，8，3，17。

2.1.3 任务调度与分配

得到个体V后，采用基于任务的层级值和基因值的任务调度、基于任务基因值的处理器分配。

任务调度规则：首先，对于不同层级值的任务，按照任务的层级值从小到大进行调度，也就是说，层级值较小的所有任务都调度完成才能调度层级值较大的任务；其次，对于相同层级值的任务，按照任务的基因值从大到小进行调度。

根据以上规则，个体V＝｛23；5，20；13，16；9，12，21；8，3；17｝的调度顺序TS为：1→3→2→5→4→8→7→6→9→10→11。

处理器分配规则：任务的基因值和处理器总数取余即为任务分配的处理器，如式（3）所示，其中mod代表取余。

上述个体进行处理器分配后，可得到任务1，2，4，6，8，10和11在p1上执行，任务3，5，7和9在p2上执行。可以发现，由式（3）得到的处理器分配序列和该个体对应的初始处理器分配序列p＝｛p1；p1，p2；p1，p2；p1，p2，p1；p2，p1；p1｝仍然一致，这是因为：式（3）是式（2）的反变换，同时，上一节基因值随机交换只针对同一个处理器上的任务进行，它不改变任务分配的处理器结果。

对该个体，在两个处理器上的任务调度顺序可以表示成：

2.1.4 任务开始时间和完工时间

按照任务在调度序列TS的顺序，依次计算每个任务开始执行时间和完工时间，可得到每个处理器的完工时间和任务的总完工时间。假设TS序列中第q个执行的任务为i，其分配到的处理器为pi，任务i能够开始执行的先决条件是其资源约束和依赖约束同时被满足，具体如下：

（1）资源约束规则。由于每个处理器一个时刻只能执行一个任务，即分配到pi上的任务调度序列必须顺序执行，因此i在pi上的开始时间必须不小于i前一个任务k的完工时间。假设k的开始时间为sk，执行时间为tk，则该约束确定的i的开始时间应该满足：

（2）依赖约束规则。任务i能在pi开始执行的另一个约束为其前继任务集合pre（i）中的每一个任务j都完成，且当i与j不在同一个处理器时，i与j之间的通信任务也必须完成，即要满足任务之间的前后依赖关系。根据该约束确定的i的开始时间应该满足：

最后，根据上述两个规则确定的任务i的最早开始执行时间为

在得到每个任务的开始执行时间和完工时间后，就可以给出任务的分配和调度图。图3给出图1所示11个任务的一个可能分配和调度图。

图3 任务分配和调度图

2.1.5 初始种群优化

为更好地生成高质量的初始种群，本文还进行了初始种群优化，其思想是在完工时间最长的处理器plong上选取一个任务分配到完工时间最短的处理器pshort上，重复进行若干次。具体步骤如下：

步骤1 若plong上存在一个任务i，使得i与在i后执行且分配到plong的所有任务都没有前后继依赖关系，那么将i分配到pshort上，这样明显可以缩短完工时间；若不存在这样的i，则在plong上随机选取一个任务分配到pshort上。

需要注意的是，由于任务i的处理器分配发生了改变，必须修改任务i的基因值。假设任务i原基因值为vi，原分配的处理器号为pi，新分配的处理器号为p′i，则新基因值v′i如式（7）所示。

这样，不仅任务的新基因值和分配到的处理器符合式（3），同时保证了新基因值不会与其他任务的基因值重复，确保了基因值的唯一性。同时可以证明，该层的任务调度序列不会发生改变，因此总的任务调度序列不变。

步骤2 计算新个体的任务完工时间并与原来的完工时间进行对比，如果新完工时间更短，则用新个体代替原个体；反之，保持原个体不变。

图3所示调度中，p1上不存在任务i，使得i与在i后执行且分配到p1的所有任务都没有前后继依赖关系。所以只能在p1上随机选取一个任务（假设选择了任务6），重新分配到p2上。任务6的原基因值为9，因此新基因值为9＋2－1＝10。同h值有6，7，8三个任务，该层的基因序列由｛9，12，21｝变为｛10，12，21｝，依据第2.1.3节得到该层的调度顺序仍为：8→7→6，没有发生改变，因此总的任务调度序列TS保持不变。由此可以得到新的调度图，如图4所示，任务的完工时间由18变为16，得到了优化，因此用该新个体代替原个体。

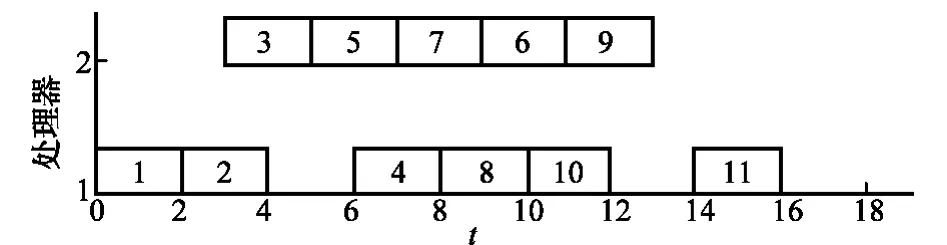
图4 重新调度的任务图

步骤3 重复前两步，进行足够多次后（本文取10次）就可以得到较优个体。

以上3步，可以有效地减少个体的总完工时间，提高个体质量。对种群中所有个体进行相同的操作，这样就可以得到高质量的初始种群。图5为初始种群的流程图。

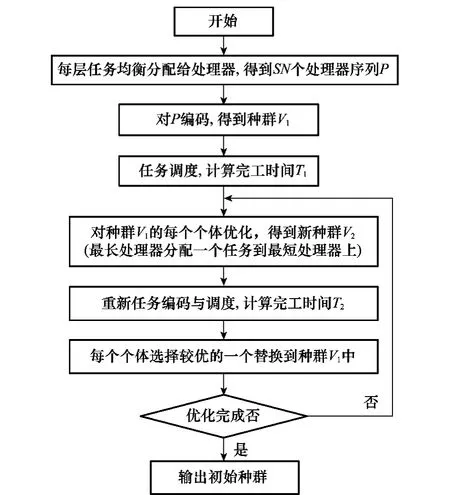
图5 初始种群流程图

2.2 适应度函数

适应度函数表示个体对生存环境的适应能力，个体的适应度越大，则该个体被遗传到下一代的概率就越大。对于多核处理器的任务调度，可以用总任务的完工时间（也就是最后一个执行的任务的完成时间）来评价其适应能力，个体Vi适应度函数如下：

式中，span（Vi）表示个体Vi的完工时间，图4中任务的完工时间为16。

2.3 遗传搜索过程

2.3.1 轮盘赌选择

选择是从当前种群中选取适应值高的个体进行交叉、变异，将优良基因遗传给后代。本文用轮盘赌旋转法进行选择，如图6所示，方法如下：

（1）在［0，1］区间内产生一个均匀分布的随机数r；（2）若r≤q（1），则个体V1被选中；

（3）若q（k－1）＜r≤q（k）（2≤k≤SN，SN为种群规模），则个体Vk被选中。

其中，q（i）为染色体的累计概率，计算公式为

P（Vi）为个体Vi被挑选的概率，其公式为

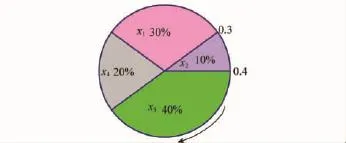
图6 轮盘赌选择

2.3.2 基于TS的随机编号交叉

交叉可以增加种群多样性，提高种群搜索能力。鉴于GA的广域搜索能力较强，TS的局部搜索能力较强，可以将两者混合对交叉操作进行改进，也就是把TS的“禁忌”和“特赦”思想引入到GA的交叉步骤中。

基于TS的随机编号交叉步骤如下：

步骤1 初始化。规定种群中所有个体的最大适应度值为初始渴望水平；个体的适应度值为禁忌表中的元素；禁忌表长度为l。

步骤2 根据交叉率选择相邻两个父代进行基于随机编号交叉操作，产生两个子代。对于进行交叉的两个个体V1，V2，在V1中随机选择一个初始交叉点和截止交叉点，交叉总任务数为l，该初始交叉点和截止交叉点也是V2的初始交叉点和截止交叉点。将V1截取的一小段个体的l个任务随机编号1～l；V2同理。然后，将这两小段编号一样的任务的基因值进行交换，最后再将这两小段整体互换，这样就可以得到新的个体S1，S2，如图7所示。

图7 基于随机编号的交叉

步骤3 如果子代个体适应度值大于渴望水平，则破禁，该个体进入下一代；同时，更新禁忌表和渴望水平，将该个体的适应度值设为新的渴望水平。

步骤4 如果没有破禁，检测子代个体适应度值是否在禁忌表中。如果不在，该个体进入下一代，同时更新禁忌表；反之，舍弃该个体，选择相应的父本进入下一代。

步骤5 返回步骤2，直至种群中所有个体完成交叉。

2.3.3 基于SA的变异

变异提供给种群新的基因，提高了种群的多样性。GA的局部搜索能力差，变异后个体的质量不高；将SA算法添加到遗传算法中，利用SA算法局部搜索能力强的优点，优化每个个体的质量。

基于SA的变异步骤如下：

步骤1 初始化。在种群中随机选取个体Vi为初始解。给定初始温度T0，终止温度Tf，降温值ΔT，内循环次数n（Tk）。令Tk＝T0，最优解Vbest初始化为Vbest＝Vi。

步骤2 对个体Vi进行变异，变异后的个体为Vj，则完工时间增量Δf＝span（Vj）－span（Vi）。

变异步骤：在个体V中，随机选择两个不同的变异点，然后交换其基因值，就可以得到一个新的个体S，如图8所示。

图8 变异

步骤3 如果Vj的完工时间小于Vbest的完工时间，更新Vbest＝Vj。

步骤4 若Δf＜0，则无条件转移：Vi＝Vj；若Δf＞0，则进行有条件转移：随机产生一个随机数ξ＝U（0，1），如果则Vi＝Vj，反之Vi保持不变。

步骤5 若达到热平衡状态（内循环次数大于n（Tk）），进行步骤6，否则转步骤2。

步骤6 降低Tk，降温函数为：Tk＝Tk－ΔT。若Tk＜Tf，则算法停止，输出Vbest；否则转步骤2。

对交叉后的种群中的每个个体都进行上述操作，最终可以得到变异后新的种群。通过SA，新种群中每个个体的适应度值均得到有效的提高，避免了常规变异造成个体变差的可能性，提高了GA的性能。

2.3.4 变异后调度图

需要注意的是，变异使得某些任务的基因值发生了改变，这些任务分配到的处理器也就相应地发生变化，由式（3）可得到这些任务分配到的新处理器。根据第2.1.3节，可得到任务调度序列TS；根据第2.1.4节可得到新一代种群中所有个体的任务调度图，也就知道了其最优个体完工时间。

2.3.5 算法结束

重复进行上述步骤到规定的代数，就可以得到最优任务调度图及最短完工时间。图1的DAG图，根据上述算法，得到的最优调度图如图9所示，其完工时间为14。

图9 最优调度图

本文所述的遗传算法流程图如图10所示。

图10 遗传算法流程图

3 仿真实验

3.1 实验参数

在进行仿真实验时，可以随机生成DAG图，规定所有任务的计算时间总和与通信开销的总和的比值为0.5，且每个任务的计算时间和任务间通信时间的取值范围为［2，20］，其他仿真实验参数如表1所示。用MATLAB 2012b进行仿真，并将本文的MHGA算法和标准HGA算法［13］、Hwang的PGA算法［15］进行比较。为了消除数据随机性对结果的影响，将实验数据取30次平均，可以得到最终的对比结果。

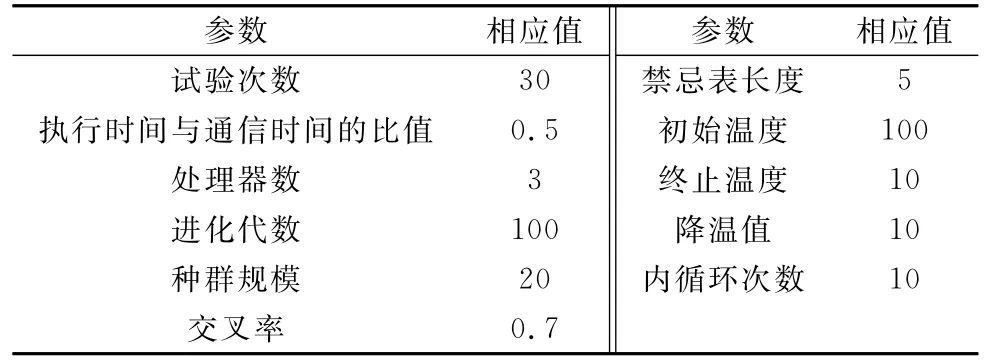
表1 实验参数设定

3.2 仿真结果

本文提出的MHGA算法使用了初始化种群和混合遗传算法两部分操作，为了更好地研究MHGA的性能，这里将该算法拆分成两部分。MHGA-1只进行初始化种群，没有采用改进混合遗传算法；MHGA-2只进行改进混合遗传算法，没有初始化种群。

图11是不同任务数完工时间的比较。从图11中可以看到，本文提出的MHGA算法得到的完工时间是最优的，即MHGA寻找最优解的能力最强。PGA次之，HGA搜索最优解的能力最差。MHGA相比于MHGA-1，性能得到较大提高；相比于MHGA-2相差不多，但也得到了改善。

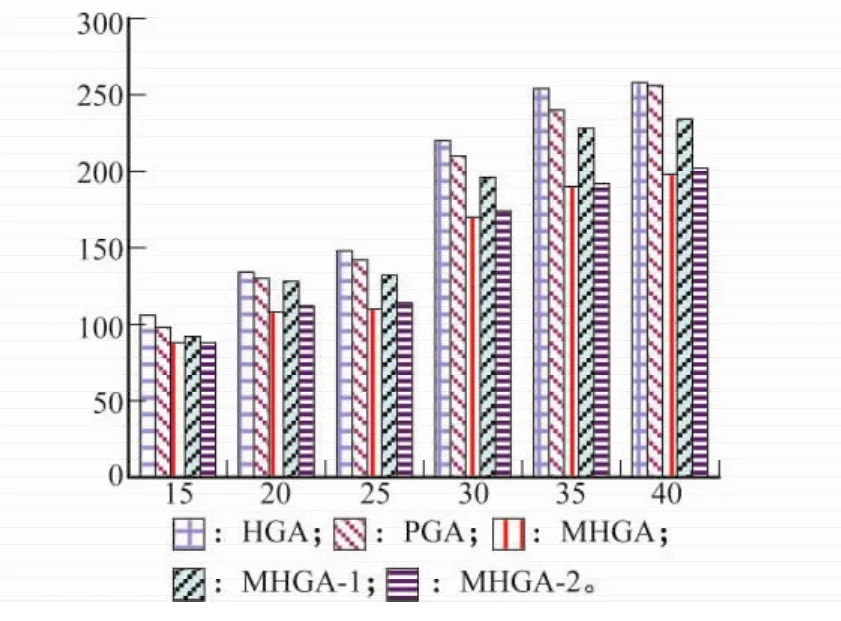
图11 不同任务数的完工时间比较

图12为3种算法在100代的完工时间收敛过程。从图12可以看出，在收敛值方面，本文提出的MHGA算法的收敛值明显优于HGA和PGA；在收敛速度方面，HGA最快，MHGA次之，PGA最慢。HGA算法因为其过早收敛，造成其收敛值最大，即搜索最优解能力最差。PGA算法不仅收敛较慢，其收敛值也高于MHGA算法。由于MHGA优化了初始种群，使用了混合遗传算法，导致此算法整体上每代结果均优于其他两种算法。

图12 最小完工时间的收敛过程

MHGA-1只初始化了种群，尽管在第一代的结果较优，但随着代数的增加，其搜索能力变差且收敛速度较慢。MHGA-2采用了混合遗传算法，使得种群多样性增加，个体的适应度值也得到提高。随着代数的增加，其最优解的搜索能力逐渐变好。由于没有初始化种群，使得收敛值大于MHGA，且收敛速度较慢，搜索时间更长。而本文的MHGA综合了MHGA-1和MHGA-2两者优点，不仅收敛值更优，其收敛速度也得到了提高，提升了遗传算法的性能。

以上是取30次实验求平均得到的结果，为了更好地分析每次遗传的情况，随机选取1次实验来进行分析（N＝35），由此可以得到每代的任务完工时间，如图13所示（图13中，MHGA算法输出的每代完工时间是图10中种群S3的最优个体的完工时间）。

图13 每代的完工时间（N＝35）

由图13可以看出，HGA算法每代结果的动态范围最小，其算法达到较优结果后，很难再跳出去，从而使得算法早熟，其结果易于陷入局部最优。PGA算法采用了基于优先级的编码（priority-based multi-chromosome，PMC）、权重交叉（weight mapping crossover，WMX）等操作，使得算法每代结果的动态范围最大，可以避免算法早熟，但其收敛速度较慢，且得到的最优解较差。MHGA-1初始化了种群，尽管第一代的结果较优，但最优解的搜索能力较差。MHGA-2采用混合遗传算法，但由于没有初始化种群，其搜索时间更长，收敛速度较慢，最优解也差于MHGA。MHGA综合了MHGA-1和MHGA-2的优点，不仅收敛值更优，其收敛速度也得到了提高。

4 结束语

本文提出的MHGA在解决并行多核任务的分配和调度时，其性能优于其他算法的原因在于：首先利用启发式方法对初始种群进行分层分配和调度，产生质量较高的初始种群；其次，使用基于TS的随机编号交叉，提高了种群的多样性；最后，采用基于SA的变异，提高个体的质量，所有个体的适应度值得到了提高。仿真结果表明，MHGA能够得到更短的任务完工时间，具有较强的最优解搜索能力，可用于实际应用。当然，MHGA也有不足，主要表现在：①仅适用于同构MPSoC系统；②算法参数不能够自适应调整。因此，未来希望将本文算法扩展到异构多核系统中，同时一些关键参数能够自适应调整，从而增强MHGA的适用范围和性能。

［1］Lee J，Chung M K，Cho Y G，et al.Mapping and scheduling of tasks and communica-tions on many-core soc under local memory constraint［J］.IEEE Trans.on Computer-aided Design of integrated circuits and System，2013，32（11）：1748－1761.

［2］Venugopalan S，Sinnen O.ILP formulations for optimal task scheduling with communi-cation delays on parallel systems［J］.IEEE Trans.on Parallel and Distributed Systems，2014，（99）：1－10.

［3］Topcuoglu H，Hariri S，Wu M Y.Performance-effective and low-complexity task scheduling for heterogeneous compu-ting［J］.IEEE Trans.on Parallel and Distributed Systems，2002，13（3）：260－274.

［4］Fan M，Quan G.Harmonic-aware multi-core scheduling for fixedpriority real-time systems［J］.IEEE Trans.on Parallel and Distributed Systems，2014，25（6）：1476－1488.

［5］Lan Z，Sun S X.Task scheduling genetic algorithm based on the knowledge of critical path［J］.Computer Applications，2008，28（2）：272－274.（兰舟，孙世新.基于关键路径知识的任务调度遗传算法［J］.计算机应用，2008，28（2）：272－274.）

［6］Chopra N，Singh S.HEFT based workflow scheduling algorithm for cost optimization within deadline in hybrid clouds［C］∥Proc.of the 4th International Conference on Computing，Communications and Networking Technologies，2013：1－6.

［7］TabakE K，Cambazoglu B B，Aykanat C.Improving the performance of independent task assignment heuristics minmin，maxmin and sufferage［J］.IEEE Trans.on Parallel and Distributed Systems，2014，25（5）：1244－1256.

［8］Omara F A，Arafa M M.Genetic algorithms for task scheduling problem［J］.Journal of Parallel and Distributed Computing，2010，70（1）：13－22.

［9］Wen Y，Xu H，Yang J D.A hybrid heuristic-genetic algorithm for task scheduling in heterogeneous processor networks［J］.Journal of Parallel and Distributed Computing，2011，71（11）：1518－1531.

［10］Zhou S E，Lei H.Based on the improved genetic-simulated annealing algorithm for task scheduling orderly［J］.Micro-electronics and Computer，2006，23（10）：62－64.（周双娥，雷辉.基于改进的遗传－模拟退火的有序任务调度算法［J］.微电子学与计算机，2006，23（10）：62－64.）

［11］Li J M，Zhang B，Wang X.Heterogeneous multiprocessor task scheduling based on particle swarm optimization algorithm［J］.Application Research of Computers，2012，29（10）：3621－3624.（李静梅，张博，王雪.基于粒子群优化的异构多处理器任务调度算法［J］.计算机应用研究，2012，29（10）：3621－3624.）

［12］Faragardi H R，Shojaee R，Yazdani N.Reliability-aware task allocation in distributed computing systems using hybrid simu-lated annealing and tabu search［C］∥Proc.of the 14th IEEE International Conference on High Performance Computing and Communication ＆IEEE9th International Conference on Embedded Software and Systems，2012：1088－1095.

［13］Hou E，Ansari N，Ren H.A genetic algorithm for multiprocessor scheduling［J］.IEEE Trans.on Parallel and Distributed Systems，1994，5（2）：113－120.

［14］Peng M M，Huang L.Task scheduling and load balancing for multi-processors［J］.Microelectronics and Computer，2011，28（11）：35－39.（彭蔓蔓，黄亮.多核处理器中任务调度与负载均衡的研究［J］.微电子学与计算机，2011，28（11）：35－39.）

［15］Hwang R，Gen M，Katayama H.A comparison of multiprocessor task schedu-ling algorithms with communication costs［J］.Computers and Operations Research，2008，35（3）：976－993.

［16］Zhong Q X，Xie T，Chen H W.Task matching and scheduling by genetic algorithm［J］.Journal of Computer Rese-arch and Development，2000，37（10）：1197－1203.（钟求喜，谢涛，陈火旺.基于遗传算法的任务分配与调度［J］.计算机研究与发展，2000，37（10）：1197－1203.）

［17］Yuan X L，Zhong M Y.Improved genetic algorithms for parallel task scheduling［J］.Computer Engineering and Applications，2011，47（10）：56－59.（袁雪莉，钟明洋.改进遗传算法的并行任务调度［J］.计算机工程与应用，2011，47（10）：56－59.）

Modified hybrid genetic algorithm for parallel task scheduling of multiprocessors

YAO Ying-biao，WANG Xuan
（College of Communication Engineering，Hangzhou Dianzi University，Hangzhou 310018，China）

Parallel task scheduling of multiprocessors is a hot research topic，and also is a well known NP-hard problem.Focusing on this problem，a modified hybrid genetic algorithm（MHGA）is proposed，in which the heuristic algorithm，tabu search（TS）algorithm and simulated annealing（SA）algorithm are integrated.The modifications of the MHGA include：using the hierarchical scheduling based heuristic method to initialize the population so as to improve the quality of initial population；employing the TS based random number crossover to enhance the diversity of the population；adopting the SA based mutation to improve the quality of the individual.Experimental results show that the MHGA can obtain smaller task scheduling time and have ability to fast search better solution in comparison with other GAs.

genetic algorithm（GA）；tabu search（TS）；simulated annealing（SA）；parallel scheduling；multiprocessor

TP 332

A

10.3969／j.issn.1001-506X.2015.08.32

姚英彪（1976－），男，副教授，博士，主要研究方向为计算机体系结构、嵌入式系统设计。

E-mail：yaoyb＠hdu.edu.cn

王 璇（1991－），女，硕士研究生，主要研究方向为多核处理器任务调度。

E-mail：15158116166＠163.com

1001－506X201508－1928－08

网址：www.sys－ele.com

2014－09－11；

2014－10－30；网络优先出版日期：2015－01－20。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150120.1050.006.html

国家自然科学基金（61100044），中国浙江省科技厅科技计划项目（2013C31100）资助课题