基于自适应ε的约束优化算法

2015-05-25毕晓君

系统工程与电子技术 2015年8期

关键词：测试函数约束条件全局

毕晓君，张磊

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

基于自适应ε的约束优化算法

毕晓君，张磊

（哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001）

针对目前约束优化算法易陷入局部最优和鲁棒性不好等缺点，提出基于自适应ε的约束优化算法。首先，通过改进的个体比较准则，充分利用优秀不可行个体的有效信息，加大对搜索空间的探索力度，从而提高种群多样性；其次，提出自适应ε调整策略，平衡目标函数和约束违反度之间的关系，进而更加合理地进行个体比较。对13个标准测试函数的对比实验表明，本文算法不仅能够以较高精度收敛到全局最优解，而且鲁棒性较好。

约束优化算法；个体比较准则；ε约束；自适应

0 引言

约束优化问题是一类广泛存在于现实世界中但又较难求解的问题，涉及到函数优化［1］、图像处理［2］、网络通信［3］等诸多领域，对其研究具有重要的理论和实际意义。目前，一般采用约束优化算法处理约束优化问题，而有效的约束优化算法必须在处理约束条件的同时能够收敛到全局最优解。

传统的全局优化算法如遗传算法［4］、粒子群算法［5］、差分进化算法［6－7］、免疫克隆算法［8］等必须结合约束处理技术才能处理约束优化问题。约束处理技术作为约束优化算法中非常重要的组成部分，常用方法有惩罚函数法［9］、Deb准则［10］、随机排序法［11］、多目标法［12］和ε约束［13］等。研究表明，基于ε约束的优化算法在处理约束优化问题上取得良好的效果，但在收敛精度和鲁棒性上仍需进一步提高。文献［14］提出一种基于分解的ε约束优化算法，该算法通过带权系数的切比雪夫计算适应度值，利用ε约束选择个体，但是该算法的鲁棒性不好。文献［15］提出一种基于偏好的ε约束优化算法，该算法通过引入偏好信息减少计算量，但易陷入局部最优。文献［16］提出一种ε约束生物地理学优化算法，该算法有效地提高了收敛速度和精度，但缺乏与ε约束优化算法的实验对比。文献［17］提出一种基于排序的ε约束差分进化算法，该算法有效减少了适应度评价次数，但是收敛精度较低。文献［18］提出一种εDE算法，但是该算法的收敛精度不高，并且适应度评价次数很多。由于约束优化问题存在各种复杂约束条件（线性、非线性、不等式、等式），可行域与不可行域的拓扑结构变得很复杂，使得算法兼顾多样性和收敛性的难度很大，特别是对于等式约束条件较多和决策变量维数较高的约束优化问题，需要进一步提高对搜索空间的探索和开发能力，才能更好地协调种群的多样性和收敛性。因此，急需研究开发更为有效的方法进行个体评价与比较，在保持多样性的同时，能够引导算法搜索满足约束条件的全局最优解。

针对上述问题，本文提出一种个体比较准则和自适应ε参数调整策略，构成基于自适应ε的约束优化算法（selfadaptiveεconstrained optimization algorithm，εCOA）。改进的个体比较准则能够充分利用优秀不可行个体信息，加大对搜索区域的探索能力，避免陷入局部最优；同时，采用自适应ε参数调整策略，更好地平衡可行个体和不可行个体的关系，进一步提高算法的搜索效率和鲁棒性。

1 约束优化问题描述及相关定义

不失一般性，以最小化问题为例，约束优化问题如式（1）所示。

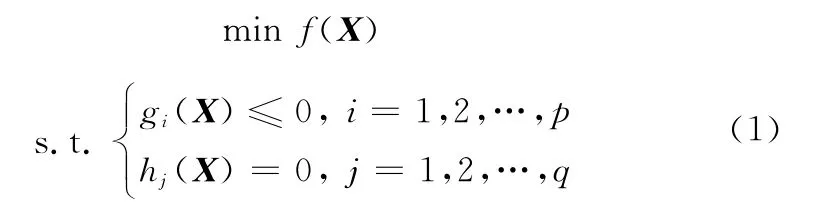
式中，X＝（x1，x2，…，xn）∈Rn是n维决策变量，每一维xi∈［li，ui］，i＝1，2，…，n；f（X）是目标函数；gi（X）是第i个不等式约束条件；p是不等式约束条件个数；hj（X）是第j个等式约束条件；q是等式约束条件个数。与其他文献一样，本文将等式约束条件转化为不等式约束条件［19］，具体如式（2）所示。

式中，δ是很小的实数，本文参考文献［19］取值为0.000 1。

将满足所有约束条件的个体空间S称为式（1）的可行域，否则称为不可行域，S⊆Rn。包括在S中的个体X称为可行个体，否则称为不可行个体。

约束违反函数如式（3）所示，其大小称为约束违反度。

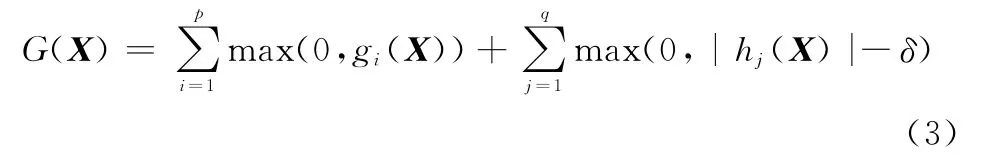
2 相关文献回顾

Deb准则［10］是一种有效的个体比较机制，因其操作简单和无需设置参数受到很大的关注，它由3条准则构成：

（1）两个都是可行个体，目标函数小的获胜；

（2）两个都是不可行个体，约束违反度小的获胜；

（3）一个是可行个体，另一个是不可行个体，可行个体获胜。

但是，Deb准则存在一个明显缺陷，它强调可行个体一定优于不可行个体，导致种群容易陷入早熟收敛。

文献［18］在Deb准则基础上提出一种改进的个体比较准则，在一定程度上利用了不可行个体，主要由3条准则组成：

（1）两个都是可行个体，目标函数小的获胜；

（2）两个都是不可行个体，约束违反度小的获胜；

（3）一个是可行个体，另一个是不可行个体：如果不可行个体的约束违反度小于等于ε，目标函数小的获胜；如果不可行个体的约束违反度大于ε，可行个体获胜。

其中，对于ε设置如下：

式中，gen为进化代数；ε（0）＝1。

但是，该方法对于一些复杂的约束优化问题仍存在收敛精度不高的问题，归其原因还是由于对搜索空间的探索利用能力不足和参数调整的缺陷，导致种群多样性下降。

3 基于自适应ε的约束差分进化算法

通过深入研究分析，本文算法从个体比较准则、ε设置两个方面进行改进，综合提高全局搜索能力。首先，改进的个体比较准则不只是基于约束违反度来比较不可行个体，而是较好地兼顾目标函数和约束违反度，使得进化朝着全局最优方向进行。其次，为了进一步提高算法鲁棒性，设计新的自适应ε参数调整策略，进而有效合理地比较个体。

3.1 改进的个体比较准则

对于约束优化问题，其中最为关键的就是要通过有效的方法在可行个体之间、不可行个体之间以及可行个体与不可行个体之间进行评价与比较，从而引导算法搜索满足约束条件的全局最优解。不可行个体在进化中对维持种群多样性起着非常重要的作用，但目前的方法对于不可行个体利用不足，导致算法容易陷入局部最优。为了充分利用优秀不可行个体的有效信息，加强对搜索区域的探索能力，保持进化种群的多样性，本文提出一种改进的个体比较准则，具体形式为：

准则1 两个都是可行个体，目标函数值小的个体获胜。

准则2 一个是可行个体，另一个是不可行个体，分两种情形进行讨论：（情形1）不可行个体的约束违反度小于等于ε，基于目标函数值比较，目标函数值小的个体获胜；（情形2）不可行个体的约束违反度大于ε，可行个体获胜。

准则3 两个都是不可行个体时，分3种情形进行讨论：（情形1）两个个体的约束违反度都小于等于ε，目标函数值小的个体获胜；（情形2）一个个体的约束违反度小于等于ε，另一个体的约束违反度大于ε，约束违反度小的个体获胜；（情形3）两个个体的约束违反度都大于ε，以较大概率Ps基于约束违反度比较，约束违反度小的个体获胜，以较小概率1－Ps基于目标函数值比较，目标函数值小的个体获胜。

上述个体比较准则可以转化为如式（5）所示形式。

对于准则1：目标函数较优个体进入下一代种群，有利于保证种群向更优可行方向进化。对于准则2：保留约束违反度小、目标函数值小的优秀不可行个体，有利于加大对搜索空间的探索范围，从而提高种群多样性。对于准则3：实际中有很多复杂约束优化问题，其可行域十分狭小，种群进化中会产生很多不可行个体，所以大多数情况都是不可行个体之间的比较。情形1、情形2能够保留约束违反度和目标函数同时较优的不可行个体，更大程度地保留了不可行个体的有效信息，进而能够更好地向全局最优方向收敛。情形3以较小概率1－Ps基于目标函数比较个体，从而保留极少数约束违反度较大的个体，这样可以进一步加强对搜索空间的探索。同时这些不可行个体只会存在于极少数的进化代数中，而不会影响整体的进化过程。

上述准则为什么能够收敛到全局最优解？首先，准则1中可行个体利用目标函数比较，可以让进化在可行域内朝着更优可行方向进行；其次，准则2、准则3保证种群中存在一定的优秀不可行个体，不仅有利于加强种群多样性，而且进化从不可行域向可行域进行。所以改进的个体比较准则可以让种群在可行域和不可行域同时向全局最优方向进化，从而保证收敛性。

3.2 ε水平设置

从式（4）给出的ε参数设置方法可以看出，ε随着进化代数的增加呈等比例减少，并且只单纯地依赖进化代数，忽略了种群的整体信息，这样将直接导致ε对个体选择的压力不准确，不能很好地平衡目标函数和约束违反度的关系。当进化初期不可行个体较多时，ε过大使得往往只是基于目标函数比较个体，导致较多进化代数后种群很难到达可行域，甚至可能停滞在不可行域；而ε过小将导致不能很好利用优秀不可行个体，目标函数较优而约束违反度较小的不可行个体无法得到保留，势必会影响种群的多样性。同时，ε的初始设置取常数1将直接影响不能有效处理不同问题，并对进化过程产生不利影响。因此，单纯依据进化代数来调整ε还存在较大的缺陷，每一代的ε应当根据种群的整体约束违反度，针对不同问题可行域的变化，进行自适应调整。在可行域较小时产生相对较大的ε，从而扩大搜索区域，增大跳出局部最优的可能；反之，产生较小ε，增强种群开发能力，加快种群收敛速度。基于上述思想，本文提出如式（6）、式（7）所示的ε自适应调整策略。

式中，Te为截断进化迭代次数，用于控制ε（t）的大小。Te不宜过大也不宜过小，过大时将会使得在进化后期种群中还存在很多不可行个体，这势必会影响种群最终收敛到全局可行解；而过小时，第3.1节中的个体比较准则将会非常近似于Deb准则，从而使得在进化前期就排除了大量不可行个体，出现类似Deb准则容易陷入局部最优的缺点。α＝αmin＋λ×（αmax－αmin）；N为种群大小；λ＝Num（feasible）／N，λ表示种群中可行个体在整个种群中的比例。在进化过程中不再单纯依靠进化代数，而是利用整个种群的约束违反度设置初始ε。同时根据可行个体所占比例，对ε进行自适应调整，有效平衡个体的目标函数和约束违反度，提高算法搜索效率。

3.3 本文算法流程

εCOA采用差分进化算法［17］作为进化机制，主要流程如下：

步骤1 初始化。设置初始参数包括种群规模N、缩放因子F、交叉因子CR、最大迭代次数Gmax。利用随机方法初始化种群，每个个体Xi＝（x1，x2，…，xn）的第j维分量xj＝lj＋rand（）×uj（j＝1，2，…，n；i＝1，2，…，N）。其中，rand为［0，1］的随机数；xj∈［lj，uj］。

步骤2 判断终止条件。如果达到最大迭代次数Gmax，算法结束；否则，转到步骤3。

步骤3 变异操作。按式Vi（t＋1）＝Xr1（t）＋F×（Xr2（t）－Xr3（t））进行变异操作。其中，t为进化代数；i，r1，r2，r3为1～N上互不相等的正整数。

步骤4 交叉操作。按

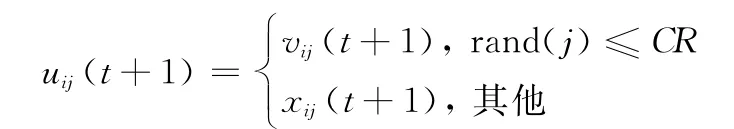
进行交叉操作。其中，t为进化代数；vij为个体Vi的第j维分量；xij为个体Xi的第j维分量；rand（j）为［0，1］的随机数。

步骤5 选择操作。按第3.1节方法比较个体。

步骤6 按式（6）、式（7）更新ε（t）。

步骤7 t＝t＋1，返回到步骤2。

4 实验及分析

本文所有实验在硬件配置为Intel Pentium，CPU：G620、4GB内存、主频2.6GHz的计算机上进行，程序采用Matlab R2010编写。

为了验证本文算法的有效性和先进性，采用文献［19］中的13个国际通用测试函数（g01～g13）进行测试。在有效性方面与文献［18］进行了对比实验，在先进性方面，与目前先进的ISR算法［11］、εRDE算法［17］、SMES算法［20］进行了对比实验。

本文算法的参数均通过大量实验和一定的经验得出。其中对于取值N＝50、F＝0.7、CR＝0.8（参考文献［13］），取值Gmax＝10 000（参考文献［18］），Ps为（0.9 1.0）上的随机数，αmin＝3.5，αmax＝9.5。而对于关键参数取值Te＝1 000则是通过实验得出，具体讨论见第4.3节。

4.1 有效性验证

为了验证εCOA的有效性，与文献［18］进行了对比实验，测试项目包括最优值、最差值、平均值及标准差。对于每个测试函数在相同条件下算法均独立运行50次，仿真实验结果如表1所示。εCOA的最大评价次数为500 000，εDE的最大评价次数为2 000 000。

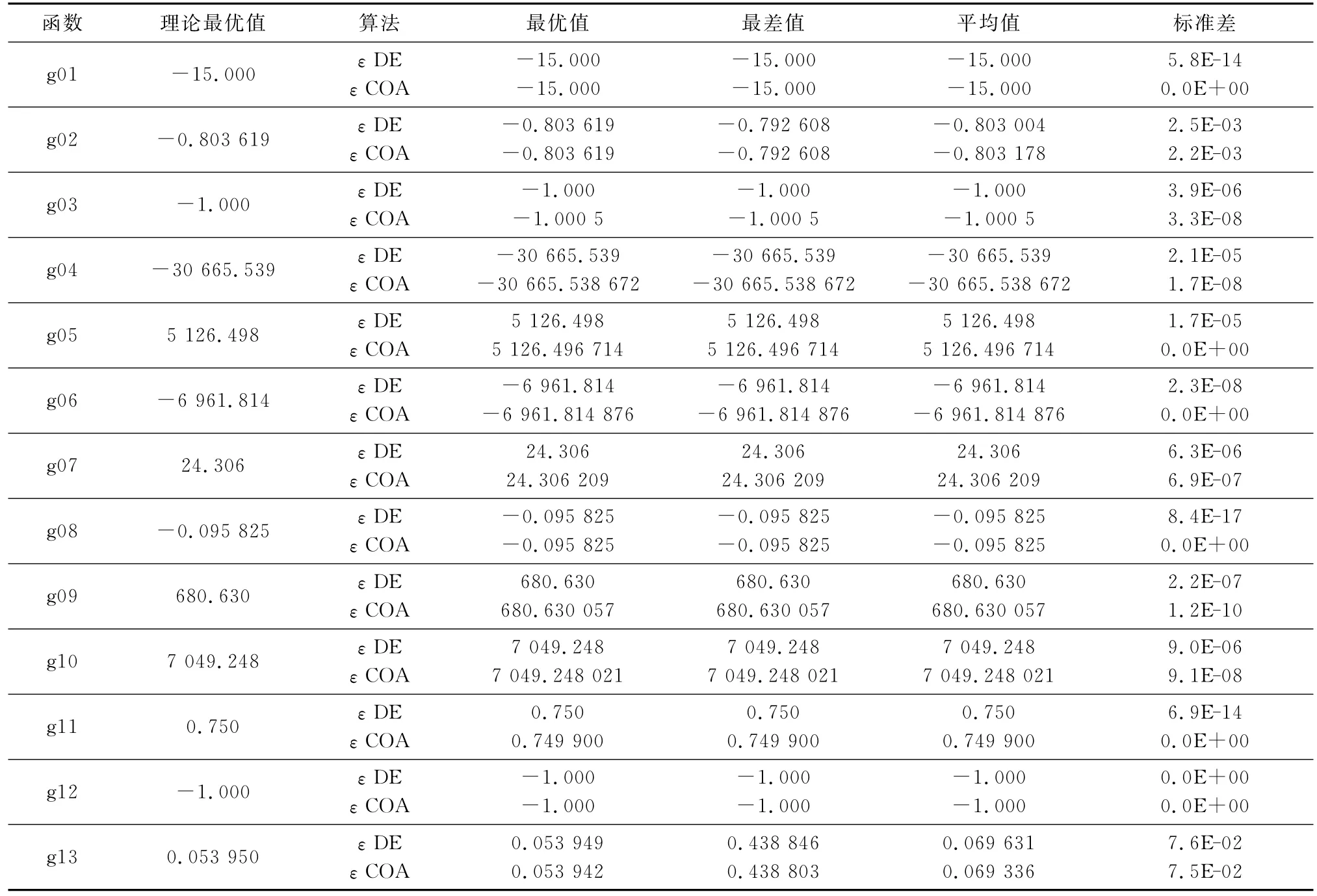
表1 εCOA与εDE对比实验结果

由表1可以看出，εCOA较εDE具有明显的优势。εCOA和εDE在11个测试函数（g02、g13除外）都一致达到全局最优解，但εCOA的标准差几乎均优于εDE，说明εCOA的收敛精度更高；同时，在函数g02上，εCOA较εDE的平均值和标准差都更小，说明εCOA收敛精度更高，鲁棒性也更好；在函数g13上，εCOA较εDE平均值更小，标准差相当；并且εCOA最大评价次数只有εDE的25%，说明εCOA在运行时间具有很大的优势。从以上分析可以得出，εCOA较εDE具有更好的约束优化性能。

4.2 先进性验证

为了进一步验证εCOA的先进性，将εCOA与ISR算法［11］、εRDE［17］算法以及SMES算法［20］进行了对比实验，对每个测试函数在相同条件下独立运行50次，仿真实验结果如表2所示。

从表2可以看出，εCOA在11个测试函数（g02、g13除外）50次独立运行时一致达到全局最优解；ISR只在9个测试函数（g02、g07、g10、g13除外）上一致达到全局最优解，ISR在g13上的均值和标准差略优于εCOA，由于相差较小并且独立运行次数只有30次，所以ISR和εCOA在处理g13时能力相当，而在g02、g07、g10上，εCOA的最差值、平均值和标准差均优于ISR，说明εCOA具有更高的收敛精度和更好的鲁棒性；SMES只在7个测试函数上一致达到全局最优解（g02、g05、g06、g07、g09、g13除外），εCOA几乎在所有测试函数上的性能均优于SMES；εRDE在11个测试函数上一致达到了全局最优解（g02、g07除外），εRDE在g13上的均值和标准差优于εCOA，也是4种算法中唯一一致达到全局最优解的，但是独立运行次数只有30次，而在g03、g07、g10上εCOA的最差值和标准差都更优，说明εCOA具有更好的鲁棒性。从以上分析可以得出，εCOA在处理13个基本测试函数时具有一定的优势。

g02决策变量的维数较高，搜索空间的拓扑结构十分复杂，使得对其求解难度很大，5种算法都未一致达到全局最优解。g13等式约束条件较多，从而可行域空间十分狭小，大多数算法未一致达到全局最优解。可以看出对于决策变量维数较高、等式约束条件较多的问题，大多数算法都存在一定的缺陷，需要进一步改善算法的探索和开发能力，更好兼顾种群的多样性和收敛性。

表2 εCOA与其他3种算法的比较结果

4.3 参数Te的分析

在εCOA中，最重要的参数是截断进化迭代次数Te。为了分析不同的Te取值对εCOA收敛性能的影响，通过对不含等式约束条件的函数g01和含有复杂等式约束条件的函数g03、g11和g13进行实验，独立运行次数为5次，实验结果如图1～图4所示。

图1 在g01上不同Te取值下的最优值均值

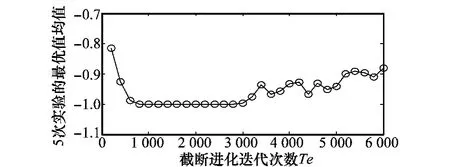
图2 在g03上不同Te取值下的最优值均值

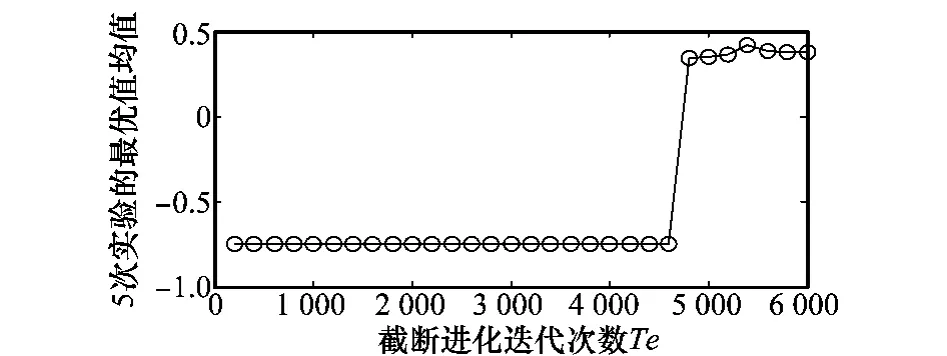
图3 在g11上不同Te取值下的最优值均值

图4 在g13上不同Te取值下的最优值均值

从图1可以看出，对于只含有不等式约束条件的函数g01，当Te的取值范围从200代到4 000代左右时，εCOA在5次独立运行实验中都能达到全局最优解，而从4 000代之后，εCOA不能一致收敛到全局最优解；从图2可以看出，当Te的取值范围从800到3 000代左右时，εCOA在5次独立运行实验中都能一致收敛到全局最优解，而在3 000代之后不能一致收敛；从图3可以看出，在Te取值4 600代左右后出现不能一致收敛的情况；从图4可以看出，当Te的取值范围从800代到4 600代左右时，εCOA在5次独立实验中达到一致收敛；而在5 000代之后，出现了种群中甚至没有可行个体的情况，所以在图4中没有最优值均值。以上实验结果表明，当Te的取值过小时（小于800代），由于对不可行个体的有效信息利用不足，对于等式约束条件较多进而可行域很小的函数，算法不能一致收敛到全局最优解；而当Te的取值过大时（大于4 600代），由于过多的利用不可行个体，使得算法对可行域搜索力度不够，从而不能充分收敛到全局最优解，甚至不能进入可行域。基于上述实验结果和分析，Te取值800～3 000较为合适，而在所有测试函数上统一取值1 000。

5 结束语

本文在深入研究约束优化问题的基础上，提出一种自适应ε约束优化算法。首先通过改进约束处理技术，充分利用不可行个体的有效信息，加强算法的探索能力，增强多样性，避免陷入局部最优；其次通过自适应设置ε，平衡可行个体与不可行个体的关系，提高算法的鲁棒性和搜索效率。仿真实验结果表明，εCOA不仅能够收敛到全局最优解，而且鲁棒性较好。但是对于决策变量维数较高、等式约束条件较多的复杂约束优化问题，仍需要进一步提高种群的多样性和收敛性，使之一致收敛到全局最优解。

［1］Bi X J，Wang Y J.Artificial bee colony algorithm with fast convergence［J］.Systems Engineering and Electronics，2011，33（12）：2755－2761.（毕晓君，王艳娇.加速收敛的人工蜂群算法［J］.系统工程与电子技术，2011，33（12）：2755－2761.）

［2］Kang L，Wu L，Chen X，et al.Practical structure and motion recovery from two uncalibrated images usingεconstrained adaptive differential evolution［J］.Pattern Recognition，2013，46（5）：1466－1484.

［3］Du X Y，Sun L J，Guo J，et al.Coverage optimization algorithm for heterogeneous WSNs［J］.Journal of Electronics ＆Information Technology，2014，36（3）：697－701.（杜晓玉，孙力娟，郭剑，等.异构无线传感器网络覆盖优化算法［J］.电子与信息学报，2014，36（3）：697－701.）

［4］Wu T Y，Xu J H，Liu J Y，et al.Improved genetic algorithm for vehicle routing problem with hard time windows［J］.Systems Engineering and Electronics，2014，36（4）：708－713.（吴天羿，许继恒，刘建永，等.求解有硬时间窗车辆路径问题的改进遗传算法［J］.系统工程与电子技术，2014，36（4）：708－713.）

［5］Yan Z C，Luo Y S.A particle swarm optimization algorithm based on simulated annealing［C］∥Proc.of the Conference on Advanced Materials Research，2014：2301－2305.

［6］Elsayed S M，Sarker R A，Essam D L.An improved self-adaptive differential evolution algorithm for optimization problems［J］.IEEE Trans.on Industrial Informatics，2013，9（1）：89－99.

［7］Wisittipanich W，Kachitvichyanukul V.Mutation strategies toward Pareto front for multi-objective differential evolution algorithm［J］.International Journal of Operational Research，2014，19（3）：315－337.

［8］Gou S，Zhuang X，Li Y，et al.Multi-elitist immune clonal quantum clustering algorithm［J］.Neurocomputing，2013，101（2）：275－289.

［9］Datta R，Deb K.Individual penalty based constraint handling using a hybrid bi-objective and penalty function approach［C］∥Proc.of the IEEE Congress on Evolutionary Computation，2013：2720－2727.

［10］Mezura-Montes E，Coello C A.Constraint handling in nature-inspired numerical optimization：past，present and future［J］.Swarm and Evolutionary Computation，2011，1（4）：173－194.

［11］Runarsson T P，Yao X.Search biases in constrained evolutionary optimization［J］.IEEE Trans.on Systems Man and Cybernetics-Part C：Applications and Reviews，2005，35（2）：233－243.

［12］Long Q.A constraint handling technique for constrained multiobjective genetic algorithm［J］.Swarm and Evolutionary Computation，2014，15（4）：66－79.

［13］Takahama T，Sakai S.Constrained optimization by theεconstrained differential evolution with gradient-based mutation and feasible elites［C］∥Proc.of the IEEE Congress on Evolutionary Computation，2006：1－8.

［14］Asafuddoula M，Ray T，Sarker R.An adaptive constraint handling approach embedded MOEA／D［C］∥Proc.of the IEEE Congress on Evolutionary Computation，2012：1－8.

［15］Landa R，Coello C A C，Toscano-Pulido G.Goal-constraint：incorporating preference through an evolutionaryε-constraint based method［C］∥Proc.of the IEEE Congress on Evolutionary Computation，2013：741－747.

［16］Bi X J，Wang J，Li B，et al.Anεconstrained biogeographybased optimization with dynamic migration［J］.Journal of Computer Research and Development，2014，51（3）：580－589.（毕晓君，王珏，李博，等.基于动态迁移的ε约束生物地理学优化算法［J］.计算机研究与发展，2014，51（3）：580－589.）

［17］Tetsuyuki T，Setsuko S.Efficient constrained optimization by theεconstrained rank-based differential evolution［C］∥Proc.of the IEEE Congress on Evolutionary Computation，2012：10－15.

［18］Zheng J G，Wang X，Liu R H.ε-Differential evolution algorithm for constrained optimization problems［J］.Journal of Software，2012，23（9）：2374－2387.（郑建国，王翔，刘荣辉.求解约束优化问题εDE算法［J］.软件学报，2012，23（9）：2374－2387.）

［19］Wang Y，Cai Z X.Combining multi-objective optimization with differential evolution to solve constrained optimization problems［J］.Evolutionary Computation，2012，16（1）：117－134.

［20］Mezura-Montes E，Coello C A.A simple multi-membered evolution strategy to solve constrained optimization problems［J］.IEEE Trans.on Evolutionary Computation，2005，9（1）：1－17.

Self-adaptiveεconstrained optimization algorithm

BI Xiao-jun，ZHANG Lei
（Institute of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China）

Since current constrained optimization algorithms are easy to fall into the local optimum and their robustness are weak，a self-adaptiveεconstrained optimization algorithm is proposed.By improving the individual comparison criterion，it can make full use of effective information carried by the infeasible solution，then enhance the exploration in the search space and improve the population diversity.Simultaneously，a self-adaptive adjustment strategy is presented to produce a suitableεfor balancing the relationship between the objective function and the constraint violation degree according to different problems，which can make more reasonable comparisons between individuals.Finally，comparative experiments on thirteen benchmark functions show that the proposed algorithm is not only able to converge the global optimal solution with higher accuracy but also has better robustness.

constrained optimization algorithm；individual comparison criteria；εconstrained；self-adaptive

TP 18

10.3969／j.issn.1001-506X.2015.08.29

毕晓君（1964－），女，教授，博士，主要研究方向为信息智能处理技术、智能优化算法、数字图像处理。

E-mail：bixiaojun＠hrbeu.edu.cn

张磊（1987－），男，博士研究生，主要研究方向为信息智能处理技术、约束多目标优化。

E-mail：zl12306124＠163.com

1001－506X201508－1909－07

网址：www.sys－ele.com

2014－07－11；

2014－11－14；网络优先出版日期：2015－03－23。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150323.1706.004.html