支持向量回归机预测误差校正方法

2015-05-25彭小奇唐秀明宋彦坡

系统工程与电子技术 2015年8期

陈君，彭小奇，唐秀明，宋彦坡，刘征

（1.中南大学信息科学与工程学院，湖南长沙410083；2.湖南第一师范学院信息科学与工程系，湖南长沙410205；3.湖南科技大学信息与电气工程学院，湖南湘潭411201）

支持向量回归机预测误差校正方法

陈君1，3，彭小奇1，2，唐秀明3，宋彦坡1，刘征1

针对传统的ε-不敏感支持向量回归机（ε-insensitive support vector regression，ε-SVR）未充分考虑局部支持向量对回归预测结果的影响，不利于提高回归预测精度的问题，提出了一种ε-SVR预测误差校正方法。该方法以期望预测值与ε-SVR回归预测值及局部支持向量间的欧氏距离和最小为目标函数，以ε不敏感损失带（ε-tube）宽度为约束条件，通过利用高维特征空间中ε-tube边界上和边界外的局部支持向量对ε-SVR的回归预测值进行误差校正。利用人工产生的不同分布数据集和UCI数据集进行的仿真结果表明，与传统的ε-SVR相比，该文方法具有更高的预测精度和更强的泛化能力。

支持向量回归机；误差校正；预测精度；泛化能力

0 引言

Cortes和Vapnik基于VC维理论和结构风险最小化原则于20世纪90年代提出的支持向量机［1］，因具有稀疏性、全局优化、泛化能力强等优点而得到广泛研究与应用［2－4］，其中的ε-不敏感支持向量回归机（ε-insensitive support vector regression，ε-SVR）主要用于时间序列观测和过程控制、优化等［5－7］。传统的ε-SVR在高维特征空间所寻找的ε-tube宽度固定、结构对称［1］，而实际的数据样本分布不可避免地存在不等性方差或呈现出某种局部变化趋势，导致ε-SVR的输出出现程度不等的误差。同时，求取ε－SVR前所确定的ε值在训练过程中是固定不变的，其取值主要根据经验来确定：当ε增大时，相应的解呈现出稀疏性，回归曲线更加平滑；当ε减小时，更多的样本成为支持向量（support vector，SV），可能产生过拟合现象；若采用交叉验证法来确定ε值，则其计算复杂性和计算成本将显著增加。为此，文献［8］提出了一种通过引入参数ν来控制支持向量数目和训练误差的支持向量机ν-SVR，当处理带有不等性方差的数据样本时，ν-SVR通过假设ε-SVR中存在一个变形ε-tube并使用随机参数模型估计ε带的宽度，但该文献未指出如何得到。文献［9］提出把ε-tube分成上边界和下边界两个部分，通过对样本数据的分布进行估计来确定上、下边界，但这种估计需要额外的估计算法。文献［10］针对样本分布的局部变化趋势，提出了一种边界自适应的局部化SVR，因其要对每个训练样本进行处理而增加了计算的时间复杂性。文献［11］提出在ε-SVR的基础上分别给出参数化的上、下边界函数，但边界函数的求解难度较大，文献［12］在ε-SVR框架下考虑样本之间的相关性和样本密度，提出解决小样本初始训练数据的多标准主动学习方法的SVR。文献［13－15］提出的孪生支持向量回归机（twin support vector regression，TSVR）把ε-SVR问题转化为求上、下边界超平面函数的两个优化问题，但其解不具有稀疏性。文献［16］提出同时求解函数和其微分的TSVR方法，以改善TSVR的估计精度和运算时间的复杂性。

以上文献主要从ε-不敏感损失函数（ε-insensitive loss function，ε-ILF）和ε-tube边界两个角度对样本数据分布进行估计，希望通过调整ε-tube边界来体现样本数据的分布特性，却使ε-SVR的优化问题变得更复杂更难理解。特别是将非线性引入核函数后，因核参数的不同所引起的高维特征空间数据分布难以估计，使上述方法的应用存在较大难度。为此，本文提出一种利用局部SV对传统的ε-SVR的预测结果进行误差校正的方法，该方法以校正向量到全局预测向量和局部支持向量的欧氏距离和最小为目标函数，ε-tube宽度为约束，对全局支持向量机的输出进行误差校正。仿真结果表明，本文方法在保持传统的ε-SVR原有优越特性的同时，可有效减少预测误差，提高其泛化性能。

1 ε-SVR特性分析

1.1 ε-SVR简述

设按某个未知概率分布P（x，y）构成的训练集T＝｛（x1，y1），…，（xl，yl）｝∈（X×Y），输入矢量xi∈X＝Rn，输出yi∈Y＝R（i＝1，2，…，l），l为样本数。在函数类集合F中，寻求一个最优化决策函数f（x）＝（wx）＋b，其中，w∈Rn为权向量，b∈R为阈值。根据结构风险最小化原则，应使期望风险R［f（x）］＝∫c（x，y，f（x））dP（x，y）为极小，其中，c（x，y，f（x））是图1所示的ε-不敏感损失函数：

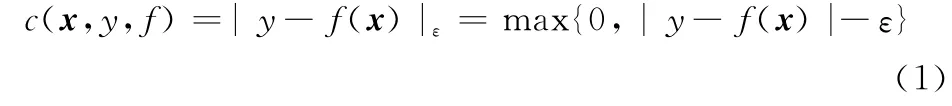
ε是预先选定的一个正数。当xi点的观测值yi与回归函数f（x）的预测值f（xi）之差不超过ε时，则认为在xi点的预测值f（xi）是无损失的。从图1可见，ε-不敏感损失函数具有宽度ε固定和结构对称性，因此，传统的ε-SVR不能很好地描述存在不等性方差或局部变化趋势的数据样本集。

图1 ε-不敏感损失函数

对于非线性回归问题，引入一个映射函数φ（x）将低维空间Rn中的非线性输入样本xi映射到线性可分的高维特征空间φ（xi）中，在此特征空间中建立相应的线性回归模型来进行输出预测。

非线性ε-SVR原始优化问题可表示为

式中，C＞0为惩罚参数，通过控制对错分样本的惩罚程度实现错分样本数与模型复杂性之间的折衷；ξ和ξ＊为松弛变量，用于提高f（x）的预测精度。对应的Lagrange函数为

式中，αi，α＊i，ηi，η＊i为非负拉格朗日乘子。据KKT条件，其对偶最优化问题为

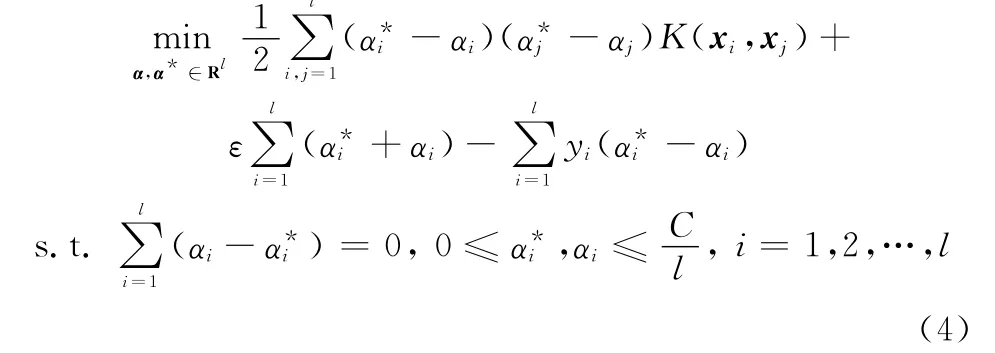
式中，K（xi，xj）＝〈φ（xi），φ（xj）〉为满足Mercer定理的核函数。求解上式得非线性回归函数：

不同时为零的αi，α＊i所对应的样本即为SV。

1.2 ε-SVR的边界特性分析

ε-SVR的ε-tube空间特性如图2、图3所示。若样本点（xi，yi）在ε-tube的内部，则ξ＊i＝ξi＝0，由式（2）给出的条件知：

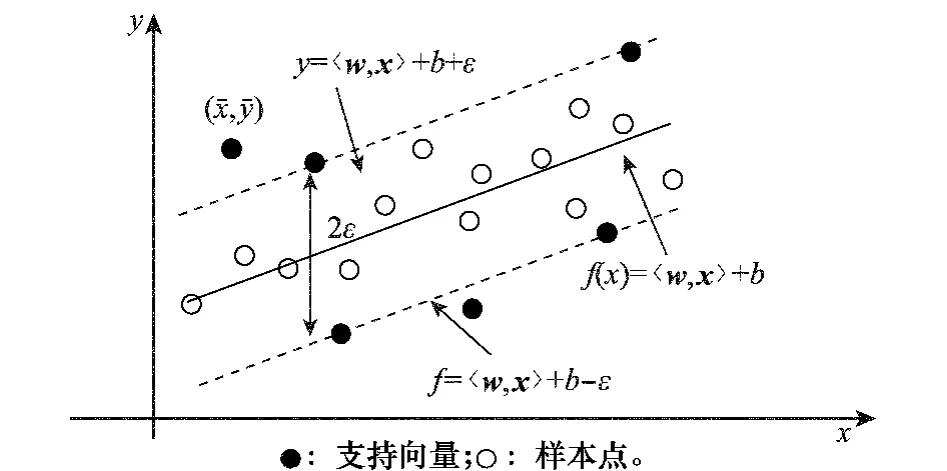
图2 单变量线性ε-tube空间特性

图3 高维线性特征空间中ε-tube的空间特性

据KKT互补条件，由式（3）可得

联解式（7）～式（10）可得α＊i＝αi＝0，即位于ε-tube内的样本点（xi，yi）对决策回归函数式（5）没有贡献。

若样本点（xi，yi）在ε-tube的边界上，则由图2、图3可知ξ＊i＝ξi＝0，当（（wφ（xi））＋b）－yi＝ε＋ξ＊i时，有ε＋ξ＊i＋yi－（wφ（xi））－b＝2ε，故由式（9）～式（11）知，此时α＊i＝0，αi∈（0，C／l）。同理，当αi＝0时，α＊i∈（0，C／l）。

若样本点（xi，yi）在ε的边界外时，ξ＊i≠0，据式（9）、式（12）有α＊i＝C／l，αi＝0。同理，当ξi≠0时，αi＝C／l，α＊i＝0。

由上述分析可知：

（1）若样本点（xi，yi）在ε-tube的内部，则α＊i＝αi＝0；

（2）若样本点（xi，yi）在ε-tube的边界上或外部，则αi，α＊i两者不同时为0。

由此可见，ε-SVR的训练误差主要由边界外的训练样本产生。单变量线性ε-SVR的ε-tube空间特性如图2所示：当样本点（xi，yi）位于两虚线之间的ε-tube内时，可认为该点没有误差；当样本点（x－，y－）位于ε-tube之外时，才有误差出现，其大小为ε－｜y－－f（x－）｜。显然，为得到预测误差小、泛化性能好的ε-SVR，需要寻找更平滑和紧致的ε-tube去拟合数据样本的分布轮廓。

2 ε-SVR的预测误差校正方法

2.1 ε-SVR的预测误差校正原理

传统的ε-SVR的ε-tube具有宽度固定和结构对称性，如图3所示。在高维线性特征空间，输入矢量xf通过决策函数式（5）可得到输出yf。根据统计模型的局部回归拟合特性［17］，在高维特征空间中的理想回归向量（φ（xf），ycf）应在ε-tube约束下，由ε-SVR所得预测向量（φ（xf），yf）向超平面γ和超平面δ所确定的区域内的局部支持向量（φ（xsv1），ysv1），（φ（xsv2），ysv2）偏移，即理想的回归向量（φ（xf），ycf）应由全局SV和（φ（xf），yf）所在区域的局部SV共同决定。

从对ε-SVR的边界特性的分析可知，在ε-tube边界外的SV是产生ε-SVR训练误差的主要原因，由此所产生的训练误差最终将影响由决策函数式（5）获得的期望预测值。距离期望预测向量越远的SV对预测值的贡献越小，距离期望预测向量越近的SV对预测值的贡献越大。为此，特征空间中一点的范式为用欧几里得距离度量SV与预测向量之间的距离：

式中，（φ（xsv），ysv）是高维特征空间中的SV，（φ（xf），yf）是高维特征空间中的预测向量。

在高维特征空间中，据文献［11］ε-tube边界外局部多SV表征了局部数据分布的趋势，采用期望预测向量到各SV点之间的欧氏距离和最小为目标函数，能使期望预测向量有效地往多SV区域移动，达到减少误差的目的。本文以（φ（xf），yf）为球心做超球，超球包含距（φ（xf），yf）最近的K个支持向量（φ（xsvi），ysvi），i＝1，2，…，k，所得特征空间中的向量关系如图4所示，由此构成局部支持向量包裹集合Ω＝｛（φ（xf），yf），（φ（xsvi），ysvi），i＝1，…，k｝。理想的预测向量（φ（xf），ycf）应位于以（φ（xf），yf）为球心、半径为ε的超球内，且到（φ（xf），yf）和局部支持向量（φ（xsvi），ysvi）的欧氏距离之和最小，即

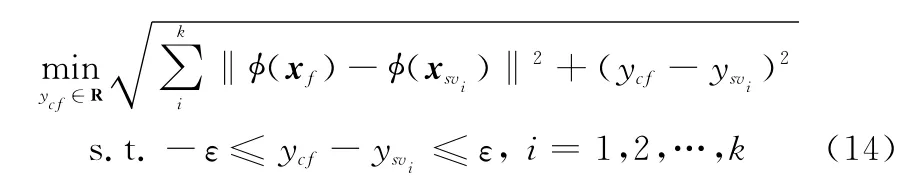
求解式（14）的约束优化问题可得经过校正后的预测值ycf。

因为映射函数φ（x）之间的距离，通过核函数K（xi，xj）＝〈φ（xi），φ（xj）〉来实现，故

图4 高维空间局部支持向量对ε-SVR预测值的影响

2.2 ε-SVR的预测误差校正步骤

ε-SVR的预测误差校正步骤如下：

步骤1 针对训练数据集T，据经验选择合适的ε-SVR的ε参数，通过交叉验证求取核参数和正则化系数C；

步骤2 利用训练样本求解式（4）所描述的优化问题，得到ε-SVR决策函数式（5）；

步骤3 找出全部SV，建立全局SV集合Ωsv；

步骤4 对输入矢量xf，由决策函数式（5）计算其预测值yf，得到高维特征空间中的非显现向量点（φ（xf），yf）；

步骤5 在高维特征空间的全局SV集合Ωsv中，对非显现向量点（φ（xf），yf）使用K近邻方法找到其K个近邻SV，构成局部SV包裹集合Ω，近邻SV到向量点（φ（xf），yf）的欧氏距离应小于等于2ε，否则应减少K值，即减少校正用局部支持向量；

步骤6 求解（14）式所描述的优化问题，得到经过误差校正后的预测值ycf。

3 实验测试与结果分析

3.1 数据描述

为比较本文方法与传统的ε-SVR的性能，构造了具有不同分布特性的两组人工数据集Data1和Data2，并从常用的UCI机器学习数据库（http：∥archive.ics.uci.edu／ml／datasets.html）中选用了5种有代表性的用于测试回归性能的数据集，数据取值全部归一化到［－1，1］之间，其具体描述如表1所示，其中训练样本从数据集随机选取，为有效的检验本文方法的泛化能力，测试样本从剩余样本中随机选取。

利用Matlab 7.11.1对本文方法进行仿真测试，所有实验均在一台Intel Core（TM）Duo 2.26GHz，2GB内存的PC机上进行，核函数选用被广泛使用，及经验证明有效的式（16）所示的高斯径向基核函数，并利用Libsvm［18］求解支持向量机。

采用均方根误差（root mean square error，RMSE）来衡量拟合效果［19］：

采用平方相关系数（squared correlation coefficient，SCC）来衡量泛化性能［20－21］。

式中，n为测试样本个数；yti表示第i个样本的目标值（观测值）；ypi表示第i个样本的预测值；和分别表示yt和 yp的平均值。

表1 标准数据集的构成特点

通过在回归问题中有代表性的测试函数sinc（x）中叠加不同的随机数来生成人工数据集（xi，yi），i＝1，…，l。sinc（x）函数定义为

式中，N（a，b）表示正态分布，a为均值，b为标准偏差；U（c，d）表示均匀分布，c为其最小值，d为其最大值。

3.2 结果分析

对表1所列数据集和人工数据集Data1和Data2，对传统的ε-SVR方法，通过交叉验证法进行参数优化后，得到在最优化核参数和正则化系数C下本文方法与传统的ε-SVR，TSVR［13］对测试样本的拟合精度和泛化性能如表2所示。在ε取值不变，即支持向量点不变的情况下，对同样的测试数据，本文方法的均方根误差均有不同程度的降低，且平方相关系数均有不同程度的提高，表明本文方法的拟合精度较高、泛化能力较强，能有效降低回归预测误差，提高ε-SVR的泛化能力。

表2 本文方法与ε-SVR、TSVR的性能比较

4 结论

本文提出了一种ε-SVR回归机预测误差校正方法。该方法以理想预测值与ε-SVR回归预测值及局部支持向量间的欧氏距离最小为目标函数，以ε-tube宽度为约束条件，通过利用高维特征空间中ε-tube边界上和边界外的局部支持向量对ε-SVR的回归预测值进行误差校正，以减小ε-SVR的预测误差，提高其预测精度及泛化能力。

仿真实验表明，与传统的ε-SVR，TSVR相比，本文方法具有更高的预测精度和更强的泛化能力。

［1］Vapnik V.The nature of statistical learning theory［M］.New York：Springer，2000.

［2］Demir B，Bruzzone L.A multiple criteria active learning method for support vector regression［J］.Pattern Recognition，2014，47（7）：2558－2567.

［3］Chen J D，Pan F.Online support vector regression-based nonlinear model predictive control［J］.Control and Decision，2014，29（3）：460－464.（陈进东，潘丰.基于在线支持向量回归的非线性模型预测控制方法［J］.控制与决策，2014，29（3）：460－464.）

［4］Song Y P，Peng X Q，Hu Z K.Meta parameters optimization method for support vector regression［J］.Systems Engineering and Electronics，2010，32（10）：2238－2242.（宋彦坡，彭小奇，胡志坤.支持向量回归机元参数优化方法［J］.系统工程与电子技术，2010，32（10）：2238－2242.）

［5］Smola A J，Schölkopf B.A tutorial on support vector regression［J］.Statistics and Computing，2004，14（3）：199－222.

［6］Wang J K，Qiao F，Li G C，et al.ε-SVR-based predictive models of energy consumption and performance for sintering［J］.Applied Mechanics and Materials，2014，548：1905－1910.

［7］LüY，Gan Z.Robustε-support vector regression［J］.Mathematical Problems in Engineering，2014，2014：1－5.

［8］Schölkopf B，Smola A J，Williamson R C，et al.New support vector algorithms［J］.Neural Computation，2000，12（5）：1207－1245.

［9］Hao P Y.New support vector algorithms with parametric insensitive margin model［J］.Neural Networks，2010，23（1）：60－73.

［10］Yang H，Huang K，King I，et al.Localized support vector regression for time series prediction［J］.Neurocomputing，2009，72（10）：2659－2669.

［11］Chen X，Yang J，Liang J.A flexible support vector machine for regression［J］.Neural Computing and Applications，2012，21（8）：2005－2013.

［12］Demir B，Bruzzone L.A multiple criteria active learning meth-od for support vector regression［J］.Pattern Recognition，2014，47（7）：2558－2567.

［13］Peng X.TSVR：an efficient twin support vector machine for regression［J］.Neural Networks，2010，23（3）：365－372.

［14］Tian Y J，Qi Z Q.Review on：twin support vector machines［J］.Annals of Data Science，2014，1（2）：253－277.

［15］Chen X，Yang J，Chen L.An improved robust and sparse twin support vector regression via linear programming［J］.Soft Computing，2014，18（12）：2335－2348.

［16］Khemchandani R，Karpatne A，Chandra S.Twin support vector regression for the simultaneous learning of a function and its derivatives［J］.International Journal of Machine Learning and Cybernetics，2013，4（1）：51－63.

［17］Amberg M，Lüthi M，Vetter T.Local regression based statistical model fitting［M］.Berlin：Springer，2010：452－461.

［18］Chang C C，Lin C J.LIBSVM：a library for support vector machines［J］.ACM Trans.on Intelligent Systems and Technology，2011，2（3）：1－27.

［19］Goyal M K，Bharti B，Quilty J，et al.Modeling of daily pan evaporation in sub tropical climates using ANN，LS-SVR，Fuzzy Logic，and ANFIS［J］.Expert Systems with Applications，2014，41（11）：5267－5276.

［20］Ni Y Q，Hua X G，Fan K Q，et al.Correlating modal properties with temperature using long-term monitoring data and support vector machine technique［J］.Engineering Structures，2005，27（12）：1762－1773.

［21］Mo Y.Applications of SVR to the aveiro discretization method［EB／OL］.［2014－08－01］.http：∥link.springer.com／article／10.1007／s00500－014－1379－51fulltext.html.

Error correction method for support vector regression

CHEN Jun1，3，PENG Xiao-qi1，2，TANG Xiu-ming3，SONG Yan-po1，LIU Zheng1
（1.School of Information Science and Engineering，Central South University，Changsha 410083，China；2.Department of Information Science and Engineering，Hunan First Normal University，Changsha 410205，China；3.Institute of Information and Electrical Engineering，Hunan University of Science and Technology，Xiangtan 411201，China）

The influence of the local support vector on the prediction results is not fully considered in the traditionalε-insensitive support vector regression（ε-SVR），which is not conducive to improve the predictive accuracy of regression problems.An error correction method is proposed forε-SVR，in which the minimum sum of Euclidean distances between ideal values andε-SVR regression values and local support vectors are taken as the objective function，and the width ofε-insensitive loss tube（ε-tube）is taken as constraint to correct the error in terms of local support vector on and out of theε-tube boundary in high dimensional feature space.Simulation using artificial datasets with different distributed and UCI benchmark data sets shows that the proposed method has higher prediction and generalization performance.

support vector regression（SVR）；error correction；prediction accuracy；generalization

TP 181

10.3969／j.issn.1001-506X.2015.08.18

陈君（1977－），男，讲师，博士研究生，主要研究方向为智能决策、工业过程优化决策。

E-mail：97chenjun＠163.com

彭小奇（1962－），男，教授，博士，博士研究生导师，主要研究方向为系统建模、智能决策、工业过程优化决策。

E-mail：pengxq＠csu.edu.cn

唐秀明（1977－），女，讲师，博士研究生，主要研究方向为智能决策、电力系统负荷建模。

E-mail：tangxm2873＠sina.com

宋彦坡（1979－），男，副教授，博士，主要研究方向为智能决策、工业过程优化决策支持。

E-mail：songyanpo＠csu.edu.cn

刘征（1979－），女，博士研究生，主要研究方向为工业过程优化决策与控制。