多无人机集结问题分布式求解方法

2015-05-25符小卫崔洪杰高晓光

系统工程与电子技术 2015年8期

关键词：航迹控制算法一致性

符小卫，崔洪杰，高晓光

（西北工业大学电子信息学院，陕西西安710129）

多无人机集结问题分布式求解方法

符小卫，崔洪杰，高晓光

（西北工业大学电子信息学院，陕西西安710129）

针对多无人机协同对地打击的任务区集结问题，建立了基于一致性理论的分布式控制结构，设计了结合航迹规划与轨迹控制的策略以实现多无人机同时到达。以提高一致性算法收敛速度为目的，引入状态观测器，改进了含有虚拟Leader的一致性控制算法，并对新算法的收敛性和快速性进行了数学证明。仿真结果表明，本文的方法能够有效实现多无人机同时集结到目标位置，改进的算法具有更快的收敛速度。

多无人机；集结；一致性理论；分布式控制

0 引言

随着通信网络技术与计算机技术的发展，战场环境日趋复杂，单架无人机已无法满足作战需要，多架无人机协同执行任务将是未来信息化战场上无人机作战运用的主要形式［1］。为了提高攻击的有效性，最大化杀伤效果，通常要求多架无人机能够同时到达各自目标位置执行协同打击任务。此类同时到达问题也称为同时集结问题，主要包括航迹规划和轨迹控制两方面研究内容。针对此类集结问题，文献［2－3］研究了基于协调变量和协调函数的多无人机协同航迹规划方法，但是该方法本质上仍是集中式控制方法，存在信息交互量大、计算复杂且鲁棒性差的缺点。近年来，多智能体一致性理论的研究取得长足进展，已经成功应用到了信息融合［4－5］、编队控制［6］、任务分配［7］和编队集结［8－12］等领域。基于局部信息交换的一致性控制方法不依赖于中央控制单元，相对于集中式控制方法来说更加便于协调各无人机的行为，是未来信息化、网络化战场环境下实现多无人机任务协同和自组织作战的有效控制方法。文献［8］研究了有无通信噪声下多无人机同时到达的一致性控制算法；文献［9］建立了多导弹分布式协同制导的控制结构，提出了一种结合一致性协调算法和导引律的协同制导方法；文献［10］建立了基于移动自组网的多无人机网络化控制结构，给出了应用一致性理论解决集结问题和编队控制问题的简单例子；文献［11］针对复杂网络条件下多无人机系统任务区集结问题，提出了多机非合作求解方法，使多无人机系统具有较强的动态响应能力；文献［12］研究了基于一致性理论的分散化控制方法，设计了多种控制策略。但是，以上文献的研究都少有考虑一致性算法收敛速度的问题，而在信息化复杂战场环境下，战场态势瞬息万变，系统状态快速地实现一致能够提高多无人机协同控制与任务执行的效率，因此有必要对一致性算法的收敛速度展开研究。

本文针对多无人机协同对地打击的任务区集结问题，设计了结合航迹规划与轨迹控制的分布式求解方法，并以提高收敛速度为目的，改进了含有虚拟Leader的一致性算法，该算法既能灵活地控制无人机的运动，又能快速地实现无人机的任务协同，仿真验证了本文的方法能够有效实现多无人机同时集结到目标位置。

1 多无人机集结问题

1.1 问题描述

假定在某次任务中，由n架无人机组成的多机编队分别由不同的机场起飞，从不同方向集结到某一任务区域并执行协同对地打击任务。在整个任务执行过程中，需要综合考虑敌方探测雷达、防空导弹威胁、禁飞区及无人机平台性能等约束条件，实时动态地规划每架无人机的飞行航迹。为了达成打击行动的突然性，最大化协同打击的杀伤效果，要求所有无人机能够同时到达各自的目标位置。

图1是典型的多无人机集结任务想定示意图，其中3架无人机要同时集结到任务区域执行协同打击任务，图中虚线所示是预先规划好的航迹，在飞行过程中，UAV2发现突发威胁，需要进行航迹重规划，如图中实线所示，同时UAV2通过机间通信网络交换协调变量信息，即预计到达时间（estimated time of arrival，ETA），其他各架无人机也会根据接收到的信息和自身飞行状况来调整预先规划好的航迹和飞行速度，从而确保所有无人机能够同时集结到任务区域。

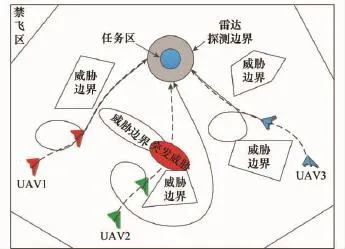
图1 典型多无人机集结任务想定

1.2 无人机运动模型

假设多无人机在相同二维平面，即无人机做定高飞行，则对于第i架无人机，其动态特性可采用如下运动学模型［11－12］描述：

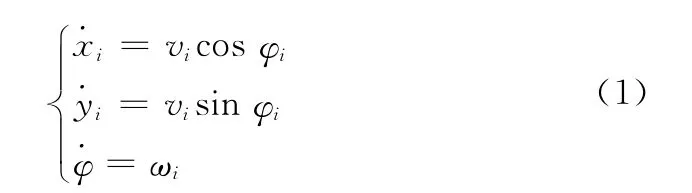
式中，（xi，yi）为第i架无人机的位置向量；vi、φi和ωi分别为飞行速度、航向角和航向角速度。航向角速度变化率ωi和飞行速度vi满足：

式中，ωhead、vmin、vmax为无人机的平台物理特性约束所决定。

假定每架无人机的自动驾驶仪具有航向保持和速度保持能力，其数学描述为

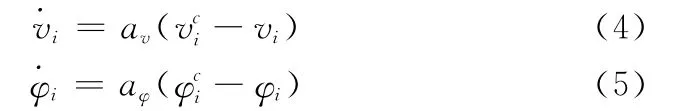
1.3 网络通信关系模型

对于一个分布式协同控制无人机系统，多无人机之间的网络通信关系可由一个加权的有向图G＝（V，E，A）来描述。V＝｛v1，v2，…，vn｝为图的节点集合，对应无人机平台；E⊆V×V为有向边集合，边（vi，vj）表示第j架无人机可以将信息发送给第i架无人机，由于G为有向图，故通常情况下（vi，vj）≠（vj，vi）；A＝［aij］为邻接矩阵，其非负元素aij的取值与图中的边相对应，它描述了多无人机通信连接关系，例如，（vi，vj）∈E⇔aij＞0。定义节点vi的相邻节点集合为Ni＝｛vj∈V∶（vi，vj）∈E｝。为研究方便，通常采用有向图对应的Laplacian矩阵L＝［lij］来描述网络拓扑结构，其中

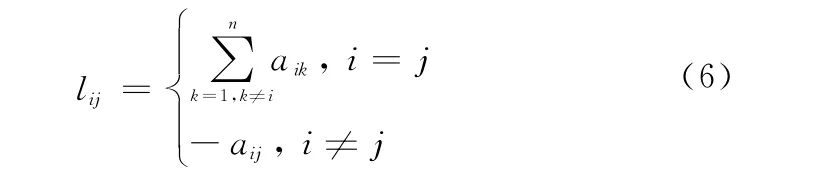
2 分布式控制结构

基于一致性理论的多无人机集结问题的分布式控制结构如图2所示，其中第i架无人机的预计到达时间为协调变量。航迹规划器（path plan，PP）根据无人机状态信息、禁飞区和威胁信息，规划航迹；航迹平滑器（path smooth，PS）接收航迹规划器输出的航路点序列，按照运动学模型和无人机平台性能约束平滑航迹，从而产生可飞航迹；分布式协调器（distributed coordinate，DC）通过分布式通信网络接收相邻无人机的ETA，应用一致性控制算法产生速度调节指令，通过调整自身飞行速度来协调ETA，再根据规划出的航迹以及运动学模型计算航向调节指令；自动驾驶仪（autopilot，AP）接收速度调节指令和航向调节指令，控制无人机平台运动。

显然，应用一致性算法产生速度和航向调节指令的DC模块是整个分布式控制结构的核心。设任务开始的时刻为时间轴的零点，即t＝0时刻，Li为第i架无人机在t时刻距离目标位置的剩余路径长度，vi为第i架无人机在t时刻的飞行速度，则

则每架无人机的预计到达时刻为

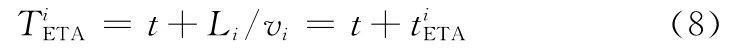
对式（8）作微分运算，有

进一步整理得到速度参考指令：

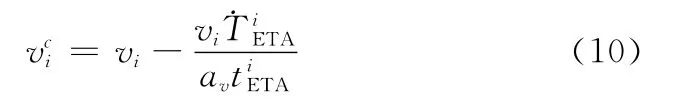
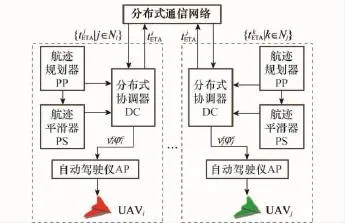
图2 分布式控制结构

3 分布式控制方法

3.1 基本一致性算法

采用一阶微分方程描述无人机的状态：

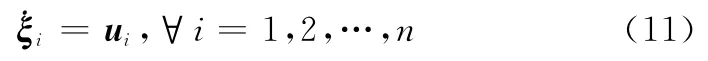
式中，ξi∈Rm和ui∈Rm分别为第i架无人机的信息状态和控制输入。如果对于任一初值ξi（0）和所有i，j＝1，2，…，n，当t→∞时，‖ξi－ξj‖→0，则称多无人机系统状态达到一致。采用如下基本一致性控制算法［13］：

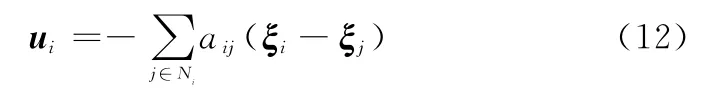
式中，aij为多无人机通信拓扑图邻接矩阵A中相应的元素。

由式（12）作为控制输入，多无人机系统的状态方程用矩阵表示为

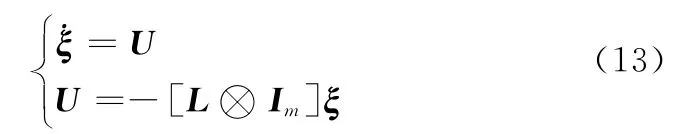
引理1［14－15］在时不变通信拓扑条件下，基于式（13）的多无人机系统状态实现一致的充要条件为有向通信拓扑图G含有一簇有向生成树，其代数判据为Re（λ2（L））＞0。

式中，ui为一致性算法计算得到的控制输入。因此，求解多无人机集结问题的关键就转化为设计有效的一致性算法。

3.2 改进的基于虚拟Leader的分布式控制方法

在多无人机协同控制中，群体Leader和虚拟Leader有着重要应用，基于此，文献［12］提出了一种含虚拟Leader的分布式控制算法：

式中，系数βi为第i架无人机与虚拟Leader通信链路的权值。

令L′为引入虚拟Leader之后的Laplacian矩阵，则多无人机系统的状态方程用矩阵表示为

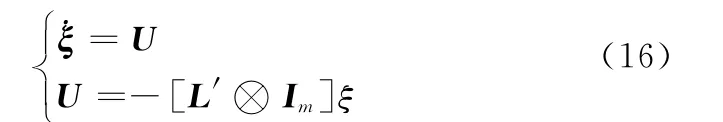
在引入含有虚拟Leader的一致性控制算法下，所有无人机的ETA将与虚拟Leader的ETA趋于相同。这种方法的优点是操作员可以通过修改速度调节指令vc0来灵活控制虚拟Leader运动，从而实现对整个无人机编队的控制。

但是，该方法并没有考虑一致性算法的收敛速度问题，为此，本文引入状态观测器［16］，基本思想是：每架无人机对自身的未来状态进行预测，通过局部信息交换将预测状态传递给相邻无人机，再利用预测状态构造控制算法，从而使多无人机系统状态更快地达到一致。

在一致性控制算法中引入状态预测器˙ξP＝－（L′⊗Im）ξ，有助于多无人机系统状态更快地演化到一致。则

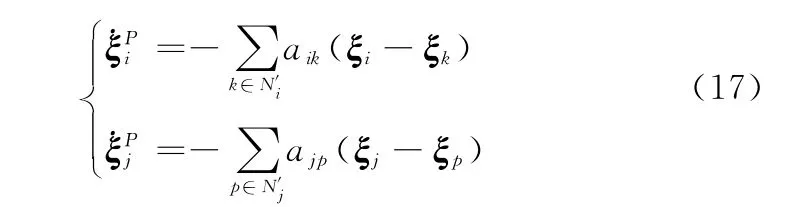
式中，N′i、N′j为加入虚拟Leader之后的邻居集合。

加入状态预测补偿之后，设计如下控制算法：

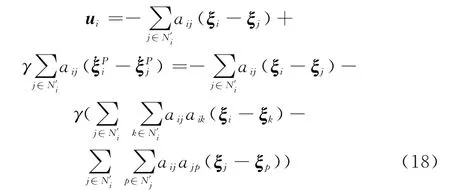
式中，γ为状态预测器的影响因子。

在一致性控制算法式（18）下，多无人机系统状态方程用矩阵表示为

3.3 新方法的收敛性和快速性证明

定理1 采用一致性控制算法式（18），若包含虚拟Leader的有向通信拓扑图G中含有一簇有向生成树，且G是对称的，则式（19）下的多无人机系统能够实现状态一致，且较无状态预测器的多无人机系统（16），能够更快地演化到一致。

证明设L′的特征根为λ1，λ2，…，λn，如果有向通信拓扑图G含有一簇有向生成树，则有λ1＝0，0＜Re（λ2）≤…≤Re（λn）。进一步，L′是对称矩阵，那么0＜λ2≤…≤λn。设L′＋γL′2的特征根为，则有

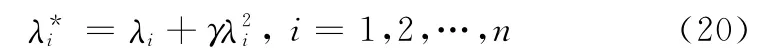
则对于∀γ＞0，有0＝λ＊1＜λ＊2≤…≤λ＊n，λ2＜λ＊2，根据定理1，在一致性控制算法式（18）下，多无人机系统状态能够实现一致。并且，加入状态预测器之后系统有更大的最小非零特征根，由文献［15］可知多无人机系统（19）具有更快的收敛速度。

证毕

4 集结问题分布式求解步骤

综上所述，多无人机集结问题的分布式求解步骤如下：

步骤1 根据敌方威胁、禁飞区以及平台性能等约束条件，计算每架无人机的飞行路径航路点序列：

Pathi＝｛starti，waypoint1i，…，endi｝，i＝1，2，…，n

步骤2 计算每架无人机的航迹长度Li，从而求得速度约束式（3）下ETA的范围。定义集合TiETA＝｛Li／vmax，Li／vmin｝。若

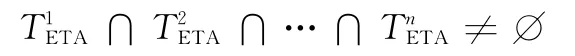
执行步骤3；否则，跳转至步骤1。

步骤3 每架无人机通过机间通信网络和邻居无人机交换TiETA。

步骤4 由式（14），根据一致性控制算法，计算速度调节指令vci。

步骤5 利用规划出的航迹信息和运动学模型，计算航向调节指令φci。

步骤6 将速度调节指令vci与航向调节指令φci发送给自动驾驶仪，实现对无人机平台的速度和航向控制。若各无人机同时到达目标点，则算法结束；若遇到突发威胁，则跳转至步骤1进行航迹重规划。

5 仿真结果与分析

为了验证本文方法的有效性，在VC＋＋6.0下建立多无人机集结问题仿真环境。设定任务区为50km×50km，分布着5个有着不同作用范围的已知威胁，即T1-T5，其中T5也为任务目标。3架无人机初始速度分别为200m／s、150m／s和180m／s，起始位置分别为（5km，10km）、（25km，11km）和（46km，12km），目标位置分别为（20km，40km）、（25km，35km）、（30km，40km）。假定无人机平台性能参数为Rmin＝300m，av＝0.2，aφ＝0.05，ωhead＝1.2rad／s，vmin＝120m／s以及vmax＝220m／s。无人机之间的通信拓扑图如图3所示。

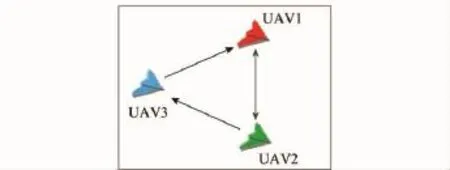
图3 多无人机通信拓扑

算例1 采用基本一致性算法式（12）实现多无人机同时到达。首先，本文采用改进稀疏A＊搜索算法作为航迹规划算法，并进行航迹平滑处理，为无人机规划出可飞航迹如图4所示。

计算得到3架无人机的初始可飞航迹长度分别为34.8km、24.3km、32.6km。在基本一致性控制算法下，得到的仿真结果如图5所示。

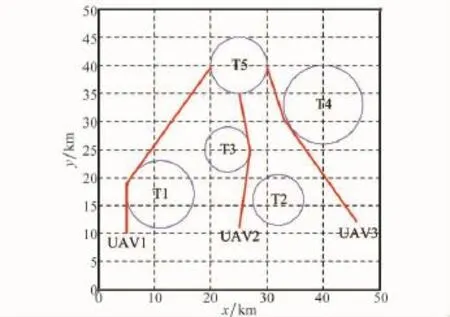
图4 多无人机初始可飞航迹

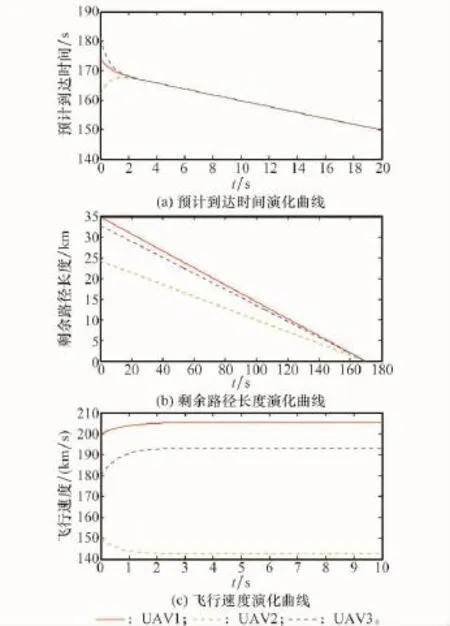
图5 算例1仿真结果

从仿真结果可以看出，经过大约2.5s的动态调整飞行速度的时间，3架无人机的ETA趋于一致，此后无人机的飞行速度保持恒定，并且无人机还有一定的速度调整裕量以应对突发威胁，整个集结任务耗时约170s。由此可见，采用本文的方法可以实现多无人机同时集结到指定目标位置。

算例2 如图6所示，引入一架虚拟的无人机，记为UAV0，其初始可飞航迹长度设为30km，速度协调指令设为180m／s。假定UAV2在飞行过程中遭遇突发威胁而进行航迹重规划，如图7所示，重规划后路径长度增加4.8km。采用一致性控制算法式（15），得到的仿真结果如图8所示。

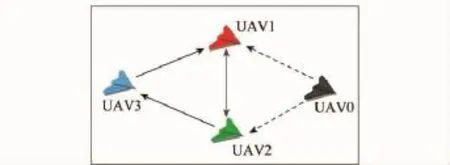
图6 引入虚拟Leader的通信拓扑

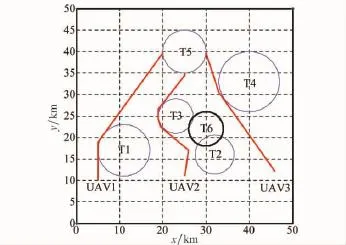
图7 重规划后的航迹

图8 算例2仿真结果

由图8可以看出，引入了虚拟Leader之后，各无人机都与虚拟Leader的ETA趋于一致。在任务开始30s后，UAV2发现突发威胁而进行航迹重规划，导致预计到达时间与剩余路径增大，各无人机再次通过动态调整飞行速度，最终同时到达目标位置，ETA仍与虚拟Leader保持一致。由此可见，在引入了虚拟Leader的一致性控制算法下，各无人机可以按照预先指定的时间同时集结到目标位置，操作人员可以通过设定速度协调指令控制虚拟Leader的运动，从而灵活控制各无人机的运动。

算例3 在算例2的基础上，改用本文提出的一致性控制算法式（18），取状态预测器的影响因子γ＝1，得到的仿真结果如图9所示。

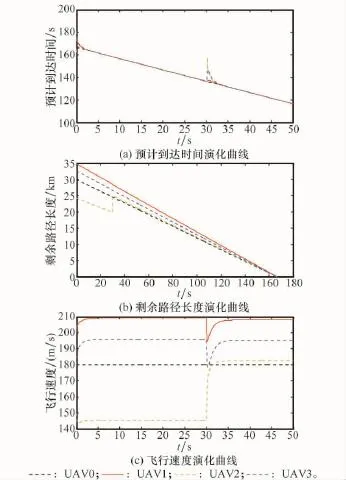
图9 算例3仿真结果

对比图8与图9，可以看出，加入状态预测器之后多无人机系统的ETA演化到一致的时间明显减少，算例2中两次动态调整时间分别为7.6s、9.1s，算例3中两次动态调整时间分别为4.1s、5.0s，一致性算法收敛速度分别提高46.1%、45.1%。因此，本文提出的改进一致性算法是合理并有效的，更加适用于动态变化的战场环境，使各无人机的ETA快速地实现一致。改变状态预测器的影响因子γ的值，一致性算法的收敛速度也会随之变化，但同时也对无人机飞行速度的调整提出了更高的要求，在实际应用中，需要考虑无人机的物理限制来合理化γ的取值。另外，也可以通过修改虚拟Leader的速度指令和盘旋飞行来协调各无人机的飞行速度。

6 结论

（1）本文提出了基于一致性理论的多无人机集结问题分布式求解方法，设计了结合航迹规划与轨迹控制的策略来实现多无人机同时到达。

（2）以提高一致性算法收敛速度为目的，在文献［12］控制算法的基础上，引入状态观测器对算法进行改进，使得多无人机系统状态更快地实现一致，从数学证明和仿真实验两方面验证了本文新算法的快速性和收敛性，能够快速有效实现多无人机的任务协同。

（3）仿真验证了本文的方法可以有效实现多无人机同时集结到任务区域。在面对突发威胁时，将航迹重规划与速度调整相结合，仍然能够确保多无人机同时到达。

［1］Office of the Secretary of Defense.Unmanned Systems Roadmap2007－2032［R］.Washington DC：DoD，2007.

［2］Nelson D R，McLain T W，Beard R W.Experiments in cooperative timing for miniature air vehicles［J］.Journal of Aerospace Computing，Information，and Communication，2007，4（8）：956－967.

［3］McLain T W，Beard R W.Coordination variables，coordination functions，and cooperative-timing missions［J］.Journal of Guidance，Control，and Dynamics，2005，8（1）：150－161.

［4］Morbidi F，Freeman R A，Lynch K M.Estimation and control of UAV swarms for distributed monitoring tasks［C］∥Proc.of the American Control Conference，2011：1069－1075.

［5］Casbeer D W，Beard R W.Distributed information filtering using consensus filters［C］∥Proc.of the American Control Conference，2009：1882－1887.

［6］Lin Z Y，Francis B，Maggiore M.Necessary and sufficient graphical conditions for formation control of unicycles［J］.IEEE Trans.on Automatic Control，2005，50（1）：121－127.

［7］Moore K，Lucarelli D.Decentralized adaptive scheduling using censensus variables［J］.International Journal of Rubust and Nonlinear Control，2007，17（10／11）：921－940.

［8］Kingston D B，Ren W，Beard R W.Consensus algorithms are input-to-stable［C］∥Proc.of the American Control Conference，2005：1686－1690.

［9］Zhao S Y，Zhou R.Cooperative guidance for multimissile salvo attack［J］.Chinese Journal of Aeronautics，2008，21（6）：533－539.

［10］Jaimes B，Jamshidi M.Consensus-based and network control of UAVs［C］∥Proc.of the International Conference on System of Systems Engineering，2010：1－6.

［11］Zhang Q J，Wang J S，Jin Z Q，et al.Non-cooperative solving method of multi-UAV rendezvous problem in complex network［J］.Journal of Southeast University（Natural Science Edition），2013，43（S1）：32－37.（张庆杰，王俊生，金忠庆，等.复杂网络条件下多UAV集结问题非合作求解方法［J］.东南大学学报（自然科学版），2013，43（S1）：32－37.）

［12］Yuan L P，Chen Z J，Zhou R，et al.Decentralized control for simultaneous arrival of multiple UAVs［J］.Acta Aeronautica et Astronautica Sinica，2010，31（4）：797－805.（袁利平，陈宗基，周锐，等.多无人机同时到达的分散化控制方法［J］.航空学报，2010，31（4）：797－805.）

［13］Ren W，Beard R W.Distributed consensus in multi-vehicle cooperitave control：theory and applications［M］.Beijing：Publishing House of Electronics Industry，2014：24－37.（任伟，比尔德·兰德尔·W.多航行体协同控制中的分布式一致性：理论与应用［M］.北京：电子工业出版社，2014：24－37.）

［14］Ren W，Beard R W.Consensus seeking in multiagent systems under dynamically changing interaction topologies［J］.IEEE Trans.on Automatic Control，2005，50（5）：655－661.

［15］Olfati-Saber R，Murray R M.Consensus problems in networks of agents with switching topology and time-delays［J］.IEEE Trans.on Automatic Control，2004，49（9）：1520－1533.

［16］Xi Y G，Huang W，Li X L.Consensus of multi-agent system with state predictor［J］.Control and Decision，2010，25（5）：769－772.（席裕庚，黄维，李晓丽.具有状态观测器的多智能体系统一致性研究［J］.控制与决策，2010，25（5）：769－772.）

Distributed solving method of multi-UAV rendezvous problem

FU Xiao-wei，CUI Hong－jie，GAO Xiao-guang
（School of Electronics and Information，Northwestern Polytechnical University，Xi’an 710129，China）

To solve the rendezvous problem in the mission area of cooperative attack for multiple unmanned aerial vehicles（UAVs），a distributed control architecture based on the consensus theory is built and a strategy which combines path plan and trajectory control is designed to realize the simultaneous arrival of the multiple UAVs.To increase the convergence speed of the consensus algorithm，a state predictor is introduced to improve the performance of the consensus control algorithm which contains the virtual leader.Theorem about convergence and efficiency of the new algorithm is introduced with the mathematical proof.Simulation results show that the simultaneous arrival of the multiple UAVs can be realized by the proposed distributed solving method and the improved algorithm has faster convergence speed.

multiple unmanned aerial vehicles（UAVs）；rendezvous；consensus theory；distributed control

V 279，TP 273

10.3969／j.issn.1001-506X.2015.08.13

符小卫（1976－），男，副教授，博士后，主要研究方向为无人机任务规划与指挥控制。

E-mail：fxw＠nwpu.edu.cn

崔洪杰（1991－），男，硕士研究生，主要研究方向为多无人机协同控制与任务规划。

E-mail：chj819356695＠163.com

高晓光（1957－），女，教授，博士，主要研究方向为航空火力控制与作战效能分析。

E-mail：cxg2012＠nwpu.edu.cn

1001－506X201508－1797－06

网址：www.sys－ele.com

2014－09－05；