基于主动轮廓模型的SAR图像分割方法综述

2015-05-25涂松，李禹，粟毅

系统工程与电子技术 2015年8期

关键词：轮廓形状像素

涂松，李禹，粟毅

（国防科学技术大学电子科学与工程学院，湖南长沙410073）

基于主动轮廓模型的SAR图像分割方法综述

涂松，李禹，粟毅

（国防科学技术大学电子科学与工程学院，湖南长沙410073）

针对合成孔径雷达（synthetic aperture radar，SAR）图像分割这一研究热点，综合论述了基于主动轮廓模型（active contour model，ACM）的SAR图像分割方法。首先，介绍了经典的ACM及其数学原理，并通过理论和实验分析了这些模型应用于SAR图像分割时存在的问题；然后，对目前基于ACM的SAR图像分割方法进行了系统的梳理和分类讨论；最后，对基于ACM的SAR图像分割方法作了总结，并对将来的研究方向进行了展望。

合成孔径雷达图像分割；主动轮廓模型；统计建模；凸优化；相似性度量

0 引言

合成孔径雷达（synthetic aperture radar，SAR）以其全天时、全天候、大尺度、远距离和一定穿透性的优点，弥补了光学成像的不足，然而SAR图像中的相干斑噪声使目标与背景之间的边界变得十分模糊，如何搜索目标的最优边界以获取准确的目标轮廓和结构是SAR图像分割领域的研究难点。

传统的图像分割方法对于边缘和线的检测，被广泛地认为是自主的自底向上的过程［1］，即：只能依赖于图像本身获得的低层信息，不可利用高层理解信息，低层的计算误差传播到高层后，没有修正机会，所以容易受图像的噪声等复杂因素的影响。主动轮廓模型由于加入了高层理解机制，即：由外部约束力和图像力共同作用的能量泛函最小化来引导初始轮廓不断地向目标边界移动。比传统的图像分割方法更加符合图像分割的定义，提高了目标提取的准确性［2］，为解决SAR图像分割的研究难点提供了一种新的途径。

自snake模型［3］提出以来，陆续出现了测地线主动轮廓（geodesic active contour，GAC）模型［2，4］、CV（Chan and Vese）［5－6］、区域拟合（region-scalable fitting，RSF）模型［7－8］、局部高斯分布拟合（local Gaussian distribution fitting，LGDF）模型［9］和局部与全局强度拟合（local and global intensity fitting，LGIF）模型［10］等经典的主动轮廓模型，以及其他根据具体应用背景提出的一些改进模型［10－13］。按照能量泛函的定义，这些主动轮廓模型大体可以分为3类：基于边缘的模型、基于区域的模型以及两者的混合模型。这些方法易于加入图像特征，对噪声更鲁棒，得到的结果无需进行诸如边界连接、区域合并等后处理，能够更直接自然地表示边界和区域［14］，具有重要的理论和应用价值。近几年，有些学者成功地将主动轮廓模型应用于SAR图像分割，然而目前关于主动轮廓模型的综述大多是针对2008年以前的部分主动轮廓模型［1，15－18］，并且主要侧重于某一类模型或者是用于医学和光学图像分割的模型，对用于SAR图像分割的主动轮廓模型的综述较少。

本文对经典的主动轮廓模型（active contour model，ACM）进行了梳理，并分析了将其直接应用于SAR图像分割时存在的问题。然后，根据可利用的图像特征，结合最新的数学方法，对基于主动轮廓模型的SAR图像分割方法进行了分类讨论和研究，主要包括：基于能量泛函凸优化的ACM、基于区域统计信息的ACM、基于目标形状先验知识的ACM以及基于像素相似性度量的ACM，阐述了这些方法所建立的基础模型和原理。最后展望了基于主动轮廓模型的SAR图像分割方法的发展方向。

1 经典ACM及其用于SAR图像分割的问题分析

1.1 经典ACM

主动轮廓模型的基本思想是将分割目标的轮廓看作一条可变形的曲线，在基于变分法和偏微分方程求解能量泛函最小化的引导下，轮廓线从初始位置不断地向目标边界演化。根据能量泛函的定义，经典的主动轮廓模型可以分为三类：基于边缘的模型［2－4］、基于区域的模型［5－11］以及两者的混合模型［12－14，19－24］。

1.1.1 基于边缘的ACM

（1）参数化ACM

参数化主动轮廓模型［3，25－27］是采用显式方法描述轮廓的模型，即：这类模型将轮廓描述为一条带参变量的曲线，其中最具代表的是开创了主动轮廓模型用于目标边界检测时代的经典snake模型：

式中，α，β，λ＞0；一阶微分｜C′（s）｜表示由轮廓C（s）伸缩产生的弹性能量；二阶微分｜C″（s）｜表示因轮廓C（s）弯曲产生的曲率能量，两者的加权之和组成了给定图像u0的内部能量；弹性系数α和强度系数β分别控制轮廓沿法线方向朝目标演化的速度和曲线的光滑程度。

由式（1）可知，snake模型集成了控制轮廓伸缩和弯曲方式的内部能量以及表示图像边缘强度的外部能量。相比传统的图像分割方法，这类模型是一种全新的采用自上而下机制的图像目标提取方法，有效地利用了高层信息［1］。然而，参数化主动轮廓模型对曲线的显式表达，使轮廓的求解比较复杂且不利于描述轮廓的拓扑变化（如：轮廓的分裂、合并等）；其次，snake模型还对轮廓初始位置敏感和对凹域的收敛性不佳［28］。

（2）基于水平集函数的ACM

文献［29］提出的水平集方法解决了曲线参数化求解的繁琐问题。受水平集思想的启发，文献［4］将基于能量泛函最小化的经典snake模型和基于曲线演化理论的几何主动轮廓模型［2］联系了起来，提出了在黎曼空间中进行最小距离度量的GAC模型，其水平集演化方程为

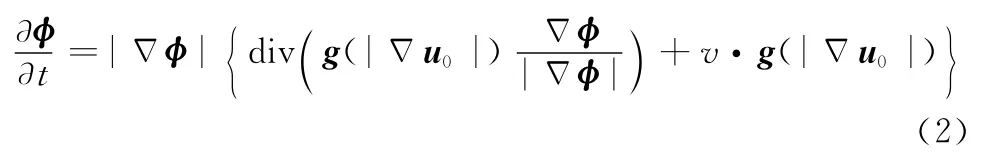
测地线主动轮廓模型利用水平集函数φ来隐式地表示曲线（即：只找出形状，但不对其进行参数化），能更好地描述曲线的拓扑结构变化，在迭代中轮廓自然地分裂和合并，克服了参数化主动轮廓模型对轮廓凹面、尖锐角点等难以处理的弊端［4，28］。

综上，基于边缘的主动轮廓模型比传统的基于边缘检测的分割方法有了进步［1，2，4－5，28］，但由于这类模型仍然建立在图像边缘检测的基础上，所以与传统图像分割方法具有相同的局限性，如边界漏损、对噪声敏感等问题［28］。其次，由于现有的基于水平集的SAR图像分割方法一般利用符号距离函数表示水平集函数，往往需要在曲线演化过程中进行耗时的重新初始化步骤，所以模型的计算效率低［30］且很难实现精确求解［28］。另外，由于这些模型的能量泛函仍然是非凸的［31］，所以模型最终的分割结果仍与初始轮廓的位置有关。

1.1.2 基于区域的ACM

基于区域的主动轮廓模型直接使用轮廓内部和外部区域的像素强度信息，不再使用梯度信息，所以具有一定的抗噪性。按照能量泛函中区域能量项的定义，可以分为以下3种类型：

（1）基于分片光滑函数拟合的ACM及其简化

文献［32］通过分片光滑函数的最佳逼近（即著名的Mumford-Shah泛函）来解决目标边界检测问题，文献［5］给出了用于图像分割的Mumford-Shah泛函的简洁形式：

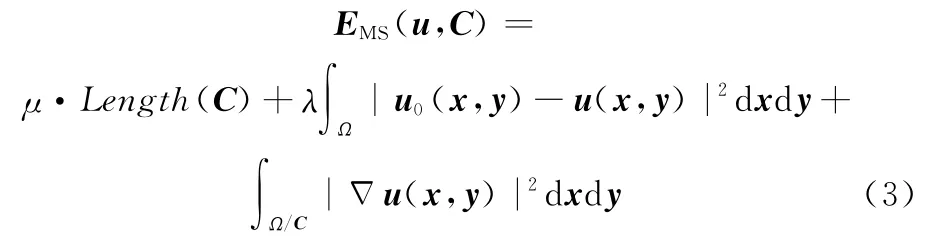
式中，变量函数u（x，y）为定义于Ω／C上的图像。Mumford-Shah模型通过最小化能量泛函（3）来求解图像u0的最佳逼近函数u，该最优解u由若干平滑区域及其边界构成。Mumford-Shah模型比snake模型的优势在于其能量泛函后两项的叠加提供了总体变差最小的机制，而长度项控制了曲线的光滑程度，所以该模型将图像的去噪和真实边缘的恢复统一在一个模型中，控制了低层的误差扩散，而snake模型对噪声敏感。然而Mumford-Shah模型用数值逼近方法实现时很困难，这成为该模型应用的主要障碍。为此，出现了很多Mumford-Shah模型的简化和近似实现方法，如：文献［33］提出的椭圆形变分模型，文献［34］提出的有限差分模型等。

（2）基于分片常数拟合的ACM及其改进

文献［5］提出了对Mumford-Shah模型更加简化的实现方法－分片常数拟合的Mumford-Shah模型（又称CV模型）：

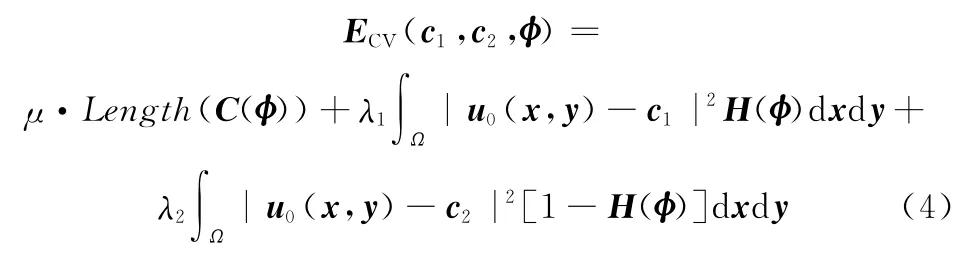
式中，μ≥0，v≥0，λ1，λ2＞0；H（φ）为Heaviside函数。

由式（4）可知，CV模型不含图像的梯度项，所以也被称为无边缘（或无梯度）的主动轮廓模型，它克服了传统的基于梯度信息分割方法的困扰。然而正如式（4）所示，CV模型的分割原理在本质上是利用分段常量ci来表示分片光滑区域的均值，再利用能量泛函最小化方法来最优逼近均值相似的区域，所以只对均匀图像分割较好。

为了对不均匀的图像进行分割，尺度可调的RSF模型［7－8］将CV模型的全局强度拟合函数（如式（4）中的｜u0（x，y）－ci｜2）改造为局部强度拟合函数｜u0（x，y）－fi｜2，其中fi（x）称为局部强度拟合函数，主要作用是拟合像素点x局部邻域的强度均值，这一局部特性对不均匀图像分割起到关键作用，却使RSF模型的能量泛函在轮廓演化过程中容易陷入局部极小值（如文献［10］中图2所示）。也有学者提出用基于局部区域统计建模的主动轮廓模型来处理不均匀图像的分割问题，如LGDF模型［9］用高斯分布描述不均匀图像的局部区域，并替换RSF模型中的局部强度拟合函数。LGDF模型采用高斯分布代替RSF模型局部强度拟合函数的意义在于它将区域统计建模的思想引入到了ACM模型中，然而SAR图像的统计分布多呈现非高斯重拖尾的统计特性，所以直接将基于高斯分布来进行不均匀区域拟合的LGDF模型用于SAR图像分割，在理论上，我们可以推测LGDF模型无法准确地拟合SAR图像同质区域（实际上通过图1的实验观察，也可以得出这个结论）。

统计模型对局部区域统计特性拟合的精确度对SAR图像分割效果起决定作用，那么统计模型的选取值得研究。如何将更合适的分布模型引入到主动轮廓模型，已经成为一个研究热点［11－12，35］。

（3）基于区域的组合ACM

近几年，有学者提出了将全局区域拟合能量与局部区域拟合能量相结合的组合模型，克服了单一模型在不均匀图像分割中易陷入局部极小值的缺陷。比如：LGIF主动轮廓模型［10］将RSF模型的局部信息和CV模型的全局信息综合考虑，使曲线在演化中局部强度拟合力和全局强度拟合力可以互补：

式中，0≤ω≤1为模型的权值。

类似于LGIF模型，还存在其他的组合模型，但都是对经典的CV、RSF和LGDF等模型的组合及其改进［19，31，36－38］。这些模型在不均匀的光学和医学图像分割中取得了显著的效果，但在SAR图像分割中的应用还很少。

1.1.3 基于边缘和区域的混合ACM

为了使主动轮廓模型既具有较好的边缘定位能力，又具有一定的抗噪性能，近几年出现了将基于边缘和基于区域的模型进行组合的主动轮廓模型。这类方法大多数是对第1.1.1节和第1.1.2节中模型的简单线性组合［19－21］，或者对模型的组合权值的研究［22－24］。

文献［39］提出的SBGFRLS模型组合了测地线模型和CV模型的优点，拥有局部和全局性质，对噪声更鲁棒。文献［19－20］将测地线模型提供的边缘信息、SBGFRLS模型与RSF模型提供的全局和局部区域统计信息通过线性加权的方式组合起来，设计了新的能量泛函。文献［21］将图像目标区域的二重积分通过Green公式转化为该区域边界上的曲线积分，并将其作为新的能量项直接引入到snake模型中，区域力的引入使轮廓曲线的演化对噪声更鲁棒。文献［22］采用全局最小路径的主动测地线约束基于区域的主动轮廓模型，克服了其容易陷入局部极小值的缺陷。文献［23］尝试用博弈论来实现基于边缘和基于区域主动轮廓模型的最优线性组合。

然而，这些混合主动轮廓模型中的权重都为固定的，对初始轮廓依赖度高或对不同图像适应性差。文献［24］采用可变权重设计了接力型组合模型（RACM），通过相邻两次迭代的轮廓长度改变量来控制CV模型和RSF模型依次进行工作，RACM模型对初始轮廓位置、大小和形状不太敏感，具有一定的抗噪性能。

1.2 经典ACM在SAR图像分割中的性能分析

上述的经典主动轮廓模型都是基于非相干的光学和医学图像得到的最优化模型。光学图像和医学图像中的噪声主要成因为成像系统的非线性，一般可以用高斯分布来描述［40］。而SAR图像中的斑点噪声是由于SAR系统的相干成像原理造成的，SAR系统接收到的总回波不完全由目标的散射决定，而是围绕这些散射系数值有一定的随机起伏，这种起伏在SAR图像上就表现为相干斑噪声。对相干斑噪声的描述，需要采用更加复杂的统计模型。这两类图像噪声之间的本质差异，导致经典主动轮廓模型无法对SAR图像取得较好的分割效果［40］。下面对其作进一步分析：

（1）基于边缘的ACM在SAR图像分割中的性能分析

由第1.1.1节对基于边缘的主动轮廓模型的综述可知这类模型的基本思想是：在特定能量泛函最小化的引导下，轮廓沿着法线方向运动，当处于目标边界时，轮廓停止演化。虽然水平集函数的引入使snake模型的参数化求解得到简化（如测地线模型［4］），且有利于描述轮廓的拓扑变化，具备了分割多目标的能力，但这类模型对目标边界的判断仍是基于图像的梯度Δu0，所以对噪声敏感是其必然缺陷。尤其在SAR图像中，由于相干斑噪声使SAR图像的目标边缘比较模糊，即使同质区域中也存在一定的灰度起伏和斑点噪声，造成目标边缘处梯度并非最大，模型的能量泛函在边缘也不一定到达最小值，所以演化的曲线会穿越边界，产生边界漏损，引起分割的不准确。通过能量泛函式（1）和式（2）很容易理解这一点，在此不作赘述。

（2）基于区域的ACM在SAR图像分割中的性能分析

第1.1.2节介绍的基于区域的模型及其组合模型，都是基于经典的CV、RSF和LGDF模型的改进或者这几种模型之间的两两组合。然而，我们发现这些模型能量泛函中的区域拟合函数都是基于形如L2范数｜u0（x，y）－fi｜2计算的，其本质上属于欧式距离的范畴，该距离越小表明像素点与该区域拟合函数值越相似，文献［35］通过理论推导给出了如下结论：

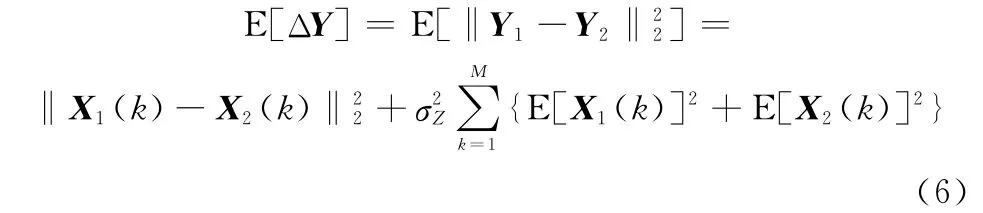
式中，X是真实的信号；Z是均值为1的乘性白噪声；Y为观测信号。Y1和Y2分别表示SAR图像中任意两块具有相同形状大小的局部区域观测值（式（4）的距离函数中的u0（x）可以看作局域Y1的特例，即仅含一个像素点的局域），M表示局部区域Y1和Y2中像素的数目。

如果在理想SAR图像的同质区域中，真实信号X可看作常量，则X的方差为0，所以式（6）的第二项为0，则E［ΔY］＝‖X1（k）－X2（k）‖22，此时观测信号变化的期望反映了真实信号的变化，因此这种情况下欧式距离能够度量像素的相似性。

然而，在SAR图像的目标边缘和纹理区域，不同局部区域真实信号X是变化的，所以式（6）的第二项也是变化的，则E［ΔY］≠‖X1（k）－X2（k）‖22，此时观测信号变化的期望不能反映真实信号的变化，且两者不一定呈线性关系，因此这种情况下欧式距离对SAR图像像素的相似度度量不再有效。

综上，在第1.1.2节提到的基于区域的模型中，由欧几里德距离定义的区域能量项将无法准确地反映区域能量变化，相应的能量泛函最小化也无法正确地引导轮廓的演化。另外，由文献［31］可知，上述基于区域的能量泛函均为非凸函数，所以轮廓在演化中还容易产生局部极小值，从而无法收敛到目标边界。

同理，基于边缘和区域的混合主动轮廓模型在SAR图像分割中的性能分析，可以参考本节的（1）和（2）中对各类模型的分析，本文对此不作进一步阐述。

图1（b）的实验结果表明经典snake模型在MSTAR数据库的T72图像分割中几乎无法向目标边界演化。这主要是由于snake模型的能量泛函（即式（1））是用可搜索到的图像特征的局部最小集合设计的，snake模型通过最小化该能量泛函来实现曲线的不断变形并向期望的轮廓靠近，直到曲线搜索到最大的｜Δu0（C（s））｜，这种方法本质上仍然是一种规范化的边缘检测问题，从而在斑点噪声的SAR图像分割中出现如本节（1）中所分析的病态问题［2］。

图1（c）～图1（f）中MSTAR数据库的T72图像分割实验表明这些经典的基于区域的主动轮廓模型在SAR图像分割中存在问题：CV模型完全检测不到目标边界；虽然RSF、LGDF和LGIF模型可以检测到目标边界，但在背景区域中都不同程度地存在一些无法继续演化的轮廓。主要原因在于CV、RSF和LGDF等模型的区域能量项都是基于欧式距离，而在本节（2）已经分析了在乘性噪声模型下，欧几里德距离不适用于度量SAR图像像素的相似度，以致在能量最小化过程中易陷入局部极小值。虽然LGIF模型将RSF模型和CV模型进行线性组合，在一定程度上对一些不均匀图像（如文献［10］的医学图像）的分割有着一定的鲁棒性，然而其本质上没有改变区域拟合能量项的构造方式，实验也证明了该模型在SAR图像分割中仍不可避免的会出现陷入局部极小值的轮廓。

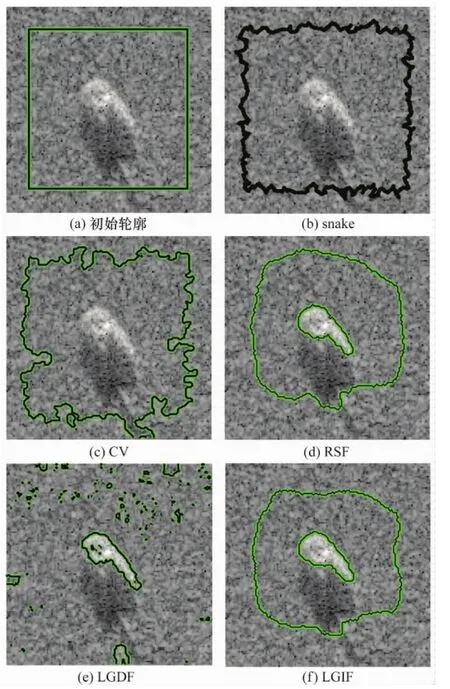
图1 经典ACM经过400次迭代后对T72图像的分割

2 基于ACM的SAR图像分割方法

为了克服经典主动轮廓模型在SAR图像分割中易陷入局部极小值的问题，根据可利用的图像特征，很多学者结合最新的数学方法，从不同的角度提出了改进方法，如：采用凸函数框架将非凸的能量泛函进行凸优化、引入更合适的区域统计信息或先验知识，以及具有学习能力的非线性映射模型等方法，这些方法与主动轮廓模型的成功结合，为主动轮廓模型实现SAR图像分割提供了新的途径。

2.1 基于能量泛函凸优化的ACM

由第1.2节对CV模型和RSF模型的分析可知，CV模型用分段常量对图像建模，不适合非均匀图像的分割；而RSF模型只用局部拟合均值对不均匀的图像进行建模是不准确的，尤其当不同局部区域的强度均值很相似的时候［41－42］；另外，RSF模型的能量泛函是非凸函数，所以其分割结果对水平集函数的初始化很敏感［41］。

文献［31］说明了图像处理和计算机视觉中的某些非凸问题可以用凸最小化方法来重新描述，从而可以通过标准的凸函数最小化框架找到非凸能量泛函的全局最小值，克服了局部极小值的缺陷，将文献［31］提出的全局最小化算法称为GMAC模型。

GMAC模型的提出为很多具有非凸能量泛函的主动轮廓模型实现全局最小值提供了理论依据。文献［43］将snake模型［3］、Rudin-Osher-Fatemi去噪模型［44］和Mumford-Shah分割模型［32］统一起来加入到GMAC框架中定义了新的凸能量泛函，并且在理论上证明了该主动轮廓模型全局极小值的存在。

关于主动轮廓模型能量泛函全局最小值的实现，大多数方法都是基于文献［31］的GMAC方法的凸优化。如文献［45］将RSF能量项引入到GMAC框架定义了凸的RSF模型，该模型克服了局部极小值的缺陷，对SAR图像的噪声更鲁棒。文献［41］用不同均值和方差的高斯分布来拟合不均匀图像的局部区域，并将该局部区域信息加入到GMAC框架定义了新的凸能量泛函，该模型应用于SAR图像分割效果优于RSF模型和文献［45］的凸RSF模型。

近些年也出现了其他的数学方法来实现主动轮廓模型能量泛函全局最小值的求解，如：文献［46］对传统的梯度下降算法进行了改进，提出了隧道梯度下降算法来克服局部极小值。也有学者从水平集函数在演化过程中如何保持平稳性的角度提出了相应的全局稳态主动轮廓模型［30，47－48］，如文献［47］发现基于区域的主动轮廓模型，只有当水平集函数φ的符号改变才能导致能量泛函发生变化，所以很多主动轮廓模型为了防止轮廓陷入局部极小值以获得稳定的演化，需要定期地将φ重新初始化为符号距离函数［2－3］，但这样做的计算复杂度很高，且何时重新初始化、如何初始化都没有一个简单易行的通用办法［46］。为此出现了一些水平集函数的改进方法［48］，例如文献［48］设计了一个水平集函数的惩罚项，使水平集函数在演化过程中始终为一个近似的符号距离函数，避免了水平集函数的重新初始化步骤。然而这种强制限定水平集函数近似为符号距离函数的方法不能保证得到的解仍然是稳态的，所以该方法可能仍然对轮廓的初始位置敏感［45］。文献［45］采用两个shifted Heaviside函数设计了新的能量泛函，并且从数学上证明了该模型具有全局稳态最小值。文献［30］用G0分布对SAR图像的区域建模，并将该分布函数加入到文献［47］的全局稳态最小值模型，实现了对高分辨率SAR图像的全局稳态最小值分割。

随着水平集方法的发展，将来还会有更多的主动轮廓模型通过上述全局最小值模型得到扩展，使模型对SAR图像分割更加鲁棒和稳定。

2.2 基于区域统计信息的ACM

由第1节分析可知，基于边缘的主动轮廓模型主要依据图像的梯度进行边界检测，虽然水平集方法的引入使基于snake模型的参数化轮廓的数值计算问题得到解决，但是轮廓的演化仍然很容易受到噪声的干扰，产生大量的局部最小代价函数。为此，很多学者将区域统计信息引入到主动轮廓模型，提高了模型的抗噪性和分割目标的准确性。

早在1996年，文献［42］就研究了用于图像分割的Mumford-Shah泛函和贝叶斯最大后验概率估计之间的联系：文献［42］中将图像I的一个最优分割P（Ω）通过最大后验概率p（P（Ω）｜I）来计算，然后借助贝叶斯准则p（P（Ω）｜I）∝p（I｜P（Ω））p（P（Ω）），用容易求得的条件概率p（I｜P（Ω））来定义基于区域统计信息的能量项。例如：如果我们假设图像域Ω可以被分割为若干子区域Ωi，并且这些子区域服从高斯分布，则基于区域统计信息的能量泛函可以构建为

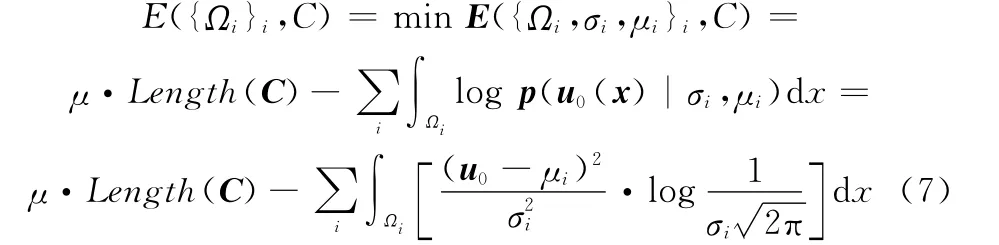
由式（7）可知，当子区域Ωi的方差σ2i为常数时，能量泛函式（7）为Mumford-Shah泛函（即式（3））的特例。

此后，贝叶斯框架已成为计算机视觉中处理很多病态问题的越来越流行的方法。然而，无论由贝叶斯理论构建的主动轮廓模型如何变化，其方法本质上都是将不同的低层信息（比如图像的强度、颜色、纹理等）整合到一个能量泛函中，构造出基于区域统计信息的主动轮廓模型。如文献［16］阐述了基于区域信息的分割方法能够采用一个通用的能量泛函框架：

式（8）的通用分割框架正是基于文献［42］中提到的贝叶斯框架构建的，其中f（x）为区域Ωi中不同位置对应的特征值，可以用独立同分布的随机过程来建模）是在参数成立的前提下，Ωi中随机过程的条件概率密度函数。

如果将水平集方法加入式（8）的分割框架，可以实现对很多经典的基于区域的主动轮廓模型的扩展。比如对CV模型的扩展可表示为

很多学者都是基于该框架将一些更复杂的区域统计信息纳入其中，提出了对含噪的医学图像或SAR图像很鲁棒的分割模型。如文献［12］采用对不均匀SAR图像的区域拟合能力更好的G0分布来计算区域能量泛函，其构建的主动轮廓模型能够适用于不同类型的SAR图像分割。文献［49］提出用灰度共生矩阵提取SAR图像目标区域的纹理特征，然后用主成分分析方法对特征进行优化，并将此纹理描述引入GMAC框架，定义了新的基于纹理描述的主动轮廓模型。文献［50］基于图像小波变换后的区域像素强度概率密度函数定义了相应的区域能量项。最近，也有学者将模糊函数引入基于区域统计信息的主动轮廓模型［51］，建立了模糊区域拟合的能量泛函，该能量泛函的模糊处理方法对光滑的目标边界定位起到较好的效果。

近几年，也有一些学者提出了将区域统计信息之间的距离度量引入主动轮廓模型的方法，增强了主动轮廓模型对SAR图像分割的鲁棒性，取得了较好的效果。如文献［52］将区域的实际概率密度函数与shifted－Rayleigh分布估计的概率密度函数之间的欧式距离引入基于区域的主动轮廓模型。文献［53］用对数正态分布来对SAR图像的轮廓内外局部区域建模，然后用Kullback－Leibler散度来度量一对局部区域概率密度之间的差异。

这里需要指出的是，基于区域分布距离［52－53］的主动轮廓模型与前文所述的只考虑区域统计信息［49－51］的主动轮廓模型之间的区别仅仅在于区域拟合能量项的构建方式不同而已：只考虑区域统计信息［49－51］的主动轮廓模型的理论基础是贝叶斯最大后验概率，即依据图像I的一个最优分割P（Ω）可以通过最大后验概率p（P（Ω）｜I）来计算，而最大后验概率又等效于最小化它的负对数［42］，所以这类模型的能量泛函最小化，可以引导轮廓向着最优的分割边界演化。而基于区域分布距离的主动轮廓模型［52－53］的能量泛函的构建方式则很容易理解，因为当实际的区域统计分布与被估计的区域统计分布之间的距离最小时［52］，才表明此时所分割的目标区域与我们所期望的目标区域是吻合的，即轮廓处于最佳的分割位置；或者当轮廓内外局部区域统计分布之间的距离最大时［53］，才表明此时轮廓处于目标和背景的最佳分割位置。

基于区域分布距离的主动轮廓模型之所以比经典的主动轮廓模型（如：GAC、CV等模型）对噪声更鲁棒，在于其采用了恰当的区域统计分布这一先验知识来对SAR图像进行区域统计建模，比如：文献［52］采用shifted－Rayleigh分布来估计具有严重斑点噪声的超声波医学图像的局部区域概率密度，文献［53］则采用对数正态分布对MSTAR和油污等实测SAR图像进行区域统计建模，虽然上述两种主动轮廓模型的能量泛函构建方式不同，但两者都强调了选择合适的统计模型对图像分割性能是至关重要的。下面以文献［52－53］为例，从理论上来分析这类主动轮廓模型的抗噪性能。

文献［52］中对能量泛函的构造如下：

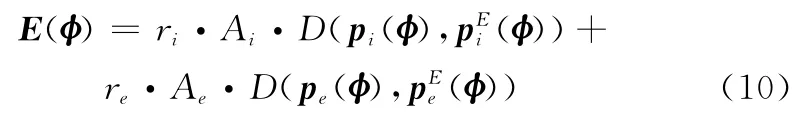
式中，ri和re是两个预先定义的正数；Ai和Ae分别为局部区域Ωi和Ωe的面积；pi和pe分别表示局部区域Ωi和Ωe的实际概率密度函数；和分别表示局部区域Ωi和Ωe的估计概率密度函数。

这种能量泛函的定义有以下两个优点：①预定义的权值ri和re中较大的一个，可以用于增大目标区域（例如Ωi）或背景区域（例如Ωe）的能量变化在整个轮廓演化过程中的重要性；②利用面积Ai和Ae作权值，更强调轮廓的演化在较大的区域中进行，这样更多的像素将被处理得更好。如果没有面积作为权值项（经典的CV模型中没有这种权值项，见式（4）），那么不同大小的区域将被以同等的优先级处理，这样很多小区域将被处理，从而影响了整个轮廓的演化，甚至对噪声比较敏感。但该模型的分割性能非常依赖于用户估计的区域概率密度函数。我们假设当前目标区域Ωi的能量所占的权重较大，那么只有当估计的概率密度函数比较接近于实际概率密度函数pi时，才能保证能量泛函E（φ）的最小化能引导轮廓向着正确的方向演化。

文献［53］所提的主动轮廓模型也是基于区域概率分布函数之间的距离构建的，不同的是，它是基于轮廓内外的局部像素块的概率分布之间距离定义的。

式中，ps和pt分别表示以像素s和t为中心的两个像素块；S和SC分别表示轮廓C的内部和外部区域；d（ps，pt）＝是基于Kullback-Leibler散度定义的像素块ps和pt之间的距离，其中g（z）为描述各像素块概率分布的对数正态分布函数。所以上式的第一项表示轮廓内部区域的能量，第二项表示轮廓外部区域的能量。

文献［53］的主动轮廓模型比较简单，其主要思想就是通过轮廓内外的像素块之间的距离来构建轮廓内外区域的能量函数。显然当轮廓内外的能量都达到最小时，也意味着轮廓内外像素块之间的距离最小，即：轮廓内外区域都趋于同质。当然，这里面同样有两个问题比较关键：一是像素块的概率分布函数的选取是否恰当；二是像素块的尺寸大小的选取是否恰当。前者的正确选取与否，关系到能量函数的计算正确与否，因为不合适的分布函数会导致像素块之间距离计算误差较大，从而影响相应区域的能量泛函的强弱；后者的选取恰当与否，关系到该模型对相干斑噪声鲁棒性的强弱，由于不同的SAR图像的相干斑噪声程度不尽相同，那么像素块的尺寸大小的选取也需要适时改变。

总得来说，只要针对具体的SAR图像进行适当的参数选取，基于区域统计信息的主动轮廓模型比经典主动轮廓模型对SAR图像分割的鲁棒性更强。经典的主动轮廓模型，要么不包含区域统计信息（如基于边缘的snake、GAC等模型），要么仅仅采用简单的局部区域均值来构造区域拟合函数（如CV模型），显然这样的模型是无法在具有相干斑噪声的SAR图像分割中取得满意的效果。

虽然上述两类基于区域统计的模型对噪声都具有一定的鲁棒性，但其对区域的统计建模都是基于先验知识，需要用户先确定区域分布类型，然后用实际的图像数据来估计这些模型的参数，这对用户提出了较高的要求。文献［54］提出了基于信息论的互信息代价函数的主动轮廓模型，该方法不同于一般的基于区域概率密度函数的分割方法，它是一种无参数的概率密度估计方法，不需要任何关于感兴趣区域的先验知识，可以在曲线演化过程中学习区域的概率密度分布。

也有学者提出了仅仅依靠轮廓内外的概率密度函数之间的距离度量的主动轮廓模型。比如：文献［55］用各向同性高斯核函数的核密度估计方法估计区域的概率分布，然后利用Bhattacharyya距离定义了反映轮廓内外区域分布差异的能量泛函。文献［14］基于预测理论计算主动轮廓内外区域中像素概率密度函数之间的距离，文献［56］对文献［14］的分布度量进行了简化。这些用于图像分割的分布度量最小时，可以实现轮廓内部匹配目标，轮廓外部匹配背景，这些方法也被称为基于分布度量的主动轮廓模型［14］。

总之，随着区域统计建模方法的发展，将会出现越来越多的基于区域统计信息的主动轮廓模型，这类模型对含噪的SAR图像分割会更鲁棒，更智能和不需要先验知识的引导。

2.3 基于目标形状先验知识的ACM

如前所述，无论是基于边缘还是基于区域统计信息的主动轮廓模型，其能量泛函的设计都是仅考虑图像中像素的强度信息，这些模型在分割部分被遮挡的目标或者低对比度的图像时将会失效，然而实际应用中会遇到很多这样的情况。为此，出现了很多将目标形状的先验信息加入到主动轮廓模型的方法。

事实上，经典主动轮廓模型的能量泛函一般都带有一个曲线长度惩罚项μ·Length（C）（如式（4）第一项），我们可以将其看作一个先验形状能量项，该项对目标的轮廓演化起到约束作用，该能量项越大，对曲线长度的增长限制作用也越强。当然，如果这里的约束项不仅仅只对曲线长度进行约束，而是采用更复杂的统计分析方法定义先验形状信息，使之对曲线的最终形状也具有约束和引导作用，那么这样所构建的能量泛函最小化将更好地引导轮廓向期望的目标边界演化。实际上，已经有很多加入目标先验形状知识的主动轮廓模型用于图像分割工作［57－65］。

关于形状能量项的定义，很多文献都是基于目标形状训练集的统计分析。比如：文献［57］通过对目标形状集合的主成分分析（principal components analysis，PCA）获取目标的形状变量z∈R2N，并建立了的形状变量的高斯分布P（z），z0表示训练集中各形状变量的均值。然后根据该分布定义了相应的形状能量泛函，并将该形状能量泛函与Mumford-Shah泛函线性加权组合定义了基于形状先验知识的能量泛函：

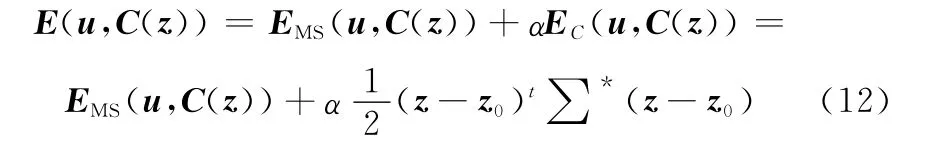
与经典snake模型相比，这种加入目标形状能量的主动轮廓模型具有较强的抗噪性。然而该方法仅考虑了目标的形状，没有考虑目标的姿态。文献［58］通过最大后验概率估计目标训练集的形状和姿态，并将由先验形状知识提供的全局形状力与测地线主动轮廓模型提供的局部图像力（即图像梯度和曲率）相结合组成了新的主动轮廓模型，在具有模糊边界的医学图像器官形状获取上取得了较好的效果。

随着水平集概念的提出，文献［59］提出用符号距离函数来表示目标形状。文献［60］采用Paragios的形状表示方法，并且引入了一个动态标记函数来限制形状先验知识在图像中的作用区域，由此定义了新的形状能量项。

然而上述文献对目标形状的描述都是基于固定形状，没有考虑平移、旋转、缩放对目标形状先验知识造成的影响。文献［61］将目标形状函数用一个仿射变换的四元组（a，b，r，θ）进行变换，使形状能量项对平移、旋转、缩放保持不变。文献［62］将目标的先验形状用缩放、旋转和平移对应的3个参数进行仿射变换得到相似的形状变量，然后将形状变量与相应水平集函数的距离加入到测地线模型构建了新的能量泛函。由于加入了仿射变换的形状信息，即使整个边界不完全可见，该主动轮廓模型也可以寻找到与先验形状相似的目标边界。

关于目标形状的仿射变换，上述文献都是基于目标形状变量在平面中的仿射变换，主要是通过某些固定的平移、旋转、缩放参数进行变换。文献［66－67］采用黎曼测度对曲线进行参数化描述，这种描述框架将形状分析由非弹性分析转变为弹性分析，更有利于仿射不变特征的形状匹配。后来，文献［63］又根据文献［67］中的形状分析技术定义了仿射不变的弹性形状先验知识，并将其引入到主动轮廓模型，通过对SAR图像目标阴影的分割实验，显示了这种弹性形状知识在SAR图像目标形状匹配中的优势。

由于含有感兴趣目标的SAR图像一般比较稀疏，所以很多参数估计算法不能有效运行［68］。近些年，随着机器学习的发展，出现了一些采用非线性映射来学习目标形状先验知识的方法，这类方法将高维空间非线性映射到低维空间，用较少的数据得到高维图像的低维坐标，大大降低了计算的复杂度并节省存储空间。例如文献［68］对SAR图像目标边缘结构信息进行流形学习，得到了目标形状的低维流形的最少数据点表示。所以，对于稀疏的SAR图像中目标的分割和识别，非线性映射方法将会显著地降低算法的空间复杂度，并提高运算速度。遗憾的是，在SAR图像分割领域，到目前为止，我们还没有发现将流形学习等非线性映射方法得到的形状先验知识融入到主动轮廓模型中，直接进行SAR图像分割的方法。而在医学图像分割中，已有这样的先例。比如：针对目前医学图像的目标边界模糊，不好准确判断的问题，文献［65］用目标边界的局部图像集对多层感知器进行训练，从而能够利用神经网络的非线性映射将已知边界转化为先验知识，在分类阶段利用神经网络将图像分为边界像素和非边界像素两类后，再结合snake模型对这些边界像素点进行连接，进而能够获取目标边界的封闭轮廓，但该方法还无法将神经网络获取的形状知识直接嵌入到主动轮廓模型的能量泛函中；文献［69］采用流形学习将目标先验形状非线性映射为低维的数据，并定义了相应的形状能量泛函，该方法比传统的线性降维方法能更有效地发现高维数据的本质。然而，这些非线性映射方法都需要足够多的目标形状样本来进行训练，以获取更加逼近真实的先验形状知识。所以，训练样本的数量会影响这类模型先验知识的获取。但是，对神经网络来说，太多的训练样本会造成网络的过拟合，反而会影响网络的泛化性能，降低网络的分类能力［70－71］；对流形学习来说，过多的训练样本并不会得到更精确的低维描述，反而会增加计算的复杂度［68］。所以并不是样本越多越好，如何根据实际问题准确把握训练样本的数目，也是个研究热点。

综上所述，基于目标形状先验知识的主动轮廓模型主要可以归结为3大类：第一类是对目标集合进行统计分析，建立形状变量的分布模型，从而定义相应的形状能量项；第二类是用水平集函数来描述目标形状曲线，通过水平集函数之间的距离建立相应的形状能量项；第三类是通过机器学习的非线性映射方法获取形状的先验知识，并定义相应的形状能量泛函。

关于第一类方法，大多数文献都是用统计建模的方式来估计形状分布的参数，但是目前也出现了无参数建模的方法，如文献［72］用Parzen密度估计器来估计形状的分布，文献［73］用核密度估计（kernel density estimation，KDE）来获取目标形状的先验信息，不再需要预先的分布假设，更加符合实际情况；关于第二类方法，采用水平集函数来表示形状曲线的方法正获得越来越多的应用。关于第三类方法，在医学图像分割方面已有这方面的应用，在SAR图像分割领域只有学者通过机器学习获取SAR图像目标形状先验知识，但是将非线性映射和主动轮廓模型优势相结合，实现对SAR图像快速而有效的分割将具有很大的吸引力。然而不管是哪种方法，都正在向鲁棒性方向发展，比如：文献［60－63］对先验形状仿射变换后建立的形状能量泛函增强了对同类目标分割的泛化能力。

2.4 基于像素相似性度量的ACM

在图像去噪、分割或分类中，鲁棒性地描述两个有噪声的像素点之间的相关性很重要。根据像素间的相似性来确定同质区域或目标边界，也可以实现对图像的分割［74］。例如，文献［74］基于图像局部区域间的像素成对相似性和测地核函数定义的连接权函数设计了一种主动轮廓模型，对边界模糊的低对比度光学图像有较好的分割结果。然而对于SAR图像来说，相干斑噪声使原本具有常数后向散射系数的均匀同质区域变得不均匀，出现许多斑点，所以简单使用像素相似性度量无法正确分割出SAR图像中的同质区域。另外，该方法在计算局域像素块之间的相似性时，仍然采用欧氏距离计算，而文献［35］证明了像素块之间的比率距离对乘性相干斑噪声更鲁棒，且能够保持像素真实后向散射系数之间的距离，而传统的欧几里德距离在这种情况下是失效的。2012年，文献［64］已经用非局域窗中的像素块之间的比率距离来度量SAR图像的像素相似性，有效克服了相干斑噪声对像素相似性度量的影响。

基于像素块之间的比率距离进行像素相似性度量，不需要先验分布函数知识，使用起来更加简单易行。图2（a）和图2（b）为之前提出的一种MLGIF主动轮廓模型［75－76］对SAR图像分割的效果图，该模型的创新之处在于采用了轮廓内外区域的分布度量和像素块之间的比率距离对LGIF模型中的区域拟合能量项进行了改进；后来又利用GMAC的凸函数框架对MLGIF模型进行了凸优化，提出了GMLGIF主动轮廓模型［77］，该模型收敛速度更快，且对初始轮廓不敏感，其对SAR图像的分割效果如图2（c）所示。由图2可以看出，采用比率距离的主动轮廓模型对乘性相干斑噪声的鲁棒性更强，分割结果明显优于图1所示的经典主动轮廓模型。今后把这种新的度量方法加入主动轮廓模型以提高其在SAR图像分割中的抗噪性和准确性，将会有更广泛的应用。

为了更加清晰的说明本节所述的基于ACM的SAR图像分割方法及其之间关联，我们将其整理并给出了以下的框图，如图3所示。图3中，“＋”表示方法或模型之间进行组合；限于篇幅，图中所列方法并不一定代表其所属类别的全部方法。

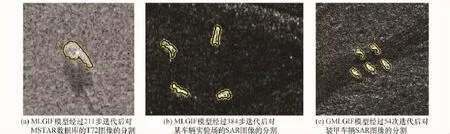
图2 文献［75－77］所提主动轮廓模型对SAR图像的分割

图3 文中基于ACM的SAR图像分割方法的框图

3 基于ACM的SAR图像分割方法展望

不同于传统的光学图像分割方法，基于主动轮廓模型的SAR图像分割方法涉及更多的困难，如：相干斑噪声、模糊的目标边缘、低对比度、非目标强散射点的干扰以及大场景SAR图像的稀疏性。虽然目前已经有学者采用非局域像素块比率距离研究了相干斑噪声下的像素相似性度量，也有学者采用流形学习方法研究了稀疏场景SAR图像的非线性映射，但主动轮廓模型在SAR图像分割中的应用仍有以下问题需要继续探索：

（1）由于SAR的相干成像机理，SAR图像存在固有的相干斑噪声。如何在抗噪性和目标细节保持上都取得好的效果，需要进一步研究类似于比率距离性质的相似性度量，该度量既具有鲁棒的SAR图像像素相关性特征，同时又能保持真实后向散射系数之间的距离。将这种度量引入主动轮廓模型的能量泛函，会使主动轮廓模型更加适合SAR图像分割。

（2）由于传统的基于边缘的主动轮廓模型主要利用梯度信息引导轮廓的演化，所以模型对噪声敏感。虽然经典的基于区域的主动轮廓模型具有一定的抗噪性（如：CV、RSF、LGIF和LGDF等），但这类模型的能量泛函都是非凸函数，所以轮廓易陷入局部极小值，且分割结果对水平集函数的初始值比较敏感。为此，出现了很多以Chan等人提出的GMAC框架为基础的凸优化方法，对非凸模型进行优化，从而解决了非凸模型的全局最小值实现问题。然而，如何根据SAR图像特性，从本质上建立一个凸的能量泛函，更有效、更精确地实现对SAR图像的分割是亟待解决的难题，这需要我们更深入地研究凸优化理论与SAR图像特性相结合的建模方法。

（3）基于区域统计信息的主动轮廓模型，一直是研究的热点。大多数方法都是采用已知分布进行区域统计建模，但需要用户具有相关的先验知识。目前，也出现了一些基于信息论的互信息的非参数建模方法［54］，不需要任何关于感兴趣区域的先验知识。如何在提高建模准确性的同时，降低对先验分布的依赖，仍然具有重要的实际应用价值，值得继续探索。

（4）虽然SAR具有一定的穿透性，但SAR图像中仍不可避免地出现一些目标部分被遮挡或低对比度的现象。目前，已经有学者利用目标形状先验知识将这类目标完整地分割出来，然而由于SAR的侧视成像原理，不同的入射角和方位角使SAR图像中的同类目标轮廓存在一定的变化。为此，目前大多数研究都是对目标先验形状进行仿射变换来获取仿射不变的形状知识，从而使所建立的主动轮廓模型能分割出同类目标。但是，一般仿射变换都是基于固定的变换参数，为了使所定义的先验形状对存在一定变化的同类目标形状的泛化性能更强，有学者将弹性形状分析技术引入到SAR图像目标先验形状知识的获取中，提出了弹性形状先验知识的概念。关于这一技术，目前的研究还不多，所以如何使先验形状知识更具弹性，需要进一步结合已有的形状分析技术；另外，SAR图像目标的阴影也有一定的形状，甚至相比目标与背景来说对比度更高，目前已有单独用目标或阴影的形状进行分割的主动轮廓模型，但是如何有效地将目标和阴影的形状相结合来实现目标分割，在主动轮廓模型中也将是一个重要研究方向。

（5）基于机器学习的主动轮廓模型的研究尚处于起步阶段，目前研究不多。如何结合机器学习的最新研究成果，实现对稀疏的SAR图像中目标边缘结构信息的非线性映射，显著地提升模型的处理速度和分割效果，具有实际意义。另外，如何将机器学习获得的目标低层特征映射为高层知识，并将其引入到主动轮廓模型中的能量泛函，是一个研究难点，也将是主动轮廓模型发展的高级阶段。

4 结束语

乘性相干斑噪声造成经典的主动轮廓模型在SAR图像分割中存在诸多问题，如：抗噪性不佳、对初始轮廓位置敏感以及无法收敛到全局最小值等。本文对经典的主动轮廓模型进行了梳理，并分析了其无法处理SAR图像分割的原因。然后，对目前基于主动轮廓模型的SAR图像分割方法进行了综述，并结合SAR图像的特点对未来的研究方向进行了展望。随着凸优化、统计建模、像素相似性度量和非线性映射等数学理论的不断发展，将有更有效、更快速的算法引入主动轮廓模型，这将使基于主动轮廓模型的SAR图像分割方法有更广阔的应用前景。

［1］Li P H，Zhang T W.Review on active contour model（snake model）［J］.Journal of Software，2000，11（6）：751－757.（李培华，张田文.主动轮廓线模型（蛇模型）综述［J］.软件学报，2000，11（6）：751－757.）

［2］Caselles V，Catte F，Coll T，et al.A geometric model for active contours in image processing［J］.Numerische Mathematic，1993，66（1）：1－31.

［3］Kass M，Witkin A，Terzopoulos D.Snakes：active contour models［J］.International Journal of Computer Vision，1988，1（4）：321－331.

［4］Caselles V，Kimmel R，Sapiro G.Geodesic active contours［J］.International Journal of Computer Vision，1997，22（1）：61－79.

［5］Chan T F，Vese L A.Active contours without edges［J］.IEEE Trans.on Image Processing，2001，10（2）：266－277.

［6］Vese L A，Chan T F.A multiphase level set framework for image segmentation using the mumford and shah model［J］.International Journal of Computer Vision，2002，50（3）：271－293.

［7］Li C，Kao C Y，Gore J C，et al.Implicit active contours driven by local binary fitting energy［C］∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition（CVPR），2007：1－7.

［8］Li C，Kao C Y，Gore J C，et al.Minimization of region-scalable fitting energy for image segmentation［J］.IEEE Trans.on ImageProcessing，2008，17（10）：1940－1949.

［9］Wang L，He L，Mishra A，et al.Active contours driven by local gaussian distribution fitting energy［J］.Signal Processing，2009，89（12）：2435－2447.

［10］Wang L，Li C，Sun Q，et al.Active contours driven by local and global intensity fitting energy with application to brain MR image segmentation［J］.Computerized Medical Imaging and Graphics，2009，33（7）：520－531.

［11］Lecellier F，Fadili J，Jehan-Besson S，et al.Region-based active contours with exponential family observations［J］.Journal of Mathematical Imaging and Vision，2010，36（1）：28－45.

［12］Feng J，Cao Z，Pi Y.Multiphase SAR image segmentation with G0-statistical-model-based active contours［J］.IEEE Trans.on Geoscience and Remote Sensing，2013，51（7）：4190－4199.

［13］Lankton S，Nain D，Yezzi A，et al.Hybrid geodesic regionbased curve evolutions for image segmentation［C］∥Proc.of the SPIE6510，Medical Imaging：Physics of Medical Imaging，2007.

［14］Sandhu R，Georgiou T，Tannenbaum A.A new distribution metric for image segmentation［C］∥Proc.of the SPIE6914，Medical Imaging：Image Processing，2008.

［15］Chen B，Lai J H.Active contour models on image segmentation：a survey［J］.Journal of Image and Graphics，2007，12（1）：11－20.（陈波，赖剑煌.用于图像分割的活动轮廓模型综述［J］.中国图象图形学报，2007，12（1）：11－20.）

［16］Cremers D，Rousson M，Deriche R.A review of statistical approaches to level set segmentation：integrating color，texture，motion and shape［J］.International Journal of Computer Vision，2007，72（2）：195－215.

［17］Wang F M，Fan H，Wang F N.Survey on application of level set in image segmentation［J］.Application Research of Computers，2012，29（4）：1207－1210.（王芳梅，范虹，王凤妮.水平集在图像分割中的应用研究［J］.计算机应用研究，2012，29（4）：1207－1210.）

［18］Qian Y，Zhang Y J.Level set methods and its application on image segmentation［J］.Journal of Image and Graphics，2008，13（1）：7－13.（钱芸，张英杰.水平集的图像分割方法综述［J］.中国图象图形学报，2008，13（1）：7－13.）

［19］Tian Y，Zhou M Q，Duan F Q，et al.Efficient active contour model driven by statistical and gradient information［J］.Journal of Image and Graphics，2011，16（8）：1489－1496.（田沄，周明全，段福庆，等.结合统计和梯度信息的高效活动轮廓模型［J］.中国图象图形学报，2011，16（8）：1489－1496.）

［20］Tian Y，Duan F Q，Zhou M Q，et al.Active contour model combining region and edge information［J］.Machine Vision and Applications，2013，24（1）：47－61.

［21］SunY G，Cai C，Zhou C P，et al.R-Snake：A snake model using both boundary and region information［J］.Acta Electronica Sinica，2009，37（8）：1810－1815.（孙阳光，蔡超，周成平，等.R-Snake：一种基于边缘与区域信息的图像主动轮廓提取模型［J］.电子学报，2009，37（8）：1810－1815.）

［22］Appia V，Yezzi A.Active geodesics：region-based active con-tour segmentation with a global edge-based constraint［C］∥Proc.of the 13th IEEE International Conference on Computer Vision（ICCV），2011：1975－1980.

［23］Chakraborty A，Duncan J S.Game-theoretic integration for image segmentation［J］.IEEE Trans.on Pattern Analysis and Machine Intelligence，1999，21（1）：12－30.

［24］Feng C L，Zhang J X，Dai Y.A relay active contour model for image segmentation based on edge and region information［J］.Chinese High Technology Letters，2013，23（4）：421－429.（冯昌利，张建勋，代煜.基于边缘和区域信息的接力型活动轮廓图像分割模型［J］.高技术通讯，2013，23（4）：421－429.）［25］Cohen L D.On active contour models and balloons［J］.Computer Vision，Graphics，and Image Processing：Image Understanding，1991，53（2）：211－218.

［26］Ge X，Tian J.An automatic active contour model for multiple objects［C］∥Proc.of the 16th International Conference on Pattern Recognition，2002：881－884.

［27］Saha B N，Ray N，Zhang H.Automating snakes for multiple objects detection［J］.Lecture Notes in Computer Science，2011，6494：39－51.

［28］Nixon M S，Aguado A S.Feature extraction and image processing［M］.2nd ed.London：Academic Press，2008：241－261.

［29］Osher S，Sethian J A.Fronts propagating with curvature dependent speed：algorithms based on the Hamilton-Jacobi formulation［J］.Journal of Computational Physics，1988，79：12－49.

［30］Feng J L，Cao Z J，Pi Y M.A global stationary minimum level set segmentation method for high-resolution SAR images［J］.Journal of Electronics ＆Information Technology，2010，32（11）：2618－2623.（冯籍澜，曹宗杰，皮亦鸣.适用于高分辨SAR图像的全局稳态最小水平集分割方法［J］.电子与信息学报，2010，32（11）：2618－2623.）

［31］Chan T F，Esedoglu S，Nikolova M.Algorithms for finding global minimizes of image segmentation and denoising models［J］.Society for Industrial and Applied Mathematics（SIAM）Journal on Applied Mathematics，2006，66（5）：1632－1648.

［32］Mumford D，Shah J.Optimal approximation by piecewise smooth functions and associated variational problems［J］.Communication on Pure and Applied Mathematics，1989，42：577－685.

［33］Ambrosio L，Tortorelli V.Approximation of functionals depending on jumps by elliptic functionals via-convergence［J］.Communication on Pure and Applied Mathematics，1990，43：999－1036.

［34］Chambolle A.Finite-difference discretizations of the Mumford-Shah functional［J］.Mathenatics Modeling and Numerical A-nalysis，1999，33（2）：261－288.

［35］Feng H，Hou B，Gong M.SAR image despeckling based on local homogeneous-region segmentation by using pixel-relativity measurement［J］.IEEE Trans.on Geoscience and Remote Sensing，2011，49（7）：2724－2737.

［36］Xu X，He C.Implicit active contour model with local and global intensity fitting energies［J］.Mathematical Problems in Engineering，2013，Article ID367086，13 pages.http：∥dx.doi.org／10.1155／2013／367086.

［37］Wu B，Yang Y.Local-and global-statistics-based active contour model for image segmentation［J］.Mathematical Problems in Engineering，2012，Article ID791958.http：∥dx.doi.org／10.1155／2012／791958.

［38］Yao C，Zhang J，Chen M，et al.Incorporating a local binary fitting model into a maximum regional difference model for extracting microscopic information under complex conditions［J］.Mathematical Problems in Engineering，2012，Article ID474938.http：∥dx.doi.org／10.1155／2012／474938.

［39］Zhang K，Zhang L，Song H.Active contours with selective local or global segmentation：a new formulation and level set method［J］.Image and Vision Computing，2010，28（4）：668－676.

［40］He Z G.SAR image segmentation based on the active contour model［D］.Changsha：National University of Defense Technology，2008：13－14，22－23，49－50，85－86.（贺志国.基于活动轮廓模型的SAR图像分割算法研究［D］.长沙：国防科学技术大学，2008：13－14，22－23，49－50，85－86.）

［41］Song H，Huang B，Zhang K.A globally statistical active contour model for segmentation of oil slick in SAR imagery［J］.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2013，6（6）：1－8.

［42］Zhu S C，Yuille A.Region competition：Unifying snakes，region growing，and Bayes／MDL for multiband image segmentation［J］.IEEE Trans.on Pattern Analysis and Machine Intelligence，1996，18（9）：884－900.

［43］Bresson X，Esedoglu S，Vandergheynst P，et al.Fast global minimization of the active contour／snake model［J］.Journal of Mathematical Imaging and Vision，2007，28：151－167.

［44］Rudin L I，Osher S，Fatemi E.Nonlinear total variation based noise removal algorithms［J］.Physica D：Nonlinear Phenomena，1992，60（1／4）：259－268.

［45］Jing Y，An J，Liu Z.A novel edge detection algorithm based on global minimization active contour model for oil slick infrared aerial image［J］.IEEE Trans.on Geoscience and Remote Sensing，2011，49（6）：2005－2013.

［46］Tao Z，Tagare H D.Tunneling descent for m.a.p.active contours in ultrasound segmentation［J］.Medical Image Analysis，2007，11（3）：266－281.

［47］Lee S H，Seo J K.Level set-based bimodal segmentation with stationary global minimum［J］.IEEE Trans.on Image Processing，2006，15（9）：2843－2852.

［48］Li C，Xu C，Gui C，et al.Level set evolution without re-initialization：a new variational formulation［C］∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition，2005：430－436.

［49］Wu Q，An J，Lin B.A texture segmentation algorithm based on PCA and global minimization active contour model for aerial insulator images［J］.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2012，5（5）：1509－1518.

［50］Achuthan A，Rajeswari M，Ramachandram D，et al.Wavelet energy－guided level set-based active contour：a segmentation method to segment highly similar regions［J］.Computers in Bi-ology and Medicine，2010，40（7）：608－620.

［51］Shyu K K，Tran T T，Pham V T，et al.Fuzzy distribution fitting energy-based active contours for image segmentation［J］.Nonlinear Dynamics，2012，69（1／2）：295－312.

［52］Liu B，Cheng H.D，Huang J，et al.Probability density differencebased active contour for ultrasound image segmentation［J］.Pattern Recognition，2010，43（6）：2028－2042.

［53］Liu G，Xia G S，Yang W，et al.SAR image segmentation via non-local active contours［C］∥Proc.of the IEEE International Geoscience and Remote Sensing Symposium（IGARSS），2014：3730－3733.

［54］Kim J，Fisher III J W，Cetin M，et al.Incorporating complex statistical information in active contour-based image segmentation［C］∥Proc.of the International Conference on Image Processing，2003：655－658.

［55］Michailovich O，Rathi Y，Tannenbaum A.Image segmentation using active contours driven by the Bhattacharyyagradient flow［J］.IEEE Trans.on Image Processing，2007，16（11）：2787－2801.

［56］Peng S J，Liu X，Cheung Y.Active contours with a novel distribution metric for complex object segmentation［C］∥Proc.of the 18th IEEE International Conference on Image Processing，2011：3345－3348.

［57］Cremers D，Schnorr C，Weickert J，et al.Diffusion-Snakes Using Statistical Shape Knowledge［J］.Lecture Notes in Computer Science，2000，1888：164－174.

［58］Leventon M E，Grimson W E L，Faugeras O.Statistical shape influence in geodesic active contours［C］∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition（CVPR），2000：316－323.

［59］Paragios N，Rousson M，Ramesh V.Matching distance functions：a shape-to-area variational approach for global-to-local registration［J］.Lecture Notes in Computer Science，2002，2351：775－789.

［60］Cremers D，Sochen N，Schnorr C.Towards recognition-based variational segmentation using shape priors and dynamic labeling［J］.Lecture Notes in Computer Science，2003：388－400.

［61］Chan T，Zhu W.Level set based shape prior segmentation［C］∥Proc.of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition（CVPR），2005：1164－1170.

［62］Chen Y，Tagare H D.Using prior shapes in geometric active contours in a variational framework［J］.International Journal of Computer Vision，2002，50（3）：315－328.

［63］Bryner D，Srivastava A.Shadow segmentation in SAS and SAR using bayesian elastic contours［C］∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition Workshops（CVPRW），2013：375－380.

［64］Li G T，Huang P P，Yu W D.Non-local SAR image despeckling based on similar pixels selected［J］.Journal of Radars，2012，1（2）：171－181.（李光廷，黄平平，禹卫东.基于相似像素选择的非局域SAR图像相干斑抑制［J］.雷达学报，2012，1（2）：171－181.）

［65］Middleton I，Damper R I.Segmentation of magnetic resonance images using a combination of neural networks and active con-tour models［J］.Medical Engineering ＆Physics，2004，26：71－86.

［66］Srivastava A，Klassen E，Joshi S H，et al.Shape analysis of elastic curves in euclidean spaces［J］.IEEE Trans.on Pattern Analysis and Machine Intelligence，2011，33（7）：1415－1428.

［67］Bryner D，Klassen E，Srivastava A.Affine-invariant，elastic shape analysis of planar contours［C］∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition（CVPR），2012：390－397.

［68］Wang W，Bi D Y，Xiong L，et al.SAR image recognition based on sparse manifold learning［J］.Acta Electronica Sinica，2010，38（11）：2540－2544.（王伟，毕笃彦，熊磊，等.基于稀疏流形学习的SAR图像识别［J］.电子学报，2010，38（11）：2540－2544.）

［69］Etyngier P，Segonne F，Keriven R.Active-contour-based image segmentation using machine learning techniques［J］.Lecture Notes in Computer Science，2007，4791：891－899.

［70］Nuchiitprasittichai A，Cremaschi S.An algorithm to determine sample sizes for optimization with artificial neural networks［J］.AIChE Journal，2013，59（3）：805－812.

［71］Xu C，Xu C.Optimization analysis of dynamic sample number and hidden layer node number based on BP neural network［J］.Advances in Intelligent Systems and Computing，2013，212：687－695.

［72］Kim J，Cetinb M，Willsky A S.Nonparametric shape priors for active contour-based image segmentation［J］.Signal Processing，2007，87（12）：3021－3044.

［73］Wang B，Li J，Gao X B.An edge and region-based level set method with shape priors for image segmentation［J］.Chinese Journal of Computers，2012，35（5）：1067－1072.（王斌，李洁，高新波.一种基于边缘与区域信息的先验水平集图像分割方法［J］.计算机学报，2012，35（5）：1067－1072.）

［74］Kong D K，Wang G Z.Localized graph-cuts based multiphase active contour model for image segmentation［J］.Journal of E-lectronics ＆Information Technology，2010，32（9）：2126－2132.（孔丁科，汪国昭.基于局部图划分的多相活动轮廓图像分割模型［J］.电子与信息学报，2010，32（9）：2126－2132.）［75］Tu S，Li Y，Su Y.Ratio-and distribution-metric-based active contours for SAR image segmentation［C］∥Proc.of the 5th International Conference on Intelligent Control and Information Processing，2014：227－232.

［76］Tu S，Li Y，Su Y.A novel scheme of unsupervised target detection for high-resolution SAR image［C］∥Proc.of the 12th the IEEE International Conference on Signal Processing，2014：1000－1005.

［77］Tu S，Su Y，Li Y.Convex active contour model for target detection in synthetic aperture radar images［J］.Journal of Applied Remote Sensing，2015，9（1）：095084.

Overview of SAR image segmentation based on active contour model

TU Song，LI Yu，SU Yi
（School of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China）

Recently，agreat number of interests have been attracted to image segmentation methods based on the active contour model（ACM）.The classical ACM and synthetic aperture radar（SAR）image segmentation methods based on the ACM are reviewed.Firstly，classical ACMs and mathematical principles of them are introduced，and the defects are analyzed when they are applied to SAR image segmentation.Secondly，classified discussion and analysis of SAR image segmentation methods based on the ACM are given.Finally，several future research directions for SAR image segmentations based on the ACM are discussed.

synthetic aperture radar（SAR）image segmentation；active contour model（ACM）；statistical model；convex optimization；similarity metric

TN 957.52

10.3969／j.issn.1001-506X.2015.08.07

涂松（1983－），男，博士研究生，主要研究方向为遥感信息处理、SAR图像解译。

E-mail：song＿tu＠126.com

李禹（1975－），男，博士，副教授，主要研究方向为遥感信息处理、SAR图像解译。

E-mail：liyu4534＠yahoo.com.cn

粟毅（1961－），男，教授，博士研究生导师，博士，主要研究方向为超宽带雷达系统、信号与信息处理、SAR图像解译。

E-mail：suyi1961＠nudt.edu.cn

1001－506X201508－1754－13

网址：www.sys－ele.com

2014－06－26；