由三角范畴的Recollement构造其心范畴的Recollement

许燕青

（厦门大学数学科学学院，福建厦门361005）

由三角范畴的Recollement构造其心范畴的Recollement

许燕青

（厦门大学数学科学学院，福建厦门361005）

Nakaoka利用三角范畴上的余绕对构造出了Abel范畴，这推广了t-结构的心范畴以及关于cluster倾斜子范畴的商范畴的两种情形.之后，Nakaoka又将此结果推广至更一般的关于双余绕对的情形.本文通过考虑双余绕对，由三角范畴的recollement构造出了其心范畴的recollement，它推广了关于余绕对的相关结果.

三角范畴；余绕对；双余绕对；心范畴；recollement

1 预备知识

三角范畴的概念起源于代数几何，1982年，Beilinson等［1］在研究奇异空间时引入了三角范畴的recollement的概念，recollement描述了一个范畴由两个范畴粘合而成的思想.Abel范畴和三角范畴的recollement是数学研究的基本工具，在奇异空间，代数表示论，环论，多项式函子理论，拓扑空间理论等领域起着重要的作用.本文通过考虑Nakaoka引入的双余绕对的概念，由三角范畴的recollement构造其心范畴的recollement，这是陈健敏关于余绕对和林亚南关于cluster倾斜子范畴的研究成果的一个推广［2-3］.本文的主要结论是：

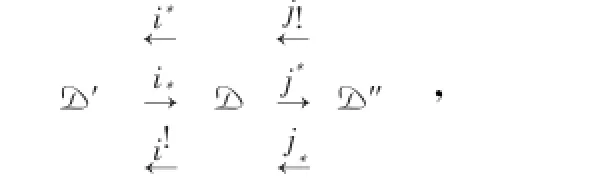
在本文中，三角范畴的shift函子记为［1］，对于给定的三角范畴D，记Ext1（M，N）∶=Hom（M，N［1］），其中M，N∈D，设U，V为D的满子范畴，U*V表示由U和V三角扩张而成的D的加法子范畴，即U *V∶={D∈D｜U→D→V→U［1］，U∈U，V∈V}·

设C是加法范畴，W是C的加法满子范畴，则C/ W表示C关于W的商范畴．其商范畴是加法范畴，且存在加法典范函子Q：C→C/W，它具有泛性：对任意满足F（W）=0的加法函子存在唯一的加法函子使得

其中·如果W对直和项封闭，我们称W为C的thick子范畴.

1）D∈U当且仅当Ext1（D，V）=0；

2）D∈V当且仅当Ext1（U，D）=0；

3）D=U*V［1］.

注1 如果U和V是D的thick子范畴，则（U，V）是余绕对当且仅当（U，V［1］）是文献［4］中的绕对，即满足Ext1（U，V）=0和D=U*V［1］·

Ext1（S，V）=0·

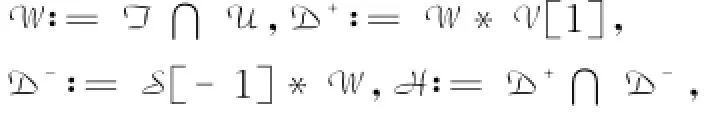
范

畴［］.

2 三角范畴的recollement和双余绕对

首先我们回顾一下加法范畴和三角范畴的recollement的定义.

定义4 设B，B′和B″是加法范畴，则B允许有关于B′和B″的reeollement，记

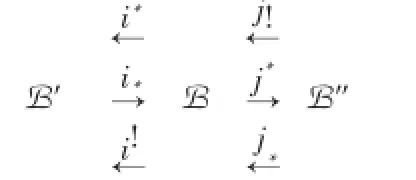
是指6个加法函子

满足以下条件：

1）（i*，i*），（i*，i！），（j！，j*）和（j*，j*）是伴随对；

2）i*，j！和j*是满嵌入函子；

3）j*i*=0·

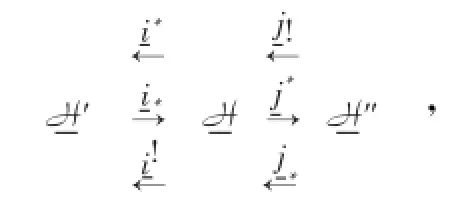
如果B，B′和B″是Abel范畴，则这也可作为A-bel范畴的recollement的定义［7］.下面引入三角范畴的recollement的定义［1］.

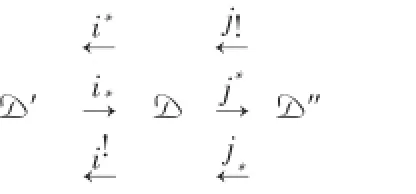
是指6个正合函子，

满足以下条件：

1）（i*，i*），（i*，i！），（j！，j*）和（j*，j*）是伴随对；

2）i*，j！和j*是满嵌入函子；

3）j*i*=0（可推出i*j！=0和i！j*=0）；

4）对任意D∈D，可以确定D的两个好三角i*i！D→D→j*j！D→（i*i！D）［1］和j！j*D→D→i！i*D→（j！j*D）［1］，其中i*i！D→D，D→j*j！D，j！j*D→D和D→i！i*D是相应的连接态射·

注2 在定义4和5中，我们有i*i*≅id，i！i*≅id，j*j*≅id和j*j！≅id·事实上，我们有下面一个引理·

考虑到双余绕对的定义，由文献［2］中关于余绕对的定理3.3和3.4，容易得到关于双余绕对的类似结果：

命题1 设D，D′和D″是三角范畴，D允许有关于D′和D″的recollement

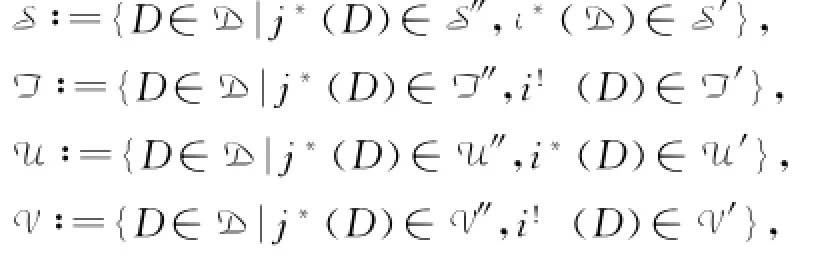
则有：

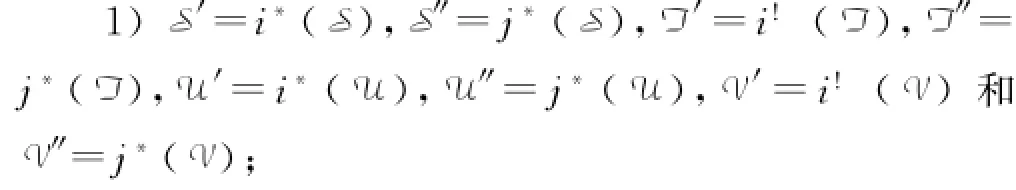
3 心范畴的recollement的构造

定义6 设C和D是三角范畴，（S1，J1），（U1，V1）和（S2，J2），（U2，V2）分别是C和D的双余绕对．正合函子F：C→D称为：

1）左dd-正合如果F（J1）⊆J2和F（V1）⊆V2；

2）右dd-正合如果F（S1）⊆S2和F（U1）⊆U2；

3）dd-正合如果F既是左dd-正合又是右dd-正合.

引理2 设C和D是加法范畴，函子F：C→D伴随于函子G：D→C·令U和V分别是C和D的加法满子范畴，使得F（U）⊆V，G（V）⊆U，则有：

［1］ Beilinson A，Bernstein J，Deligne P.Faisceaux pervers［J］.Soc Math France，1982，100：1-172.

［2］ Chen J.Cotorsion pairs in a recollement of triangulated categories［J］.Communications in Algebra，2013，41：2903-2915.

［3］ Lin Y，Wang M.From recollement of triangulated categories to recollement of abelian categories［J］.Science China Mathematics，2010，53：1111-1116.

［4］ Iyama O，Yoshino Y.Mutation in triangulated categoryies and rigid Cohen-Macaulay modules invent［J］.Math，2008，172：117-168.

［5］ Nakaoka H.General heart construction on a triangulated category：unifying t-structures and cluster tilting subcategories［J］.Appl Categ Structures，2011，19：879-899.

［6］ Nakaoka H.General heart construction for twin torsion pairs on triangulated categories［J］.Journal of Algebra，2013，374：195-215.

［7］ Chen Q，Zheng M.Recollements of abelian categories and special types of comma categories［J］.Journal of Algebra，2009，321：2474-2485.

From Recollement of Triangulated Categories to Recollement of the Heart Categories

XU Yan-qing
（School of Mathematical Sciences，Xiamen University，Xiamen 361005，China）

In the paper of Nakaoka，he constructed an Abelian category from a cotorsion pair on a triangulated category.The resulting Abelian category generalizes the of a t-structure and the quotient a cluster tilting subcategory.After that，Nakaoka generalized these results to a more general setting called twin cotorsion pair.In this article，we construct recollement of the heart categories from a recollement of triangulated categories by considering twin cortorsion pair.It generalized the results about cotorsion pair.

triangulated category；cotorsion pair；twin cotorsion pair；heart category；recollement

O 154.1

A

0438-0479（2015）04-0493-04

10.6043/j.issn.0438-0479.2015.04.009

2014-12-04 录用日期：2015-01-08

Email：452115535＠qq.com

许燕青.由三角范畴的Recollement构造其心范畴的Recollement［J］.厦门大学学报：自然科学版，2015，54（4）：493-496.

：Xu Yanqing.From recollement of triangulated categories to recollement of the heart categories［J］.Journal of Xiamen University：Natural Science，2015，54（4）：493-496.（in Chinese）