考虑周期性波动因素的中长期空中交通流量预测

陈 丹， 胡明华， 张洪海， 尹嘉男

(南京航空航天大学民航学院，江苏南京 211106)

随着我国航空运输业的飞速发展，空中交通流量不断增长，自2006年至今已增长70%左右，年平均增长率达到9%，且未来20年仍将继续保持迅猛增长趋势[1].不断增长的空中交通需求与有限的空域运行能力之间的不平衡状况日趋凸显，空域拥挤与航班延误等问题频发，为进一步提升民航服务品质，有必要对中长期空中交通流量的总体增长趋势和周期性波动规律进行准确预测，这是实施空中交通流量管理的前提和基础，也是空域管理科学决策的重要依据.

中长期空中交通流量预测的常用方法为时间序列预测法，主要包括序时平均数法、指数平滑法、移动平均法、趋势预测法等[2-6].这些方法具有输入数据少、计算量小等特点，但要求时间序列具有稳定性，对于非平稳时间序列，则需通过差分、取对数等方法进行适当的预处理，将其转换为平稳时间序列，但预处理过程可能造成某些重要信息的丢失，降低预测精度[7].

为分析恶劣天气、重大事件等不确定性因素对空中交通流量的影响，将动态线性模型引入空中交通流量预测领域，该模型不要求时间序列平稳性假设，且可用贝叶斯统计方法求解，不仅可预测未来发展趋势，还能给出相应的预测置信区间[8-11].

当前预测方法未考虑气候、季节、交通需求等周期性波动因素对空中交通流量的影响[12].本文综合考虑气候、季节、交通需求等周期性波动因素对空中交通流量的影响，通过分析历史运行数据，分析空中交通流量中长期总体变化趋势和周期性波动规律，建立考虑周期性波动因素的改进动态线性模型，用于预测未来某时空范围内的空中交通流量，为战略流量管理决策提供数据支持.

1 预测模型

1.1 一般动态线性模型

动态线性模型是一种特殊的状态空间模型，也称为高斯线性状态空间模型.假设时刻t=0动态线性模型的初始p维状态向量X0服从先验正态分布，m0为期望，C0为方差，

式中:Yt为时刻t空域单元的m维交通流量向量;

Xt为时刻t交通流的隐含状态;

Ft为状态向量与观测向量之间的映射关系矩阵;

Gt为相邻状态向量之间的映射关系矩阵;

vt(t≥1)和 wt(t≥1)分别为为均值为 0 的方差矩阵Vt(t≥1)和 Wt(t≥1)的独立的高斯随机向量，用于描述观测噪声和过程噪声.

通常将式(2)称为观测方程，式(3)称为状态方程，式(1)～(3)循环递推，构成动态线性模型[13].

1.2 线性增长模型

结合空中交通流量预测问题的特点，本文选取一种特殊的动态线性模型，即线性增长模型[13].此时，m=1，p=2，在标准模型的基础上，增加了状态μt的动态斜率βt，模型参数如下:

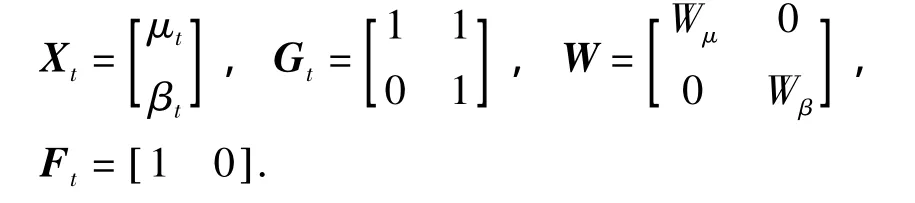
对于中长期空中交通流量预测，μt表示对实际交通流量观测时序数据的估计状态，βt表示该状态的变化率，σμ、σβ为方差，当 m=1、p=2时，线性增长模型为

1.3 周期性波动模型

综合考虑气候、季节、交通需求等周期性波动因素的影响，建立改进模型.假设时序数据的均值为0，即时序数据只存在周期性波动.对于均值非0的时序数据，其变化趋势项可由1.2节构建的线性增长模型预测得到.设波动周期为s，则周期性波动模型(m=1，p=s)的参数如下:

Xt为(s－1)维状态向量(波动周期为s的周期性波动模型，仅有s－1个自由状态);

Ft和 Gt为1×(s－1)维和(s－1)×(s－1)维矩阵;

W为1×(s－1)维矩阵，表示过程噪声.

1.4 预测精度指标

为评价模型预测值与实际值拟合程度的优劣，本文选取两个预测精度指标，即平均绝对误差百分比EMAPE和相对均方根误差百分比ER-RMPSE.这两个指标广泛用于空中交通预测研究[14]，

式中:yt为时刻t的实际观测值;

et为时刻t实际观测值yt与预测期望值ft之间的偏差.

由于中长期流量预测结果对战略流量管理具有重要指导意义，因此，要求预测误差具有较好的稳定性.在统计学中，常用标准差衡量数组之间的离散程度，标准差越小，表示数据越聚集，稳定性越好，反之数据越离散，稳定性越差.本文选用预测误差的标准差η作为评价预测性能稳定性的指标，

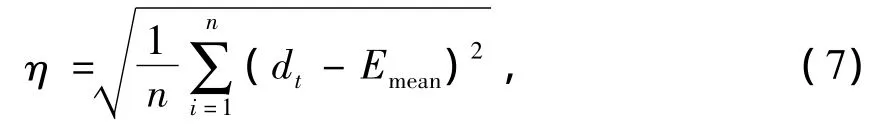
式中:di为时刻t预测结果的相对误差;

Emean为各时刻预测结果相对误差的平均值.

2 预测流程

根据所建模型及求解方法，采用统计分析与计算领域常用的R语言编程工具，对本文提出的预测方法进行算法实现，具体步骤如下:

(1)分析中长期空中交通流量预测的各类动静态影响因素影响，提炼出具备周期性波动特点的因素;

(2)建立考虑周期性波动因素的中长期空中交通流量预测模型，应用基于贝叶斯状态估计与预测理论的方法求解;

(3)读入典型繁忙地区某空域单元在特定时间范围内的历史流量观测时序数据，并建立观测向量Yt;

(4)确定模型参数Gt、Ft以及波动周期s的值，其中线性增长模型的Gt和Ft见1.2节，改进模型的Gt和Ft见1.3节，波动周期s则取决于用于预测的观测数据的时间粒度，例如，月交通流量预测模型中波动周期s=12，季度交通流量预测模型中波动周期s=4;

(5)编程设计R语言程序，对中长期空中交通流量进行预测，并输出预测结果;

(6)对预测结果进行综合对比，并分析本文方法的预测精度.

3 预测实例

选取某地区2001—2010年交通流量数据作为观测数据，应用线性增长模型和考虑周期性波动因素的改进模型对历史交通流量时序数据建模，并采用贝叶斯状态估计与预测方法[15]对模型进行求解，预测未来两年该地区的月交通流量、季度交通流量以及年交通流量，并将预测结果与该地区2011—2012年实际观测数据进行对比分析.

3.1 月交通流量预测

根据某地区2001年1月至2010年12月的月交通流量时序数据，利用1.2节建立的线性增长模型描述该时序数据，采用贝叶斯状态估计和预测方法对该模型求解，预测该地区2011年1月至2012年12月的月交通流量时序数据的未来发展趋势.预测结果如图1所示.

图1 线性增长模型的月交通流量预测结果Fig.1 Monthly traffic flow forecasted by the linear growth model

如图1所示为根据2001—2010年的月交通流量观测数据对未来流量变化趋势的预测情况.假设观测噪声和过程噪声均为高斯噪声，由贝叶斯状态估计与预测理论可知，历史观测时序数据的预测值同样服从高斯分布(图1)，图1中浅色灰线表示20个预测样本.

图1中，实际时序数据具有明显的周期性波动，但线性增长模型只考虑了时序数据的线性发展趋势，预测结果为一条上升的直线，无法体现时序数据的波动性.因此，在线性增长模型的基础上，考虑周期性波动因素，将线性增长模型作为预测趋势项，将周期性波动模型作为波动项，二者相加得到改进的预测模型，预测结果见图2(s=12).

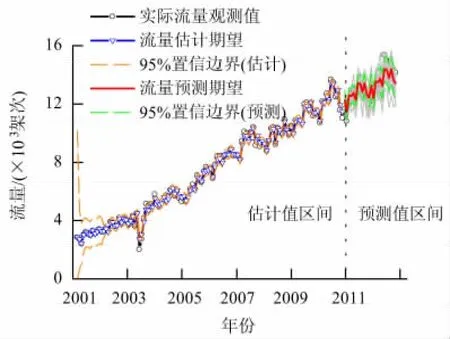
图2 改进模型的月交通流量预测结果Fig.2 Monthly traffic flow forecasted by the improved model

由图2可见，基于改进模型的月交通流量预测结果既能反映时序数据的总体发展趋势，又能较好体现其周期性波动规律，与实际观测时序数据更接近.为直观反映流量数据的波动性对预测结果的影响，将预测结果分解，如图3所示.

图3 改进模型的月交通流量预测结果分解Fig.3 Components of the monthly traffic flow forecasted by the improved model

两组月交通流量预测结果的对比见表1.根据式(5)和(6)可计算得出线性增长模型预测结果的EMAPE和 ER-RMPSE分别为4.00%和5.40%，相对误差的标准差为3.62%;而改进模型预测结果的EMAPE和ER-RMPSE分别为2.62%和3.23%，相对误差的标准差为1.89%，预测精度较线性增长模型明显提高，预测误差也更为稳定.

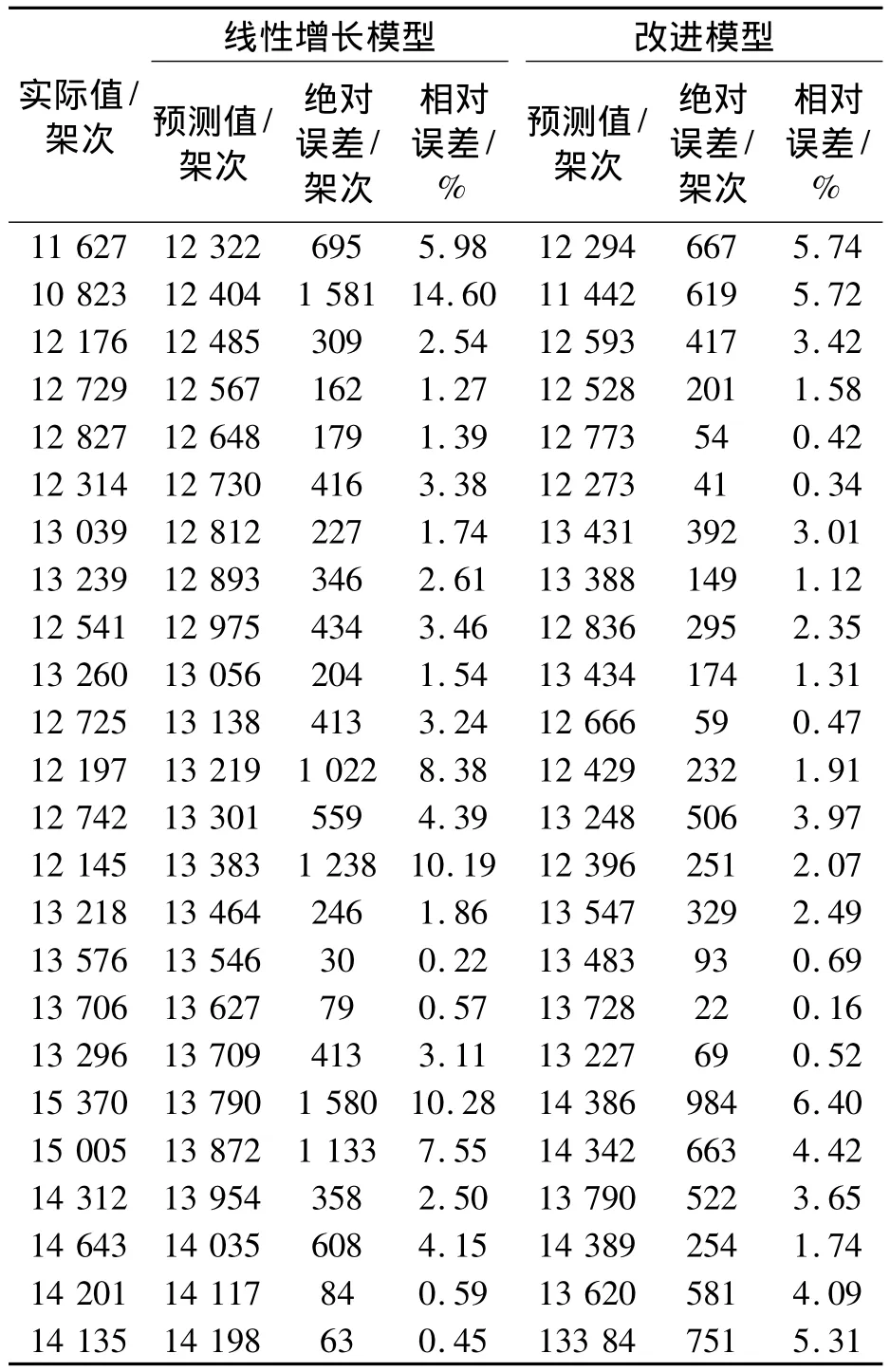
表1 月交通流量预测结果对比Tab.1 Comparison of forecast results of monthly traffic flow between models

3.2 季度交通流量预测

根据2001—2010年的自然季度(春、夏、秋、冬)交通流量时序数据，运用线性增长模型，预测2011—2012年的自然季度交通流量，结果见图4.

图4 线性增长模型的自然季度交通流量预测结果Fig.4 Quarterly traffic flow forecasted by the linear growth model

为准确把握时序数据的客观波动性，采用改进模型对自然季度交通流量进行预测，波动周期s=4，预测结果如图5所示.为更清晰的显示改进模型的预测结果，图6分别给出预测结果的趋势项、波动项以及最终预测结果.

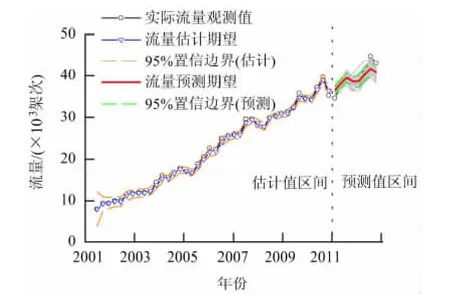
图5 改进模型的自然季度交通流量预测结果Fig.5 Quarterly traffic flow forecasted by the improved model

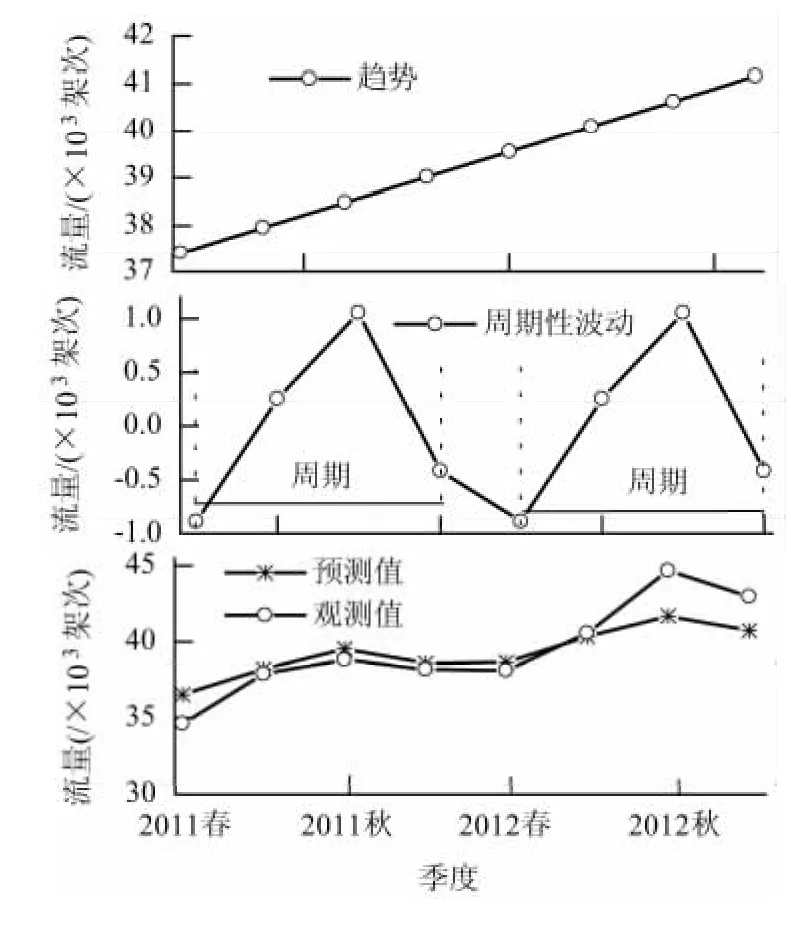
图6 改进模型的自然季度交通流量预测结果分解Fig.6 Components of the quarterly traffic flow forecasted by the improved model

自然季度交通流量预测结果的对比见表2.根据1.4节的预测精度指标公式可计算得出线性增长模型预测结果的EMAPE和ER-RMPSE分别为3.97%和4.94%，相对误差的标准差为2.93%;而改进模型预测结果的 EMAPE和 ER-RMPSE分别为2.91%和3.71%，相对误差的标准差为2.30%，预测精度较线性增长模型略有提高，预测误差也更为稳定.

利用2001年夏秋季(2001年4月至10月)至2009年冬春季(2009年11月至2010年3月)的航班季度(冬春、夏秋)交通流量时序数据，用线性增长模型，预测2010年夏秋季至2012年夏秋季的航班季度交通流量，结果见图7.改进模型航班季度交通流量预测结果见图8.

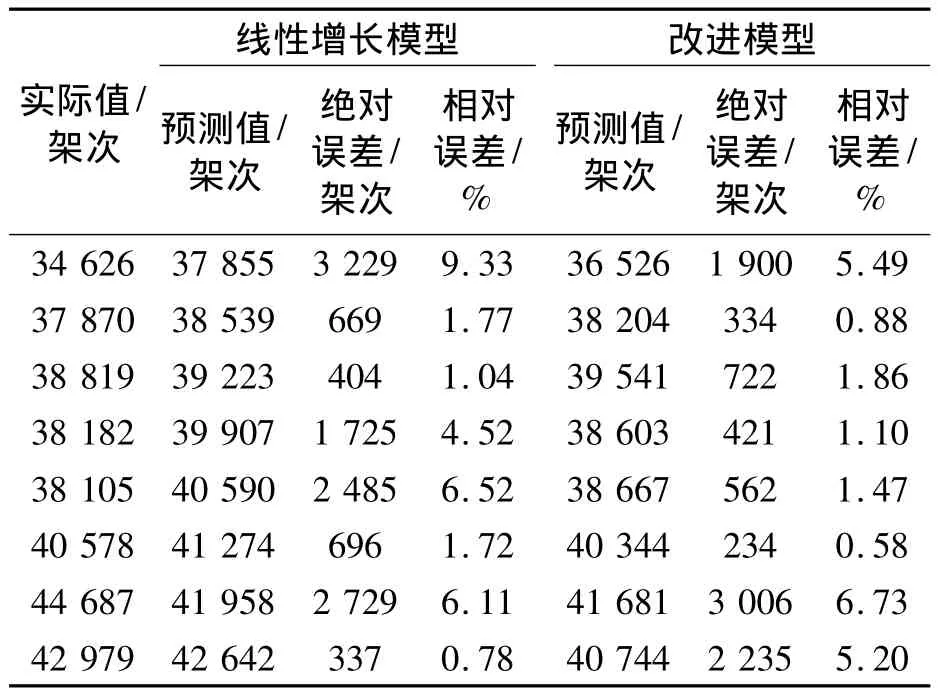
表2 自然季度交通流量预测结果对比Tab.2 Comparison of forecast results of quarterly traffic flow between models

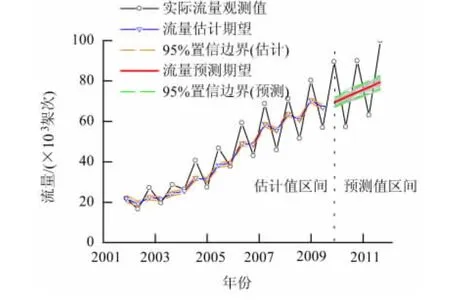
图7 线性增长模型的航班季度交通流量预测结果Fig.7 Traffic flow of flight season forecasted by the linear growth model

图8 改进模型的航班季度交通流量预测结果Fig.8 Traffic flow of flight season forecasted by the improved model

为更清晰地显示改进模型的预测结果，分别给出预测结果的趋势项、波动项以及最终预测结果，如图9所示.

图9 改进模型的航班季度交通流量预测结果分解Fig.9 Components of traffic flow of flight season forecasted by the improved model

两组航班季度交通流量预测结果的对比见表3.

表3 航班季度交通流量预测结果对比Tab.3 Comparison of traffic flow of flight season between models

根据式(5)和(6)可计算得出线性增长模型预测结果的 EMAPE和 ER-RMPSE分别为 21.59%和21.77%，而改进模型预测结果的EMAPE和ER-RMPSE分别为6.23%和6.90%，预测精度较线性增长模型有显著提高.冬春季航班的执行时间为当年10月末至翌年3月末，约5个月，夏秋季航班的执行时间为当年3月末至10月末，约7个月，二者存在2个月的时间差异引起的波动，直接导致不考虑波动性因素的线性增长模型预测结果误差大，此时该模型已不再适用，而改进模型考虑了周期性波动因素，预测结果较好.

3.3 年交通流量预测

根据某地区2001—2010年的年交通流量时序数据，用线性增长模型，预测该地区2011—2012年的年交通流量，结果见图10.

图10 线性增长模型的年交通流量预测结果Fig.10 Yearly traffic flow forecasted by the linear growth model

由于年交通流量时序数据不存在周期性波动规律，本文考虑将基于改进模型的月交通流量预测结果和自然季度交通流量预测结果逐年加和，作为改进模型的年交通流量预测结果.3组年交通流量预测结果的对比见表4.

表4 年交通流量预测结果对比Tab.4 Comparison of yearly traffic flow between models

由表4可知，采用改进模型的两组预测结果误 差要明显小于线性增长模型的预测结果误差，且前者更稳定;由改进模型预测结果可见，与季度交通流量时序数据的预测精度结果相比，月交通流量时序数据的预测精度显著提升.

4 结束语

考虑到实际空中交通流量受气候、季节、交通需求等因素的影响而具有显著的周期性波动特点，

本文在一般动态线性模型的基础上，建立了考虑周期性波动因素的改进模型用于中长期空中交通流量预测，并借助贝叶斯状态估计与预测方法求解模型.实例分析表明，改进模型不仅能够反映空中交通流量中长期的总体变化趋势，而且能够体现交通流量的周期性波动规律，因此，得到更为合理的预测结果，且相较于现有的未考虑周期性波动时序模型(例如线性增长模型)具有更高的预测精度和稳定性.算例结果表明，本文方法适用于中长期时间范围内特定空域单元空中交通流量预测.

[1]中国民用航空局发展计划司.从统计看民航2013[M].北京:中国民航出版社，2013:126-147.

[2]赵玉环，石新华.基于时间序列的空中交通流量灰预测模型算法[J].中国民航大学学报，2007，25(6):54-57.Z

HAO Yuhuan，SHI Xinhua.Air traffic flow gray forecast model algorithm based on time series[J].Journal of China Civil Aviation University， 2007，25(6):54-57.

[3]姜静逸，韩松臣，王玉婷.新型组合预测模型在空中交通流量预测的应用[J].中国民航大学学报，2009，27(5):4-8.

JIANG Jingyi，HAN Songchen，WANG Yuting.New combination forecast model in the application of air traffic flow prediction[J]. JournalofChina Civil Aviation University，2009，27(5):4-8.

[4]ÖNDER E，KUZU S.Forecasting air traffic volumes using smoothing techniques[J].Journal of Aeronautics and Space Technologies，2014，7(1):65-70.

[5]赵玉环，郭爽.考虑随机因素的空中交通流量预测模型研究[J].中国民航大学学报，2008，26(4):59-61.

ZHAO Yuhuan，GUO Shuang.Research on the forecast method for air traffic flow considering random factors[J].Journal of China Civil Aviation University，2008，26(4):59-61.

[6]BOUGAS C.Forecasting air passenger traffic flows in canada:an evaluation oftimeseriesmodelsand combinationmethods[D]. [S. l.]:Constantinos Bougas，2013.

[7]MALLAT S G.A theory for multiresolution signal decomposition:the wavelet representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(7):674-693.

[8]MENON P K，SWERIDUK G D，BILIMORIA K D.New approach for modeling，analysis，and control of air traffic flow[J].Journal of Guidance，Control，and Dynamics，2004，27(5):737-744.

[9]ROY S，SRIDHAR B，VERGHESE G C.An aggregate dynamic stochastic model for an air traffic system[C]∥Proceedings of the 5th Eurocontrol/Federal Aviation Agency Air Traffic Management Research and Development Seminar.Budapest:[s.n.]，2003:1-10.

[10]SRIDHAR B，SONI T，SHETH K，et al.Aggregate flow model for air-traffic management[J].Journal of Guidance，Control，and Dynamics，2006，29(4):992-997.

[11]SRIDHAR B，CHEN N Y，NG H K.An aggregate sector flow model for air traffic demand forecasting[C]∥ 9th AIAA Aviation Technology，Integration， and Operations Conference(ATIO).[S.l.]:NASA Ames Research Center，2009:1-12.

[12]张静，徐肖豪，王飞.天气季节性影响的机场到达容量概率分布[J].西南交通大学学报，2011，46(1):154-161.

ZHANG Jing，XU Xiaohao，WANG Fei.Probability distribution for airports'arriving capacity considering seasonal weather effects[J]. Journal of Southwest Jiaotong University，2011，46(1):154-161.

[13]PETRIS G，PETRONE S，CAMPAGNOLI P.Dynamic linear models with R[M]. New York:Springer-Verlag，2009:41-74.

[14]COSHALL J T.Combining volatility and smoothing forecasts of UK demand for international tourism[J].Tourism Management，2009，30(4):495-511.

[15]WEST M，HARRISON P J.Bayesian forecasting and dynamic models[M].2nd ed.New York:Springer-Verlag，1997:20-27.