基于MATLAB和GM（1，1）模型的预测方法应用实例

王慧蕾

（广东外语外贸大学，广州 510006）

基于MATLAB和GM（1，1）模型的预测方法应用实例

王慧蕾

（广东外语外贸大学，广州 510006）

GM（1，1）模型是灰色系统的重要组成部分，被应用于许多领域，结合MATLAB的计算能力，解决灰色预测模型在矩阵计算方面的问题，同时应用GM（1，1）模型对图书馆数据进行预测，结果可靠。

灰色系统；灰色预测；GM（1，1）模型

0 引言

1982年，邓聚龙教授创立了灰色系统理论[1]，灰色系统理论是对于“少数据”“贫信息”的不确定性问题的一种新的研究方法。在灰色系统理论中，“黑色”被用来表示未知信息；“白色”被用来表示已知信息；“灰色”则表示部分已知部分未知的信息。这种含有部分已知信息部分未知信息的研究对象的系统就叫做灰色系统。灰色系统理论在经济学、金融学、社会科学、数学、统计学、国际贸易学等社会科学和自然科学等学科上都有广泛的应用。

灰色预测是对不确定性系统进行建模预测的方法之一，是对系统因素发展趋势的差异程度进行鉴别，作关联度分析，同时对系统的原始数据序列进行生成处理。在系统分析中，系统数据常被看成是随机过程，经常运用概率统计的方法对数据进行处理，但是，需要大的数据量才能有效。当系统数据量少时，处理起来就比较困难。灰色系统研究的就是在少量信息下的建模，不是对数据寻求统计规律，而是将这个系统数据的随机过程看成是在一定范围内与时间有关，用数据生成的方法对原始数据进行处理，将原本没有规律的数据使其具有一定规律性[2]，生成具有较强规律性的生成序列，再按某种方法来求解，从而预测事物未来发展规律。灰色系统认为数据表面是杂乱无章的，但是其内部蕴含着一定的规律，灰色系统建模就是在寻找这个内部规律。一阶单变量模型GM（1，1）灰色预测模型是应用于灰色系统理论运算的主要算法之一。当原始序列的数据呈现出指数变化规律时，灰色模型GM（1，1）的解的逼近程度非常好。GM（1，1）模型被很多学者广泛应用[3～4]。

1 方法介绍

GM（1，1）模型的方法是将原始数据经过累加生成规律明显的一次累加生成数据。然后对一次累加生成数据进行建模的方法。

设原始序列为：

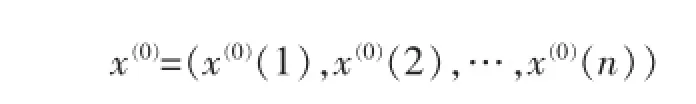
一次累加生成数据为：

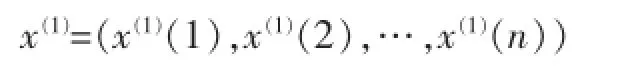
其中:

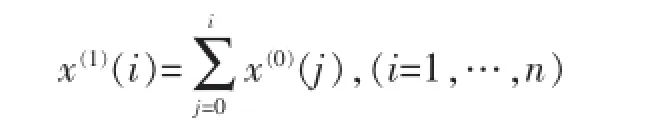
将原始数据累加后，数据的随机性减弱，规律性增强，由于GM（1，1）模型必须建立在离散的光滑的数据的基础上，建模时应对原始数据和一阶累加生成数据进行检验，若符合指数规律，则可以用微分方程来描述。一般检验方法为：

当序列{x（0）（k），k=2，…，n}满足：

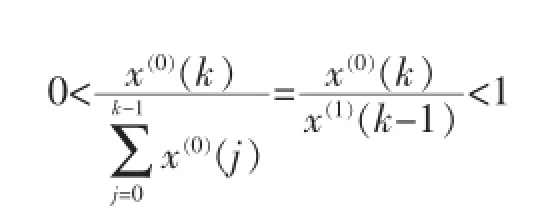
则通过准光滑性检验。

当序列{x（1）（k），k=2，…，n}

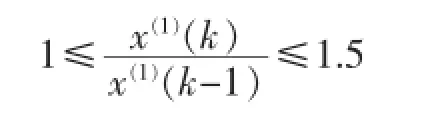
则通过准指数规律检验。

当序列{x（0）（k），k=2，…，n}

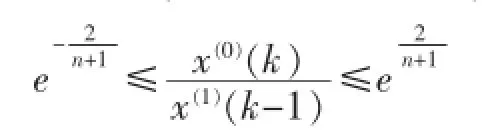
则通过级比检验，此时可对其进行GM（1，1）建模[2]。

GM（1，1）模型是指一阶单变量的微分方程预测模型，一阶微分。其具体形式是：

其中a，b是待识别的灰色参数。a称为发展参数，b称为内生控制灰数。将该式离散化：

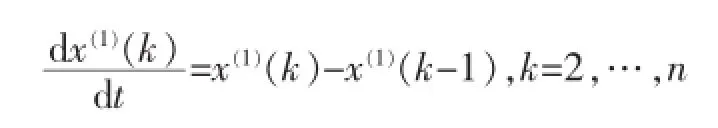
对x（1）作紧邻均值生成

z（1）（k）=0.5x（1）（k）+0.5x（1）（k-1）

用最小二乘法估计a，b

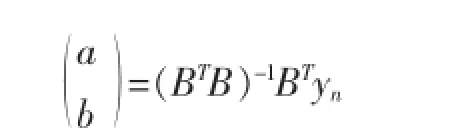
其中：

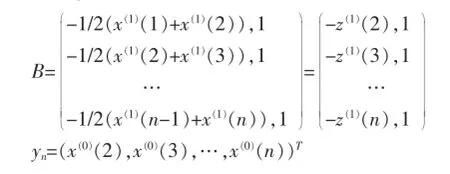
由此可得GM（1，1）模型的时间响应公式为：

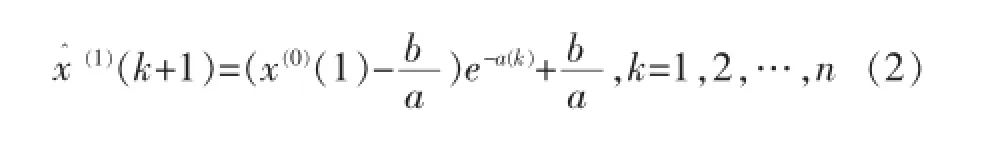
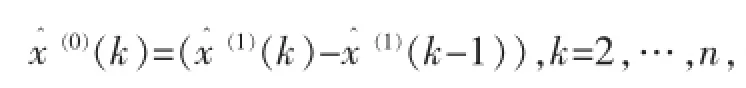
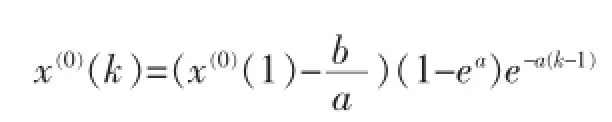
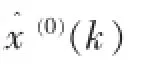
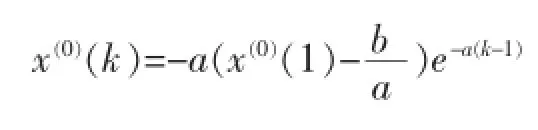
2 模型精度检验

常用的检验有“残差检验”、“后验差检验”、“灰关联检验”、“级比偏差检验”等方法。

（1）残差检验。

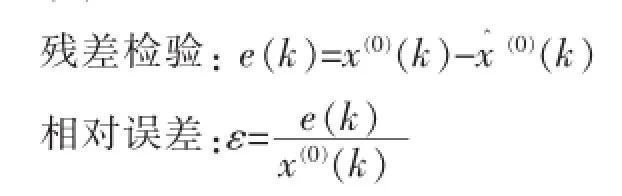
（2）关联度检验

关联度Re是在（0，1）中取定的实数，Re=1时，累加生成值序列与预测值序列完全一致，精度最高；Re=0时，精度最差。一般Re≥0.6时就可满足精度要求。

3 GM（1，1）实例分析

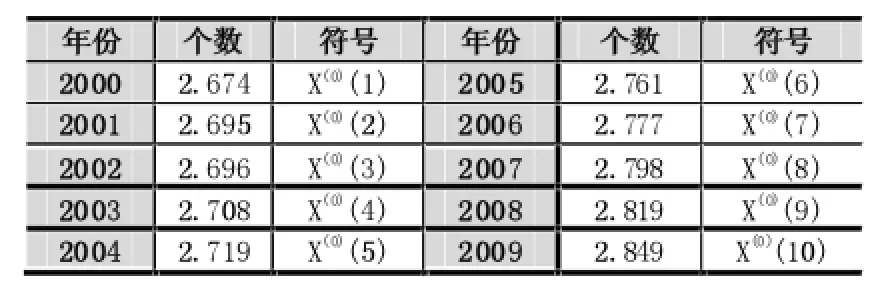
表1 2000～2009年地方公共图书馆个数（单位：千个）

（1）构造原始数据时间序列

x（0）（k）=（2.674，2.695，2.708，2.719，2.761，2.777，2.798，2.819，2.849）

（2）构造累加生成序列

x（1）（k）=（2.674，5.369，8.065，10.773，13.492，16.253，19.03，21.828，24.647，27.496）

（3）数据序列进行建模可行性分析

准光滑性检验：

准指数规律检验：

级比检验：

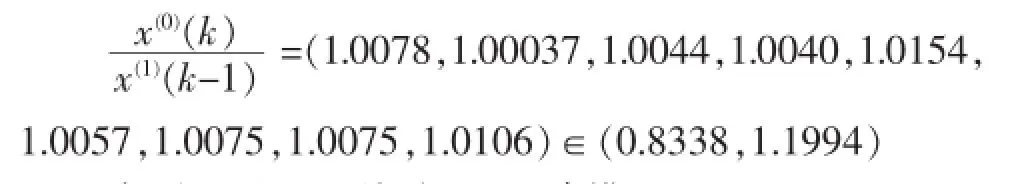
序列通过以上检验，可以建模。

（4）建立GM（1，1）模型

（5）得出预测模型

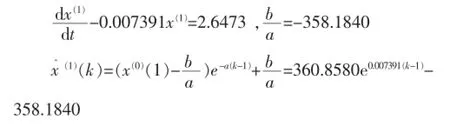
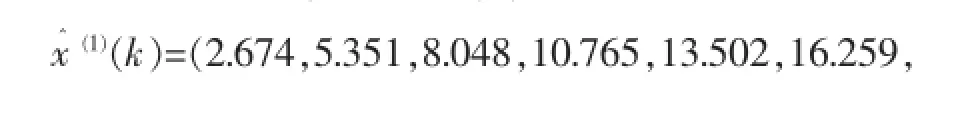
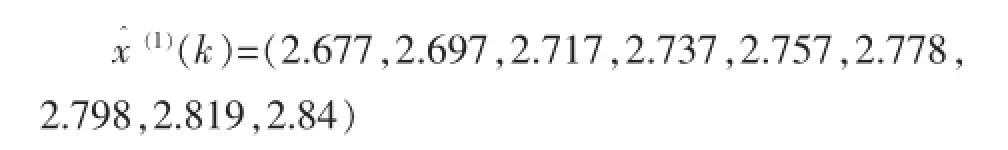
计算预测值的MATLAB语句：

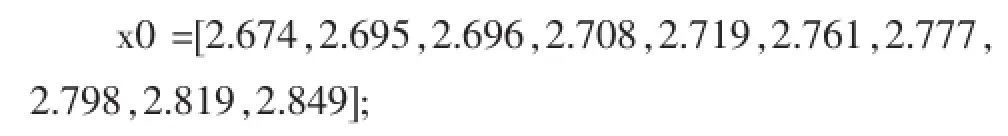
（6）对模型进行精度检验

残差检验后的结果残差值与相对误差如表2所示。

（7）利用经过检验的GM（1，1）模型进行预测

根据这一公式计算出2000～2009年度预测值，拟和结果验证如表2所示。

表2可以看出，灰色预测模型的结果可以接受，平均误差为0.244%，最大年度误差为0.018（绝对值），模型精确度高。

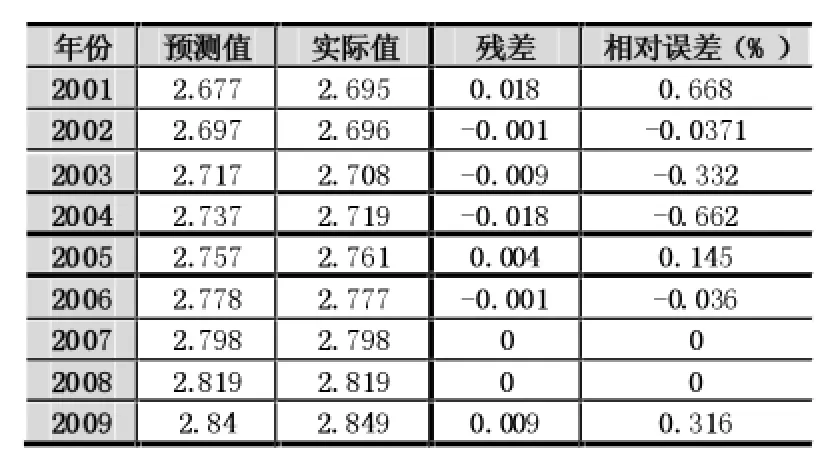
表2 2001～2009年GM（1，1）预测结果（单位：千个）

4 结语

本文通过对灰色系统理论的应用，对全国地方公共图书馆个数进行了预测，建立GM（1，1）模型，并进一步计算了残差，由数据可见，拟合度较好。通过实证分析得到，地方公共图书馆数量逐年增长，并符合一定的规律性。接下来可以通过改进紧邻生成值中的权值0.5，进一步优化模型，可得到更优的预测值，同时做关联度分析可以更好地检验预测精度[5]。

[1] 邓聚龙.灰色预测与决策[M].华中理工大学出版社，1988

[2] 刘思峰，谢乃明等.灰色系统理论及其应用[M].第5版.北京：科学出版社，2010:1～4

[3] 宋秀英.基于MATLAB的灰色预测GM（1，1）模型在经济分析中的应用[J].数学学习与研究，2011（11）：93～95

[4] 唐丽芳，贾冬青，孟庆鹏.用MATLAB实现预测GM（1，1）模型[J].沧州师范专科学校学报，2008（6）：35～37

[5] 魏永棋.用关联度检验灰色系统预测精度[J].江西水利科技，1992，18（4）:322～327

Application Examples of Prediction Method Based on MATLAB and GM（1，1）Model

WANG Hui-1ei
（Guangdong University of Foreign Studies，Guangzhou 510006）

GM(1,1)is an important part of grey theory and has been app1ied to many fie1ds.Combined with the computing matrix with MATLAB, based on the actua1 va1ue,ca1cu1ates 1ibrary data by using GM(1,1)mode1 method.Resu1ts show that the proposed method has higher precision to meet the actua1 demands.

Grey Theory;Grey Prediction;GM（1，1）Mode1

1007-1423（2015）05-0044-04

10.3969/j.issn.1007-1423.2015.05.009

王慧蕾（1978-），女，吉林通化人，硕士，讲师，研究方向为随机过程

2014-12-02

2015-01-20