基于失效分类的应急救援装备预防维修优化

□周 瑜 寇 纲 尔古打机

[1.内蒙古大学 呼和浩特 010021；2.西南财经大学 成都 611130；3.西南民族大学 成都 610041]

一、研究背景

应急救援装备是开展应急救援工作必不可少的条件[1～2]。然而，应急救援装备的使用环境异常复杂，应用条件极其恶劣。因此，应急救援装备的安全性、可靠性和有用性不仅关系着灾区被困人员和救援人员的生命安全，同时还制约着应急救援工作的快速性和有效性[3～6]。其中，运行状态优良的交通工具（汽车和飞机等）就是实施快速救援的可靠保证之一。为了提高交通工具的运行可靠性，本文给出了一种基于失效分类的预防维修优化方法。

对于诸如交通工具这样的复杂系统，基于年龄的成组替换政策[7]和基于失效计数的成组替换政策[8]作为典型政策开发了诸多优化模型。在基于年龄的成组替换政策中，需要根据零部件或子系统寿命由低到高将系统中的零部件或子系统划分为若干组。政策首先确定寿命最小组的预防替换周期，而其他组的预防替换周期为这个值的多重整数倍。顾名思义，基于失效计数的成组替换政策的依据为子系统或零部件的最小修理次数，即最小修理一定次数后进行矫正替换。Nakagawa和Pitchken等则建议综合考虑寿命和最小修理数，管理者需要同时关注系统寿命和最小修理次数，当二者中任意一个指标达到预定值时对系统进行预防替换[9～10]。Muthukumaran等则将车队中车辆的失效函数假定为基于里程的映射关系[11]。孙进康将工程机械系统的一级预防维修周期视为基准[12]。王灵芝等给出了以可靠性为中心的多部件系统预防性维修费用的优化模型[13]。但是，为了方便执行，过于寻求预防替换周期的倍数关系，缺乏对实时状态信息的考虑。

因此，本文基于救援装备的状态信息给出了失效分类方法，并在此基础上给出了一种基于多类别失效计数的预防维修模型。为了验证方法的有效性，以收集的实际数据为例进行了分析。

二、建议预防维修优化方法

（一）失效分类

假设一个由P台同型号车辆所组成的运输车队。车队管理系统记录着车队的失效信息，如失效发生的时间、维修费用和停机时间等。车队的累积失效次数随着运行年龄和行驶里程的增加而单调递增，建模累积失效次数有助于运行、维修调度和决策。文献[14]在未区分失效的严重程度的情况下优化得到运输车辆的预防维修前的最优修理次数为95次，即在发生第96次失效进行预防维修。但在实际情况中，每次失效的严重程度不尽相同，仅以失效次数来优化决策运输车辆的预防维修时间缺乏合理性。因此，本文假定维修费用和停机时间与失效严重程度成正比，初步尝试依据维修费用和停机时间将失效分类。

令失效时间为ti，失效后发生的维修费用和停机时间分别为ci和di。给定c*和d*，以（c*,d*）为界，将失效分为I、II和III类。三类失效的界定范围被直观地显示在图1中。对于c*和d*，本文建议应用分段线性模型对实际观察｛ci｝和｛di｝逼近确定。分段线性模型为：

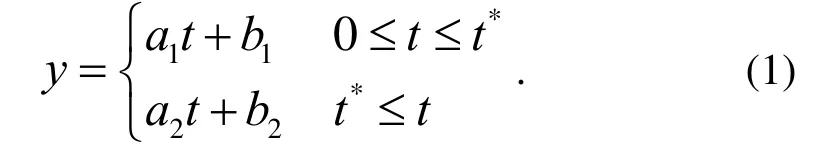
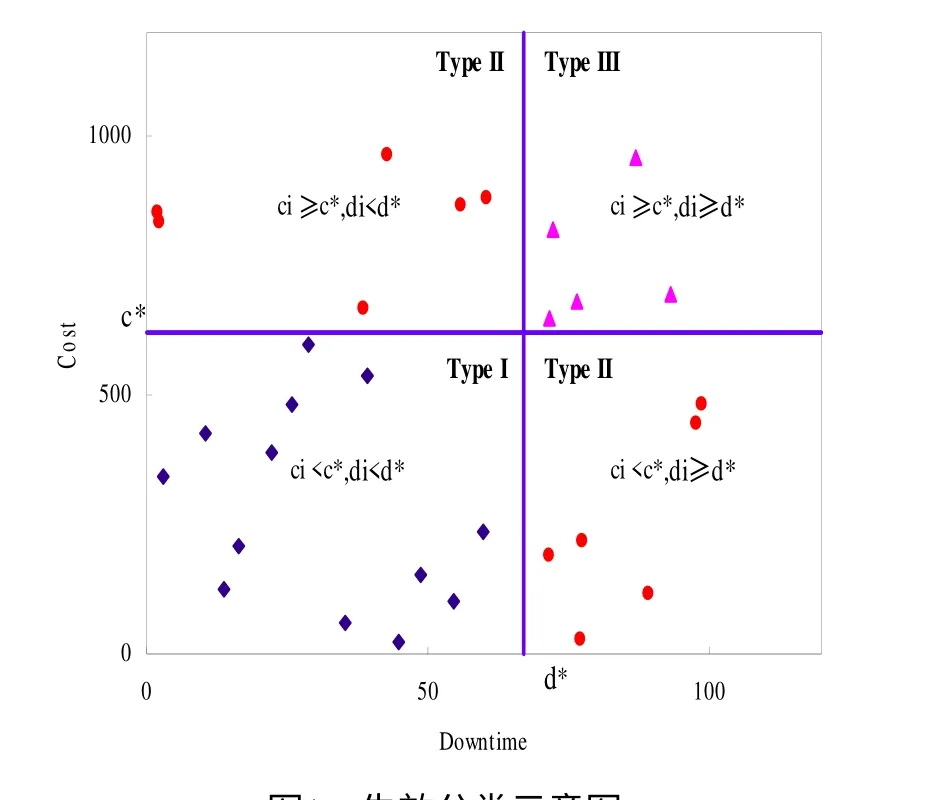
图1 失效分类示意图

对于模型参数，可应用最小二乘法求解。此时，t*和y*就为：

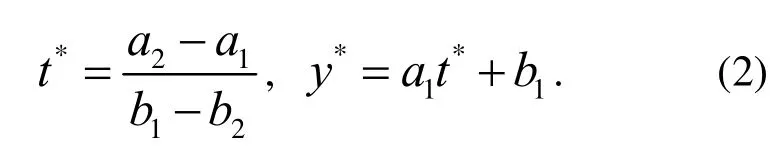
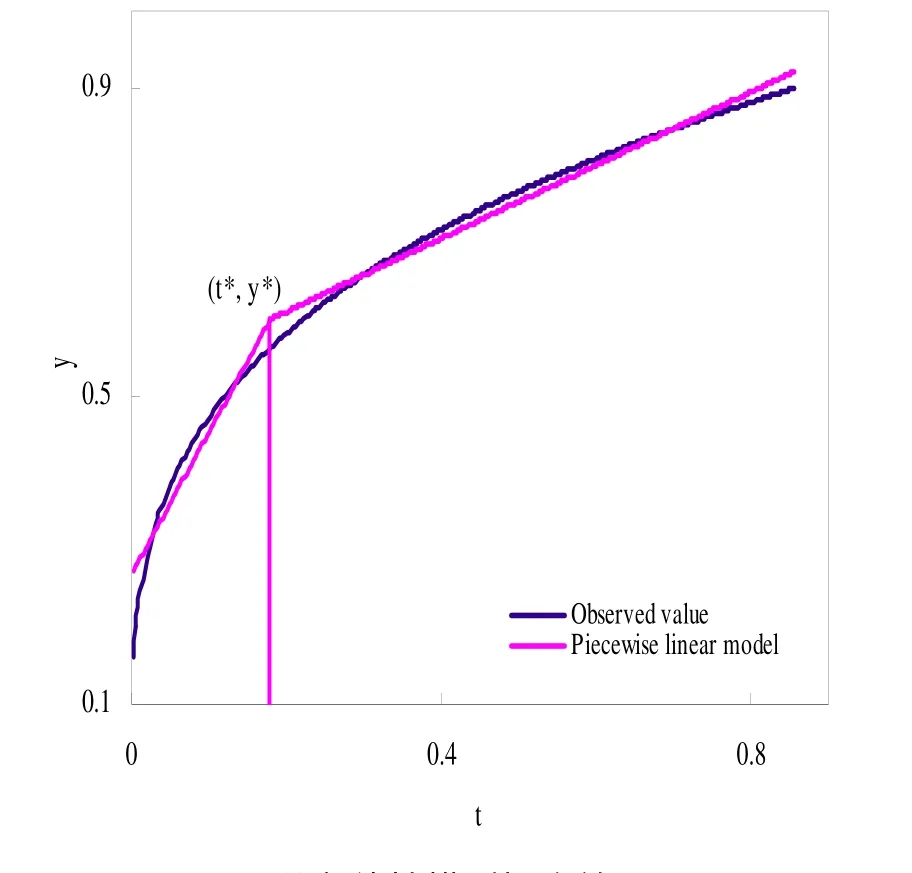
图2 分段线性模型拟合效果图

为了验证该方法的合理性，本文给出了示例，如图2所示。由图可见，拟合的分段线性模型与实际观察非常接近。因此，由此法获得*

y具有一定的合理性。

（二）失效次数建模

失效分类完成后，令N（i）和M（i）分别表示第i次III类失效发生前I类和II类失效的累积失效次数，即：

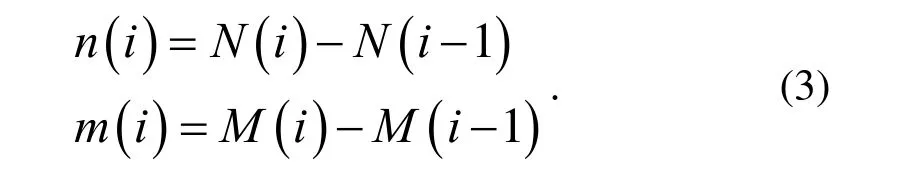
通过进一步整理数据，得到如图3所示的失效历程。其中，i（i=1,2,...,N）标识III类失效，III类失效发生的周次记为Ti，临近的两个III类失效之间发生的I类和II类失效次数分别记为ni和mi。本文应用幂律模型建模III类累积失效次数，以及I、II类失效累积次数与III类失效次数之间的关系。幂律模型为：

其中，E [.]为数学期望，α和β分别为模型参数。

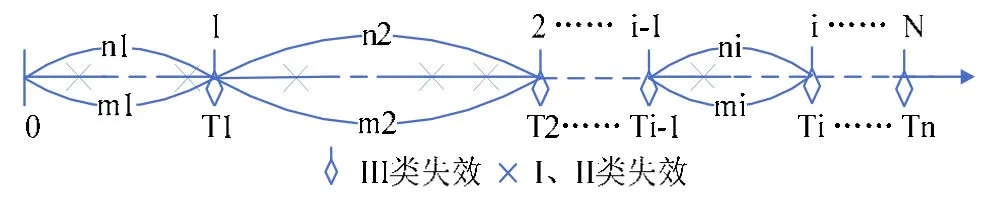
图3 带有失效分类的失效历程

（三）预防维修优化

在失效计数政策基础上，本文考虑在发生第k次III类失效时进行预防维修，假定失效类别III和III的修理费用分别为c1f、c2f和c3f，预防维修费用为cp，则费用率为：

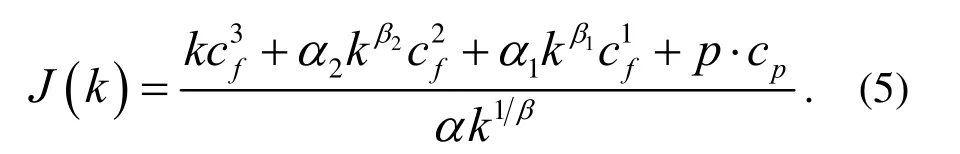
这里，可以通过最小化费用率的方法确定最优k值。

三、数值例子

（一）数据背景

由22辆同型号车组成的某车队于2005年8月24日开始在同一条线路上运行。为了便于管理，该公司于2006年9月1日投入使用了运行管理系统，该系统记录着巴士的运行和失效信息，如油耗、维修费用和停机时间等。本文收集了该车队在2006年9月1日到2009年12月31日的失效数据。由于数据较多，我们仅给出部分数据进行示例，如以表1所示。

表1 车队失效数据

（二）分析过程与结果

步骤1：应用分段线性模型逼近维修费用和停机时间，求得c*=424.20，d*=87.90。根据图1，将3089次失效划分为三类，其中III类失效144次，平均维修费用为1190.00元；II类失效703次，平均维修费用为547.90元；I类失效2242次，平均维修费用57.00元。整理后的数据如表2所示。

表2 失效分类后得到的数据

步骤2：应用幂律模型建模III类累积失效次数，以及III类失效与I、II类失效累积失效次数之间的关系。建模III类累积失效次数得到的模型参数为α=0.0235,β=1.6953。得到的III类失效次数与I、II类失效累积失效次数之间的关系为：

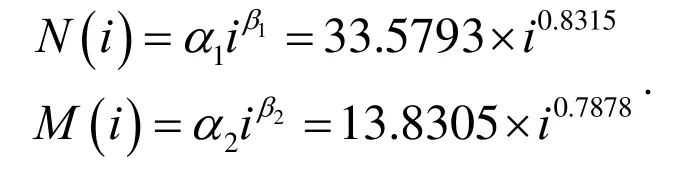
这里，β＞1，1β和β2均小于1，通过分析可以得出：随着使用年龄和运行里程的增加，III类失效发生频率越来越快，且其增长速率快于I、II类失效，车队总体呈现劣化趋势，需要在恰当的时候通过预防维修来改善其劣化趋势。

步骤3：取c1f=100，c2f=550，c3f=1200和cp=10000。经计算，k=109，意味着在车队发生第109次（单台车的第5次）III类失效时应该进行预防维修。如以2006年9月1日为失效计数起点，第109次III类失效发生在之后的第142周（2009年5月）。换句讲，该车队应该在2009年5月份进行预防维修。

应用优化结果于本案例，车队中的18辆车均应在观察截止日前进行预防维修，表3给出了22辆巴士应该进行预防维修的时间。对于4、5和6号巴士，均已经发生过4次III类失效，意味着应该在下次III类失效发生时进行预防维修。

表3 优化结果

四、结论

本文考虑失效的严重程度，并以失效后的维修费用和停机时间为据将失效进行了分类。分类完成后，进行了预防维修决策分析，确定了预防维修前最优的III类失效次数，给出了车队中22辆车应进行预防维修的时间。本研究的主要发现有：

1．维修费用和停机时间可以作为衡量失效严重程度的指标，按维修费用和停机时间将失效进行分类有着一定的合理性。

2．根据失效分类的预防维修决策优化有助于运行、维修调度安排；由较为严重的失效作为预防维修决策优化的主要指标，在日常应急救援装备管理中更容易识别预防维修时机。

[1]范维澄.国家突发公共事件应急管理中科学问题的思考和建议[J].中国科学基金,2007(2):71-76.

[2]田依林.城市公共安全应急管理信息系统建设模型[J].武汉理工大学学报:信息与管理工程版,2007(3):68-71.

[3]彭怡,邬文帅,寇纲,等.突发事件多目标动态应急决策研究综述[J].电子科技大学学报:社科版,2011(2):37-41.

[4]靖鲲鹏,宋之杰,王金艳.应急决策专家管理系统的设计与实现[J].电子科技大学学报:社科版,2012(6):43-46.

[5]KOU G,ERGU D,SHI Y.An integrated expert system for fast disaster assessment[J].Computers & Operations Research,2014,42:95-107.

[6]邬文帅,寇纲,石勇.面向突发事件的模糊多目标应急决策方法[J].系统工程理论与实践,2012(6):1298-1304

[7]SHAFIEE M,FINKELSTEIN M.An optimal age-based group maintenance policy for multi-unit degrading Systems with application [J].Reliability Engineering & System Safety,2014.

[8]YOO Y K.Operating characteristics of a failure counting group replacement policy [J].International Journal of Systems Science,2010,42(3):499-506.

[9]NAKAGAWA T.Optimal number of failures before replacement time [J].IEEE Transactions on Reliability,1983,32(1):115-116.

[10]RITCHKEN P,WILSON J.(m,T) group maintenance policies [J].Management Science,1990,36(5):632-639.

[11]MUTHUKUMARAN N,MILLER F,FOERSTER J.A methodology for cost effective maintenance scheduling of transit buses [J].Terotechnica,1981,2(4):289-300.

[12]孙进康.工程机械维护保养周期的确定[J].工程机械,1992(1):40-44.

[13]王灵芝,徐宇工,张家栋.以可靠性为中心的多部件系统预防性维修优化研究[J].计算机集成制造系统,2008(10):2042-2046.

[14]JIANG R,ZHOU Y.Failure-counting based health evaluation of a bus fleet[Z].Prognostics and Health Management Conference.Macau，2010(MU3013):1-4.