Proof of the Monotonicity of Grid Size and Its Application in Grid-Size Selection for Mesoscale Models

WANG Chengxin,GAO Shouting,RAN Lingkun,and LIANG Li

1Laboratory of Cloud-Precipitation Physics and Severe Storms,Institute of Atmospheric Physics, Chinese Academy of Sciences,Beijing 100029

2University of Chinese Academy of Sciences,Beijing 100049

3State Key Laboratory of Severe Weather,Chinese Academy of Meteorological Sciences,Beijing 100049

4Public Weather Service Center,China Meteorological Administration,Beijing 100081

5National Meteorological Center,China Meteorological Administration,Beijing 100081

Proof of the Monotonicity of Grid Size and Its Application in Grid-Size Selection for Mesoscale Models

WANG Chengxin∗1,2,GAO Shouting1,3,RAN Lingkun1,and LIANG Li4,5

1Laboratory of Cloud-Precipitation Physics and Severe Storms,Institute of Atmospheric Physics, Chinese Academy of Sciences,Beijing 100029

2University of Chinese Academy of Sciences,Beijing 100049

3State Key Laboratory of Severe Weather,Chinese Academy of Meteorological Sciences,Beijing 100049

4Public Weather Service Center,China Meteorological Administration,Beijing 100081

5National Meteorological Center,China Meteorological Administration,Beijing 100081

Terrain characteristics can be accurately represented in spectrum space.Terrain spectra can quantitatively ref l ect the effect of topographic dynamic forcing on the atmosphere.In wavelength space,topographic spectral energy decreases with decreasing wavelength,in spite of several departures.This relationship is approximated by an exponential function.A power law relationship between the terrain height spectra and wavelength is f i tted by the least-squares method,and the f i tting slope is associated with grid-size selection for mesoscale models.The monotonicity of grid size is investigated,and it is strictly proved that grid size increases with increasing f i tting exponent,indicating that the universal grid size is determined by the minimum f i tting exponent.An example of landslide-prone areas in western Sichuan is given,and the universal grid spacing of 4.1 km is shown to be a requirement to resolve 90%of terrain height variance for mesoscale models,without resorting to the parameterization of subgrid-scale terrain variance.Comparison among results of different simulations shows that the simulations estimate the observed precipitation well when using a resolution of 4.1 km or f i ner.Although the main f l ow patterns are similar,f i ner grids produce more complex patterns that show divergence zones,convergence zones and vortices. Horizontal grid size signif i cantly affects the vertical structure of the convective boundary layer.Stronger vertical wind components are simulated for f i ner grid resolutions.In particular,noticeable sinking airf l ows over mountains are captured for those model conf i gurations.

terrain spectra,monotonically increasing function,f i tting exponent,the universal grid size,model sensitivity

1.Introduction

The distribution of terrain height variance with waveength is important for determining the required horizontal grid spacing for mesoscale models(Bretherton,1969;Young nd Pielke,1983;Srinivasan and Ramanathan,1994;Ramanathan and Srinivasan,1995;Salvador et al.,1999).Terain height variance plays a key role in the simulation of mesoscale atmospheric f l ows.The ability to simulate local irculation and rainfall accurately relies heavily on resolving he important terrain features over the area of focus.Howver,the gridresolutionis veryoftenselected withoutconsidring its optimum value(Salvador et al.,1999).Thus,analysis of the terrainheight varianceis a necessary(althoughnot suff i cient)step in the processofestablishingthe requiredhorizontal grid size for a mesoscale model application(Pielke, 1984).The spectral analysis of terrain height variance gives an idea about the dominant wavelengths(λ)of terrain variance,which are used to specify the horizontal grid spacing required to resolve topographic perturbations without resorting to the parameterization of subgrid-scale terrain variance in mesoscale models.

Results of previous studies of terrain spectra have varied considerably,depending on the geomorphology of the study region because terrain variances vary between different landscapes(Bretherton,1969;Young and Pielke,1983; Young et al.,1984;Salvador et al.,1999;Denis et al.,2002; Wang and Wang,2004;Perron et al.,2008;Booth et al., 2009).For example,Young and Pielke(1983)found a linear λ-dependence for three different cross sections of Colorado, and an upperboundof 0.1 km formesoscale models based onone-dimensional terrain spectra.Srinivasan and Ramanathan (1994)found terrain height variances proportional toλ2for threecrosssectionsofthePuneregion,anddeterminedaminimum horizontal grid spacing of 4 km to resolve 87%of the terrain variance.Salvador et al.(1999)obtained a mean exponent of 1.77 for four sections of Castellon,and determined a grid size of 2 km for mesoscale models of the region.Since the optimum horizontal grid spacing varies among different regions,the grid size for each region must be individually determined in mesoscale models.Analysis of many terrain cross sections to obtain accurate f i tting exponents and computed grid sizes for each region is highly desirable.The minimum grid size can be selected for mesoscale models of this region because it is f i t for the study of any case,though not the optimum size for many cases.Thus,for every case study in the area of focus,the minimum grid size is a suff i cient (although not necessary)condition to resolve the majority of terrain height variance.

It is computationallytime-consuming to calculate the optimum grid size through trial and error of many different grid sizes.Finding a mathematical relationship between the grid size and the exponent greatly decreases the computational effort.The aim of this paper is to investigate the mathematical relationship between the grid size and the exponent. Estimation of the universal grid size for mesoscale models of the landslide-prone areas in western Sichuan is used as an example.The landslide-prone areas cover Wenchuan County and neighboring areas are situated in the steep hills north of Sichuan’s provincial capital,Chengdu.Earthquakes in Wenchuan result in f i ssures,loosening of the geological structure and the formation of a slippage surface,apt to form a landslide when heavy rain occurs.Studies of rainfall in landslide-prone areas,where topographic-scale forcing has an important effect on mesoscale atmospheric f l ows and therefore on the distribution of precipitation,are essential.Additionally,in choosing the universal grid size for mesoscale models of landslide-prone areas,it is also important to assess model sensitivity to different grid resolutions (Salvador et al.,1999;Kain et al.,2008;Roberts and Lean, 2008;Schwartz et al.,2009).Thus,several simulations using different grid resolutions for the mesoscale numerical model are undertaken to illustrate the inf l uence of grid size.

2.Data and methods

2.1.Topography data

For simulations in landslide-prone areas,a domain of nested grids with a 1-km topographicresolution is often used in mesoscale models.To study f i ne terrain detail,the topographic resolution is increased.This allows the study of atmospheric f l ows,and a more detailed distribution of precipitation for the landslide forecast.The latest SRTM 90 m digital elevation database,originally produced by National Aeronautics and Space Administration(NASA),is used as the basic dataset for spectral analysis.The landslide-prone studyregioninwesternSichuanis shownin Fig.1.Thestudy region covers(30.52°–31.72°N,102.86°–104.16°E),with a near constant zonal distance of 123.6 km and a meridional distance of 133.6 km,corresponding to the zonal and meridional grid points of 1561 and 1441,respectively.The actual topographic resolutions in the zonal and meridional directions are 79.2 m and 92.8 m,respectively.The terrain elevations are calculated along seven adjacent zonal cross sections and seven meridionalcross sections,both with a regular interval of 0.2°.

2.2.Spectral analysis

Spectral analysis has been used for several years for diagnostic purposes(Boer and Shepherd,1983;Trenberth and Solomon,1993).Fourier transformation is used to analyze and separate the spectral signal to provide information on spectral characteristics(Rayner,1972;Hanley,1977;Ricard et al.,1987;Ansoult,1989;Hough,1989;Goff and Tucholke,1997).Topographic data are discrete,so a Discrete Fourier Transform(DFT)is used to retrieve the spectral distributions in frequency space.For the landslide-prone areas, the one-dimensional terrain height variance spectra are computed separately for each of the terrain height cross sections. For each cross section,a linear trend is f i rst calculated by a least-squares f i t and then subtracted from the terrain height series.The DFT routine is applied over the resulting height values,and the resulting spectra depict the distribution of terrain height variances in either wavenumber(k)or wavelength (λ=1/k).A power law relationship between the terrain height spectra(S)andλwith the form S=aλbis f i tted using the least-squares method.The coeff i cient a represents the intensity of topographic forcing,and the exponent b ref l ects the terrain smoothness and is used to discuss the selection of horizontal grid spacing for mesoscale models.

A two-dimensionalspectrumanalysis canbe achievedusing a two-dimensional fast Fourier transform(2DFFT).If a percentage of the maximum spectral energy is required for atopographic effect,an average wavelength meeting that condition can be found by averaging the spectral energy along the angles def i ned by the horizontal wavenumber(kx)and the vertical wavenumber(ky).The angle is the arc-tangent of the ratio of kxandand the one-dimensional spatial wavenum-However,this method is computationally intensive,and is thus an inconvenient and uneconomical method for obtaining optimum model grid spacing. YoungandPielke(1983)and Younget al.(1984)verif i edthat spatial spectral analysis of a two-dimensional topographic prof i le can be replaced by a one-dimensional prof i le in the following manner.Since then,the one-dimensional algorithmalongseveraladjacentcross sectionsof terrainhas been widely used for the convenience of calculation(Young et al., 1984;Srinivasan and Ramanathan,1994;Ramanathan and Srinivasan,1995;Hsu et al.,2006).

2.3.Model and experiment design

The Advanced Regional Prediction System(ARPS,version 5.3.0),initially developed at the Center for Analysis and Prediction of Storms(CAPS)at the University of Oklahoma, is used to simulate a rainstorm process that occurred in the landslide-proneareas from 9–10July 2013.The latest SRTM 90m digital elevationdatabasereplaces theold terraindata in the ARPS.Nesting capabilities are not considered,to avoid in fl uences on the model results other than those caused by horizontalgrid spacing.In the vertical direction,53 unevenly spaced full sigma levels are established.The initial conditions and boundary data are from the European Centre for Medium-Range Weather Forecasts(ECMWF)global data, which have a horizontal resolution of 0.5°×0.5°.The model physics packages include the Lin Ice microphysics scheme (Zhao and Xue,2009),the Kain–Fritsch cumulus parameterization scheme(Kain and Fritsch,1990),the NASA atmosphericradiationtransferparameterization,andsurface fl uxes calculated from constant drag coef fi cients for surface layer parameterization.The experiment is performed for 24 hours starting at 0000 UTC 9 July 2013.Four different model confi gurations of horizontal grid size(9.2,6.6,4.1,and 1.9 km) are tested.The observed precipitation consists of conventional surface station data from the National Meteorological Center(NMC)of the China Meteorological Administration (CMA).

3.Results and discussion

3.1.The terrain spectra of different cross sections

The zonal distributions of terrain height variance spectra versus wavenumber(km−1)along 30.72°N and 31.32°N are shown in Fig.2.The discrete nature of the terrain data means that the smallest resolvable wavelength(maximum wavenumber)measuredin terrainspectrumspace is twice the grid resolution of terrain.In Fig.2a,the minimum resolvable wavelength is 0.16 km(wavenumber 6.3 km−1),though the spectral energy for wavenumbers larger than 1 km−1(λ＜1 km)is close to zero,as shown in Fig.2b.Terrain height variance spectra reveal the effect of topographic dynamic forcing on the atmosphere,and the greater the spectral energy then the stronger the topographic dynamic forcing(Pielke, 1984).In Fig.2a,the maximum topographic spectral energy is 11.8×106m2km,indicating undulation of terrain and maximum topographic dynamic forcing.The dominant wavelength(DW)corresponding to the maximum spectral energy is 61.8 km,under which the spectral energy declines with decreasingλ,implying that the topographic dynamic forcing weakens with the gentleness of the topographic relief.Nevertheless,a sudden increase of spectral energy exists at a wavelength of 20.6 km for the complex terrain,though it does not affect the overall downward trend.Similarly in Fig.2b,the DW is 41.2 km,corresponding to the maximum spectral energy of 12.3×106m2km,larger than the value for the cross section along 30.72°N.It indicates that the undulation of terrain along 31.32°N is more pronounced than along 30.72°N,implying stronger topographicdynamic forcing along 31.32°N.Whenλ＜DW,the forcingweakens with decreasingλ,though there are sporadic departures from this trend.

The distributions of meridional terrain height variance spectra for the cross sections along 103.86°E and 104.06°E are shown in Fig.3.In Fig.3a,the DW is 66.8 km,corresponding to the maximum spectral energy of 8.5×106m2km;the secondary wavelength is 16.7 km,corresponding to a spectral energy of 2.0×106m2km.The relatively large spectral energies here both show strong topographicdynamic forcing.Forthecrosssectionalong104.06°E,thespectralenergy takes the dominating peak value,less than the value of 8.5×106m2km,whichindicatesthatthetopographicforcing along 104.06°E is weaker than along 103.86°E.Also,from the zonal(Fig.2)and meridional(Fig.3)terrain spectra,the maximum topographic spectral energy in the zonal direction is largerthaninthe meridionaldirection,implyingthattheeffect of topographic dynamic forcing on the atmospheric systemoverterrainis zonallystrongerthanthatin themeridional direction.In addition,the longer wavelength corresponds to a more prominent topographic relief,and therefore the larger spectral energy,and the shorterwavelength,shows a less pronouncedterrainheightvarianceanda smaller spectralenergy. There is a downward topographic spectral energy trend with decreasingλ,in spite of several departures,and this decreasing trend has an approximately exponential form.Thus,a power law relationship between the terrain height spectra(S) and variableλin the form ofS=aλbis fi tted by the leastsquares method.In this equation,the coef fi cientarepresents the intensity of topographic forcing,and the exponentbrefl ects the terrain smoothness:greater values ofbcorrespond to more jagged terrain.

3.2.The relationship between the grid size and the exponent b

For the purpose of mesoscale modeling,terrain height variations can be divided into two ranges:those with wavelengths greater than 2∆x(∆xis the grid size for mesoscale models)resolved by the model,and those with wavelengths less than 2∆x;the subgrid-scale terrain variations not resolvable(Pielke,1981).As the effect of the parameterization is uncertain in mesoscale models,it is necessary to choose a value of∆xsmall enough so that the effect of subgrid-scale terrain variations is negligible.An upper bound of∆xis determined by integrating the area under terrain height spectra andrequiringa specif i ed percentageof theterrainheightvariance to be at wavelengths greater than that minimum(Young and Pielke,1983).As mentioned above,the relationship between the terrain height spectra and variableλhas the form ofS=aλb,and the ratio of subgrid-scale terrain height variance to model resolved terrain height variance(r)is

wherekis wavenumber,2δxis the shortest wavelength in the measured spectra,2∆xis the shortest wavelength that can be resolved by the model,andn∆xis the model domain length. Equation(1)integrates to

SettingL=n∆x/2,we have the expression forr:

The percentage ofris specif i ed in advance and is kept constant for a f i xed region.Generally,resolving 90%of the terrain variance is suff i cient to consider the topographic forcing without a subgrid-scale parameterization.Thus,we obtain an expression for∆xin three variables,L,δxandb:

For the study region,the domain is divided into several adjacent cross sections of terrain both in the zonal and meridional directions.As the latitudes(or the longitudes)corresponding to different cross sections vary little,the domain length (2L)is nearly invariable.The grid resolution of terrain,δx, remains unchanged for selected topographic data.That is, the change of∆xdepends only on the variableb.Settingx=b−1,y=∆x,Eq.(4)can be written in the form:

Taking the derivative with respect tox,an expression fory′is found:

If we can prove thaty′＞0,thenyis monotonic with respect tox.Asy＞0 andx2(rLx+δxx)＞0,the required relation is:

Dividingboth sides of the inequality[Eq.(7)]by(δx)xtransforms the inequality to the form

AsL/δx＞1,t=(L/δx)x＞1.Also,it is easy to prove thatZ′is a monotonically increasing function with respect tot. Thus,Z′(t)＞Z′(1)=0,indicating a monotonically increasing function ofZwith respect tot.So,

The inequality[Eq.(10)]shows thatyincreases with increasingx,andtherefore∆x(b)is amonotonicallyincreasingfunction.This indicates that the minimum grid size is determined by the minimumb.

3.3.The selection of grid size for mesoscale models of the landslide-prone areas

Since∆xis a monotonically increasing function with respect tob,it is easy to determine the universal grid size for mesoscale models of the landslide-prone areas.The terrain height variance spectra(S)are plotted as a function of wavelength(λ)or wavenumber(k)on a logarithmic scale and f i tted to retrieveaandb.Table 1 displays the values ofaandbfor each of the 14 cross sections.Several zonal and meridional distributions of terrain height variance spectra versus wavenumbers(km−1)in log–logspace arerepresentedinFig. 4 and Fig.5.Using theF-criterion with a signi fi cance level of 0.05,exponentbis signi fi cant.From Table 1,the coef fi cientavaries considerably among these cross sections, because of differing geographic coverage.The exponentbvaries from 1.84 to 3.12 and provides a quantitative measure of terrain smoothness,since the terrain height and the con fi guration are dissimilar.

As shown in Table 1,the minimumbis 1.84 amongseven zonal cross sections of terrain.For terrain height variance spectra of the formS=aλ1.84,the ratio of subgrid-scale ter-

For a mesoscale model of the landslide-prone areas with a zonal domain length of 123.6 km andδxof 0.079 km,a zonal grid spacing of 4.1 km or f i ner is required to resolve 90%of terrain variances without a subgrid-scale parameterization.Similarly,inthemeridionaldirection,a minimumbof 2.09is obtainedamongsevencrosssections.Forameridionaldomainlengthof 133.6kmandδxof 0.093km,the gridresolution of 8.1 km is likely to be the maximum allowable value to resolve adequately the terrain effects.The upper bound of grid spacing in the zonal direction is smaller than that in the meridional direction.Thus,for every case study the horizontal grid spacing of 4.1 km is suf fi cient to resolve 90%of terrain height variance.The value of the percentage of resolved terrain height variance,based on the spectra presented in previous fi gures and for several model grid sizes,is given in Table 2.Assuming that inclusion of 90%of the terrain variance is suf fi cient to correctly consider the topographical forcing,the grid size required for the landslide-proneareas is 4.1 km.

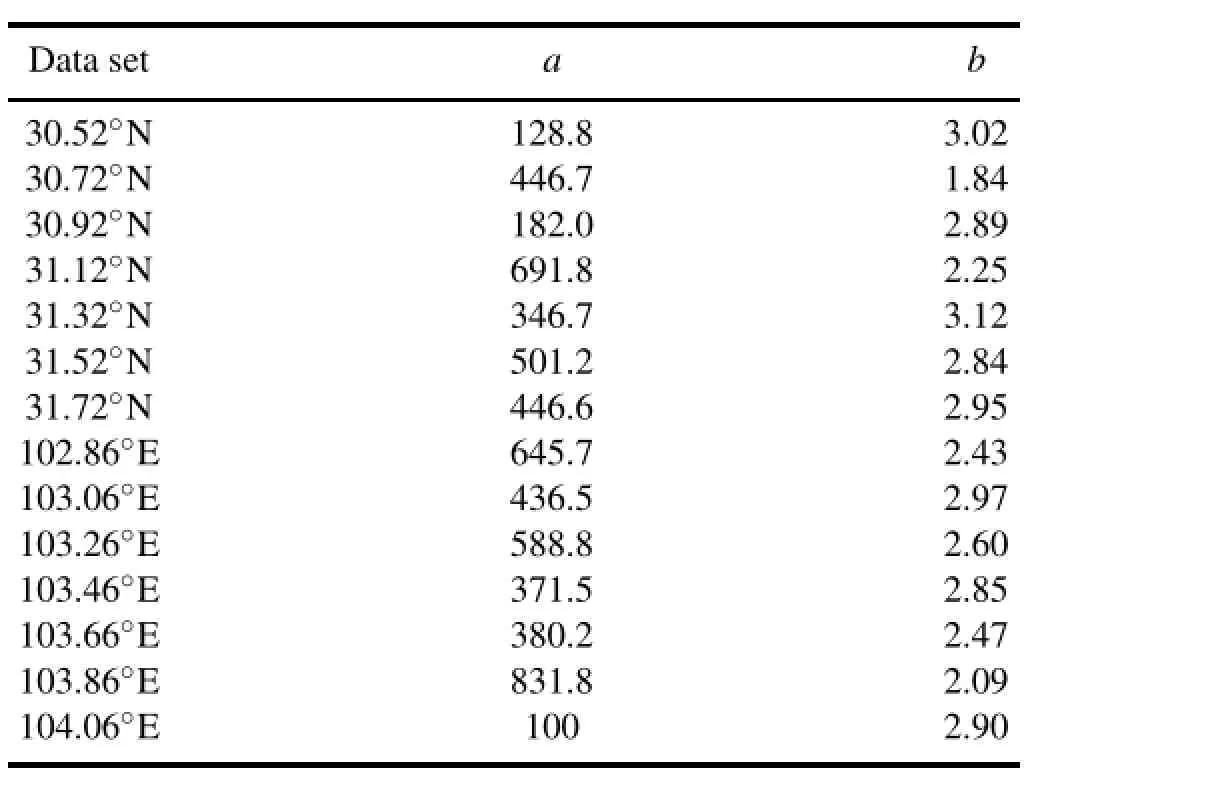
Table 1.Parameters of the least-squares best f i t relationS=aλb, for 14 terrain height variance spectra for the landslide-prone areas.

Although it is assumed that resolving 90%of the terrain variance is suf fi cient to correctly consider the topographical forcing,it does not ensure that all atmospheric phenomena are simulated correctly,but rather that 90%of the terrain infl uenceonatmospheric fl owsis captured.Thespectralenergy of the unresolved topography(10%)is relatively small,indicatingtheinconspicuousundulationofterrainandweaktopographic dynamic forcing.Thus,the effect of the unresolved topography on the atmosphere is ignored.Subgrid-scale terrain variations cannot be completely resolved in the model. It is hard to ascertain whether 90%is suf fi cient for a given application.However,this method allows the calculation of terrain variance(Salvador et al.,1999).

3.4.Model sensitivity to grid resolutions

To show the effect of differing grid sizes on a mesoscale model and better illustrate the results obtainedby the spectral method,several simulations using the ARPS with differentgrid resolutions(Table 2)are performed.Synoptic conditions for the selected days,9–10 July 2013,show a favorable large-scale circulation environment for the occurrence of the rainstorm in western Sichuan(f i gure not shown).During the rainstorm,the atmosphereof West China is controlled by the trough between the Iranian High and the western Pacif i c subtropical high(WPSH);the Sichuan Basin is just at the edge of the WPSH.The steady WPSH keeps the upper trough from moving eastward.Thus,the upper trough stabilizes over West China during the rainstorm,which is conducive to the southeastward movement of the northwestern cold air.The WPSH further causes the southwest low-level jet(SLLJ)to carry warm and moist air into the basin.Subsequently,the southwesterly f l ow transforms itself into an easterly f l ow in the Sichuan Basin,and interacts with the Tibetan Plateau terrain in western Sichuan.In addition,low pressure systemsoriginatingfromtheTibetanPlateauconstantlymove to western Sichuan,leading to rainfall in the west region of Sichuan.

Table 2.The resolved terrain height variance for model resolution and the ratios of unresolved/resolved topography(r)in the mesoscale model.

3.4.1.The comparison of precipitation

The simulated 1-h accumulated precipitation at 1800 UTC and 2100 UTC from the four different model conf i gurations,T-9.2,T-6.6,T-4.1 and T-1.9,which correspond respectively to 80%,85%,90%,and 95%of resolved terrain variance,is selected for the comparison with the observed rainfall.As shown in Fig.6a,the precipitation with a northeast–southwest orientation mainly concentrates in the area from 30.8°N to 31.5°N,with three main centers at(30.8°N,103.1°E),(31.1°N,103.3°E)and(31.2°N, 103.5°E),with values of 22,23 and 25 mm,respectively.In model run T-9.2(Fig.6b),two of the three rainstorm centers are reproduced,although the rain rates are slightly underestimated.Nevertheless,the extent and rain rates around (30.6°N,102.9°E)are highly overestimated.In the T-6.6 run (Fig.6c),the zoneof relativelyheavyprecipitationis approximately 0.2°east of its observed location.A similar overestimation is also simulated around(30.6°N,102.9°E).In T-4.1 (Fig.6d),the simulated result appropriately reproduces the major features of the spatial distributionof precipitation(Fig. 6a).In fact,the simulated zones of maximum precipitation are almost perfectly reproduced,despite a slight disparity inrange compared to the observed precipitation centers.In addition,the maximum precipitation also shows values much closer to the observed maximum.However,the precipitation at some locations is overestimated compared to the observed precipitation(e.g.30.8°N,103.4°E).The model result in T-1.9 is improved only slightly in terms of the spatial distribution of precipitation(Fig.6e)compared to the resolution of T-4.1(Fig.6d).However,the maximum precipitation has heavier values than in T-4.1.

To further demonstrate the simulation’s performance,1-h accumulatedprecipitationat 2100UTCis analyzed.Thesimulated results are shown in Fig.7,and indicate that the simulations of T-4.1(Fig.7d)and T-1.9(Fig.7e)reproduce similar areas of precipitation and maximum precipitation,though with some subtle differences(Fig.7a).In model run T-9.2 (Fig.7b),the shapes of the simulated precipitation areas and zones of maximum precipitation are inconsistent with those of the observed precipitation.The simulation of T-6.6(Fig. 7c)produces more detailed precipitation than that of T-9.2, although slight deviations exist in terms of the location and intensity of the main centers compared to the observed precipitation.

Based ontheanalysis above,the numericalsimulationsof T-4.1andT-1.9appearto performsuff i cientlywell inestimating the observed precipitation.As the grid size decreases,the model captures more features of the observed rainfall distribution in terms of location and intensity.When the grid size is on the order of 4.1 km or less,the model improves only slightly in terms of the spatial distribution of precipitation compared to T-4.1.This is understandable because decreasing grid spacing corresponds to an increase in the percentage of model resolved terrain height variance.This indicates that the topographic dynamic forcing on the atmosphere becomes stronger and therefore yields more detailed precipitation in the landslide-prone areas.When the model resolved terrain height variance reaches a certain proportion(in this paper, 90%),the topographic forcing improves only slightly as the proportion increases,and therefore the model provides an almost identical value of precipitation.

3.4.2.Horizontal pattern of atmospheric f l ow

Figure 8 presents ARPS-simulated wind streamline plots for four different model conf i gurations.Because of the effect of topography,the atmospheric f l ow at 500 hPa is selected. These representations emphasize regions of convergenceand divergence.As shown in Fig.8,although the main f l ow patterns are similar for the four runs,some regions of f l ow divergence and convergence appear at different locations. Simulations T-9.2(Fig.8a)and T-6.6(Fig.8b)fail to simulate the divergence zone around(31.0°N,103.2°E),which is accurately reproduced by the other two runs[T-4.1(Fig.8c) and T-1.9(Fig.8d)].The divergence zone around(30.75°N, 103.35°E)is only simulated by the f i ner resolution grid runs, and this is probably related to the terrain resolution.Furthermore,the divergence zone around(30.75°N,103.05°E) is noticeable in simulations T-9.2,T-4.1,and T-1.9,though T-4.1 and T-1.9 have more complex streamline patterns.Besides this,from the comparison between T-4.1 and T-1.9, some features of the f l ow induced by topographyappear only in the f i ner resolution grid run(Fig.8d),though the majority of the f l ow patterns are almost identical for the two runs.These features include the vortices around(30.9°N,103.1°E)and(30.9°N,103.4°E)and the convergence zone around(31.5°N,103.7°E),also not simulated in the T-9.2 or T-6.6 runs.In general,as grid size decreases,the model producesmorecomplexf l owpatternsthatshowsomedivergence and convergencezones,and vortices.

3.4.3.Vertical pattern of atmospheric f l ow

The simulated vertical motions are quite sensitive to the horizontal grid size used in the model.The vertical structure oftheconvectiveboundarylayer,simulatedbythefourmodel conf i gurations,shows signif i cant differences.Figure 9 shows the combined east–west wind component and vertical wind component plotted on the cross section along 31.3°N at 1800 UTC 9 July 2013.The section spans across the mountains with the most evident terrain undulation.The easterly f l ow followsthemountainsurfacesandgeneratesup-slopeandupvalley wind systems,thus inducing convergenceand updrafts nearthe peaks.These cross sections show that f i ner gridsizes correspond to higher and more intense vertical updrafts.The maximumvertical wind componentsin the convergencezone over 103.35°E are 0.4 m s−1on the coarser grid(9.2 km), 0.8 m s−1using the 6.6 km grid,and 1.2 m s−1on the f i ner grids(4.1 km and 1.9 km).Generally,the inclusion of a f i ner gridincreasestheabilityofmeteorologicalmodelstoproduce larger vertical motion,since small-scale horizontal temperature gradients and velocities are resolved(Poulos and Pielke, 1994).Vertical updrafts trigger cloud development,and correspond to peak precipitation periods:different updraft rates result in different hydrometeors and therefore different precipitation(Fig.6).In addition,although there is a tendency for convection within the boundary layer in all simulations, the T-9.2 and T-6.6 model runs yield different and more simple patterns than the f i ner-scale runs.For example,vertical currents over 103.6°E appear in all tests;however,the vortex return f l ow hardly appears in the coarser runs(9.2 km and 6.6 km),and is only simulated by the T-4.1 and T-1.9 model runs at about 500 hPa.Furthermore,when using grid sizes of 4.1 km and 1.9 km,noticeable sinking airf l ows over mountains are captured approximately over 103.8°E,103.5°E and 103°E.These downward motions are not simulated by the T-9.2 and T-6.6 model runs.

4.Conclusion

The distributions of the terrain height variance spectra in wavenumber(k)spaceorinwavelength(λ)spacecanbeused to determine the spatial scales of a given terrain.Taking the landslide-prone areas in western Sichuan as an example,the maximum topographic spectral energy shows the most evident undulation of terrain and the maximum topographic dynamic forcing.The trend of the topographic spectral energy is downward with decreasingλ,and this decreasing trend is described by a power law relationship between the terrain height spectra(S)and variableλin the form of S=aλb. Fitted by the least-squares method,the spectral slope(−b) in log–log space is associated with grid-size selection for mesoscale models.As the domain length is nearly constant, and the minimum resolvable wavelength in terrain spectrum space remains unchanged for the selected topographic data, the change of∆x depends only on the exponent b.Furthermore,the monotonicity of grid size is investigated,and it is proven that∆x(b)is a monotonically increasing function.This indicates that the universal grid size selected for mesoscale models is determined by the minimum b.Using this mathematical relationship between∆x and b,a universal horizontal grid spacing of 4.1 km is required to resolve 90% of the terrain height variance for mesoscale models,without resortingtotheparameterizationofsubgrid-scaleterrainvariance for the landslide-prone areas.

The effect of horizontal grid size on model results is analyzed by four model conf i gurations.As the grid size decreases,the model captures more features of the observed rainfall distribution.When the grid size is on the order of 4.1 km or less,the model improves only slightly in terms of the spatial distribution of precipitation compared to T-4.1. Generally,f i nergridsproducemorecomplexpatternswithdivergence zones,convergence zones,and vortices.Horizontal grid size signif i cantly affects the vertical structure of the convective boundary layer.In particular,stronger vertical wind components are simulated for f i ner grid resolutions.Also, noticeable sinking airf l ows over mountains are captured for those model conf i gurations.

Acknowledgements.This study was supported by the Key Research Program of the Chinese Academy of Sciences(Grant No. KZZD-EW-05-01)and the special grant(Grant No.41375052) from the National Natural Science Foundation of China.It was also funded by an open project of the State Key Laboratory of Severe Weather(Grant No.2013LASW-A06).The authors thank the anonymous reviewers for their suggestions,which helped to improve the manuscript.Thanks also go to HUANG Yongjie for his helpful comments.

REFERENCES

Ansoult,M.M.,1989:Circular sampling for fourier analysis of digital terrain data.Mathematical Geology,21,401–410,doi: 10.1007/BF00897325.

Boer,G.J.,and T.G.Shepherd,1983:Large-scale twodimensionalturbulenceintheatmosphere.J.Atmos. Sci.,40,164–184,doi:10.1175/1520-0469(1983)040＜0164: LSTDTI＞2.0.CO;2.

Booth,A.M.,J.J.Roering,and J.T.Perron,2009:Automated landslide mapping using spectral analysis and high-resolution topographic data:Puget Sound lowlands,Washington,and Portland Hills,Oregon.Geomorphology,109,132–147,doi: 10.1016/j.geomorph.2009.02.027.

Bretherton,F.P.,1969:Momentum transport by gravity waves. Quart.J.Roy.Meteor.Soc.,95,213–243,doi:10.1002/qj. 49709540402.

Denis,B.,J.Cˆot´e,and R.Laprise,2002:Spectraldecomposition of two-dimensional atmospheric f i elds on limited-area domains using the Discrete Cosine Transform(DCT).Mon.Wea.Rev., 130,1812–1829,doi:10.1175/1520-0493(2002)130＜1812: SDOTDA＞2.0.CO;2.

Goff,J.A.,and B.E.Tucholke,1997:Multiscale spectral analysis of bathymetry on the f l ank of the Mid-Atlantic Ridge:Modif i cation of the seaf l oor by mass wasting and sedimentation. J.Geophys.Res.,102,15 447–15 462,doi:10.1029/97JB 00723.

Hanley,J.T.,1977:Fourier analysis of the Catawba Mountain knolls,Roanoke county,Virginia.Mathematical Geology,9, 159–163,doi:10.1007/BF02312510.

Hough,S.E.,1989:Ontheuseof spectral methods for thedetermination of fractal dimension.Geophys.Res.Lett.,16,673–676, doi:10.1029/GL016i007p00673.

Hsu,H.M.,M.W.Moncrieff,W.W.Tung,and C.H.Liu,2006: Multiscale temporal variability of warm-season precipitation over North America:Statistical analysis of radar measurements.J.Atmos.Sci.,63,2355–2368,doi:10.1175/JAS3752. 1.

Kain,J.S.,and J.M.Fritsch,1990:A one-dimensional entraining/detraining plume model and its application in convective parameterization.J.Atmos.Sci.,47,2784–2802.

Kain,J.S.,and Coauthors,2008:Somepractical considerations regarding horizontal resolution in the f i rst generation of operational convection-allowing NWP.Wea.Forecasting,23,931–952.

Perron,J.T.,J.W.Kirchner,and W.E.Dietrich,2008:Spectral signatures of characteristic spatial scales and nonfractal structure in landscapes.J.Geophys.Res.,113,F04003,doi: 10.1029/2007JF000866.

Pielke,R.A.,1981:Mesoscale numerical modeling.Advances in Geophysics,B.Saltzman,Ed.,Academic Press Inc.,New York,185–344.

Pielke,R.A.,1984:Mesoscale Meteorological Modeling.Academic Press,San Diego,599 pp.

Poulos,G.S.,and R.A.Pielke,1994:A numerical analysis of Los Angeles Basin pollution transport to the Grand Canyon under stably stratif i ed,southwest f l ow conditions.Atmos.Environ., 28,3329–3357.

Ramanathan,N.,and K.Srinivasan,1995:An estimation of optimumgridsizeforKashmir Valleybyspectral method.J.Appl. Meteor.,34(12),2783–2786.

Rayner,J.N.,1972:Theapplication of harmonic andspectral analysis to the study of terrain.Spatial Analysis in Geomorphology,R.J.Chorley,Ed.,Methuen,New York,283–302.

Ricard,Y.,C.Froidevaux,and R.Simpson,1987:Spectral analysis of topography and gravity in the Basin and Range Province.Tectonophysics,133,175–179,183–187,doi:10.1016/0040-1951(87)90262-9.

Roberts,N.M.,and H.W.Lean,2008:Scale-selective verif i cation of rainfall accumulations from high-resolution forecasts of convective events.Mon.Wea.Rev.,136,78–97.

Salvador,R.,J.Calb´o,and M.M.Mill´an,1999:Horizontal grid size selection and its inf l uence on mesoscale model simulations.J.Appl.Meteor.,38,1311–1329,doi:10.1175/1520-0450(1999)038＜1311:HGSSAI＞2.0.CO;2.

Schwartz,C.S.,and Coauthors,2009:Next-day convectionallowing WRF model guidance:A second look at 2-km versus 4-km grid spacing.Mon.Wea.Rev.,137,3351–3372.

Srinivasan,K.,and N.Ramanathan,1994:Terrain variance spectra for Indian Western Ghats.Proceedings-Indian National Science Academy Part A,60A,133–138.

Trenberth,K.E.,and A.Solomon,1993:Implications of global atmospheric spatial spectra for processing and displaying data. J.Climate,6,531–545,doi:10.1175/1520-0442(1993)006＜0531:IOGASS＞2.0.CO;2.

Wang,W.T.,and Y.Wang,2004:A spectral analysis of satellite topographic prof i le:A coincident pattern between latitudinal topographic and westerly perturbation on the lee side of Qinghai-Tibet Plateau.Journal of Nanjing University,40(3), 304–317.(in Chinese)

Young,G.S.,and R.A.Pielke,1983:Application of terrain height variance spectra to mesoscale modeling.J.Atmos.Sci.,40, 2555–2560.

Young,G.S.,R.A.Pielke,and R.C.Kessler,1984:A comparison of the terrain height variance spectra of the Front Range with that of a hypothetical mountain.J.Atmos.Sci.,41(7),1249–1252,doi:10.1175/1520-0469(1984)041＜1249:ACOTTH＞2.0.CO;2.

Zhao,K.,andM.Xue,2009:Assimilationof coastal Doppler radar data withtheARPS 3DVAR and cloud analysis for thepredictionof HurricaneIke(2008).Geophys.Res.Lett.,36,L12803, doi:10.1029/2009GL038658.

:Wang,C.X.,S.T.Gao,L.K.Ran,and L.Liang,2015:Proof of the monotonicity of grid size and its application in grid-size selection for mesoscale models.Adv.Atmos.Sci.,32(7),1005–1015,

10.1007/s00376-014-4091-6.

(Received 28 April 2014;revised 6 November 2014;accepted 15 November 2014)

WANG Chengxin Email:13429670011@163.com

©Institute of Atmospheric Physics/Chinese Academy of Sciences,and Science Press and Springer-Verlag Berlin Heidelberg 2015