Bounds on the Vertex Co−PI Index of Trees and Unicyclic Graphs∗
2015-05-16KANGChengjunTurangulHasanEminjanSabirElkinVumar
KANG Cheng-jun,Turangul Hasan,Eminjan Sabir,Elkin Vumar
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
0 Introduction
LetG=(V,E)be a finite,connected,and simple graph with vertex setVand edge setE.Thedistance d(u,v)between two verticesuandvis the length of a shortest path connecting them inG.Lete=uvbe an edge inG.The number of vertices ofGwhose distance fromuis smaller than the distance fromvis denoted bynu(e).Analogously,nv(e)is the number of vertices ofGwhose distance fromvis smaller than the distance fromu,whilen0(e)is the number of vertices equidistant fromutov.
Khadikar et al de fined a topological index in[1]and named it Padmakar-Ivan index and abbreviated this topological index asPIindex.The vertex version ofPIindex is de fined in[2]as follows:

Recently,Hasani et al.introduce a new topological index similar to the vertex version ofPIindex in[3].This index is called theCo−PIindex ofGand de fined as:
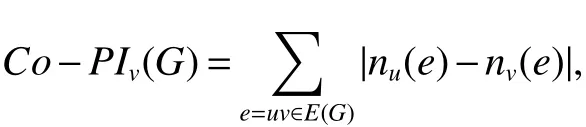
where the summation goes over all edges ofG.
Hasani et al.compute this new index forTUC4C8(R)nanotubes in[3],and in[4]Su et al.present an explicit formula for the vertexCo−PIindex of Cartesian product graphs.In this paper,we study the bounds on the vertexCo−PIindex for trees and unicyclic graphs.
1 Bounds on trees
Lete=uv∈E(T)be an edge of a treeT.The subtreesTuandTvare de fined as the connected components ofT−uvcontaininguandv,respectively.The order of the subtrees is denoted bytu(e)=|V(Tu)|andtv(e)=|V(Tv)|.
Lemma 1LetTbe a tree.Then

ProofAsTis a tree,there is a unique path betweenx∈V(Tu)andy∈V(Tv).Thus,all vertices inTulying closer touthanv.Therefore,tu(e)=nu(e).Similarly,we havetv(e)=nv(e).This implies that
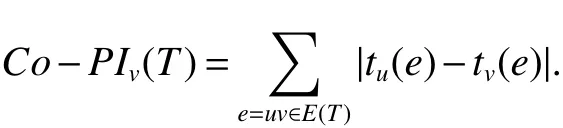
Lemma 2LetG0be a connected graph,w∈V(G0),and letT1andT2be trees withnvertices as shown inFig.1,r≥s≥1.ThenCo−PIv(T1)>Co−PIv(T2).
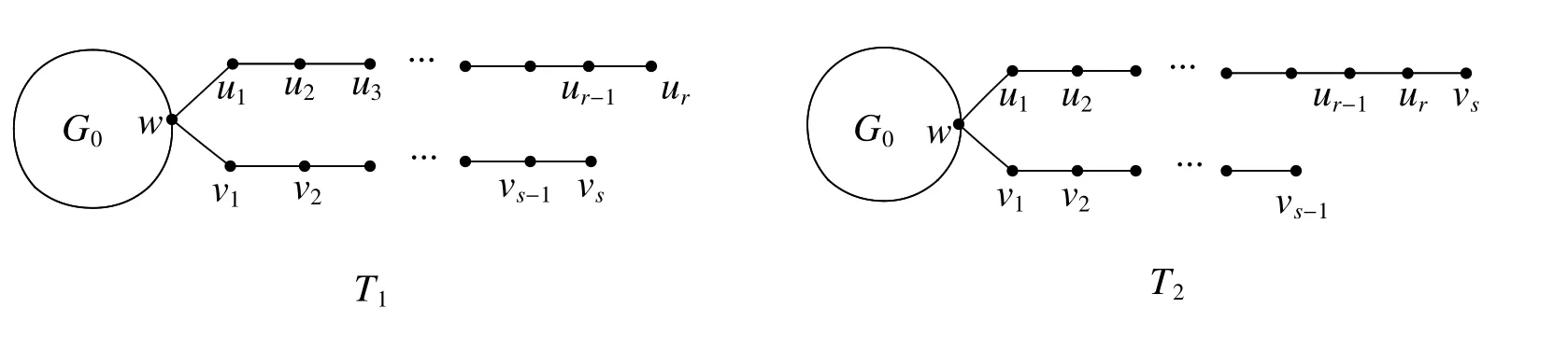
Fig 1 Graph transformation 1:T17→T2
ProofBy Lemma 1,we haveCo−PIv(T1)−Co−PIv(T2)
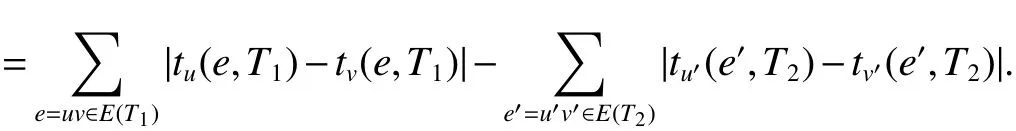
Lete1=wv1∈E(T1)ande2=wu1∈E(T2),we haveCo−PIv(T1)−Co−PIv(T2)=|tw(e1,T1)−tv1(e1,T1)|−|tw(e2,T2)−tu1(e2,T2)|=|n−2s|−|n−2(r+1)|>0.So we haveCo−PIv(T1)>Co−PIv(T2).
Theorem 1LetTbe a tree withnvertices.ThenCo−PIv(T)≤Co−PIv(Sn)=(n−1)(n−2),with equality if and only ifTis a star.

Theorem 2LetTbe a tree withnvertices.ThenCo−PIv(T)≥Co−PIv(Pn),with equality if and only ifT?Pnand
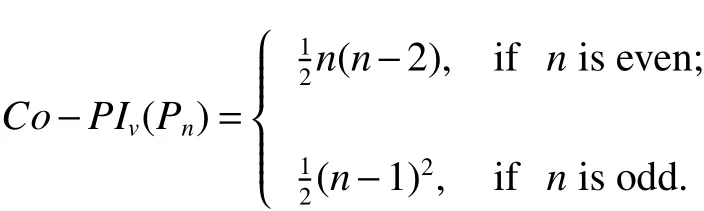
ProofLetTbe a tree withnvertices.IfTis not a path,then,using graph transformation 1 shown in the proof of Lemma 2,we can obtain a series of treesTi(i=1,2,...,s)such thatTsis the pathPn.By Lemma 2,we haveCo−PIv(T)>Co−PIv(T1)>...>Co−PIv(Ti)>Co−PIv(Ti+1)>...>Co−PIv(Ts)=Co−PIv(Pn).So we haveCo−PIv(T)≥Co−PIv(Pn),with equality if and only ifTPn.
2 Unicyclic graphs with minimum and maximum vertex Co−PI index
A connected graph withnvertices andnedges is called a unicyclic graph.LetG=(V,E)be a unicyclic graph of ordernwith its cycleCk=w1w2···wkw1of lengthk.We useto denote a unicyclic graph,whereT1,T2,...,Tkare all trees ofG−E(Ck),andwiis the common vertex ofTiandCk,i=1,2,...,k.In particular,LetCnbe an n-cycle.Letn(Ti)=li+1,i=1,2,...,k,wherel=l1+l2+···+lk=n−k.
Lemma 3LetG0be a connected graph,u∈V(G0),and letG1andG2be graphs as shown inFig.2.Then

Fig 2 Graph transformation 2:G17→G2
ProofBy de finition,we haveCo−PIv(G2)−Co−PIv(G1)

For the edgewe have|nz(e,G1)−nw(e,G1)|=|nz(e,G2)−nw(e,G2)|.For the edgee=uv,we have|nu(e,G2)−nv(e,G2)|−|nu(e,G1)−nv(e,G1)|=|n−2|−|(n−a−1)−(a+1)|≥0.So we haveCo−PIv(G1)≤Co−PIv(G2)as claimed.


Fig 3 Graph Transformation 3:G37→G4,G5,G6,G7.
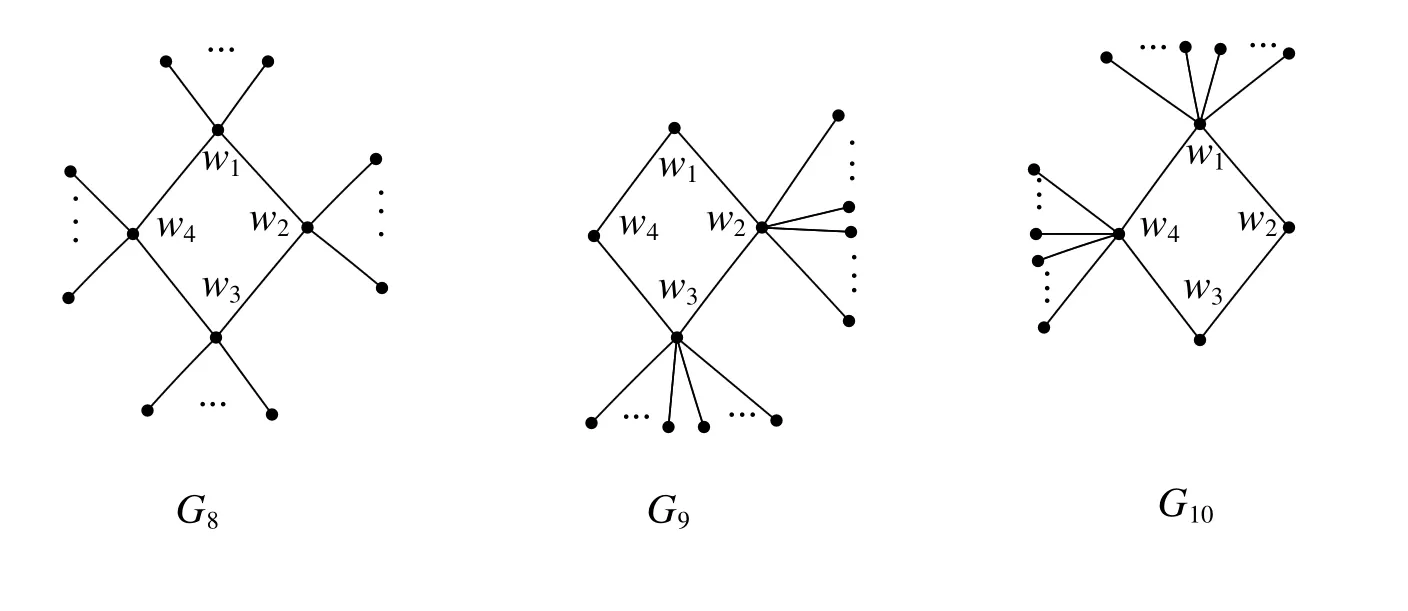
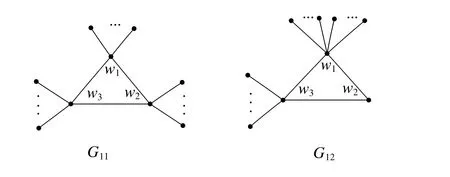
Lemma 4G4,G5,G6andG7be the unicyclic graphs as shown inFig.3 anddegG3(wi)=li+2,1≤i≤k.ThenCo−PIv(G3) ProofIfkis even,by the de finition of vertexCo−PIindex,we haveCo−PIv(G4)−Co−PIv(G3) We consider the graph transformation:For the edgese1=w1w2∈E(G3)ande01=w2u∈E(G4),we haveand for the edgeswe also haveFor the other edges we have So we haveBy the same argument,we also have Ifkis odd,we consider the following four cases. Case 2We consider the graph transformation: Case 3We consider the graph transformation: Case 4We consider the graph transformation: We only prove that in Case 1the other cases can be proved similarly.For the edgeswe haveand for the edgeswe also haveFor the edgesand for the edgesFor the other edgesande=rs∈E(G3),we haveSo we have Lemma 5G9,and letG10be the unicyclic graphs as shown inFig.4,wheredegG8(wi)=li+2(i=1,2,3,4)Then Fig 4 Graph transformation 4:G87→G9,G10. ProofLetei=wiwi+1∈E(G8)and let=wiwi+1∈E(G9),wherei=1,2,3,4 andw5:=w1. Ifnw1(e1,G8)≤nw2(e1,G8).By de finition,we haveCo−PIv(G9)−Co−PIv(G8)= For the edgesFor the other edgesSo we have Ifnw1(e1,G8)>nw2(e1,G8).By the same argument,we also haveCo−PIv(G8) Lemma 6Letbe the unicyclic graphs as shown inFig.5,whereThen. Fig 5 Graph transformation 5:G117→G12. ProofBy de finition,we haveCo−PIv(G12)−Co−PIv(G11)= For the edgese1=w1w2∈E(G11)andwe haveFor the edgese3=w1w3∈E(G11)andFor the edgeswe haveFor the other edges)ande=uv∈E(G11),we have Theorem 3Forn≥3,the cycleCnis the unicyclic graph with the minimum vertexCo−PIindex,which is equal to 0. Theorem 4be a unicyclic graph of ordern≥4 andG?Cn.Then with the equality if and only if ProofFirst,by Lemma 3,we have Case 1kis even.LetBy Lemma 4,we can obtain a series of graphs1,Sle+1,Slf+1))(r,s,e,f=1,2,...,k).We can obtain the graphby applying Lemma 5 repeatedly and we have Case 2kis odd.We can obtain a series of graphsWe can obtain the graphby applying Lemma 6 repeatedly and we hav,the claim follows. Among all unicyclic graphs of ordern≥3,the cycleCnis the one with the minimum vertexCo−PIindex,which is equal to 0.The unicyclic graphhas the maximum vertexCo−PIindex for 4≤n≤ 8 and the unicyclic graphhas the maximum vertexCo−PIindex forn≥ 8.Whenn=8,we haveIn this section,we determine the unicyclic graphs of ordernwith the second,third,fourth minimum and the second maximum vertexCo−PIindex.We useto denote a unicyclic graph,wherePl1+1,Pl2+1,...,Plk+1are paths which have the lengths ofl1,l2,...,lkrespectively,wiis the common vertex ofPli+1andCk,i=1,2,...,k.Particularly,let.Whenn=5,the unicyclic graphsandhave the third minimum vertexCo−PIindex and the unicyclic graphhas the fourth minimum vertexCo−PIindex.Whenn=6,the unicyclic graphshave the third minimum vertexCo−PIindex and the unicyclic graphshave the fourth minimum vertexCo−PIindex,whereS3is joined by a path of length one toC3formT1.Whenn=8,the unicyclic graphhave the fourth minimum vertexCo−PIindex. Proposition 1Consider unicyclic graphs of ordern. (i)Ifnis odd,the unicyclic graphhas the second minimum vertexCo−PIindex forn≥ 5,which is equal to 2n− 3 and the unicyclic graphsandhave the third and the fourth minimum vertexCo−PIindex forn≥7 respectively,which are equal to 2n−2 and 2n+2,respectively. ProofLetGbe a unicyclic graph withnvertices other thanCn. Ifnis odd,we suppose that the unicyclic graphGhas the cycle of lengthn−1 forn≥5.Then the unicyclic graphGis denoted by Suppose that the unicyclic graphGhas the cycle of lengthn−2 forn≥7.We consider the following two cases. CaseA1The two edges which are not in the cycle constitute a pendent path,then the unicyclic graphGis denoted by Case A2The two edges which are not in the cycle constitute two pendent edges,then=(n−2)×2+1×2+2×[(n−4)−(2i−3)]=4n−4−4i.By the graph transformation 1,we haveSo when,the unicyclic graphattains the minimum vertexCo−PIindex in this case which is equal to 2n−2 and Case B1The three edges which are not in the cycle constitute a pendent path,then the unicyclic graphGis denoted by In those three cases,we haveCo−PIv(G)>2n+2 forn≥7. Suppose that the unicyclic graphGhas the cycle of lengthn−k(4≤k≤n−3)forn≥7,we also haveCo−PIv(G)>2n+2.So whennis odd,the desired results followed as respected.By the same argument as above,we can obtain the results whennis even. We use a table to give the unicyclic graphs with the second maximum vertexCo−PIindex for 4≤n≤7 and give the value correspondingly(see table 1). Table 1 The unicyclic graphs with the second maximum vertex Co−PI index for 4≤n≤7 (i)Ifn=8,the unicyclic graphsUhave the second maximum vertexCo−PIindex,which is equal to 38. (ii)Ifn>10,the unicyclic graphhas the second maximum vertexCo−PIindex,which is equal ton2−2n−10. Whenn=9,the unicyclic graphhas the second maximum vertexCo−PIindex,which is equal to 34.Whenn=10,the unicyclic graphshave the second maximum vertexCo−PIindex,which is equal to 70. Fig 6 The unicyclic graphs with the second vertex Co−PI index for n>7. Proof(i)By Theorem 4,we know that the graphshave the maximum vertexCo−PIindex which is equal to 40 forn=8.Asand By the graph transformations:(seeFig.6),the vertexCo−PIindex reduce two.But the vertexCo−PIindex of unicyclic graphsreduce more than two through other transformations.Thus,we conclude that the unicyclic graphshave the second maximum vertexCo−PIindex,which is equal to 38 forn=8. (ii)Forn>10,the unicyclic graphhas the maximum vertexCo−PIindex.By a simple calculation,we haveThat is to say,we haveSo we can obtain that the unicyclic graphhas the second maximum vertexCo−PIindex,which is equal ton2−2n−10.Whenn=9,we haveSo we have the unicyclic graphwith the second maximum vertexCo−PIindex forn=9,which is equal to 54 and the unicyclic graphswith the second maximum vertexCo−PIindex forn=10,which is equal to 70. For 4≤n≤14,it is easy to determine the unicyclic graphs which have the third and fourth maximum vertexCo−PIindex,there are quite a lot of graphs in each case,so we omit to list them.Forn>14,using the same method as that in the proof of Proposition 2,we can obtain the unicyclic graphs of the third and fourth maximum vertexCo−PIindex.Actually,after a simple calculation,it is not difficult to get that there are six unicyclic graphs of the fourth maximum vertexCo−PIindex forn>14,for conciseness we do not list them one by one.Here we list the unicyclic graphs(of ordern>14)with the third maximum vertexCo−PIindex without presenting the proof. Proposition 3Among all unicyclic graphs withnvertices,letbe unicyclic graphs of ordernas shown inFig.7.Then the unicyclic graphhave the third maximum vertexCo−PIindex forn>14. Fig 7 The unicyclic graphs with the third vertex Co−PI index for n>14. References: [1]Khadikar P V.On a Novel Structural Descriptor PI[J].Nat Acad Sci Lett,2000,113-118. [2]Youse fi-Azari H,Ashra fiA R,Khalifeh M H.Computing vertex-PI index of single and multi-walled nanotubes[J].Dig J Nanomat Bios,2008,3:315-318. [3]Hasani F,Khormali O,Iranmanesh A.Computation of the first vertex of co-PI index of TUC4CS(S)nanotubes[J].Optoelectron Adv Mater Rapid Commun,2010,4:544-547. [4]Su G,Xiong L,Xu L.On the Co-PI and Laplacian Co-PI eigenvalues of a graph[J].Discr Appl Math,2013,161:277-283. [5]Dobrynin A,Entrnger R,Gutman I.Wiener index of trees:theory and applications[J].Acta Appl Math,2001,66:211-249. [6]Gutman I,Dobrynin A.The Szeged index-a succrss story[J].Graph Theory Notes NY,1998,34:37-44. [7]Das K C,Gutman I.Estimating the Szeged index[J].Appl Math Lett,2009,22:1680-1684. [8]Klavzar S,Rajapakse A,Gutman I.The Szeged and the Wiener index of graphs[J].Appl Math Lett,1996,9:45-49. [9]Khadikar P V,Kale P P,Deshpande N V,Karmarkar S and Agrawal V K.Novel PI indices of hexagonal chains[J].J Math Chem,2001,29:143-150. [10]Khadikar P V,Karmarkar S,Agrawal V K.A novel PI index and its applications to QSPR/QSAR studies[J].J Chem Inf Comput Sci,2001,41:934-949. [11]Khadikar P V,Karmarkar S,Varma R G.On the estimation of PI index of polyacenes[J].Acta Chim Slov,2002,49:755-771. [12]Hoji M,Luo Z,Vumar E.Wiener and vertex PI indices of Kronecker products of graph[J].Discrete Appl Math,2010,158:1845-1855. [13]Ashra fiA R,Loghman A.PI index of zig-zag polyhex nanotubes[J].MATCH Commun Math Comput Chem,2006,55(2):447-452. [15]Li S,Bian H,Wang G,Yu H.Vertex PI indices of some sums of graphs[J].Ars Combin,2011,98. [15]Li S,Wang G.Vertex PI indices of four sums of graphs[J].Discrete Appi Math,2011,159:1601-1607. [16]You L,Zhu R,You Z.The(weighted)vertex PI index of unicyclic graphs[J].MATCH Commun Math Comput Chem,2012,67(2):383-404. [17]Khalifeh M H,Youse fi-Azari H,Ashra fiA R.Vertex and edge PI indices of Cartesian product graphs[J].Discrete Appl Math,2008,156:1780-1789.


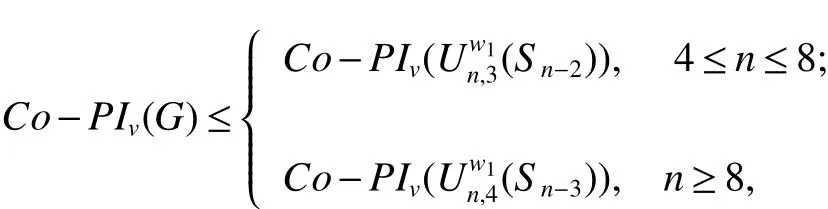

3 Unicyclic graphs with the second,third,fourth minimum and the second maximum vertex Co−PI index

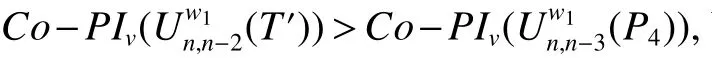
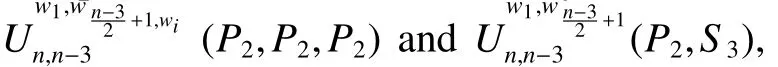
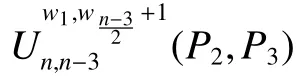



杂志排行
新疆大学学报(自然科学版)(中英文)的其它文章
- WSNs中基于Chebyshev多项式的可认证密钥协商方案∗
- 新疆双峰驼乳清蛋白组分对人宫颈癌HeLa细胞增殖的抑制作用∗
- 新疆加曼特金矿与斑岩型金矿的对比研究∗
- 具有非倍测度的参数型Marcinkiewicz积分交换子在Hardy空间的估计∗
- Periodic Solution of a Two-species Competitive Model with State-Dependent Impulsive Replenish the Endangered Species∗
- Permanence and Extinction for Nonautonomous SIRS Epidemic Model with Density Dependence∗
