Qualitative Analysis of a Antibiotic-resistant Bacteria Model with Different Respond Function∗
2015-05-16GAOYukunMehbubaRehim
GAO Yu-kun,Mehbuba Rehim
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
0 Introduction
Antibiotic resistance is a growing public health concern worldwide.When a person is infected with an antibioticresistant bacterium,not only is treatment of that patient more difficult,but the antibiotic-resistant bacterium may spread to other people.When antibiotics don’t work,the result can be:longer illnesses,more complicated illnesses,more doctor visits,the use of stronger and more expensive drugs,more deaths caused by bacterial infections[1].
Therefore,antibiotic resistance is a serious and growing phenomenon in contemporary medicine and has emerged as one of the pre-eminent public health concerns of the 21st century,in particular as it pertains to pathogenic organisms(the term is especially relevant to organisms that cause disease in humans).There have been many researches in identifying and understanding the factors and biological phenomena responsible for the emergence and spread of drug resistance[2-6].
In order to provide useful insights into the understanding of underlying phenomena and of helpful guidance to related public health decisions,one needs to understand the dynamics of the spreading antibiotic resistance.Some health scientists have tried to obtain some insight in the Antibiotic resistance and the methods of eliminating this phenomena using mathematical modeling.Here,we mention for instance[7-12].Many mathematical models have been devoted to address this issue since then.Recently,progress in mathematical modeling of antibiotic resistance has been accelerated by combining modeling with experimental testing.Based on the new findings in a recent experimental study[11]that antibiotic resistant mutants of bacteria produce indoles to protect the wild strain bacteria,Wendi Wang et al.[13]formulated a mathematical model to describe the evolution of the wild strain,resistant strain and indoles with limited nutrient.The authors in[13]established conditions for co-persistence of both strains,Further analyzed and simulated also revealed some new phenomena not reported in Lee et al.[11],that is,periodic oscillations of the populations may occur within certain range of the parameters,and there exists bistability in the sense that a stable positive periodic solution coexists with a stable positive equilibrium.The nutrient uptake(consumption)rate in the model[13]is taken to be of the Monod(or Michaelis–Menten)form:mxS/(a+S).In this paper,based on the model(1)in[13],for wild strain of bacteria,we want to introduce Monod-Haldene type respond function,the model reads:

whereS,B1andB2denote the concentration of nutrient,wild strain of bacteria,and the antibiotic resistant mutants,respectively.Aistherecruitmentrateofnutrient,disthewashoutrateofnutrientandbacteria,miistheMichaelis-Menten constant,γiis the yield constant representing the conversion efficiency of nutrient to the biomass of the organism,µiaccounts for the maximal growth rate,ε1is the death rate of wild bacteria due to antibiotic in fl uences and ε2is the death rate of its mutants under the antibiotic stress.η/hindicates the maximum absorb rate at which the wild strain bacteria absorbing the indoles.
All the parameters in the model(1)are non-negative in order to have a biological signi ficance.We also assumeµ2<µ1to account for the cost of resistant strain,and assume ε2<ε1to re fl ect the bene fit of antibiotic resistance.
1 Mathematical analysis of the model
Here,we first consider the existence and boundedness of solutions of system(1).And then the stability of the equilibrium points of system(1)are analyzed.This analysis allows us to better understand the role of the altruistic behavior of the resistant bacteria observed in Lee et al[13].In order to do this,we shall consider the following threshold parameters values:

1.1 Positivity and boundedness of solutions
Theorem 1The solution(S(t),B1(t),B2(t),I(t))of system(1)with initial conditionS(0)≥0,B1(0)≥0,B2(0)≥0,I(0)≥0 exist and positive on(0,+∞).Further,
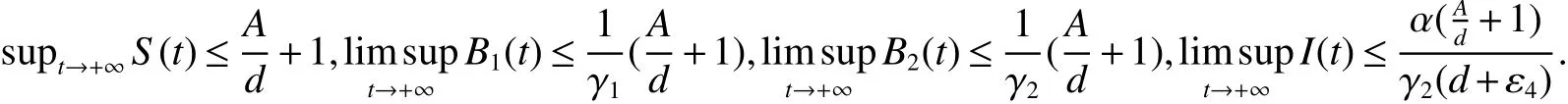
1.2 Existence and stability of the boundary equilibrium
In this section,the equilibrium points of the model are calculated.Obtaining the equilibria is usually the first step in order to know the behavior of a dynamical system.Speci fically,it is shown that the model has an bacterium-free equilibriumE0(S0,0,0,0),thenSinceFrom this we obtain thatR1>1.Therefore,the following results is easy to veri fied
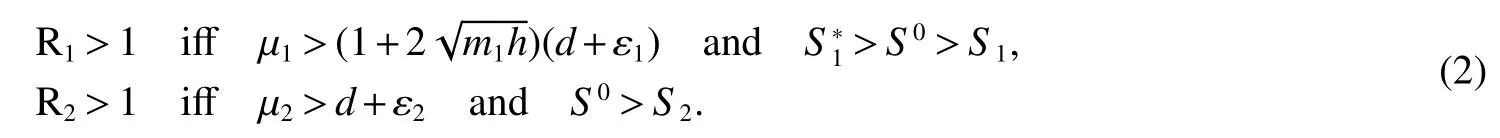
IfB2(t)=0,thenI(t)=0 since indolesI(t)produced by resistant bacteriaB2(t).Thus,if>1,i=1,2,there are two boundary equilibriaE1=(S1,B10,0,0)andE2=(S2,0,B20,I2)in Ω.Where

Here,we consider the local stability ofE1andE2,which gives the thresholds for small invasions of wild strain and resistant strain respectively.
Theorem 2The following statement hold:
(a)Bacterium-free equilibriumE0is asymptotically stable if<1 and is unstable if>1 or>1 or borth of>1,i=1,2.
(b)Assume>1.ThenE1is asymptotically stable if<1,and is unstable if>1.
(c)Assume>1.ThenE2is asymptotically stable if<1,and is unstable if>1.
ProofAt the Bacterium-free equilibriumE0(S0,0,0,0),the Jacobian matrix is
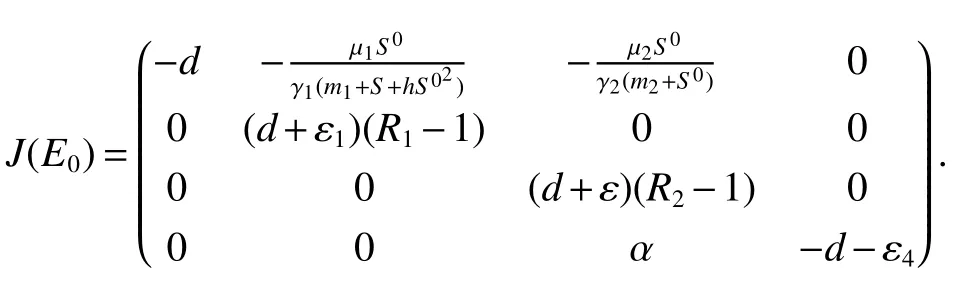
The roots of the characteristic equation of det
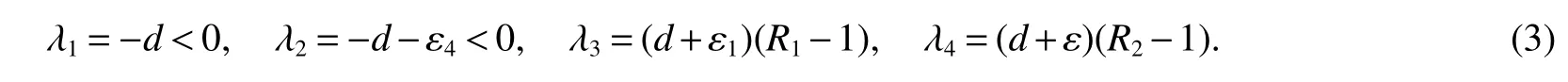
Thus,(a)follows from(3).
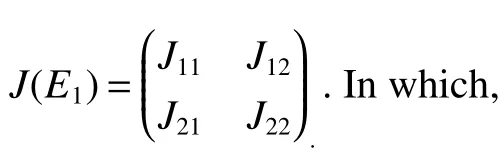
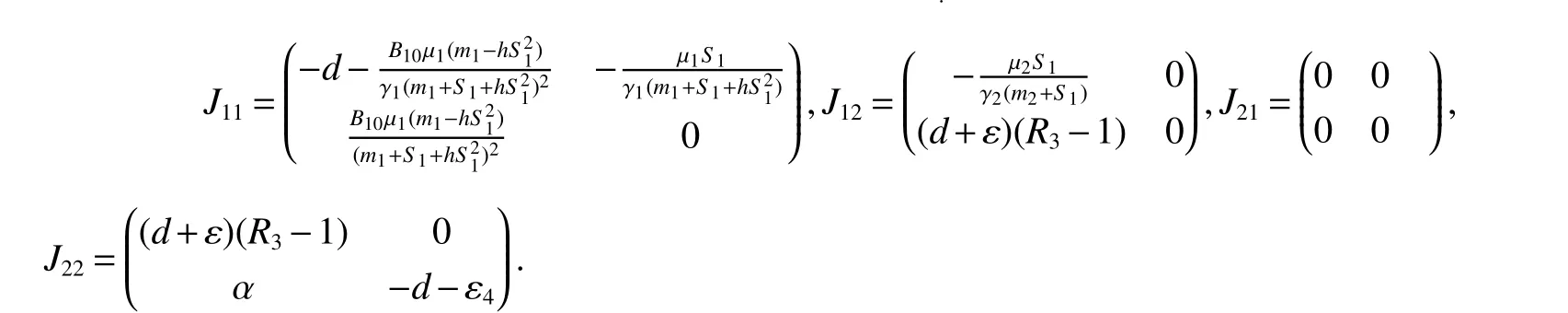
Obviously,det(λE−J22)=0 has two eigenvalues λ1=(d+ε)(R3−1),λ2= −d−ε4<0.If<1,then λ1<0.Sincetr(J11)<0,det(J11)>0.Thus,the eigenvalues ofJ11have negative real part.Therefore,assumption<1 yields local stability ofE1.
Similarly,we can show thatE2is stable if<1.
Theorem 3Assume>1 and<1,and following inequalities hold true:
ThenE2is globally asymptotically stable in the set Ω ={(S,B1,B2,I):S>0,B1≥0,B2>0,I>0}.
ProofWe de fine a Lyapunov function by
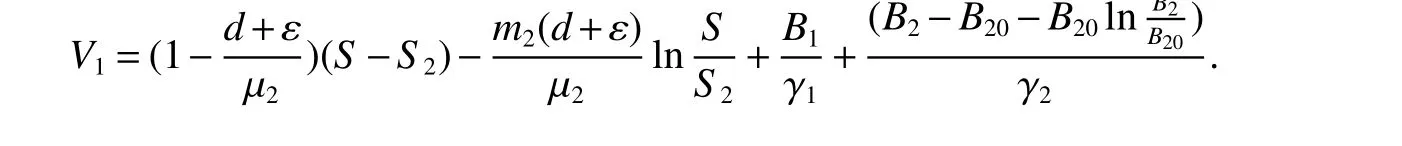
Calculating the derivative ofV1along solutions of(1),we obtain
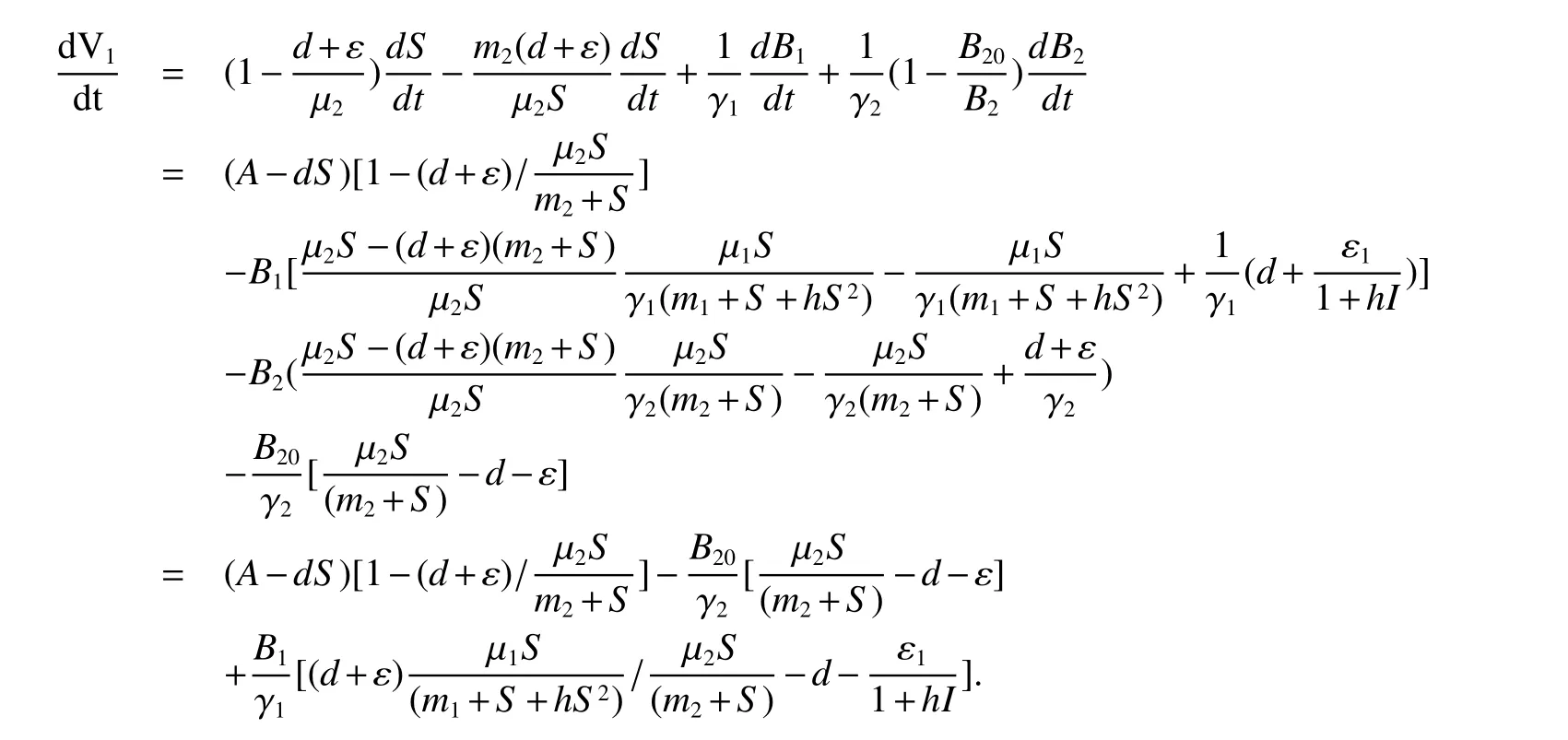
From(4)and(5),together with Theorem 1,we have
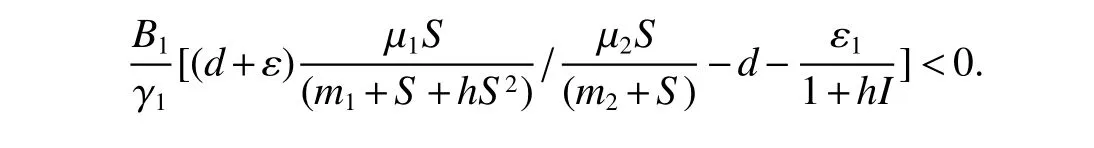
for all large enough t.
Let
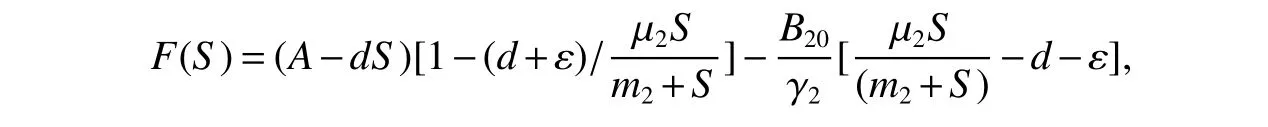
setting

Then
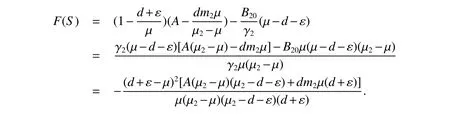
since µ2−µ >0,µ2>d+ε,we haveF(S)<0.Hence,<0.Moreover,it also implies thatF(S)=0 if and only if
Set
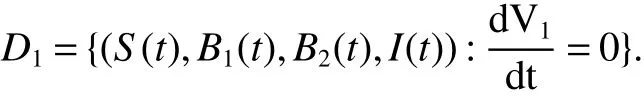

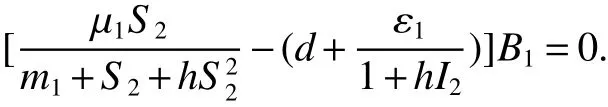
Note that>1 impliesS0>S2.So
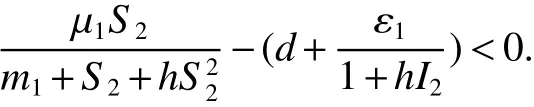
Hence,it leads toB1(t)=0.We further obtainB2(t)=B20,I(t)=I2.Thus,the largest invariant set of(1)contained inD1is{E2}.By the LaSalle theorem,all solutions of(1)in Ω approachE2ast→∞.
Theorem 4Assume>1 and<1.ThenE1is global asymptotically stable in the set Ω={(S,B1,B2,I):S>0,B1≥0,B2>0,I>0}if the following condition holds:
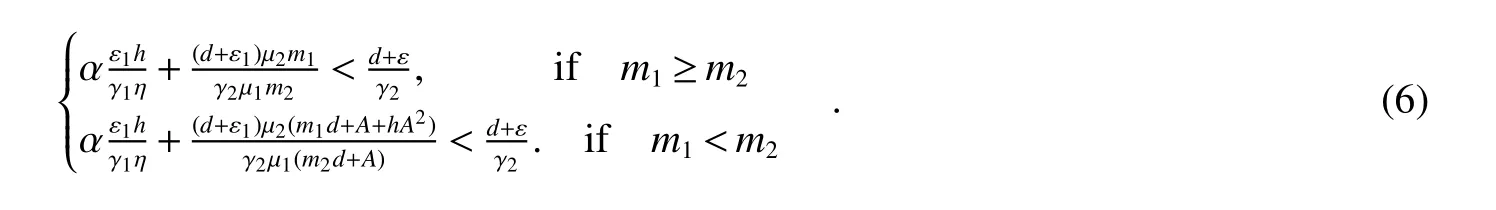
proofFirst we de fine a Lyapunov function by
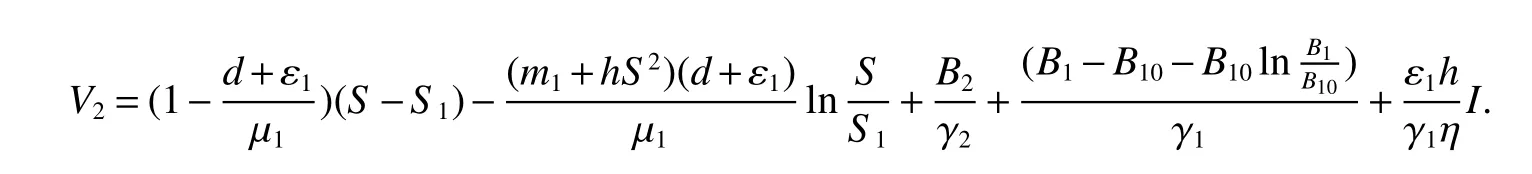
Calculating the derivative ofV2along solutions of(1),we obtain

It is easy to see that(6)implies
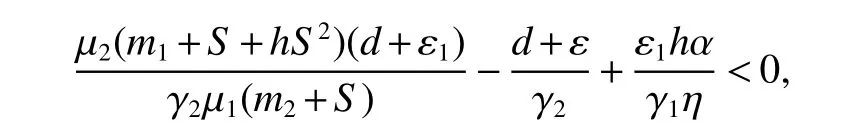
for 0 Let By similar discussions toE2,we see thatG(S)<0,for 0 Remark 1Theorem 3 shows that if the removing rate of the nutrient and bacterial,converting efficiency of nutrition to biomass and maximum growth rate satisfy certain conditions,then the wild type strain to become extinct,and antibiotic resistant mutants and indole will tend to be constant. In this subsection,we will look for conditions under which there exists a positive equilibrium for(1),accounting for co-existence of the two strains. SinceR2>1 yields it follows that populationB2will go extinct ifµ2≤(d+ε).Consequently,the indole populationI(t)is eliminate.So,in the following discussion,we assumeR2>1. Letbe any positive equilibrium of system(1).Then the positive equilibrium point satis fies It is difficult to solve the system(7),so,to be succinct,we suppose that both strains have the same metabolic parameters,i.e.,µ1= µ2= µ,m1=m2=m,γ1= γ2= γ.Thus,from(7)we can get the unique positive equilibrium poinwhere I∗will be positive if and only if Meanwhile,is the unique solution of the system it follows from(9)thatandare positive if and only if Then we have the following theorem Theorem 5Assume that<2>1.If inequality(8)and(10)holds,then there exists an unique positive equilibrium Theorem 6Assume that>1 andIf inequality(8)and(10)holds,thenE∗is locally stable. ProofThe charecteristic equation of system(1)atE∗is Where where ifµ>,then we havea1−d−ε4>0 Sincea1−d−ε4>0,we obtain ∆2>0,∆3>0.Therefore,it follows from the Routh-Hurwitz criteria thatE∗is locally asymptotically stable. References: [1]http://en.wikipedia.org/wiki/Antibiotic-resistance. [2]Bonhoeffer S,Lipsitch M,Levin BR.Evaluating treatment protocols to prevent antibiotic resistance[J].Proc Natl Acad Sci USA,1997,94,12106-12111. [3]Cohen T,Sommers B,Murray M.The effect of drug resistance on the fitness of Mycobacterium tuberculosis[J].Lamcet Infect Dis,2003,3:13-21. [4]Allen A.Katouli and Natalia L.Komarova.The Worst Drug Rule Revisited:Mathematical Modeling of Cyclic Cancer Treatments[J].Bull Math Biol,2011,73:549-584. [5]Stuart B Levy,Bonnie Marshall.Antibacterial resistance worldwide:causes,challenges and responses[J].Nature Medicine,2004,10,S122-S129. [6]Peter A Smith,Floyd E Romesberg.Combating bacteria and drug resistance by inhibiting mechanisms of persistence and adaptation[J].Nature Chemical Biology,2007,3:549-556. [7]Ted Cohen,Megan Murray.Modeling epidemics of multidrug-resistant M.tuberculosis of heterogeneous fitness[J].Nature Medicine,2004,10:1117-1121. [8]D Agata EMC,Webb GF,Horn MA,Moellering RC,Ruan S.Modeling the invasion of community acquired methicillin-resistant Staphylococcus aureusi into the hospital setting[J].Clinical Infect Dis,2009,48:274-284. [9]Patrick De Leenheer,Jack Dockery,TomSs Gedeon,Sergei S.Pilyugin.Senescence and antibiotic resistance in an age-structured population model[J].Journal of Mathematical Biology,2010,61(4):475-499. [10]Andersson DI,Hughes D.Persistence of antibiotic resistance in bacteria populations[J].FEMS Microbiol Rev,2011,35:901-911. [11]Lee HH,Molla MN,Cantor CR,Collins JJ.Bacterial charity work leads to population-wide resistance[J].Nature,2010,467:82–86. [12]Yu P.Closed-form conditionsof bifurcation points for general differential equations[J].Int.J.Bifurcation Chaos Appl Sci Eng,2005,15:1467-1483. [13]Wendi Wang,Xingfu Zou.Modeling the role of altruism of antibiotic-resistant bacteria[J].Journal of Mathematical Biology,2014,68(6):1317-1339.
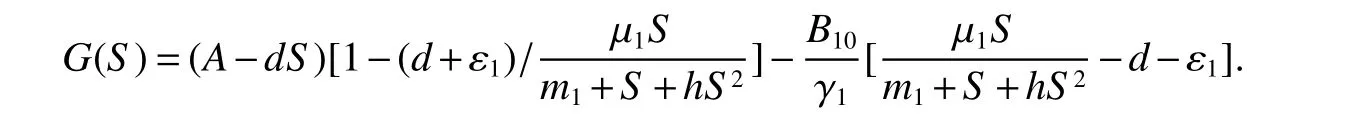

1.3 Existence and Stability of the interior equilibrium
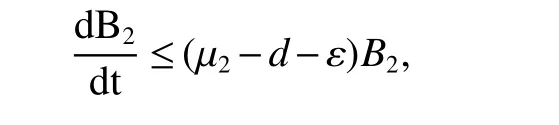
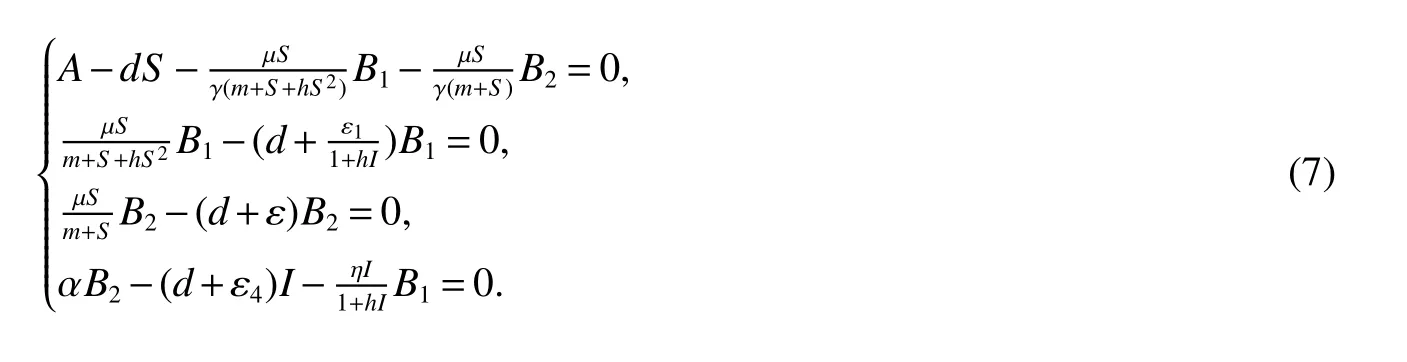


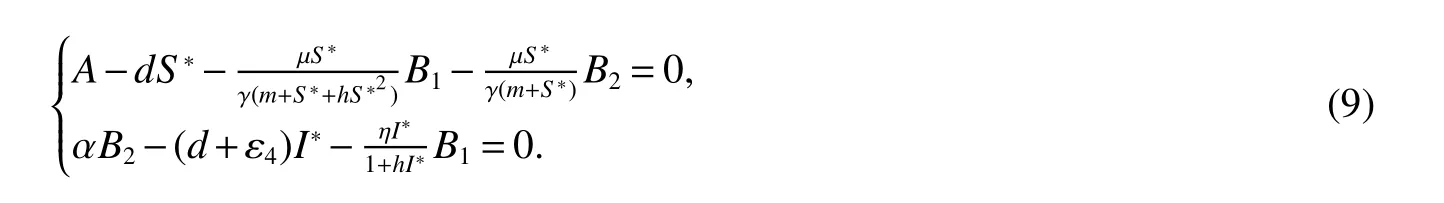

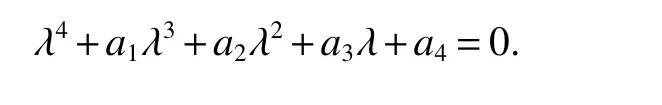


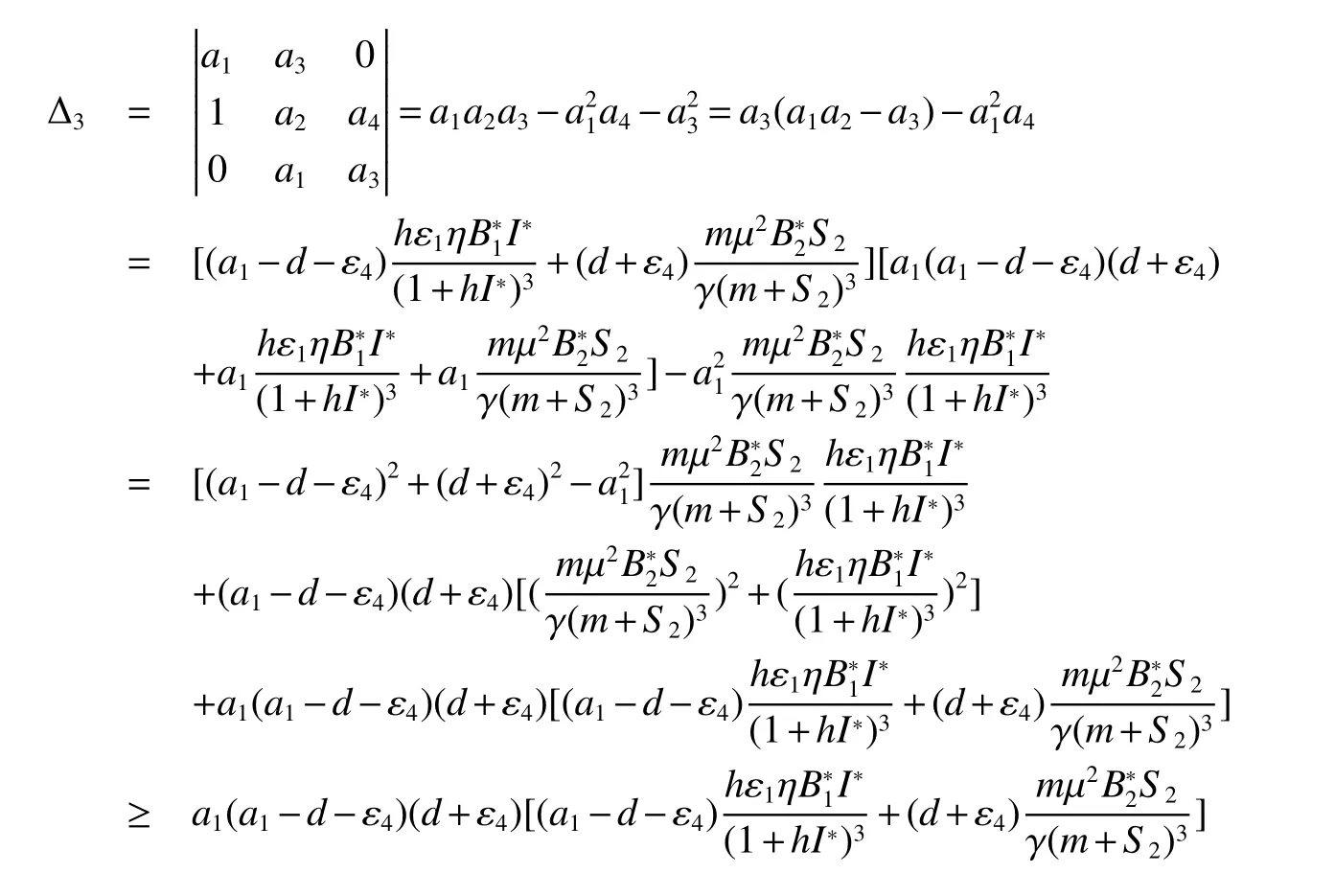
杂志排行
新疆大学学报(自然科学版)(中英文)的其它文章
- WSNs中基于Chebyshev多项式的可认证密钥协商方案∗
- 新疆双峰驼乳清蛋白组分对人宫颈癌HeLa细胞增殖的抑制作用∗
- 新疆加曼特金矿与斑岩型金矿的对比研究∗
- 具有非倍测度的参数型Marcinkiewicz积分交换子在Hardy空间的估计∗
- Periodic Solution of a Two-species Competitive Model with State-Dependent Impulsive Replenish the Endangered Species∗
- Permanence and Extinction for Nonautonomous SIRS Epidemic Model with Density Dependence∗
