利用手工编辑加工函数曲线的宏程序

夏文龙

（广东省工业高级技工学校，广东 韶关512000）

0 前言

目前数控系统没有完善的函数曲线的插补功能，因此实际操作中加工函数曲线的编程多采用手工编辑宏程序来完成，但自动编程加工函数曲线会直接影响到宏知识的传教。作为培养高技能人才的学校，特别是数控教学中根据不同情况，掌握函数曲线的宏编程是非常必要的。现今，数控系统的种类非常多，宏编程的格式有所不一样，但原理一样。宏程序的最大特点是，可以对变量进行运算，使程序应用更加灵活、方便。虽然子程序对编制相同加工操作的程序非常有用，但宏程序由于允许使用变量算术和逻辑运算及条件转移，使得编制相同加工操作的程序更方便、更容易。

宏程序有A、B两类，本人以操作过的数控车床配置的数控系统为例，发现GSK980TD数控系统的数控车床使用的是A类宏程序，相比之下，宏编程的格式繁琐。下面我就以GSK980TD数控系统的数控车床为例，介绍手工编辑加工函数曲线的宏程序。

1 手工编辑宏程序的相关知识

当前的数控系统都为用户配备了较强大的类似于高级语言的宏功能，用户可以使用变量进行算术运算、逻辑运算和函数混合运算。通过它所提供的循环语句、分支语句可大大减少手工编程时繁琐的数值计算，是提高机床性能的一种特殊功能，在函数曲线工件的加工中巧用宏程序将起到事半功倍的效果。

用户宏程序有A、B两类，A类宏程序是以G65 Hm P#i Q#j R#k的格式输入的，而B类宏程序则是以直接的公式和语言输入的，类似于C语言。GSK980TD数控车床中使用的是A类宏程序，它的一般格式为：

G65 Hm P#i Q#j R#k

m：01～99表示运算命令或转移命令功能；

#i：存入运算结果的变量名；

#j：进行运算的变量名1，也可以是常数。常数直接表示，不带#，单位为微米，编程时需乘以1000，转变为毫米；

#k：进行运算的变量名2，也可以是常数。常数直接表示，不带#，单位为微米，编程时需乘以1000，转变为毫米；

指令意义：#i=#jA#k(注：A为运算符号，由Hm决定)。

具体定义看宏指令表（表1）。

表1

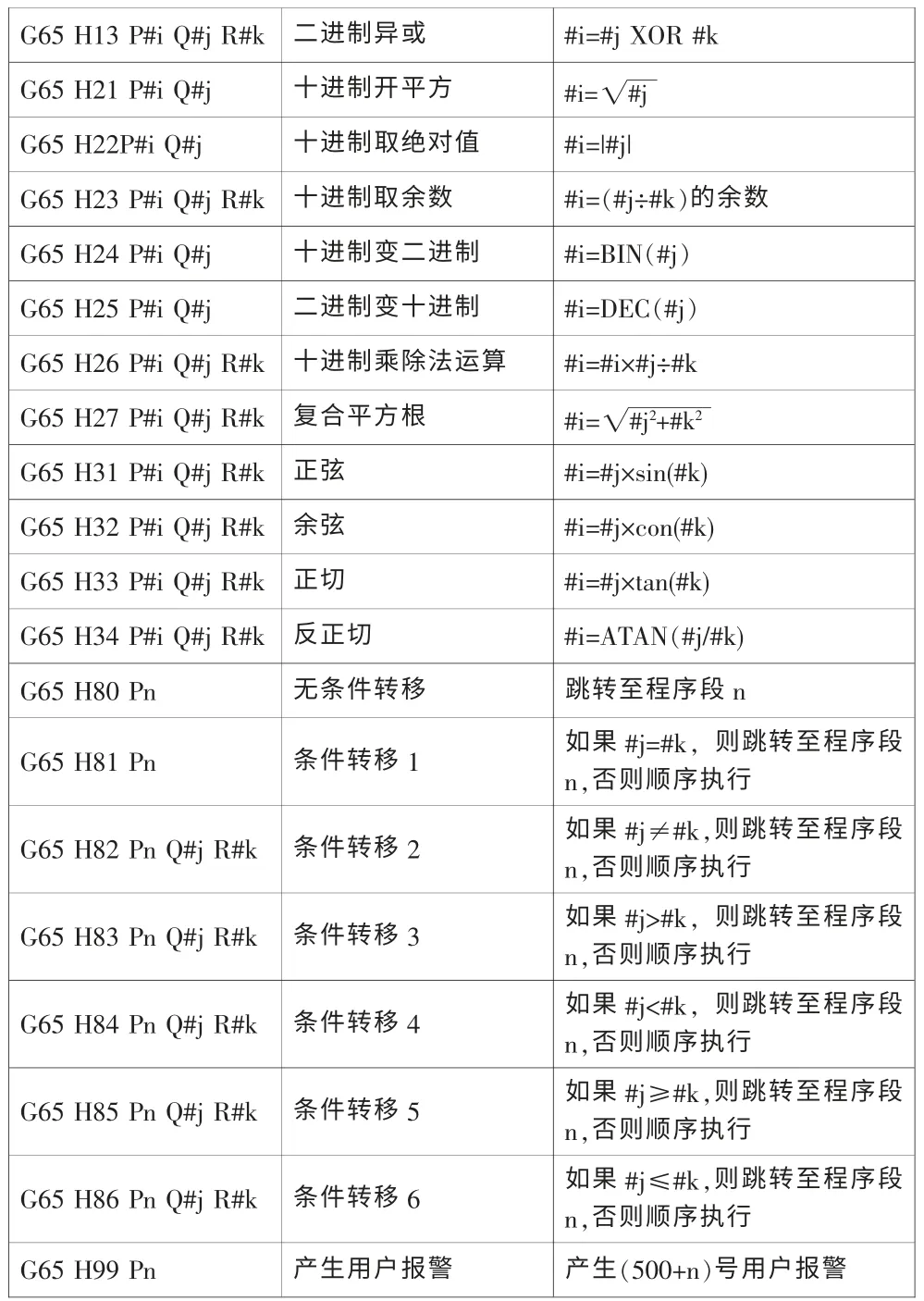
注意：1.用度指定的单位，单位是千分之一度；2.在运算中，当必要的Q、R没指定时。其值作为零参加运算；3.在运算中，小数部分全部舍去，单位为0.001mm.

2 宏编程路径

采用一次性切削的方法来加工函数曲线来编程，在实际加工时，把刀补偏移出来。

其流程图如图1。

3 加工函数曲线的宏程序实例

实例、加工如图2所示的零件，工艺条件：工件材质为45#钢，毛坯为直径Φ50mm，长50mm的棒料。

3.1 正弦曲线图形（图3）

3.2 正弦曲线一般式：y=Asin(ωx+φ)+k，ω=

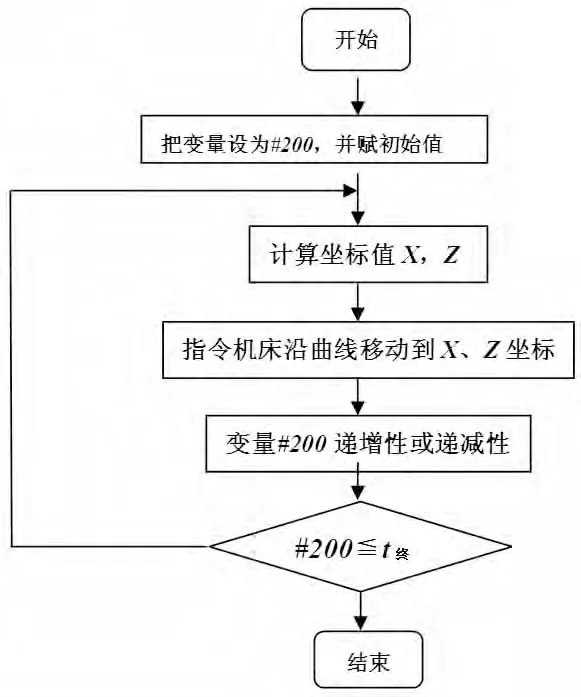
图1

图2

图3

其中：

（1）在直角坐标系上的图象，正弦曲线是一条波浪线；

（2）sin为正弦符号；

（3）x是直角坐标系x轴上的数值；

（4）y是在同一直角坐标系上函数对应的y值；

（5）k、ω和φ是常数（k、ω、φ∈R），ω≠0；

（6）x∈R时定与x轴相交但不一定过（0，0）；

（7）A——振幅，当物体作轨迹符合正弦曲线的直线往复运动时，其值为行程的1/2；

（8）(ωx+φ)——相位，反应变量y所处的状态；

（10）k——偏距，反应在坐标系上的图像为图像的整体上移或下移；

（11）π——代入计算时为180度；

（12）T——周期，半周期是180度，整个周期是360度。

3.3 转换为车床方程：X=Asin(ωZ+φ)+k，ω=

在车床 上加工正弦线时，以Z为变量时，变量的范围确定：Z的变量也就是Z方向的加工起点和加工终点的两个值（正弦线加工起点为Z的变量初始值，一般为0，加工起点到加工终点的距离为Z的变量终止值）。

3.4 加工函数曲线宏程序计算

（1）求出正弦线的方程：车床的方程为X=Asin(ωZ+φ)+k，ω=，正弦线的加工起点直径-正弦线的加工终点直径由图形可以得知，φ的变化是270度到450度，由公式sin(π+α)=-sinα可以得270=180+90、450=360+90，也就是说明sin270与sin90成正负关系，在计算X值时只能正值，那就是用sin90代理sin270，然后在Z的值添加负号，sin450与sin90相等关系；K为42，即偏心距；T的值是正弦线从270至450，只变化180度，此时为半个周期是14，整个周期是28；加工起点是在正弦线的轴线最高点，正弦线的编程方程为：，X为直径值。

（2）变量的确定：以Z为变量，变量范围[0,14]，计算方法是加工起点为0，加工终点是正弦线的起点到终点的距离。3.5 加工函数曲线宏程序（表2）

表2

4 结束语

用手工编辑宏程序可以在数控车床上进行函数曲线的插补，弥补了数控系统中没有函数曲线插补功能这一不足。编辑程序时，可参照其数学公式、微分方程等有关知识，使编程计算大大简化，程序的可读性强，提高了编程效率，从而充分发挥数控机床的内在潜力，提高加工效率和质量，同时使宏知识在学校得到广泛是学习和应用。作者通过多次实践证明，加工函数曲线用手工编辑宏程序能高效、准确地加工出正弦线的轮廓。（说明：至于余弦线曲线的宏编程在此不一一编辑）

［1］广州数控设备有限公司.GSK980TD车床CNC使用手册[M].

［2］冯志刚.数控宏程序编程方法、技巧与实例[M].机械工业出版社,2007.