泛布尔代数在航空维修效率评价中的应用研究

李威李彬

（武汉理工大学自动化学院，湖北 武汉430070）

0 引言

随着科学技术的快速发展，航空工业日新月异,航空体系日趋复杂,为适应航空装备复杂多变的使用需求，发挥出航空装备的最大功效，必须实施航空维修的科学管理。维修人员作为维修保障资源的关键要素，是装备维修活动中的主体，也是最积极、最活跃的因素，在装备维修保障中发挥着至关重要的作用。科学合理地制定航空维修效率评价系统，对于维修保障工作具有重要的现实意义。时间就是生命，维修效率的高低就成为航空装备发挥功效的重要因素。一方面可以科学合理的评价航空维修工作效率；更重要的是通过评价系统，可以衡量装备系统当前实际的维修能力和水平，掌握与期望能力之间存在的差距。

1 基于泛布尔代数的航空维修效率评价系统

1.1 航空维修

航空装备是航空器及其各种装置、设备的统称，通常指飞机、直升机、航空发动机、航空军械、航空电子设备以及航空仪表、电器设备等；《GJB451-2005可靠性维修性保障性术语》认为维修是使产品保持或恢复到规定状态所进行的全部活动；航空维修是指保持、恢复、和改善航空装备规定技术状态而在航空装备寿命周期过程中所进行的一切工程技术和管理活动[1]。

航空维修活动对航空装备（主要指飞机，下同）的影响极大，它是使飞机保持或恢复到规定状态所必需的基本维修作业。由于大量新技术在航空装备上的使用，飞机的可靠性和安全性得到很大的提高，因使用不当或设计生产阶段的缺陷导致的事故发生的机率逐渐变小，于是地面的维修活动逐渐成为影响飞机发挥系统效能的主要因素。

1.2 效率评价

随着经济的发展,效率成为经济学中最有吸引力的概念之一。萨缪尔森在《经济学》中写道：“效率意味着不存在浪费,也就是说,当不降低一种商品的生产就不会增加另一种商品的生产时的经营将是有效的。”在这里,抛开其哲学意义和经济内涵,这个概念应该存在于人们选择行为的现实情况中。当人们面对资源稀缺时,自然会选择“效率”的概念,因为人们总是希望最大限度地发挥“实用”。航空维修机组人员在维修单位中属于最基本的维修单元和实际操作者，是影响飞机空中效能实现的重要因素，其工作的有效与否势必使得飞机系统的效能存在差异[2]。

分析现状，飞机的系统效能受到设计人员、生产人员、使用或操作人员、维修人员和保障人员的影响。一线机务维修活动有效与否，一线维修人员的工作将直接影响飞机系统效能。将效率这一概念进行拓展，在航空维修中建立维修效率评价系统具有重要的现实意义。

1.3 泛布尔代数理论

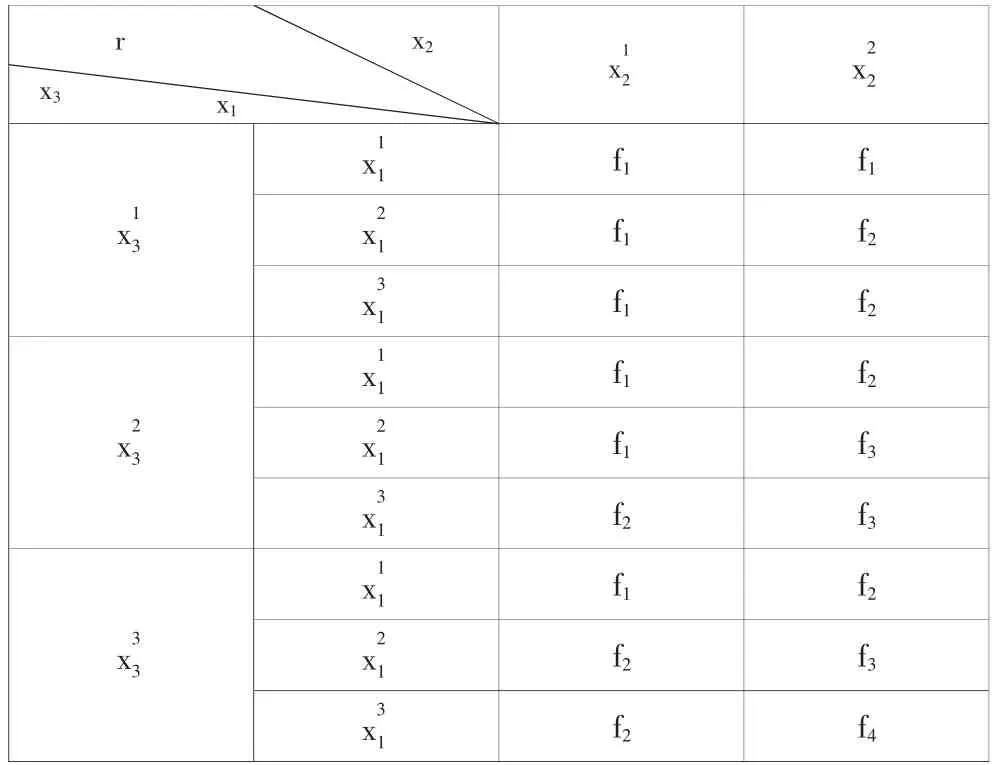
泛布尔代数的数学模型是建立在输出、输入因果联系基础上的模型,即逻辑模型。泛布尔代数的基本思想是,若令符号x1,x2,x3,…,xi表示多状态系统中的诸变量,且把其中任一变量xi所可能出现的所有状态的总数称作相应于xi的“状态数”,并以ni(i=1,2,…)表示。又以xji(i=1,2,…;j=1,2,…,ni)表示相应于xi的第j个状态,称为xi的“状态变量”,即当第j个状态出现时,取为1值,而当第j个状态不出现时,则取为0值。在多状态系统中,每个变量xi在某一确定的场合,取且仅取ni个状态中的一个状态,这就要求其同时满足以下2个条件：①x1i+x2i+…+xji=1；②xji·xki=0(1≤j

可见泛布尔代数提供了一套相对简单的数学方法,从数学上严格区分数据的每个状态值,每个状态值都有唯一的泛布尔的表达式,没有遗漏值也不会有重复值；可以描述系统的决策规则,能应用其公理体系对决策规则进行相应的简化,并得到最简的决策规则模式。

2 数学模型的建立

选定合情合理的考评指标对维修系统进行考核和评估是装备形成战斗力的重要环节。一方面可以衡量装备维修系统当前实际的维修能力和水平，掌握与期望能力之间存在的差距。更重要的是能进一步确定当前系统存在的薄弱环节，为后续能力提升提供改进方向和依据[4]。

在维修现场要评估维修效率，实际上就是评估维修机组人员的效率。结合实际工作经验，通过归类、整理、分析，并且能够明确表示，本文初拟了判定航空维修效率的几个因素：排除故障总时间X1、维修卡片填写质量X2和参加排除故障人数X3，通过这三个因素来判定此项维修工作的效率低、正常或者高。并且确定如下准则：排除故障总时间越长效率会越低，维修卡片填写质量不合格效率会越低，参加排除故障人数越多效率也会越低。

参照泛布尔代数理论体系,可以建立该系统的泛布尔控制模型。三个因素的状态数分别为n1=3，n2=2，n3=3，即x11（排除故障总时间长）x21，（排除故障总时间正常），x31（排除故障总时间短），x12（维修卡片填写质量不合格），x22（维修卡片填写质量合格），x13（参加排除故障人数多），x23（参加排除故障人数正常），x33（参加排除故障人数少）组成系统全部输入状态变量。另外，用F表示输出变量，状态数为4，即f1（效率低），f2（效率正常），f3（效率较高），f4（效率高）。

根据控制规则，有如下3×2×3=18种实际情况，（1）输入时输出输入时输出f1，（3）输入时输出f1，（4）输入时输出f2，（5）输入时输出f1，（6）输入时输出f2，（7）输入时输出f1，（8）输入时输出f2，（9）输入时输出f1，（10）输入时输出f3，（11）输入时输出f2，（12）输入时输出f3，（13）输入时输出f1，（14）输入时输出f2，（15）输入时输出f2，（16）输入时输出f3，（17）输入时输出f2，（18）输入时输出f4。

该系统逻辑图表示如下：

根据逻辑图中的函数关系可以得出以下控制表达式：

排除故障总时间X1的确定：飞机交接给维修人员为时间起点，维修人员将飞机交出为时间终点；维修卡片填写质量X2的确定：按照维修卡片填写规范判定；参加排除故障人数X3的确定：机上操作都有严格的工卡流程，每一项工作都要签字确认，X3以实际签字人数为准。由此可见，对于实际工作中任何一种维修状态，这三个因素都是独立的可以明确评判的，都能通过泛布尔代数的数学描述，建立确定的可解释的模型，最终得出科学的一目了然的效率评价。

3 结束语

对于任何一项维修工作，X1、X2、X3都是唯一确定的，依据这种数学模型中的量化关系,很容易转化到软硬件中实现控制功能。通过相应的控制规则，每一项工作的效率F都是确定的，用事实和数据说话，相比于以前的主观评价更加具体、科学而且有说服力，也从一定程度上解决了维修现场效率评价随意性大、主观性强的问题。

飞机是一个复杂而庞大的系统，笔者曾经维修的飞机部（附）件就达到一千多个，各个系统排除故障总时间和参加排除故障人数的参考数值是不同的，本文仅提出了一种可供判定效率的理论方法，应用到实际还需要大量的调研和数据统计，这是随后的研究重点。

［1］郑东良.航空维修管理[M].北京：国防工业出版社,2006.

［2］郭定.航空维修工效学[M].北京：国防工业出版社,2007.

［3］张南纶.泛布尔代数公理体系[J].空军气象学院学报,1985(1)：338-353.

［4］Neely A,Gregory M,Platts K.Performancemeasurement system design：a literature review and research agenda[J].International Journal of Operations&Production Management,2005,25(12)：s1228-1263.