基于拉格朗日乘子的三维位场约束反演方法

张 毅李 斐鄢建国李 辉湖北省地震局地震大地测量重点实验室，武汉 430071武汉大学测绘遥感信息工程国家重点实验室，武汉 430074

基于拉格朗日乘子的三维位场约束反演方法

张 毅1,2）李 斐2）鄢建国2）李 辉1）
1）湖北省地震局地震大地测量重点实验室，武汉 430071
2）武汉大学测绘遥感信息工程国家重点实验室，武汉 430074

一般来说，地球物理数据是地下物质某种物性参数在特定空间中的响应，而地球物理反演正好相反，它是通过获得不同的模型参数估计来拟合实际观测数据。由于地下模型参数网格个数通常远远大于观测数据个数，反演方程通常是欠定，反演结果并不唯一。通过在模型目标函数中添加最小模型及最平缓模型的限制，构建L2范数条件下的反演方法，解决了反演问题中解的非唯一性问题。

其中，w(z)为深度加权函数。在位场反演的过程中，由于该函数随深度的迅速衰减，会产生类似电场中的“趋肤效应”，即反演结果基本趋向集中于地表。为了克服这种效应，Li & Oldenburg（1996, 1998）引入了深度加权函数，用来近似地补偿核函数随着深度的衰减。

实际观测数据中通常都含有一定的噪音，这些噪声既可能来源于采集时仪器或者人工误差，也可能来自数据后处理过程中的误差。因此，定义一个合理的评价数据的误差数据目标函数，即数据拟合差是十分有必要的。

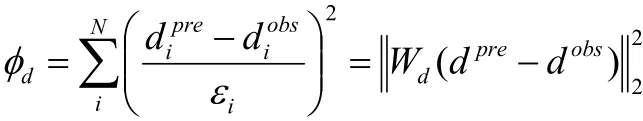
利用Tikhonov正则化理论构建反演目标函数：min：φ（m）=φd+μφm，其中μ为Tikhonov正则化参数。对反演目标函数求最小值

在实际地球物理反演过程中，通常会有大量的地质、地球物理等先验约束信息。通过拉格朗日乘子法，可以构建约束条件下的三维位场数据反演目标函数，使物性分布特征等先验信息可以添加进反演过程之中。此时，反演过程还需要满足如下关系式：

引入拉格朗日乘子、松弛变量以及惩罚函数，并求取最小值可以得到：

通过拉格朗日乘子法中约束项的引入，使反演目标函数得到适当扩展，重新构建了新的三维位场反演的目标函数，由于各种先验信息在反演过程中的使用，会在一定程度上对反演结果起到“聚焦”的作用，同时也更加符合实际情况。