低空安全监测飞艇介绍及其行驶路线问题研究*

李延武，苏国锋，袁宏永

（清华大学工程物理系公共安全研究院，北京100084）

低空安全监测飞艇介绍及其行驶路线问题研究*

李延武，苏国锋，袁宏永

（清华大学工程物理系公共安全研究院，北京100084）

在地震救灾中，利用低空安全监测飞艇进行灾情监测是了解灾情的有效手段。由于飞艇信号传输具有距离限制，如何结合救灾需要和飞艇技术参数提前设计飞艇的行驶路线是一个急需解决的问题，同时也是飞艇救援指挥系统的重要组成部分。该文首先介绍了低空安全监测飞艇的优势和功能，然后结合应急救灾实际情况，将低空安全监测飞艇的路线问题转化为带条件的旅行商问题，并通过仿真实验详细分析比较了蚁群算法、“最近邻居”算法、模拟退火算法、遗传算法四种算法在解决该问题时的效果。结果表明，蚁群算法得到的最优解次数最多、计算时间最稳定，于是将蚁群算作为原问题的核心算法，提出了该问题的解决方案。

地震救援；灾情监测；安全监测；飞艇；行驶路线；旅行商问题

在地震救灾中，如何尽快了解灾区损失情况，从而合理、有效地分配救灾力量是一大难题。在2008年汶川8.0级大地震中，交通网、通信网等被破坏，直升飞机不能得到清晰、稳定的路面图象，卫星的实时操作性较差，使得决策者不能根据损失情况进行资源调度、分配救援力量。缺少实时有效的监测手段，已经成为地震应急的瓶颈问题。

为了解决这一问题，清华大学研制了低空安全监测飞艇（图1），将3S技术（GIS、GPS和RS技术）［1］和飞行控制技术相融合，利用飞艇将地震灾区低空区域的图像、相关环境参数和灾害产物参量和参数进行多维自动采集、处理后，通过无线方式将采集各种参数传输到监测中心。该系统同时适用于地震灾害监测评估、环境监测评估、火情监测评估、通信中继、集会监测、日常和应急巡查、应急物资投运等应急情况，具有广泛的应用性。

图1 低空安全监测飞艇系统（待起飞状态）

低空安全监测飞艇属于无人操作系统，需要通过航线设置系统在二维GIS地图设置航线，飞艇将自动按照预设航线执行飞行任务。由于应急过程时间紧、任务重，如何尽快选择合适的路线是直接影响到应急效果的重要问题。同时，为了提升飞艇的智能化设计，路线算法应该尽量快速，且便捷、所耗资源要少，为飞艇飞行过程中的路线自动计算与调整提供技术可能性。

1 低空安全监测飞艇介绍

低空飞艇安全监测技术已广泛应用于电力巡线、人员搜救、灾害监测、环境监测等方面［2］，相比于卫星遥感、航空遥感和无人机遥感等技术而言，飞艇监测技术具有以下几点优势［3］。

（1）覆盖范围大。覆盖最长距离为10～100 km，接近卫星、航空遥感的覆盖范围，高于无人机的监测范围，特别适合于造成现场道路和交通遭到破坏的区域以及人员无法进入的高危险区域的安全监测，如地震灾区的监测任务。

（2）高空间观测精度和分辨率高。随着视频跟踪［4］和稳像技术［5］的发展，飞艇监测的分辨率可以达到厘米量级，高于卫星遥感，其稳定性高于一般的航空遥感，能够满足安全监测的需求。

（3）可扩展性强。由于低空飞艇有较强的载重能力，可以根据灾害应急的需要搭载辐射监测、空气监测等各类专业监测装置，甚至进行应急物资的投放，其应急可扩展性是无人机等轻型设备所无法比拟的。

（4）成本较低。相比于卫星遥感和航空遥感而言，低空安全监测飞艇的数据成本和系统建设成本较低，易于保养、修复，适合复杂环境使用。

清华大学研制的低空安全监测飞艇包括动力飞行部分、视频监测与投掷系统部分以及无线传输部分三个部分，可以在事件发生后快速抵达现场，完成现场信息（图像、地理信息、环境参数等）采集、传输处理，实现事发现场空地立体监测。其主要功能模块包括有4种。①自动导航与预先设置功能：可自动定位导航飞行到制定地点，指挥人员可通过PDA、PC等多种手段进行遥控指挥，可根据设置的任务点自动执行预先设置的任务。②智能扫描与远程监测功能：能利用GIS、GPS、RS、电子罗盘定位、航空摄影空间解析模型实现地物目标监控图像与地物GIS位置的双向智能自动扫描，将高空采集的现场图像和高清晰照片传送回指挥中心。③远程投掷功能：可远程定点投掷多参数传感器，进行现场采集，可以实现温度、湿度、环境气压、风向、风速等环境参数和硫化氢、氢氰酸、氨气等有毒气体的信息采集，亦可以投掷少量应急物资。④中继功能，可对现场图像、语音、数据进行中继传输，保证远端指挥中心实现接收现场采集的各种参数。

2 问题描述

结合飞艇的实际技术参数，低空安全监测飞艇其路线选择问题描述如下。

（1）路线要求：飞艇必须从起飞点起飞，巡航完毕后到起飞点降落补充燃料；应急监测情况下，需要首先探测一些重点地域（交通枢纽、供电站、核电站、居民密集区等），飞艇需不重复地经过每一个重点领域进行巡航，同时为了巡航到更多的地域，飞艇需要走最短的路线；飞艇的起飞点必须是正常交通工具可以达到的，因此可能与探测点有较远的距离，如果存在不能覆盖所有重点区域的情况，需要另选起飞点进行。

（2）飞行控制要求：飞艇可遥控距离仅1.5 km，1.5 km外靠飞艇GPS路线自动识别系统完成，在地面形式恶劣的情况下无法人工更改预设路线。

（3）相关参数计算：飞艇飞行相对高度1 000 m，抗风等级5级，可以认为是直线运行。飞艇摄影偏角平均值5°，以高度1 000 m计算得单次摄影范围半径87.48 m，按照技术标准，地图150 m距离内的测试点可认为是一个点，即地图分辨率为150 m；飞艇发动机总功率20×2 hp（双发动机），续航时间4 h，巡航速度45 km／h，最大飞行速度72 km／h。考虑每次上升、下降时间，一次巡航最大距离不超过150 km。

3 问题分析与模型建立

3.1 旅行商问题简介

旅行商问题（Traveling Salesman Problem，TSP）是最基本的路线问题。其简单表述如下：一个商人欲到n个城市推销商品，每两个城市i和j之间的距离为dij，需要选择一条最短路线，使得商人在每个城市走完一遍后回到起点［6］。

3.2 问题分析与转化

原问题在形式上近似TSP问题，属于NPH问题，可以先向TSP问题转化，再利用启发式算法求解。原问题中有三点与传统TSP问题的不同之处进行分析处理。

（1）多个起飞点的可能：考虑到现实情况下基本上是进行城区或县域的监测，北京五环全长约为99 km，已经远远大于一般的县城区，因此可知150 km的巡航距离基本能够满足巡航的要求。如果出现极个别的区域覆盖需要（例如核电站经常放在偏远区域），可以单独考虑。这里，可以在GIS上根据起飞点和主要的探测区域画一个边长为10 km的正方形作为主要研究区域，在正方形外的点基本可以作为第二点选择。

（2）总长度的限制：在起飞点最佳的基础上，如果总长度超出，可以去掉与起始点最近的点进行计算（去掉的点数从1到n依次递增），直至出现符合总长度的路线。剩下的点进行同样方法的二次迭代。

（3）地图分辨率：将距离为150 m的点取其重心作为一个点进行分析。

经过以上的处理，该问题就可以简化成有限制的TSP问题［7］，数学模型如下所示。其中xij＝1表示商人行走路线包含从城市i到城市j的路径，反之xij＝0表示没有包含。dij为城市i和城市j之间的距离，S为满足要求的任意集合，｜S｜表示集合S元素的个数，T为最长路径限制。

4 算法设计与实现

4.1 算例估算

首先进行数据估算。以北京市海淀区为例，海淀区共有人口密集区22个（西苑、羊坊店、六郎庄、中关村、唐家岭、肖家河、万寿路、八大处、14所密集的大学），能源供应地点3个（供电、供水、暖气），其他重要交通枢纽3个（西直门、车公庄、甘家口），一共28个观测点，大学占了很大的部分。一般的城市大学这种特殊密集区较少，因此这里取20个观测点为一般的城区观测对象是合适的。

假设已经进行了前期的数据处理（分辨率和区域划分处理），还剩20个观测点，问题属于传统TSP问题，这里随机生成10个算例，保证其两点距离大于150 m，进行计算。

4.2 算法设计

本问题中，20个观测点路线选择有（N-1）！／2＝6.08×1016种方法，使用枚举方法计算量巨大，不适合应急救灾的突发情况，需要采用启发式算法进行计算。以下将采用常用的蚁群算法、“最近邻居”算法、模拟退火算法、遗传算法四种启发式算法进行计算，均使用最佳参数设计，并比较其计算结果。

4.2.1 蚁群算法设计与参数选择

蚁群算法（ASA）由意大利学者M.Dorigo等人首先提出，是一种基于群体智能的算法，模拟蚂蚁在寻找食物过程中依靠信息素来进行通信的行为［6］。不同的地区分布着不同的蚂蚁，每个蚂蚁的位置构成一个解集。在每条路径上设置初始的信息量，当蚂蚁按照一定概率转移时，计算蚂蚁走过的路程并改变轨迹的强度，当循环计数小于预定的最大迭代次数且不退化时，则得到最优结果。［8-9］。

用蚁群算法求解TSP问题的运行效果受到信息素重要程度参数α、启发式因子重要程度参数β等参数的影响，其合理取值范围为［0，5］。参数ρ的影响在于其体现的蚂蚁留在其通过路径上信息素的挥发性，一般取0.1～0.2比较合适。信息素增强强度系数Q对结果影响不大［10-11］。基于对蚁群算法参数最优化的比较分析，最终取最大迭代次数NC＿max＝200，蚂蚁数为30，信息素重要程度的参数α＝1，启发式因子重要程度的参数β＝5，信息素蒸发系数ρ＝0.1，信息素增加强度系数Q＝100。计算打印出最优路线、L-best（各代最优路线长度）和L-ave（各代路线的平均长度）。计算结果如图2所示。

4.2.2 “最近邻居”算法设计与参数选择

最近邻居搜索算法（NNS）的定义是：有一个待查询的点q，在点集P上构造一个数据结构，利用该结构可以在一个已定义好的距离向量上找到距离q点最近的点p［6］。最近邻居搜索算法是基于分割原则实现的，其首要是要选择分隔空间的参考点，可以很容易地构造一个平衡二叉树，它以参考点为结点，以数据为叶结点。此后的算法遵循“单个碰撞原则”［12］，即假定：如果两条记录数据是相同的，那么它们获得至少一次碰撞相同数据段的机会就会相对高很多［13］。

根据“最近邻居”算法的定义，设置参数：人口规模pop＿size＝20，地区规模N＝20，判断是否画迭代次数图的逻辑函数show＿prog＝1，判断是否输出最短路线图的逻辑函数show＿res＝1。计算结果见图3。

4.2.3 模拟退火算法设计与参数选择

模拟退火算法（SA）的思想最早由Metropolis等提出的，其出发点是基于物理中固体物质的退火过程［6］。先根据各地区距离矩阵计算出一个初始温度，在内循环中随机选择一个路径，计算新旧路径的长度差，在外循环中计算下降后的温度，当到达“零度”时结束计算，否则一直重复。模拟退火算法寻找的最优解与初始点的选择无关［14］。

基于对模拟退火算法参数最优化的分析，本案例中地区数N＝20，对应MAPKOB链长度为100N＝2 000，对应的最优参数［15］如下：温度下降参数K＝0.95，地区数N＝20，零度标准T（K）＝0.01。在计算结果中用*标示初始地区，途经地区依次用方块标示。计算结果见图4。

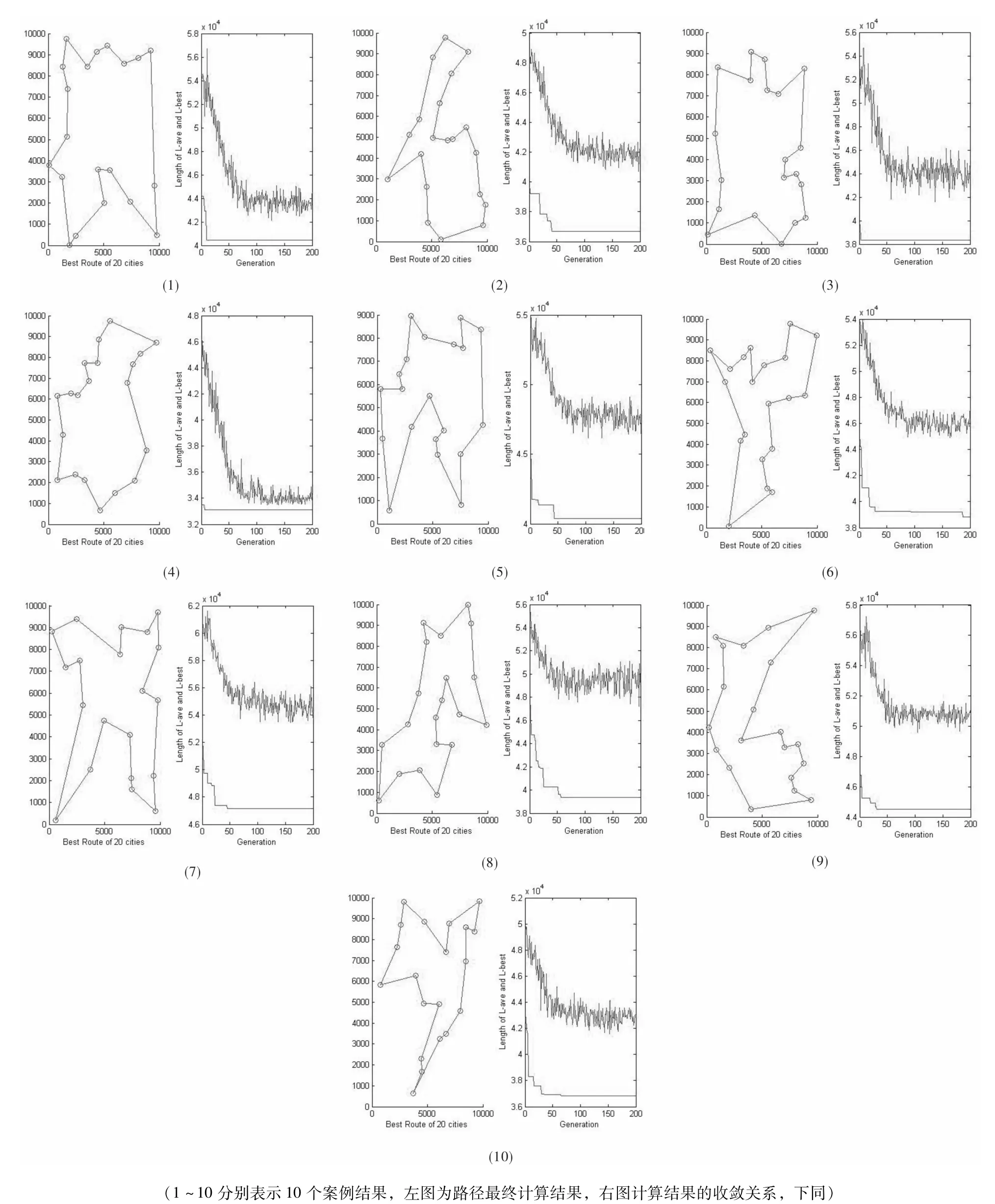
图2 蚁群算法计算结果

4.2.4 遗传算法设计与参数选择

遗传算法（GA）是由生物界的进化规律演化而来的算法［6］。其对算法所产生的每个染色体进行评价，计算每个个体的适应度，并由此选择染色体，在选择计算中保证适应性好的染色体有更多的繁殖机会。将地区之间的距离记录，进行迭代计算，每一代用轮盘赌的方式竞争选择染色体，通过交叉计算实现继承，用基因的随机排序实现染色体的变异，当迭代次数大于迭代总代数时停止运算。［6］

遗传算法的主要参数为截止代数［16］。经过试验，取截止代数为5 000即可得到最优解，同样，设置地区数N＝20。在计算结果中用*标示初始地区，途经地区依次用方块标示。计算结果见图5。

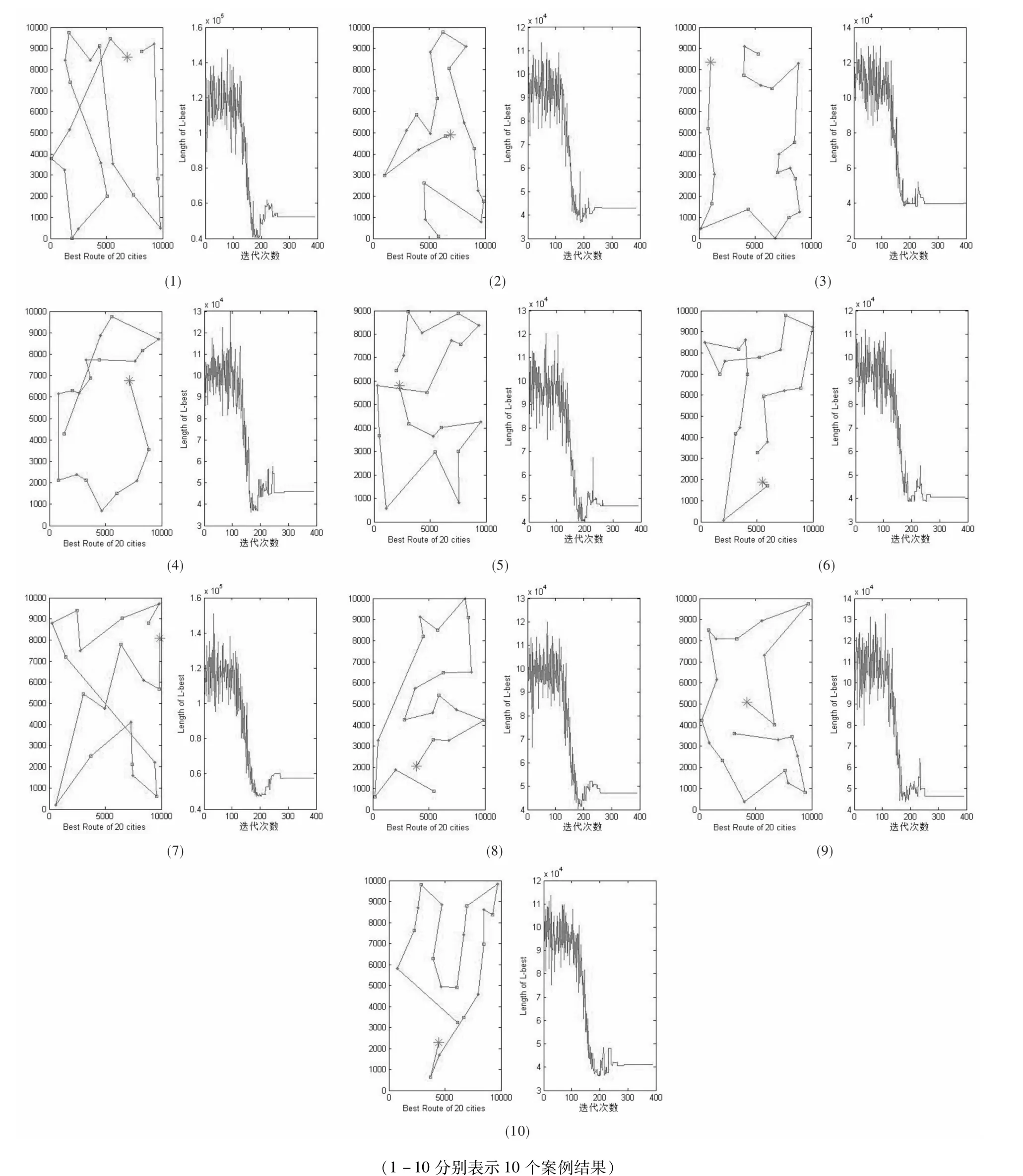
图4 模拟退火算法计算结果

5 计算效果比较

实际救灾中使用的算法，需满足准确度高、耗时少的要求，才能适应应急救灾的需要。十个案例的计算结果（近似到整数，单位为m）比较如表1所示，相对最优解已经用黑体标出。可见ACA算法得到最优解的次数最多，之后依次是GA算法、NNS算法和SA算法。为了模拟实际情况，四种算法均在家用笔记本电脑上进行计算（主频2.5GHz，内存4G），尽量保证计算环境相似，计算所需时间比较见表2（单位为s）。四种算法在家用笔记本电脑上计算所需时间均在10s以内，既能满足在飞艇出发前计算预设路线的时间要求，也能节省飞艇在高空进行飞行路线计算和调整的时间成本。计算其标准差、平均值及变异系数见表3，得知变异系数ACA＜NNS＜SA＜GA，因此ACA算法计算所需时间最稳定。

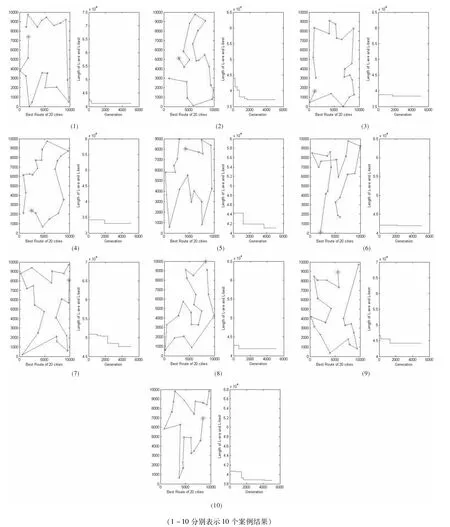
图5 遗传退火算法计算结果

综上比较，结合算法稳定性需要和最优解结果，ACA算法最适合做低空安全监测飞艇行驶路线的算法。

6 算法总结

经过前面的比较，证明ACA算法适合解决本问题，因此，原问题处理流程设计如图6所示。

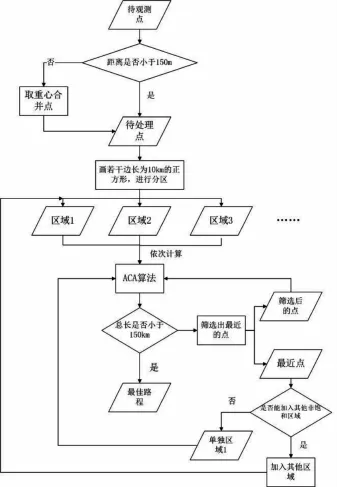
图6 低空安全监测飞艇行驶路线解决方案

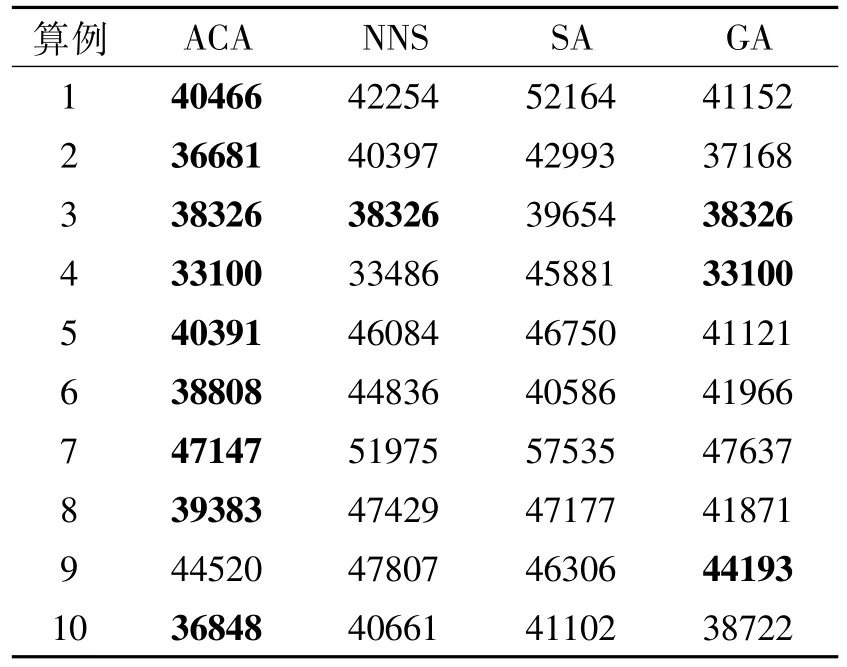
表1 四种算法计算10个案例结果比较

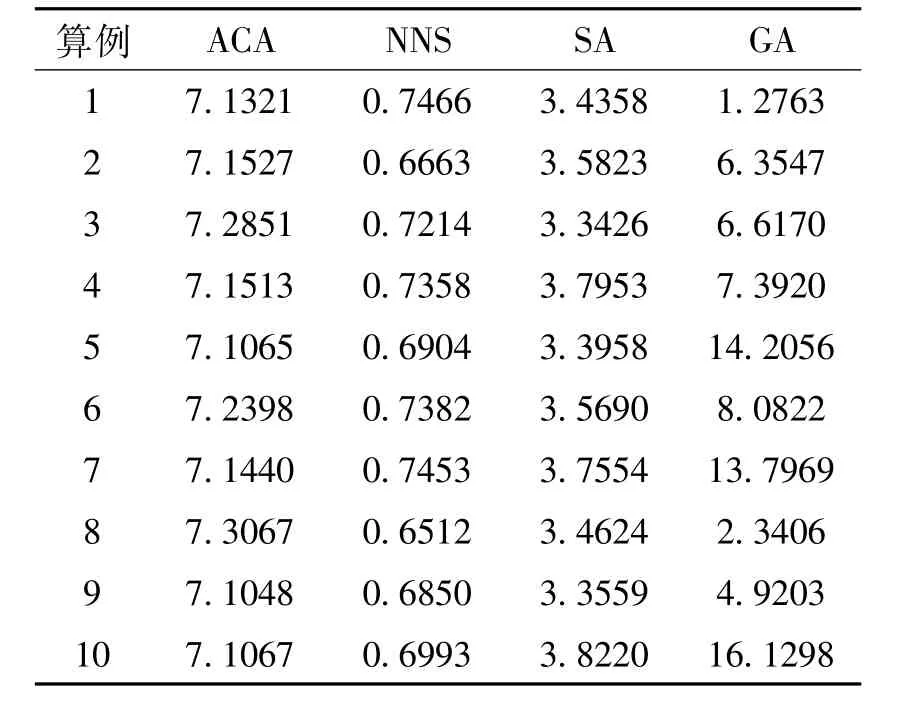
表2 四种算法计算10个案例所用时间比较

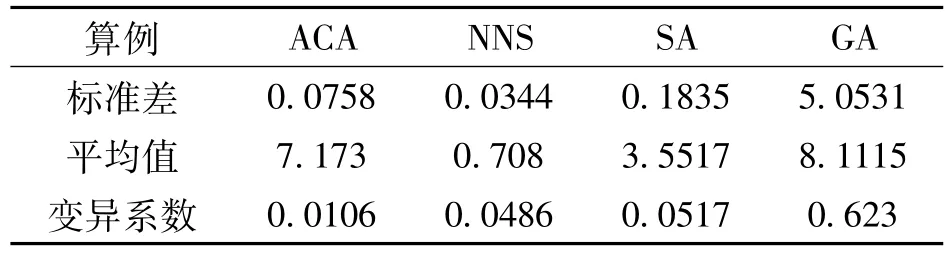
表3 四种算法计算10个案例所用时间比较分析

7 结语

本文首先介绍了低空安全监测飞艇的优势和功能，然后结合应急救灾实际情况，将低空安全监测飞艇行驶路线问题转化为总路程限制的旅行商问题，再详细讨论了蚁群算法、“最近邻居”算法、模拟退火算法、遗传算法四种算法对原问题处理结果的比较，最终确定蚁群算法作为解决问题的核心算法，从而提出了原问题的解决方案并得到应用。

［1］ 李剑萍.3S技术在灾害监测预测中的应用及展望［J］.灾害学，2004，19（Supp.1）：83-87.

［2］ Hain JHW.Lighter-than-air platforms（blimpsand aerostats）for oceanographic and atmospheric research and monitoring［C］／／OCEANS 2000 MTS／IEEE Conference and Exhibition.IEEE，2000，3：1933-1936.

［3］ 李云，徐伟，吴玮.灾害监测无人机技术应用与研究［J］.灾害学，2011，26（1）：138-143.

［4］ 马伟，陈建国，张毛磊.基于尺度自适应和跟踪框自转的视频目标跟踪［J］.清华大学学报：自然科学版，2012，52（1）：92-95.

［5］ 张毛磊，陈涛，杨锐，等.基于稳像技术的飞艇监控视频目标追踪［J］.清华大学学报：自然科学版，2011，51（6）：809-813.

［6］ 邢文训，谢金星.现代优化计算方法［M］.北京：清华大学出版社，2005.

［7］董萍.基于蚁群算法求解TSP［J］.无锡职业技术学院学报，2008（5）：34-36.

［8］ 王果，戴冬.基于蚁群算法的TSP问题的求解［J］.河南机电高等专科学校学报，2008，5（9）：42-43.

［9］ 董萍.基于蚁群算法求解TSP［J］.无锡职业技术学院学报，2008（5）：34-36.

［10］马良，朱刚，宁爱兵等.蚁群优化算法［M］.北京：科学出版社，2008

［11］王玥，陶洪久.蚁群优化算法在TSP问题中的应用［J］.武汉理工大学学报，2006，11（11）：24-26

［12］Hao F，Daugman J.A fast search for a large fuzzy database［J］. IEEE Transacrionson Information Forensicsand Security，2008，2（3）：204-206.

［13］刘辉.最近邻居搜索的模糊实现［J］.上海电力学院学报，2011（2）：160-162.

［14］冯剑，岳琪.模拟退火算法求解TSP问题［J］.森林工程，2008（1）：94-96.

［15］康立山，谢云.非数值并行算法［M］.北京：科学出版社，1994：2-129

［16］穆艳玲.遗传算法在TSP问题中的应用［D］.天津：天津师范大学，2004.

Introduction of the Low-altitude Safety M onitoring Airship and Study on its Driving Route Problem

Li Yanwu，Su Guofeng and Yuan Hongyong
（Institute of Public Safety Research，Department of Engineering Physics，Tsinghua University，Beijing 100084，China）

In the earthquake disaster rescue，using Low-altitude Safety Monitoring Airship is an effective method to know more about the disaster situation.Due to the limitof signal transmission distance，how to design the driving route，considering the needs of disaster rescue and technical parameters of the airship，is a big problem needed to be resolved，and also an important part of airship command system.At first，we introduce advantages and functions of the low-altitude safetymonitoring airship.Then to solve the problem，considering the practical situation of disaster rescue，we transform the problem to the TSP problem and compare the effect of the ASA，NNS，SA and GA through simulation experiments.As the effectof ASA arithmetic is stable and takes less time，we finally decide to adopt the ASA algorithm as the core algorithm，and put forward the solutions to the driving route problem.

earthquake rescue；disaster monitoring；safety monitoring；airship；driving route；traveling salesman problem

X43；TP311

A

1000-811X（2015）04-0135-09

10.3969／j.issn.1000-811X.2015.04.026

李延武，苏国锋，袁宏永.低空安全监测飞艇介绍及其行驶路线问题研究［J］.灾害学，2015，30（4）：135-142.［Li Yanwu，Su Guofeng and Yuan Hongyong.Introduction of the Low-altitude Safety Monitoring Airship and Study on its driving route problem-Li Yanwu，Su Guofeng and Yuan Hongyong［J］.Journal of Catastrophology，2015，30（4）：135-142.］*

2015-04-21 修改日期：2015-06-08

国家“十二五”科技支撑项目（2015BAK10B00）

李延武（1988-），男，安徽安庆人，博士研究生，主要从事应急救灾管理方面的研究.

E-mail：liyw11＠mails.tsinghua.edu.cn