基于模糊神经网络的参数自整定PID控制器
2015-05-12郑晋平
郑晋平
(太原理工大学信息工程学院,山西太原030024)
本文是基于模糊神经网络而设计的PID控制系统,它有很强的自适应性,而且可以在控制中提取模糊规则,并达到其三个参数比例积分微分的自整定。它既有常用PID控制所含有的优点,如:原理规范简洁,实用方便等,同时在精度和灵活性等方面有更大的优势。这种控制系统就目前而言也是十分先进的控制系统。在本文中通过对RBF径向基神经网络的合理利用,以此为辨识器进而对控制系统中的被控对象进行了精准的建模,进而让整个PID的控制在很大程度上有了实质上的提高。
1 模糊神经参数自整定PID控制器模型
因为Mamdani模型与人们的表达及思维习惯相一致,并且易于专业知识的表达,所以依据文献[2]本文对控制系统设计时选用了此模型。PID控制器的模型如图1。
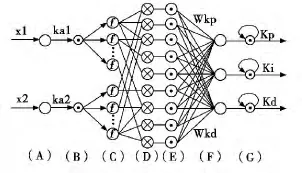
图1 模糊神经网络自适应PID控制器模型
1)模糊规则前件网络
假设X代表输入向量:X=[x1x2]并且x1代表偏差,其中论域的范围是 -3~3,x2的论域的范围是 -1.5~1.5。其中语言变量值,其中关于 xi第 j个变量值,论域上的模糊集合,分别代表了负的大中小与正的大中小和零。2;j=1,2,…,7)是其所对应的高斯函数。在上图1中的A层至E层代表规则前件部分,Kai代表A,B两层的连接权值,即量化因子,向量Ci为中心值、di是宽度。输入和输出之间的关系:
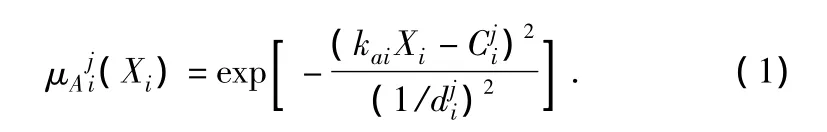
本文运用了模糊化方法,通过单点模糊集合,通过D层和输入量能够求出规则强度:
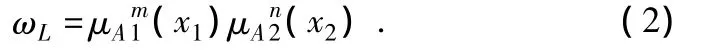
在上式中:m,n=1,2,…,7;L=1,2,…,49。
E层将值进行了取大。所以这49条控制规则的结果可得:

在经过取大运算之后,输出控制是所有规则中最强的一条。剩余的48条不进行当下时刻的控制。这种近似的处理既可以在很大程度上减少运算量,也不会影响控制的精度,提高收敛速度。
2)模糊规则后件网络
整个规则的后件部分是由网络F和G两层表示的。F层的目的是实现清晰化,阈值与调整权值是结论,能得出输出量。本文实现了收敛速度的提高,也通过G层的神经元接收延时输出信号攻克了多层网络的普遍收敛速度慢的不足。得到后件网络输出:

与3个连接权值对应的三个阈值,分别为Wbp、Wbi和Wbd。θ是值为0.8的递归系数。
PID控制器的增量:
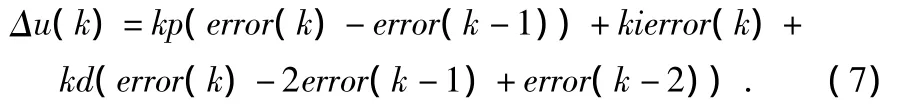
在控制系统中,PID参数自整定为使控制器的被控对象拥有良好的动态和静态性能,通过找出PID的三个可调参数Kp、Ki、Kd,找到与 e、ec之间关系,通过之后的不断监测和调整,达到其变化对控制参数的不同要求。
2 模糊神经PID控制器(自适应)的学习算法
在本文中所设计的网络控制器FNNC是模糊神经的网络控制器,它是一个多层的网络,通过文献[1]改变梯度下降来调整参数,不过仅仅调整k采样时刻被激活的函数中心值、宽度、阈值和连接权值,其余有关参数不变。它的优点是能通过误差反传的方法进行权值调整,十分有效的改变了权值调整的不确定性和盲目性;同时还可以快速调整相同分类模式的输入向量X所激活的参数,其余参数保持先前的调整结果,所有规则都与误差和其变化率有关,最终都会被激活。它们的相关参数都能够逐个被学习和优化。而具体到时刻所对应规则以及语言变量值函数的激活,对输入函数和规则强度取大就能得出。如果某一时刻输入的两个函数值相等,激活函数的语言值小。系统框图如图2。
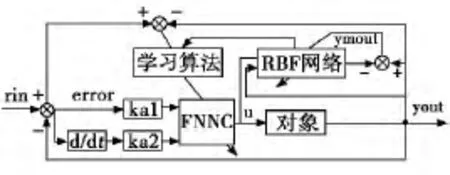
图2 模糊神经网络自适应PID控制系统框图
定义性能指标函数为:
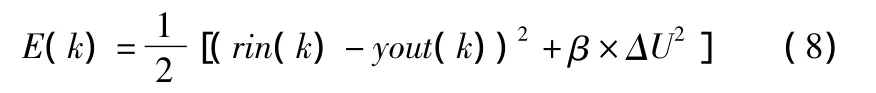
式中,增量ΔU,加权系数β。实际输出yout(k)。期望输出rin(k)。
可以根据梯度下降法来修正网络权系数,也就是按照E(k)对加权系数的负梯度方向进行搜索和调整,与此同时加上一个收敛惯性项。
设(G)层Kp、Ki和Kd的反传误差信号分别表示为δkp、δki和 δkd,则

式中x(1)=error(k)-error(k-1);x(2)=error(k);x(3)=error(k)-2error(k-1)+error(k-2)。
Wkp的迭代算法为:

式中,ηp是学习速率,0<ηp<1,αp为惯性系数,0<αp<1,能加快收敛

同理可得Wki和Wkd迭代算法,其中

对应的阈值Wbp迭代算法如下:(Wbi和Wbd的迭代算法略)
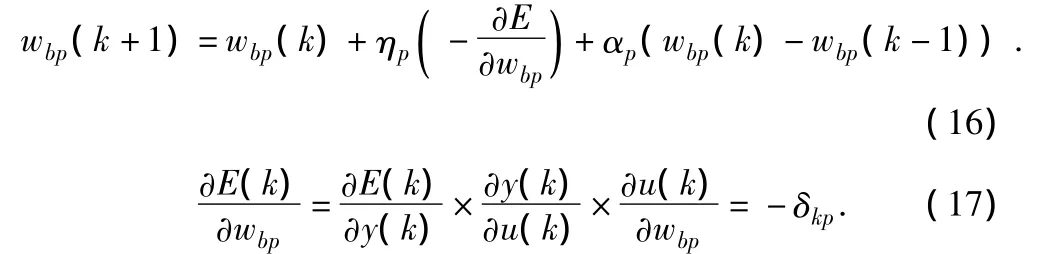
输入函数中心值和宽度:(误差变化ec语言变量值的隶属度函数和输入量化因子Kai的迭代算法略)
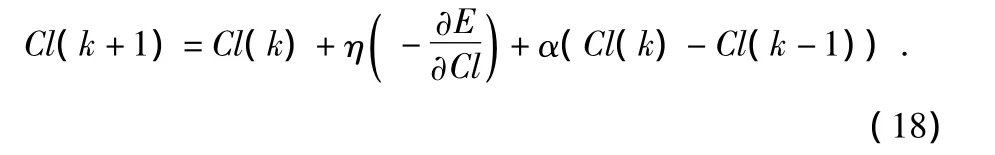
式中
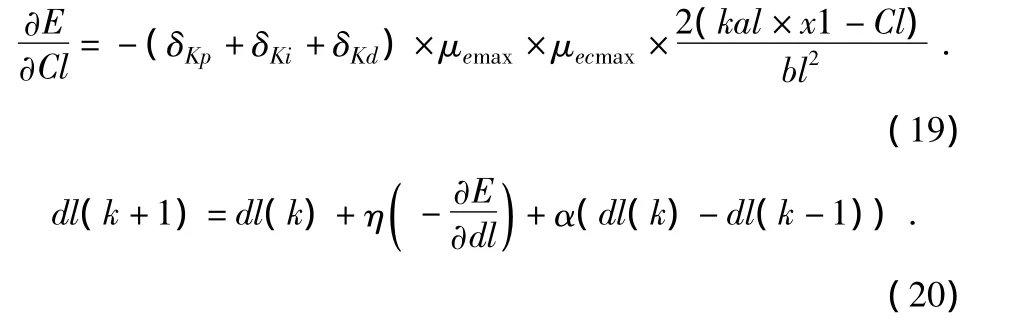
式中
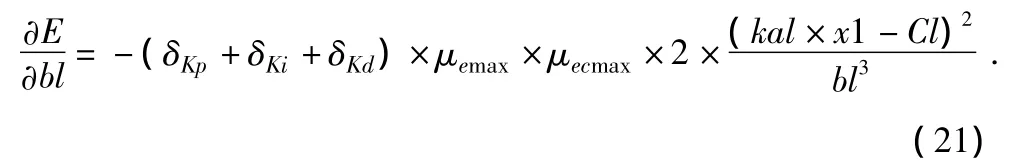
其中,μecmax和μemax代表误差和其变化的函数值。
3 模糊神经自适应PID控制器改进的学习算法
改进一:通过实践可以证实,e(k)、Δe(k)是影响PID学习修正的主要因素。所以可以改变模糊神经PID中的误差信号
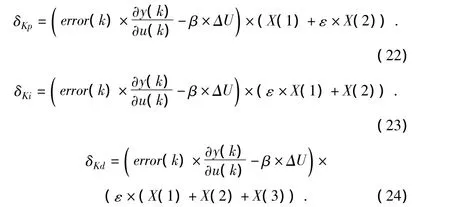
改进二:若想增大整个PID的平稳度,来加大对于复杂的被控对象时的适应能力,可以对系统的误差信号进行改进:

其中ε和λ为修正系数,0<λ<1;0<ε<1。
4 RBF神经网络辨识器结构与学习算法
RBF是局部逼近网络,它的径向基神经网络是两层前馈网络且含单隐含层。本文所设计的RBF神经网络结构选3-8-1,其中输入层节点仅仅将输入信号传递到隐含层,在隐含层与输出层,分别使用高斯与线性函数。它的三个输入信号是被控对象的输入、输出信号的历史信息u(k-1)、yout(k-1)以及yout(k-2);ym(k):输出信号。
辨识器的性能指标函数为

调整和优化输出层权值可以参照梯度下降法,梯度下降法也可以调整隐含层节点宽度及节点中心。
在被控对象经由辨识器进行建模后,可以根据网络结构,从输出信号ym(k)到输入信号u(k-1)计算得到k时刻的,也就是近似得到,把值提供给PID控制器,进而达到提高控制精度的目的。
5 学习速率和惯性系数等的获取
本文摒弃了人进行手工试凑待定加权系数这种费时费力的方法,而是利用遗传算法进行了优化:
1)初始群体的生成:可以随机生成种群并以实数编码,然后将种群的规模大小设定为40,在整个系统中有FNNC、辨识器惯性系数等13个参数需要优化。可以将参数作为分量构成编码。参数都为正小数。
2)适应度计算:参数选取的指标:
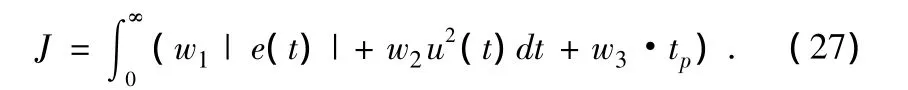
式中:u(t)控制器输出,e(t)为系统误差,tp为上升时间,w1,w2,w3代表权值。
3)复制、交叉和变异:线性复制,其适应度随复制机会成正比变化。随机交叉和均匀变异。
被控对象:气泡水位,迭代后结果:β=0.71,λ =0.02,ε =0.12,ηp=0.77,αp=0.86,ηi=0.19,αi=0.05,ηd=0.67,αd=0.75,η =0.59,α =0.45,ηf=0.1,αf=0.1。(ηf,αf为辨识器的学习速率和惯性系数)
6 仿真
用某锅炉的汽包水位当做被控对象,则其蒸汽对于水位的传递函数可以表达为如下公式:
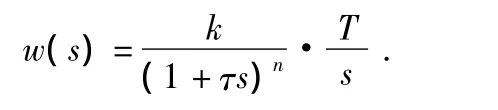
式中 k=2.613,T=0.747,n=2,τ=6.7。
控制选择1 ms的采样时间,并且对整个控制系统进行方波响应的仿真实验。其结果如图3、图4所示。

图3 模糊神经PID控制系统方波响应曲线

图4 PID参数自整定曲线
7 结论
通过仿真实验可以得到:基于模糊神经网络的PID控制系统对环境的变化有着很强的自适应能力。并且能够获得函数和控制规则,时变系统有很强的适应性。
[1]Martin T,Hagan,Howard B,et al.神经网络设计[M].戴葵,译.北京:机械工业出版社,2004.
[2]易继锴,侯媛彬.智能控制技术[M].北京:北京工业大学出版社,1999.
[3]徐春梅,尔联洁,刘金琨.动态模糊神经网络及其快速自调整学习算法[J].控制与决策,2005(2):226-229.
[4]沈晓蓉,范耀祖,李敬.基于递归模糊神经网络的鲁棒BP算法研究[J].航天控制,2004(3):26-30.
[5]程启明,陈刚,王勇浩.一种模糊神经网络控制系统研究[J].系统工程与电子技术,2005(3):501-504.
