基于空间信息的核模糊C均值聚类图像分割

沈 灏

(中北大学电子测试技术国家重点实验室，山西太原030051)

近年来，模糊分割算法由于比硬聚类分割算法能保留更多的原始图像信息，受到人们的极大关注，特别是模糊C-均值聚类算法(FCM)作为一种无监督聚类算法，在图像分割领域得到广泛应用［1，2］。

传统的FCM算法虽然快速简单，但并没有考虑目标物体的形状等先验知识，没有对样本特征进行优化，而是基于样本特征间的欧氏距离进行聚类。对噪声和异常点缺乏足够的鲁棒性，分割时间依赖于图像的大小，因此图像越大，分割时间越长。在过去几十年中，随着对模糊C-均值聚类算法的深入研究，针对其不足，国内外学者提出了许多改进的FCM算法，并融合其他技术以提高图像分割性能。Ahmed等［2］结合空间邻域信息，提出FCM_S算法，取得了好的分割效果;陈和张等［3］人又在此基础上提出了其变体算法FCM_S1和FCM_S2，减少了运算量。Wang X等［4］提出运用权重思想确定像素点隶属度，抑制了噪声的干扰。结合空间信息的FCM增强算法已有效地用于图像降噪及图像分割［5］。后来很多学者提出了基于核函数的模糊C-均值聚类算法(KFCM)，通过引入核函数将传统的FCM推广到了核空间，对图像的特征具有较好的适应性，同时核函数对噪声具有很好的抑制能力。因此，学者们在FCM算法中引入核函数。Zhang和Chen等用非线性函数对图像像素进行空间变换，将FCM_S算法、FCM_S1算法和FCM_S2算法扩展到相应的核版本，以此来增强FCM_S算法、FCM_S1算法和FCM_S2算法的抗噪性能，在新的特征空间按照FCM算法对图像各点进行聚类。

本文结合空间邻域和灰度信息，引入核函数，针对RFCM［6］算法未考虑噪声和邻域之间关系，无法有效避免噪声影响的缺点，提出基于空间信息的核均值聚类分割算法。实验表明，提出算法分割结果保留了图像更多细节和边缘信息，同时具有较强的抗噪声能力。

1 RFCM算法

FCM算法最早由 Dunn提出，而后由 Bezdek［1］进行完善。传统的FCM算法是一种迭代算法，将图像中所有的像素点当作孤立的数据进行聚类，是一种无监督分类方法。由于原始的FCM算法未考虑图像的空间信息，这使得算法在运行过程中对噪声十分敏感。FCM算法通过将图像I={f(i，j)，0≤i≤M，0≤j≤N}分成 c类，实现图像的分割，其中f(i，j)为特征数据。

RFCM算法是广义模糊C均值聚类算法的改进算法［11］是FCM的一个改进算法。通过在隶属度函数中引入一个单一数据点的量，使得分配更清晰。

RFCM的目标函数如下:

使用拉格朗日数乘法最小化式(1)，新的聚类中心vi和隶属度函数uij更新方程如下:

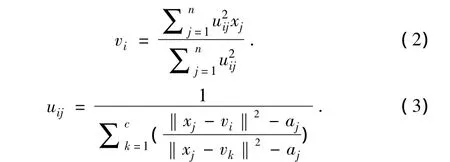
为满足 uij，0≤uij≤1，α(0≤α≤1)，aj= α·min{‖xj－ vs‖2|s∈{1，2，…，c}}参数控制收敛速度，当 α =0 时，RFCM 算法等价于FCM。

在参数α选取适当的情况下，RFCM不仅可以更快速地聚类，还具有良好的聚类性能。但是，RFCM算法中噪声被视为正常图像的一部分，未考虑噪声和邻域之间的关系，故无法有效避免噪声的影响。

2 改进的基于空间信息的核聚类算法

2.1 核表示和核函数

文献［3］提出了基于核函数的FCM算法KFCM。Φ:x∈X⊆Rd|→Φ(x)∈RH(d＜＜H)是由一个非线性映射到一个高维特征空间F的变换，在F中，欧氏距离‖x－y‖2被‖Φ(x)－Φ(y)‖2取代，定义为:

每一个线性算法仅利用内积就可以很容易地扩展到非线性，只要通过满足Mercer条件的核函数［15］。因为高斯核函数对应的特征空间是无穷维的，有限的样本在该特征空间肯定是线性可分的，所以较常用。本文中采用高斯核函数。这里，核函数K(x，y)被用来计算F的内积。定义核函数如下:

将式(4)带入(5)式得到:

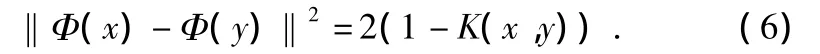
样本方差来估计σ2被定义为:

2.2 KSNRFCM 算法

本算法引入核函数并提出结合局部空间和灰度信息的一个新的模糊C均值聚类图像分割算法(KSNRFCM)。通过内核替代(即方程(6))，所述核广义模糊C-均值聚类目标函数如下:

利用拉格朗日乘子法得到隶属度函数和聚类中心:

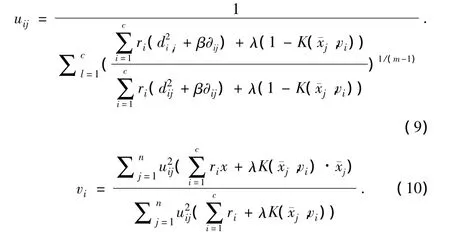
NKRFCM算法的基本步骤如下:

步骤1:确定聚类数c，模糊加权指数(此处直接定义为2)，迭代停止阈值ε，令初始迭代次数为n=0。

步骤2:初始聚类中心v(0)i。

步骤3:根据式(9)计算新的隶属度uij。

步骤4:根据式(10)计算新的聚类中心vi。

步骤5:停止条件|Unew－Uold|＜ε，算法终止，否则，令n=n+1，转至步骤 3。(U=［u1，u2，…，uc］是聚类原型向量)

步骤6:按照最大隶属度原则对图像进行分割。

3 实验结果与讨论

为验证本文算法有效性，实验中将算法用于lena图像进行分割实验，并与FCM、RFCM、NRFCM以及KGFCM分割方法进行了比较。为验证算法可行性，在Visual C++6.0环境下进行实验，在实验中选取λ=0.02。所有算法在Microsoft windows XP计算机上进行。

3.1 含噪图像实验结果分析

为验证试验结果有效性，对图1(a)原始图像加入高斯噪声和椒盐噪声，分别运用RFCM、NRFCM算法与本文所提出算法进行比较，设置分类数c=2。

图1 加入0.5的高斯噪声后经不同算法分割后的结果对比

图1(b)为加入均值为0，局部方差为0.01的高斯噪声后的图像，图1(c)为RFCM算法分割结果，图1(e)为NRFCM算法分割结果，图1(f)为本文算法分割结果。

可以看出，利用本文所提出算法进行图像分割，噪声抑制效果比RFCM算法和NRFCM算法更好。分割后，方形零件周界清晰。

3.2 图像分割细节实验结果分析

将本文算法应用于lena图像进行分割实验，并与FCM、RFCM、NRFCM以及KGFCM分割方法进行了比较。

图2 lena图经不同算法分割后的结果对比

图3 本文算法对比描述

如图2，(b)是FCM算法分割结果;(c)为KGFCM算法分割结果;(d)为RFCM算法分割结果;(e)是NRFCM算法分割结果;(f)本文提出算法分割结果。

对比图2，结合图3本文算法分割lena图对比明显区域描述看出:对于图中的脸部、嘴巴和帽子流苏部分的细节与边缘部分(红框区域)，本文所提算法分割效果更好，细节显示更充分。结合图像的分割性能指标(表1)，本文所提出算法在分割过程中保留了更多图像的细节信息。

3.3 分割性能指标分析

为了对算法进行客观、定量的评价，本文采用常用的图像分割评价标准最大香农熵Hmax［6］对上述分割结果进行评价，定义如下:

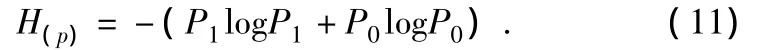
其中，P0，P1分别表示分割图像的二值输出为1和0的概率。对大多数图像而言，香农熵代表图像的信息量，如果分割后的图像香农熵越大，分割图像从原始图像中得到的信息量越大。分割图像细节越丰富，总体分割效果越好。这里分别对lena图像、flower图像以及脑出血放射图像进行仿真验证。

得到分割性能指标如下表所示:

表1 分割性能指标

4 结束语

本文提出结合空间邻域和灰度信息的新的模糊C-均值聚类图像分割算法(SNRFCM)，然后在新的目标函数中采用内核感应距离代替欧氏距离，同时通过引入核函数，提出了一种基于空间信息的核聚类图像分割算法(SKNRFCM)。通过使用一个惩罚因子，有效地减少噪声对聚类结果的负面影响。通过使用聚类权重，有效避免部分噪声影响。实验结果表明，通过与 FCM、RFCM、NRFCM和KGFCM算法进行比较，本文所提出算法具有良好的分割性能，尤其在图像分割细节和边缘方面，同时具有较好的抗噪声能力。

［1］BEZDEK JC.Cluster Validity with Fuzzy Sets［J］.Cybernetics and Systems，1974，3(3):56 －75.

［2］AHMED MN，YAMANY SM，MOHAMED N，et al.A Modified Fuzzy C-means Algorithm for Bias Field Estimation and Segmentation of MRI data［J］.IEEE Trans Med Imag，2002，21:193 －199.

［3］Zhang DQ，Chen SC.A Novel Kernelized Fuzzy C-Means Algorithm with Application in Medical Image［J］.ArtificialIntelligence in Medicine，2004，32(1).

［4］Wang X，Wang Y，Wang L.Improving fuzzy c-means clustering based on feature-weight learning［J］.Pattern Recognition Letters，2004，25:1123 －1132.

［5］WU M，SCHOLKOPF B.A local learning approach for clustering［J］.Adv.Neural Inf.Process Syst，2007，19:1529－1536.

［6］马义德，齐春亮.基于遗传算法的脉冲耦合神经网络自动系统的研究［J］.系统仿真学报，2005，18(3):722－772.