强磁性体ΔT异常计算的误差分析研究
2015-05-12袁晓雨姚长利郑元满李泽林王君恒
袁晓雨, 姚长利, 郑元满, 李泽林, 王君恒
地下信息探测技术与仪器教育部重点实验室和地质过程与矿产资源国家重点实验室,中国地质大学(北京), 北京 100083
强磁性体ΔT异常计算的误差分析研究
袁晓雨, 姚长利*, 郑元满, 李泽林, 王君恒
地下信息探测技术与仪器教育部重点实验室和地质过程与矿产资源国家重点实验室,中国地质大学(北京), 北京 100083
本文主要针对当前磁法勘探中高精度处理解释的需求,对强磁性体ΔT异常计算存在的误差进行分析研究.我们首先通过理论模型计算试验,证明常规计算采用的投影关系的ΔT与实际测量的模量差ΔT之间的误差E在磁异常幅值大时是明显存在的,其影响不容忽视.其次,当磁性强且剩磁存在时,投影ΔT曲线及其误差曲线在磁化方向与地磁场方向改变时具有一定的对称性;地磁场T0、磁性体形态(如二度水平圆柱体模型的半径r、柱体埋深R)和磁性参数(如磁化率κ)等参数确定的情况下,最大误差值出现在磁性体正上方,且其大小与磁性参数(κ)和模型体规模(如r/R)之间皆是指数关系;另外,研究还发现ΔT的计算误差曲线的一些其他规律特点,如在各纬度带上,ΔT计算误差的最大值Emax曲线的极值主要分布在中纬度地区;磁异常矢量Ta与地磁场T0的夹角θ逐渐变化时,随θ变化Emax曲线的极值分布在θ=90°~120°范围内;当磁异常幅值小于10000 nT时,最大误差近似为磁异常矢量垂直于地磁场方向的测点附近的误差值;另外,磁性体(圆柱体为例)的半径(即尺度)与埋深的比值r/R超过0.5,且磁化率超过0.1SI时误差已达到3.9 nT,磁化率增大与对应的Emax的值呈指数增长特点.因此,我们的研究表明,在强磁性体、磁异常幅值大的数据处理、反演及解释时,现有方法会产生较大的误差,应该基于严格的模量差ΔT,完善相应的处理以及反演方法.
总场异常ΔT; ΔT计算误差; 磁异常模量Ta; 剩磁; 磁化率
1 引言
磁法是矿产资源勘探的重要手段,是寻找一些金属矿类的主要方法之一.当今的高精度磁力仪如质子磁力仪、光泵磁力仪等,其灵敏度已分别达到0.01 nT和0.001 nT,因此,相应的高精度处理转换以及反演解释逐步受到重视,例如,强磁性体的剩磁影响和退磁效应近年来就受到普遍关注,相应的研究得到不断深化(Guo et al., 2001; Krahenbuhl and Li, 2007; Li et al., 2010),从而提高了处理解释的质量.
我们关注的是一个更加基础的问题,即ΔT异常近似计算的误差问题.因为在实际的情况中,当磁异常较弱时,这个误差通常非常小,所以在定性分析为主时这个问题一直被忽视,但当磁性体磁性较强时,所产生的磁异常幅值比较大,对后续定量计算和分析推断可能会造成比较大的影响.所以,在当今高精度勘探及处理解释越来越受到重视的新阶段,有必要对其影响进行重新评估和深入分析,以期设法避免不必要的误差,形成相应的更高精度的处理解释方法.
现在勘探所用的主力仪器——质子磁力仪(及光泵磁力仪)等直接测量地磁场总强度矢量T的幅值大小,将其与地磁场正常场T0的幅值相减以消除背景的影响,所获得的模量之差称为总场磁异常ΔT,基于研究的需要,这里我们称其为模量差ΔT,简称ΔT模量差.显然,它是由地下磁性体产生的磁异常矢量Ta引起的,与其大小和方向变化密切相关.航空磁测中Ta一般在几个nT到几千nT之间,一般不超过5000 nT(Blakely,1996;管志宁,2005),这时T0远大于Ta,ΔT就近似相当于磁异常矢量Ta在地磁场T0方向上的投影分量.这样,ΔT就和垂直分量异常Za以及水平分量异常Hax、Hay具有一样的物理意义,都相当于是磁异常矢量Ta的一个投影分量,我们称其为投影分量ΔT,简称ΔT投影.其重要意义是:由于其相当于分量了,则磁异常ΔT投影与磁性体磁化强度变成简单的线性关系,与地磁场T0无直接关系,后续的分量互换等计算将变得可行,并且正演及反演计算也将得到大大简化.而采用严格的ΔT模量差磁异常形式,上述优势则不存在,即地磁场T0在计算表达式中显式出现,现有的分量互换方法将变得不可行.而实测磁异常由于其复杂性,其分析解释离不开必要的定量计算分析,故处理转换计算以及正演和反演计算逐步成为很重要的中间环节.为此,当强磁性体产生了大幅值磁异常时,准确的ΔT模量差与看作投影分量的ΔT投影之间的误差到底有多大,对后续的处理以及反演会带来多大的误差和影响,正是本文关注和研究的内容.
2 总场异常ΔT计算误差原理
图1a是ΔT及其他相关物理量关系的示意图.图中O点代表测量点(例如图1b中的任一测点D点),该测点上地磁场正常场矢量为T0,地下的磁性体在该测点产生的磁异常矢量为Ta,测点O点处总磁场为这两者的矢量合成量T,质子磁力仪等磁场模量测量仪器所测量的是T的大小即模量.显然,如果没有磁性体产生的磁异常Ta的影响,磁力仪测量的将只是背景地磁场T0的大小.所以,通常将实测磁场值减去背景地磁场,获得的是由磁性体引起的剩余磁场,称为磁异常.磁力仪测得的地磁场模量T减去背景地磁场T0,所得磁异常称为总场异常ΔT.图1b为示意显示的地下一磁性体在斜磁化时产生的感应磁场即磁异常Ta的空间分布情况,图中的磁力线的分布直观地表现了Ta的空间形态和方向变化,以及在地表其磁异常的矢量表达.图中A、B、C、D、E等为地面不同测点,M为磁性体的磁化强度矢量,在地面不同测点处产生不同的磁异常矢量(红色矢量线),与地磁场矢量T0合成,将作用于磁测仪器,产生观测磁场.
图1a所示的任意观测点O处,地磁场总强度T、正常场T0,以及磁异常矢量Ta三者之间具有以下关系式:
T=T0+Ta,
(1)
ΔT是T与T0的模量差,我们记作ΔT模量差,即
ΔT模量差=|T|-|T0|=T-T0.
(2)
显然,这里的ΔT模量差主要取决于Ta,但ΔT模量差并不等于模量Ta.基于(2)式及图1a所示关系,可知
ΔT模量差≤Ta.
(3)
另外前人的分析已指出,航空磁测中Ta一般不超过5000 nT(Blackely,1996;管志宁,2005),这时,ΔT就近似为Ta在T0方向的投影,记作ΔT投影,即
ΔT模量差≈Tacosθ=Tacos(Ta,T0)=ΔT投影.
(4)
结合图1a及表达式(2)和(4)可以发现,ΔT模量差和ΔT投影都主要由Ta控制,但又都与T0密切有关.其中,ΔT模量差受T0的大小和方向双重影响,而ΔT投影只受T0的方向影响(在该方向上的投影),与其大小无关,这是两者的关键区别.
磁性体产生的磁异常Ta可以分解成三个分量Za、Hax和Hay,在正演计算中,通常也是通过先计算这三个分量,然后再将其合成获得磁异常Ta的.现在,ΔT也是Ta的一个投影分量,将其看成是投影的一个重要优点是,ΔT与Za等分量一样,与磁性体磁性(如磁化强度)之间就是简单的线性关系,而与地磁场大小T0无关,后续的磁异常处理转换及正反演计算都能得到大大简化.例如,磁异常三分量之间可以互换,ΔT作为分量,也将同样具有与三分量互换计算的理论基础;正演和反演中,如果只是磁性发生变化,也将是个线性问题.正因为如此,长期以来对于测量所得的ΔT模量差都直接将其当作投影分量ΔT投影.另外,至今所有文献中的处理转换和正反演计算中,ΔT都是当成ΔT投影对待的.
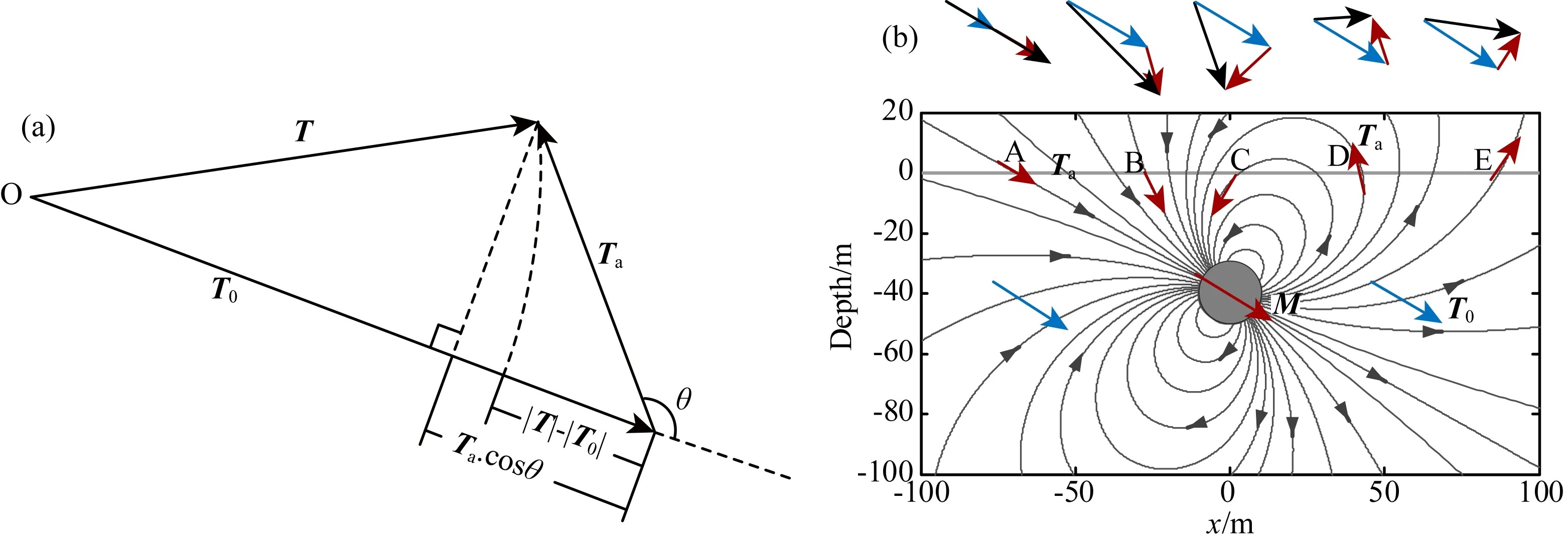
图1 地磁场及磁异常关系图
显然,基于图1所示原理图不难发现,由于地磁场T0的范围约为30000~60000 nT,如果Ta很大,即如实际的磁铁矿类等勘探中会遇到的数千纳特(例如:俄罗斯的库尔斯克铁矿磁异常超过100000 nT,已远大于地磁场大小)的磁异常,那么上述简化将引起明显的误差.这个误差还和哪些因素直接相关?具有哪些特点?下面我们将通过必要的分析和模型实验,加以研究评价.
由图1所示关系容易得到,实测值ΔT模量差与ΔT投影即计算值之间存在的误差E为
E=ΔT模量差-ΔT投影,
(5)
根据矢量三角形余弦定理,可得

(6)


(7)
结合前面(3)式可知
ΔT模量差≥ΔT投影.
(8)
另外,分析误差关系式(7)不难发现,磁性体产生的磁异常幅值Ta大(甚至与背景地磁场T0在数量级上接近),误差就会相当大.外在因素对ΔT模量差的影响是比较复杂的,因为磁性体分布有限,其Ta的大小和方向在测线剖面上变化明显(见图1b),所以T(=Ta+T0)随其相应变化,这样,ΔT模量差的影响会使误差E随测点变化而变化.当Ta的值一定,ΔT模量差越小(此时T与T0的值接近),误差就会变大.
为方便后面的定量对比分析,我们将ΔT模量差看作为实测数据,ΔT投影看作计算数据(至今都是这么对待的),并且将计算数据相对于实测数据的均方误差值与实测数据本身的标准差的比值定义为计算数据相对于实测数据的相对误差,这也是ΔT投影相对于ΔT模量差的相对误差.
3 强磁性体总场异常ΔT投影计算误差定量分析
关于岩石磁性的研究,前人进行过系统的岩石物理分析(Clark,1983;ClarkandEmerson,1991).其中,富含铁的带状建造及含磁铁矿的矽卡岩,其磁化率常见值可达2.0SI,最大可达4.0SI(ClarkandEmerson, 1991),而块状粗粒的(钛)磁铁矿和磁赤铁矿的磁化率还要更高,其常见值在1.0SI到6.0SI之间, 此特征在国内的强磁性铁矿区都有体现(方华竹,1978; 朱永刚等,2006;张恒磊等,2011;朱朝吉等,2011;ZhangandHu,2012);此外,变质岩中的条带状含铁构造的磁化率一般在0.01SI到3.0SI之间.我们的模型试验中磁性上限可据此确定.为简化问题,这里我们采用最简单的均匀磁化的二度水平圆柱体模型,分析ΔT的计算误差的变化规律.
由磁性体正演理论可知,磁性体产生的磁异常,其幅值主要受磁性体的规模、埋深,以及其磁化强度大小决定,而磁异常的变化特征(如剖面和平面分布特征)不仅与磁性体的几何形态有关,受磁化方向影响更大.为简单起见,我们首先选择了最简单的垂直磁化条件进行计算实验.取观测剖面长度为200 m,测点间隔为1 m,圆柱体半径为30 m,其中心埋深为40 m.地磁场强度设为50000 nT,磁倾角即为90°.这里地磁场为垂直向下,表明总场异常ΔT投影相当于是垂直分量Za.为使ΔT计算误差对比效果更加显著,我们设模型的磁化率为3.0 SI,即圆柱体模型具有强磁性.通常强磁性体不仅具有较强的感应磁化强度(感磁),而且具有较强的剩余磁化强度(剩磁),由于磁化方向为感磁与剩磁的合成矢量的方向,如果与地磁场方向一致,即可看成无剩磁或剩磁方向与感磁方向一致;反之,如果磁化方向与地磁场方向不一致,则表明有剩磁的影响,且剩磁方向肯定与地磁场方向不同,从而改变了合成的磁化强度方向.但为简化分析过程,这里的磁化率可看成是产生总的磁化强度的等效磁化率,这只是便于分析而假设的,不影响结果和分析.该圆柱体模型的ΔT计算结果见图2a所示.
计算中所采取的方法是先计算二度圆柱体在剖面上各测点处的磁异常垂直分量Za和水平分量Ha,其合成得到总磁异常矢量Ta和其大小,即模量Ta,再由Ta与T0合成即得总的磁场矢量T,进一步基于(2)式和(4)式即可得到ΔT的两种计算结果:
准确的ΔT模量差和近似的ΔT投影.由图2a可以看出:水平圆柱体的磁异常模量Ta对称,极大值位置对应柱体的中心点,异常幅值已达42000 nT,接近地磁场大小了,属于强磁异常.其次,ΔT模量差和ΔT投影在形态上一致,但显然在数值上已出现明显的误差,从误差值E曲线可以看出,在垂直磁化条件下,误差最大值不在异常最大值处(异常最大值处误差为0),而是在异常极值两侧,误差值已达5000 nT,达到异常幅值的18.5%,显然这已经完全不能忽略了,会直接影响后续的定量评价.实际上基于理论公式可知,对于地磁场方向和磁化方向都垂直向下条件下的水平圆柱体,其磁异常ΔT投影与垂直分量Za完全一样,其表达式由任意磁化的(9)式(Blakely,1996;管志宁,2005;李才明和李军,2013)
ΔT投影=
(9)转化为

(10)
而ΔT模量差的值是地磁场总强度T与地磁场T0的模量差值,由(2)式和(9)式可得具体表达式如下:

-T0,
(11)其中,R为圆柱体的中心埋深,μ0为真空中的磁导率,ms为单位长度的磁矩,I0和I分别为地磁场倾角和磁化强度倾角.显然,由式(10)可得到ΔT投影的两个0值点的距离正好是圆柱体埋深的2倍,与由图2a的ΔT投影曲线得到0值点的距离为80m完全一致,这就是简单反演方法中的特征点法.但是,从实测角度来看,对该模型实测的将是严格的ΔT模量差,而不是近似的ΔT投影,如果仍然取图2a中ΔT模量差曲线的0值点的距离(该距离值约为98m),应用式(10)推测的圆柱体中心埋深则为49m,与实际深度40m相比,误差将达23%.显然,此时再将ΔT模量差当作近似的ΔT投影对待,在定量计算时会造成明显的误差,这是强磁异常定量计算及分析时需要注意的方面.
我们再补充一个反向磁化实验,具体为保持地磁场不变,磁化强度方向改为反向,即磁化方向向上,与之对应的ΔT投影和ΔT模量差曲线对比如图2b所示.可以看出,对称反向磁化后,两次ΔT投影曲线变为正负镜像关系,是严格对称的,对称轴为0值线,但ΔT模量差曲线则不存在严格对称性这样的特征,表现为只是正负镜像,形态不严格对称,镜像轴抬高离开0值线.还可以看出,ΔT模量差在负值区比ΔT投影曲线“瘦”,在正值区比ΔT投影曲线“胖”,这是因为始终存在ΔT模量差≥ΔT投影,即E总是大于等于0的缘故.
由于ΔT模量差≥ΔT投影,如果我们在实际情况中将ΔT投影当做ΔT模量差进行后续的定量计算,如反演,其反演结果所对应的场值和规模会偏大,这是不容忽视的,后面的模型计算实验也证明了这点.
上述分析的例子中,如果磁化方向与地磁场方向不一致,则表明肯定有剩磁的影响.保持上述其他条件及参数不变,只改变磁化方向及地磁场方向,对圆柱体模型算例进行进一步分析,则该水平圆柱体的磁异常各参量沿剖面将发生变化.
图3是磁化方向和地磁场方向都在变化的几个算例,概括地展示了磁异常的变化特征.由图3可见,虽然磁异常矢量Ta与磁化方向密切有关,但其大小即模量Ta不受磁化方向的影响,这是二度体磁异常的特征,理论上已证明这点(Kontis and Young,1964).但对三度体而言,则不具有该特征,三度体的磁异常模量受磁化方向影响,只是与磁异常分量(ΔT投影、Za、Hax和Hay),相比较小,前人对此已作大量分析,这里也不再赘述.
从式(9) 和式(10)可以看出,ΔT投影和ΔT模量差与磁化倾角I与地磁场倾角I0的和有关,为简化起见,我们设S=I+I0.结合式(9)、(10)可以得出,当S为定值时,二度水平圆柱体模型在剖面上的ΔT投影曲线、ΔT模量差曲线以及误差E的曲线都完全一致,如图3(a、e、i)、图3(b、f)或图3(d、h);以上三条曲线在S和360°-S情况下是关于y轴对称的;由于ΔT模量差≥ΔT模影,所以S和180°-S情况下ΔT投影曲线关于原点对称,但是ΔT模量差曲线却不具备这个对称性的特点,相应的误差E的曲线也不再具有对称性;同理,S和180°+S情况下ΔT投影曲线关于原点对称,但是ΔT模量差与其相对应的误差E曲线不再具有对称性.
S=0°时,可有多种组合方式,如:磁化倾角I=0°,地磁场倾角I0=0°,即均为水平方向,如图3c所示;或如:I=-90°,I0=90°,结果如前面图2b中的磁化方向向上的状态,误差E曲线关于y轴对称分布,其极大值为11000 nT,剖面相对误差为38.6%,误差明显.
当S=180°时,也有多种组合方式,如:I=90°,I0=90°,结果如图3g所示;或I=0°,I0=180°,误差E曲线关于y轴对称分布,其误差的极大值在所有情况里面是最小的,为5673.3 nT,剖面相对误差为18.8%.

图2 (a) 水平圆柱体磁异常各参量剖面(地磁场及磁化方向均垂直向下); (b) 地磁场T0垂直向下且磁化方向分别为向下和向上时的水平圆柱体模型的ΔT的模量差曲线与投影曲线对比

图3 二度水平圆柱体的ΔT异常及其误差曲线
当S=90°以及S=270°时,如图3(a、e、i)所示,ΔT投影曲线本身关于原点对称,此时误差E是一条单峰曲线,最大值达到16820 nT,是此处Ta(41770 nT)的40.3%,剖面相对误差为33.93%,影响显然较大.另外注意,此时误差最大值点位置并不在模型体中心点正上方,而是稍有偏移.
通过上面的分析可知,S(=I+I0)一定时,圆柱体对应的ΔT投影、ΔT模量差以及误差E曲线都是相同的,所以我们这里来探讨在当前磁参数下S在0°~360°范围时剖面上误差E的最大值随S的变化规律,结果如图4所示.可以看出,曲线关于S=180°对称,在S=180°处出现一个极小值,且曲线的极大值出现在S=65°附近,为17798 nT,是此时异常幅值Ta(42187 nT)的42.2%.该最大误差值位于模型体中心点正上方位置,此时整个剖面的相对误差为37.3%.

图4 ΔT误差最大值Emax随S在0°~360°范围内的变化
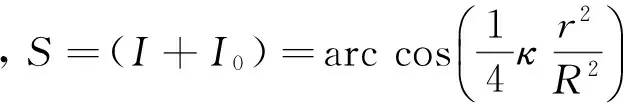
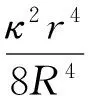
(12)
此时ΔT模量差=0.
从式(12)可以看出,误差最大值与T0之间是线性关系,与κ和r/R之间皆是指数关系,可见磁化率κ对误差值的影响呈指数递增,一旦磁性体的磁化率较大,它造成的误差影响我们更加不能忽视.
4 ΔT计算误差的几个特点规律分析
4.1 地表随纬度变化ΔT计算误差的特点
在地球表面,不同的纬度对应的磁倾角、磁偏角、总场大小等磁参数都不相同,所以,各个点上的ΔT的计算误差E值也随着这些磁参数的变化而改变.通过对东经120°、纬度-90°~90°进行一系列地磁参数的换算,得到各纬度所对应的磁倾角、磁偏角、总场等数值.为评价地表各纬度带上误差E的变化情况,我们假设每个纬度取一个剖面进行误差E的计算,然后,分析每个剖面上E的最大值分布.继续用之前的二度水平圆柱体模型,为观察对比,等效磁化率分别取0.1 SI、1.0 SI 和3.0 SI.
在东经120° 经线上,地理纬度-90°~90°对应的磁倾角范围为-85°~89°,地磁场总强度大小的变化范围为39954~65960 nT.误差E的最大值随磁倾角变化的规律如图5a所示,可以看出,曲线关于磁倾角0°是对称关系,曲线在磁赤道和磁两极处总是处于一个极小值的状态;并且不管磁化率κ如何变化,曲线极大值总是出现在中纬度范围,整个曲线的幅值随磁化率κ的增加而增加.可以看出,磁化率κ=0.1 SI时,ΔT误差最大值曲线和相对误差曲线幅值都很小,在图中近似一条直线,可以忽略.磁化率κ=1.0 SI时,曲线在I=±50°处达到2000 nT的极值,是此时磁异常Ta的14.3%,且从图5b中可以看到此时相对误差整体在7%以上,最大值达到13.0%;随磁化率增长到κ=3.0 SI时,误差最大值曲线整体大于6000 nT,最大值达到16000 nT,是此时磁异常Ta的38.6%,而相对误差也整体处于15%~40%之间,可见已不能忽略.所以,如果以ΔT的计算误差和相对误差5.0%为误差衡量的一个标准,那么磁化率超过1.0 SI时我们通常就要开始重视ΔT计算误差了.
磁化率不同,对应的ΔT误差最大值曲线和相对误差曲线形态基本一致.磁化率越高,曲线幅值就越大,且集中在磁倾角±30°~±50°区域,对应的纬度带为-20°~-60°及20°~60°的中低纬度地区,这说明中低纬度地区不仅ΔT误差更大,相对误差也更大.
4.2T0、Ta与ΔT计算误差关系
假设在某测点上,地磁场T0与磁异常大小Ta均不变,但T0与Ta夹角θ发生改变时,两者关系可用图6a表示.显然,由公式(7)可知ΔT模量差=0时,误差为极大值:

(13)
此时,图6a中T0、T、Ta三者构成等腰三角形,Ta与T0的角度θ为:
(14)
从式(7)和图6b也可以看出,Ta变化对应的其曲线幅值并不是线性增长关系.我们设正常场强度取值为T0=50000 nT,磁异常Ta取值为Ta/T0=0.1,0.5及1.0,对应的误差E随二者夹角θ变化如图6b所示.可以看出,当θ角为0°、180°时,Ta与T0的方向在一条直线上,误差E的值为0,且误差曲线都关于θ=180°对称.
综上,Ta/T0在0~1范围时,Emax出现的位置范围是θ=90°~120°(和θ=240°~270°)之间,且Emax≤0.5Ta.
根据误差极值关系式(13),我们可以很容易得到一些指标性信息,见表1.例如,现在的质子磁力仪和光泵磁力仪的测量精度已分别达到0.01 nT和0.001 nT,则当测点上磁异常幅值达到Ta=10 nT即可引起0.001 nT的最大误差;高精度测量通常要求精度达到0.01 nT,则易得Ta=31.6 nT即可引起这样的误差;而100 nT的中等强度磁异常,可引起0.1 nT的误差;磁异常达到1000 nT的幅值时,引起的误差E极大值可达10 nT,以高精度处理解释的标准衡量,这个误差已经不能忽视了.过去认为磁异常小于5000 nT的幅值时,其误差可忽略(Blackely,1996;管志宁,2005),而此时引起的误差E极大值可达250 nT,这显然表明,在强磁异常及高精度勘探阶段,其误差及其影响是需要考虑的了.

表1 误差最大值Emax与磁异常Ta的相互对应关系

图5 东经120°各纬度带的ΔT误差分布

图6 (a) Ta与T0夹角θ在0°~360°范围内变化示意图; (b) Ta/T0=0.1/0.5/0.1时ΔT计算误差随二者夹角变化规律
另外,我们进一步比较分析Ta垂直于T0的特殊情况.此时ΔT投影≡0,所以ΔT的计算误差E=ΔT模量差,如图7a所示.由于此时Ta与T0方向不变,假设地磁场T0大小不变,分析此种情况下E随Ta大小变化的情况.则由图7a的图形关系,利用下式非常容易计算该误差:

(15)
例如,T0为50000 nT保持不变,Ta=5000 nT时,E⊥=249.39 nT,非常接近由式(13)确定的最大误差Emax=250 nT.当磁异常Ta=10000 nT时,E⊥=990.20 nT,也接近由式(13)确定的最大误差Emax=1000 nT,所以,可以认为,当磁异常幅值小于10000 nT时,最大误差为磁异常矢量垂直于地磁场方向的测点附近,这对于我们基于磁异常剖面定性判断最大误差区域是有帮助的.当Ta=50000 nT时,此时误差很大,为E⊥=20710.68 nT,而最大误差Emax=25000 nT,此时两者差异已很大,当然磁异常如此之大的情况,在实际勘探中几乎没有,所以,可以不考虑.
4.3 圆柱体ΔT误差最大值随r/R变化的特征

从图8中可以看出,磁化率在0.1SI时,Emax曲线走势平缓,r/R=0.5时,Emax=3.91 nT;r/R=0.8时,Emax=25.60 nT;r/R=1.0,即模型已出露地表时,最大值Emax是62.5nT,高精度勘探的处理解释中已不能忽略该误差了.磁化率为1.0SI时,r/R超过0.5之后,Emax曲线增长趋势明显,r/R=0.8时,Emax达到2560nT,这个误差已经非常大了.当磁化率达到3.0SI时,r/R超过0.3之后,Emax曲线增长趋势便非常明显.
综上分析可以看出,ΔT计算误差可能会对反演工作造成后续影响.用ΔT模量差的值来进行反演计算造成的误差是不可忽视的,或者说,采用严格的ΔT模量差值来进行反演,其计算公式需要重新确定,不能使用基于ΔT投影值的方法.由于篇幅原因其反演结果对比在这里不再展开论述.

图8 磁化率κ变化时,一条剖面上的误差最大值随r/R的变化关系

图7 Ta垂直T0时(a)ΔT计算误差示意图, (b)E⊥及Emax随Ta的变化曲线
5 结论
基于高精度勘探的需要,我们对强磁性体ΔT异常计算存在的误差进行了分析研究和评估,取得以下认识.
(1) ΔT异常存在的误差来源于用近似的ΔT投影代替实测的ΔT模量差.之所以选择ΔT投影,是因为其计算只与地磁场T0方向有关而与其大小无直接关系,因而ΔT投影与地磁场T0之间是良好的线性关系,且便于正反演及处理转换中的计算;而ΔT模量差与地磁场T0的方向和大小均密切相关,其与T0之间不具有线性关系特征,因而不便于一系列相应的处理计算,所以,在弱磁异常及非高精度条件下,ΔT投影具有应用上的便捷性.
(2) 地磁场T0方向和大小在勘探测区范围内可以认为是不变的,而磁性体产生的磁异常Ta的方向和大小则在测区内不同测点之间具有明显的变化;当磁异常Ta幅值大时,ΔT投影误差会比较大,并且ΔT投影误差与测点和场源的相对位置也有密切的关系,误差比例最大的测点位于磁异常Ta接近垂直于地磁场T0的区域;从当前磁力仪测量精度等指标衡量,10 nT的磁异常能引起的最大误差只有0.001 nT,100 nT的磁异常能引起的最大误差也只有0.1 nT,而1000 nT的较强磁异常能引起的最大误差就达到10 nT,5000 nT的强磁异常能引起的最大误差可达250 nT,随着磁异常的增大,误差按近似指数关系迅速增大.
(3) 应用二维柱体模型进行计算实验,结果表明:在地表实际环境下,中纬度区带的ΔT投影误差明显较大;在理论分析研究方面,二维圆柱体模型磁异常的一些属性会发生变化,例如,仅改变磁化方向为反向,两次ΔT投影曲线为严格的正负镜像关系,但ΔT模量差曲线则不具有严格对称性特征;磁性体的尺度(即半径)与埋深的比值r/R超过0.5且磁化率超过0.1 SI时误差已经达到3.9 nT.所以,强磁化磁性体产生了大幅度磁异常时,其定量处理及解释需要关注该误差因素,具体情况视精度要求而定.
综上所述,在进入高精度勘探精细处理解释阶段,ΔT计算误差是不容忽视的,特别是强磁异常而言.
本文只对该误差进行了分析研究,基于严格无误差的ΔT模量差,进行相应的处理解释,有必要继续深化,开展此项研究工作.
Blakely R J. 1996. Potential Theory in Gravity and Magnetic Applications. Cambridge: Cambridge University Press.
Clark D A. 1983. Comments on magnetic petrophysics.ExplorationGeophysics, 14(2): 49-62.
Clark D A, Emerson D W. 1991. Notes on rock magnetization characteristics in applied geophysical studies.ExplorationGeophysics, 22(3): 547-555.
Fang H Z. 1978. Calculation of a magnetic anomaly by three-dimensional bodies of arbitrary shapes in the condition of high susceptibility (in Chinese): Acta Geol.Sinica.ActaGeol.Sinica, 52(1): 63-78.
Guan Z N. 2005. Geomagnetic Field and Magnetic Exploration (in Chinese). Beijing: Geological Publish House.
Guo W W, Dentith M C, Bird R T, et al. 2001. Systematic error analysis of demagnetization and implications for magnetic interpretation.Geophysics, 66(2): 562-570.
Kontis A L, Young G A. 1964. Approximation of residual total-magnetic-intensity anomalies.Geophysics, 29(4): 623-627.
Krahenbuhl R A, Li Y G. 2007. Influence of self-demagnetization effect on data interpretation in strongly magnetic environments.ASEGExtendedAbstracts, 713-717.
Li C M, Li J. 2013. Gravity and Magnetic Prospecting Principle and Method (in Chinese). Beijing: Science Publishing House.
Li Y G, Krahenbuhl R A. 2011. A General Framework for 3D Interpretation of Magnetic Data Affected by Remanence and Self-Demagnetization.∥12th International Congress of the Brazilian Geophysical Society.
Zhang H L, Liu T Y, Zhu C J, et al. The effects of applying high-precision magnetic survey: a case study of the Galinge ore district in Qinghai province.GeophysicalandGeochemicalExploration(in Chinese), 35(1): 12-16.
Zhang H L, Hu X Y. 2012. A stable downward continuation and its application for mineral is exploration.∥2012 SEG Annual Meeting. Society of Exploration Geophysicists.
Zhu C J, Zhou Z W, Liu T Y, et al. 2011. Application of high-precision magnetic survey to prospecting: A case study in the Galinge Deposit of Qinghai Province.GeologyandExploration(in Chinese), 47(2:277-283).
Zhu Y G, Yu C C. 2006. Analysis of magnetic properties of Daye iron deposit in Hubei province.ContributionstoGeologyandMineralResourcesResearch(in Chinese), 21(S1): 155-159.
附中文参考文献
方华竹. 1978. 任意形状强磁性三度体磁异常的计算. 地质学报, 52(1): 63-78.
管志宁. 2005. 地磁场与磁力勘探. 北京:地质出版社.
李才明,李军. 2013. 重磁勘探原理与方法. 北京:科学出版社.
张恒磊, 刘天佑, 朱朝吉, 等. 2011. 高精度磁测找矿效果—以青海尕林格矿区为例. 物探与化探, 35(1): 12-16.
朱朝吉,周肇武, 刘天佑等. 2011. 高精度磁测找矿效果: 以青海尕林格矿区为例. 地质与勘探, 47(2): 277-283.
朱永刚, 于长春. 2006. 湖北省大冶铁矿区内矿石磁性特征分析. 地质找矿论丛, 21(B10): 155-159.
(本文编辑 胡素芳)
Error analysis of calculation of total field anomaly due to highly magnetic bodies
YUAN Xiao-Yu, YAO Chang-Li*, ZHENG Yuan-Man, LI Ze-Lin, WANG Jun-Heng
KeyLaboratoryofGeo-detection(ChinaUniversityofGeosciences,Beijing),MinistryofEducation,Beijing100083,ChinaStateKeyLaboratoryofGeologicalProcessesandMineralResources,Beijing100083,China
Currently, the magnetic prospecting has a great demand for high-precision processing and interpretation. In order to meet this requirement, we studied the approximate errorEbetween ΔTact(the total-field anomaly) and ΔTpro(the projection of anomalous field vector onto the direction of geomagnetic field). Generally speaking, the errorEis extremely small when the bodies have weakly magnetic susceptibilities. However, when the bodies have highly magnetic susceptibilities, the errorEmight be large. This will lead to significant effects on subsequent quantitative inference. Therefore, we investigated the errorEdue to highly magnetic bodies. In this paper, a systematic error analysis was made by using a 2-D elliptic cylinder model. We investigated the errorEthrough numerical experiments of magnetic anomalies produced by high-susceptibility bodies. Normally, for high susceptibilities, we found that the existed remanence significantly affected the errorE. The error analysis showed that the magnitude of ΔTactwas usually larger than that of ΔTpro. This implied that a theoretical anomaly computed without accounting for the errorEwould overestimate the anomaly associated with the body.we used the 2-D elliptic cylinder model to illustrate the importance of the error analysis when the bodies were highly magnetic. Firstly, we demonstrated through numerical experiments that the errorEwas obvious and should not be ignored. Secondly, we showed that the curves of ΔTproand the errorEhad a certain symmetry when the directions of magnetization and geomagnetic field changed. And we also displayed that theEmax(the maximum value of the errorE) appeared above the center of the magnetic body when the parameters such as the vector of geomagnetic fieldT0, the geometric form (e.g., the radiusrand the depthRof the 2D horizontal cylinder body) and the magnetic parameters (e.g., the susceptibilityκ) are determined, and that the relationship between theEmaxand magnetic parameters or size of the model (e.g.,r/R) is exponential. Then we discovered some other characteristics about the errorE. For instance, the curve ofEmaxwith respect to the latitude was symmetrical on both sides of magnetic equator, and the extremum of theEmaxcan always be found in the mid-latitudes. WhenT0was perpendicular toTa(the vector of the anomaly), the errorErised with the increase ofTa. Whenθ(the included angle betweenTaandT0) changed, theEmaxdue to the cylinder model is found inθ=90°~120°. Whenr/Ris larger than 0.5 and the susceptibility is larger than 0.1SI, theEmaxreaches to 3.9 nT. As a result of the numerical experiments, we concluded that when the bodies have highly magnetic susceptibilities, the errorEmay be great and will affect the subsequent magnetic processing and inversion. Therefore, the errorEcannot be ignored when the magnetic data are processed, inverted, and interpreted in highly magnetic environments.
Total-field anomaly; Approximate error; Vector of magnetic anomaly; Remanence; Susceptibility
国家高技术研究发展计划(863计划)项目(2014AA06A613)和国家自然科学基金项目(41304104)资助.
袁晓雨,主要从事重磁处理与反演研究.E-mail:792010739@qq.com
*通信作者 姚长利,主要从事重磁勘探理论与方法技术研究. E-mail:clyao@cugb.edu.cn
10.6038/cjg20151235.
10.6038/cjg20151235
P318,P631
2015-04-13,2015-10-09收修定稿
袁晓雨, 姚长利, 郑元满等. 2015. 强磁性体ΔT异常计算的误差分析研究.地球物理学报,58(12):4756-4765,
Yuan X Y, Yao C L, Zheng Y M, et al. 2015. Error analysis of calculation of total field anomaly due to highly magnetic bodies.ChineseJ.Geophys. (in Chinese),58(12):4756-4765,doi:10.6038/cjg20151235.
