混凝土灌注桩中混含硫酸盐的时变分布规律

姚明博，李镜培

(同济大学 地下建筑与工程系;岩土及地下工程教育部重点实验室,上海 20092)

混凝土灌注桩中混含硫酸盐的时变分布规律

姚明博，李镜培

(同济大学 地下建筑与工程系;岩土及地下工程教育部重点实验室,上海 20092)

硫酸盐环境下，为模拟混凝土灌注桩施工时混入的硫酸盐在桩中的时变分布行为，基于Fick第二定律并结合初始条件与边界条件，应用分离变量法，建立硫酸盐在桩中的时变分布模型。通过算例将本文解与传统解进行比较，并进一步探讨了硫酸盐扩散分布的影响因素和影响规律。结果表明，传统解用于分析混凝土灌注桩桩中硫酸盐扩散有局限性，而本文解相对于传统解具有一定的优势。混凝土灌注桩半径越小，应用传统解分析灌注桩中硫酸盐时变分布误差较大，同时，误差随时间增大。硫酸盐在混凝土灌注桩中的时变分布呈沙漏形，沿半径方向x=0处和桩表面处扩散行为明显，在x=0处附近区域，初始第一年扩散速率较快，在后续的50 a内扩散速率显著减小，但每10 a的平均速率基本相同。扩散系数和初始浓度梯度对硫酸盐在混凝土灌注桩中的时变分布影响较大。

时变分布；扩散；硫酸盐；混凝土灌注桩

硫酸盐通过扩散进入混凝土灌注桩，并与混凝土水化产物反应，使混凝土灌注桩膨胀开裂或降低混凝土胶结能力，加速了混凝土灌注桩性能劣化。因此，研究硫酸盐对混凝土灌注桩的侵蚀过程与机理显得尤为必要。在硫酸根离子扩散机理研究方面，Samson等[1]采用扩展的能斯特-普朗克模型来解释离子扩散机制，考虑化学活性效应，预测溶液中离子在化学势梯度下的扩散。Marchand等[2]考虑离子传输与化学平衡建立了数值模型，Tixie等[3-4]建立了化学-力学数学模型，Samson等[5]基于算子分裂方法建立了多离子传输模型，Sarkar等[6]采用数值方法，来模拟混凝土在侵蚀环境中的劣化。Lorente等[7]对比分析了硫酸镁和硫酸钠两种硫酸盐的迁移与扩散结果，揭示了硫酸镁扩散更慢的原因。同时，电位差对硫酸盐的迁移有显著影响，加速了混凝土的腐蚀与性能退化。Andrés等[8]建立硫酸盐环境下混凝土化学-力学有限元模型，考虑裂缝对离子传输的影响，采用基于断裂本构关系的零厚度单元，从细观角度进行扩散-反应分析。从理论解析、建立数值模型、室内试验三方面揭示硫酸根离子在混凝土中的扩散规律及影响因素。目前，对于混凝土桩中的离子扩散问题，主要研究有海水环境下的氯离子在混凝土管桩中的扩散规律[9],以及混凝土管桩的寿命理论模型及寿命预测，都涉及了氯离子在混凝土管桩中的扩散研究[10-13]。对于上述氯离子在管桩中的扩散机理以及前文中所述的硫酸盐在常规混凝土试件中的扩散机理研究，都是基于溶液中的离子从外部进入硬化成型的混凝土试件内部。而对于硫酸盐环境中的现浇混凝土灌注桩，在未硬化前则随机混入含硫酸盐的腐蚀介质，类似的内部扩散机理研究尚不多见，因此，针对此类问题的研究显得尤为必要。

为了更加切实的模拟硫酸盐环境下灌注桩中硫酸盐的内部封闭扩散行为，笔者基于Fick第二扩散定律，考虑边界不与外界发生硫酸盐的扩散，应用分离变量法和贝塞尔函数性质，建立了硫酸盐在混凝土灌注桩中任意分布的扩散模型，并与传统扩散模型进行比较，最后，通过算例分析了混凝土灌注桩中硫酸盐的时变分布行为及有关参数的影响。

1 硫酸盐在灌注桩中的分布模型解析

在硫酸盐环境条件下施工的混凝土灌注桩，不可避免的会混入硫酸盐为主的腐蚀介质。设混凝土灌注桩半径为r=a，如图1所示，初始时刻混凝土灌注桩中硫酸根离子分布为f(r)，即图1(a)中随机分布不同大小的圆圈代表硫酸盐质量浓度的随机分布。为了问题的简化，特提出以下假定：

1)不考虑灌注桩中混入的硫酸盐与混凝土水化产物发生化学反应以及外界硫酸盐的侵蚀。

2)只考虑硫酸根离子在混凝土灌注桩桩中的径向扩散，且桩边界处不可渗透，即发生扩散时桩边界处浓度梯度为零。

3)只考虑硫酸盐沿半径方向的分布，如图1(b)所示，r=x处混入的硫酸盐质量浓度最大，近似等效为以r=x处为浓度峰值的线性分布，如图1(c)，则只需要取其中一段的浓度分布分析即可，r=x处左右两侧硫酸盐质量浓度梯度不同的扩散分析详见3.3节。

图1 桩中硫酸盐随机分布简化分析图Fig.1 Schematic representation of the simplification made on stochastic distribution of sulfate in pile plane

选取单位长度的混凝土灌注桩进行分析，根据上述假定，硫酸根离子的扩散规律仅为半径r和时间t的函数。硫酸根离子在混凝土灌注桩中的扩散系数为D，依据硫酸根离子质量守恒和Fick第二扩散定律可得：

(1)

式中:u为桩中硫酸盐沿半径方向的质量浓度。式(1)的初始和边界条件为

(2)

应用分离变量法，设u(r,t)=R(r)T(t)，代入式(1)得

(3)

式中:β2为分离常数,β>0，式(3)的通解为：

(4)

式中:J0和Y0分别为第一类和第二类零阶贝塞尔函数。

由于u(r,t)的有界性，B=0，再由式(2)中的边界条件得J0′(βa)=0或J1(βa)=0。即βa是J1(x)的零点，以μn(n=1,2,…)表示J1(x)的正零点，则β=μn/a，所以取

(5)

这样,un=Rn(r)Tn(t)满足式(1)扩散方程和式(2)中的边界条件，还需同时满足J0′(βa)=0。由叠加原理，函数

(6)

也满足式(1)扩散方程和式(2)中的边界条件，根据式(2)中的初始条件得

(7)

利用贝塞尔函数的正交性，得

Cma2J02(μm)/2

(8)

(9)

式(9)即为混凝土灌注桩中硫酸盐时变分布模型解析解。

取图1(c)中x处右侧线性分布进行分析，该线性分布向左平移x单位，使x=0，即f(r)=u0(1-kr)，式(9)加号右边部分采用分部积分及引入斯特鲁夫函数解得

(10)

式中:S1为一阶斯特鲁夫函数。将式(10)代入式(9)得

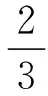
(11)

若k=a-1,带入式(11)得

u(r,t)=

(12)

2 传统三角级数解析

为了便于与本文解答进行对比，取单位长度的平板，其厚度为2a,如图2所示。板厚关于x=0对称，只考虑x方向[0,a]区间的一维扩散，硫酸盐在板边界x=a处不与外界发生扩散，板内硫酸盐沿x正方向的分布为f(x)。

图2 传统平板截面内硫酸盐随机分布Fig.2 Stochastic distribution of sulfate in slab plane

根据初始条件与边界条件、离子质量守恒与Fick第二扩散定律可得

(13)

结合边界条件和初始条件[15]得解为

(14)

同理，f(x)=u0(1-x/a)，式(14)进行积分得

(15)

式中：n=2m+1,m=0,1,2,…。

3 算例及影响因素分析

3.1 与传统三角级数解答的比较

混凝土灌注桩半径为250mm，相当于平板厚度为500mm，扩散系数D按文献[3]取值为10-12m2/s，经单位换算后约为32 mm2/a，x=0处初始质量浓度u0为3%。分别取扩散时间为1、10、20、50、100a，灌注桩半径为50、150、250mm，按照本文方法和传统三角级数解答进行计算，并进行交叉对比，如图3所示。当扩散时间为1a时，如图3(a)所示，两种解析得出的硫酸盐质量浓度分布吻合度比较高，硫酸盐质量浓度分布差异性不明显，尺寸效应对硫酸盐质量浓度分布的影响亦不明显。当扩散时间为10a时，如图3(b)所示，两种解析得出的硫酸盐质量浓度分布差异性明显，传统解得出的质量浓度分布略高，平均扩散速率更慢；而随着混凝土灌注桩半径的减小，两种解得出的硫酸盐质量浓度分布差异性增大，尺寸效应影响明显。20～100a的时间节点上，如图3(c)、(d)、(e)所示，同尺寸的两种解答得出的硫酸盐质量浓度分布差异性随时间进一步增大，尺寸效应影响更加明显。当扩散时间为100年时，在现有假设条件下，随着灌注桩半径成倍增大至1 000mm时，两种解答差异又逐渐减小至接近可忽略的程度，如图3(f)所示。根据图3(d)、(e)、(f)的解析结果可以看出，当灌注桩桩半径较小时，传统解法应用于灌注桩中的硫酸盐扩散分析与本文解的差异较大，形状因素对传统解析所得的结果影响较大；灌注桩半径足够大时，桩的形状因素对传统解的影响可以忽略。因此，灌注桩的形状和尺寸大小对传统解析所得结果的影响是相互制约的，传统解适合于圆柱桩中硫酸盐的初期扩散分析以及尺寸足够大的圆柱桩中硫酸盐扩散分析，因而具有局限性。

图3 硫酸盐解析分布对比Fig.3 Comparison of sulfate analytical distributions

综上所述，硫酸盐扩散分布的解答与扩散域的形状密切相关；同时，传统解法应用于灌注桩中硫酸盐的扩散分析，与本文解相比，受扩散时间和桩尺寸制约。混凝土灌注桩与常见的梁、板等平面结构形式不同，其硫酸盐在混凝土灌注桩中的扩散行为也会有所差别；尺寸越小，硫酸盐在两种扩散域的扩散行为差异性越大。因此，针对传统解用于圆柱形桩中硫酸盐扩散分布分析的局限性，本文解的提出有助于更加准确分析硫酸盐在圆柱形桩中的扩散分布行为。

3.2 灌注桩中硫酸盐时变分布规律

图4 灌注桩中硫酸盐初始线性分布的时变分布Fig.4 Time-varying distribution of sulfate in bored pile with the initial linear distribution of sulfate

当灌注桩中硫酸盐分布是线性分布时，由式(11)得出不同扩散时间下的质量浓度分布，并与初始质量浓度分布进行比较，如图4所示。在x=0，硫酸盐初始质量浓度最大，为3%。由于桩中沿半径方向初始硫酸根质量浓度梯度较大，扩散速率较快，x=0处硫酸盐质量浓度减少量为0.3%，为初始质量浓度的1/10。在1a后的50a内，随着x=0处硫酸根离子在桩中不断扩散，硫酸盐质量浓度梯度减小，扩散速率大大降低，但扩散速率比较稳定，每一年的硫酸盐质量浓度降低量大约为0.01%，为初始质量浓度的1/300。第2个50a间的扩散速率，与第1个50a间的平均扩散速率相比略有下降，每一年的硫酸盐质量浓度降低量为0.008%。对于桩身表面处，初始硫酸盐质量浓度为零。在初始扩散阶段的1a内，同理，桩表面处硫酸盐质量浓度增加量为0.3%，为初始质量浓度的1/10。但硫酸盐在后续的扩散过程中，桩身表面处硫酸盐质量浓度的增加规律不够明显。另外，从图4中可以得知，灌注桩中的硫酸盐时变分布整体呈沙漏型，随着时间的变化，x=0处与桩表面的硫酸盐质量浓度差减少，整体硫酸盐质量浓度梯度减小；大概在离桩轴心为0.6r处有一个硫酸盐质量浓度不变点，犹如沙漏的中间通道，在空间表现为临界质量浓度通过面。

3.3 灌注桩中硫酸盐不同质量浓度梯度的分布规律

扩散速率大小与浓度梯度大小有关，取k=0.5 a-1，t=20 a。从图5中可以得出，不论质量浓度梯度大小，[0,50]和[200,250]范围内两区间的梯度变化较大， 扩散作用明显。剩余区域硫酸盐质量浓度梯度变化不明显，质量浓度略有下降。另外，质量浓度梯度越大，两端区域扩散速率越大，质量浓度变化量越大。

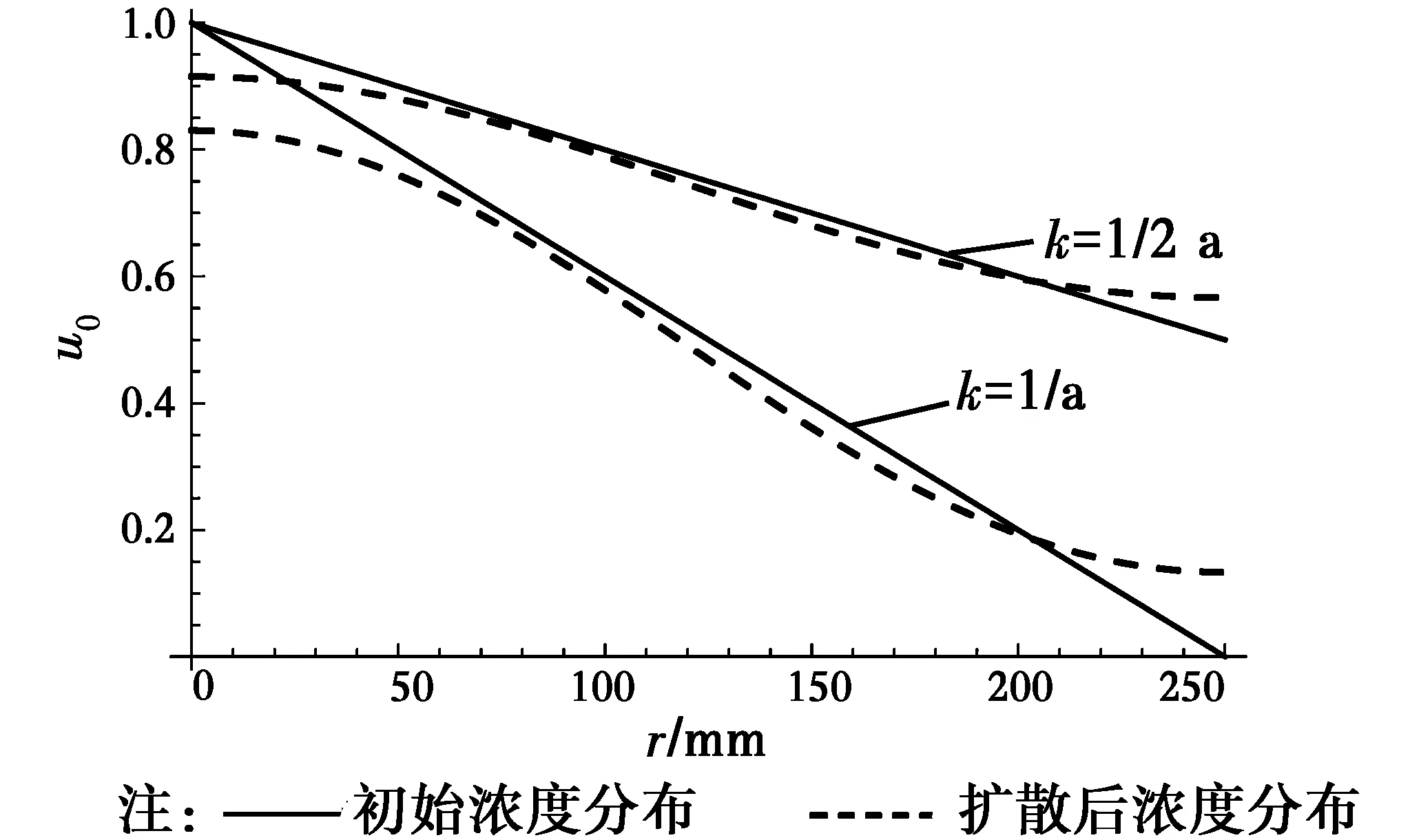
图5 不同质量浓度梯度的硫酸盐分布Fig.5 Sulfate distribution with different concentration gradients

3.4 扩散系数不同时灌注桩中硫酸盐分布规律

硫酸盐在混凝土材料中的扩散系数取值范围[4]为(0.75～9)×10-12m2/s,在此范围内扩散系数取值32、62、92 mm2/a进行分析，t=20 a。如图6所示，在同一时间内，硫酸盐扩散系数越小，单位时间内的硫酸盐扩散量越小，质量浓度梯度越大。因此，硫酸盐扩散系数大小对硫酸盐在灌注桩中的扩散影响比较显著。

图6 不同扩散系数的硫酸盐分布Fig.6 Sulfate distribution with different diffusion coefficients

4 结 论

建立了混入混凝土灌注桩中的硫酸盐在桩中的封闭扩散模型，并与传统解析比较，得出了两种解答的一致性与差异性，表明传统解法应用于混凝土灌注桩中具有局限性，且通过算例分析了硫酸盐在灌注桩中的时变分布规律以及参数影响，得出如下结论。

1)当灌注桩尺寸越大，或硫酸盐在混凝土灌注桩中的扩散时间越短，尺寸效应对硫酸盐在灌注桩中的时变分布影响越小，本文解与传统解两者具有很高的一致性，吻合度很高；反之则具有一定的差异性，由此进一步表明，硫酸盐的扩散行为与域密切相关。

2)灌注桩中硫酸盐的初始质量浓度梯度一定，随时间增加，质量浓度梯度不断减小，梯度越大，初期扩散作用越明显；硫酸盐在x=0处初始一年内平均扩散速率较快，在后续的50a内平均扩散速率趋于稳定，桩身表面附近区域规律不明显。

3)硫酸盐在混凝土灌注桩中的时变分布呈沙漏形，桩中硫酸盐质量浓度差随时间不断减小，扩散系数越大，硫酸盐越容易在更短时间内扩散均匀。

硫酸盐与混凝土水化产物发生化学反应是影响硫酸盐在混凝土灌注桩中分布的一个非常重要的因素，也是导致混凝土结构耐久性退化、服役寿命缩短的重要环境因素之一，在后续的研究中，有待对硫酸盐在灌注桩中的反应-扩散进一步深入，以及考虑内外扩散腐蚀对桩中硫酸盐分布的影响。

[1] Samson E,Marchand J. Numerical solution of the extended nernst-planck model [J]. Journal of Colloid and Interface Science,1999,215(1): 1-8.

[2] Marchand J,Samson E,Maltais Y,et al. Theoretical analysis of the effect of weak sodium sulfate solutions on the durability of concrete[J]. Cement and Concrete Composites,2002,24(3/4): 317-329

[3] Tixier R,Mobasher B. Modeling of damage in cement-based materials subjected to external sulfate attack II: Comparison with experiments[J]. Journal of Materials Civil Engineering,2003,15 (4):314-322.

[4] Tixier R,Mobasher B. Modeling of damage in cement-based materials subjected to external sulfate attack I: Formulation[J]. Journal of Materials Civil Engineering,2003,15 (4):305-313.

[5] Samson E,Marchand J. Modeling the transport of ions in unsaturated cement- based materials[J]. Computers & Structures,2007,85 (23/24): 1740-1756.

[6] Sarkar S,Mahadevan S,Meeussen J C L,et al. Numerical simulation of cementitious materials degradation under external sulfate attack [J]. Cement and Concrete Composites,2010,32(3): 241-252.

[7] Lorente S,Yssorche-Cubaynes M,Auger J. Sulfate transfer through concrete: Migration and diffusion results[J]. Cement and Concrete Composites,2011,33 (7):735-741.

[8] Andrés E I,Carlos M L,Ignacio C. Chemomechanical analysis of concrete cracking and degradation due to external sulfate attack: A meso-scale model [J]. Cement and Concrete Composites,2011,33(3): 411-423.

[9] 李镜培,杨博,岳著文. 氯离子在混凝土管桩中的扩散规律[J]. 土木建筑与环境工程,2013,35(4): 79-83. Li J P,Yang B,Yue Z W. Diffusion behavior of chloride ions in concrete pipe pile[J]. Journal of Civil,Architectural & Environment Engineering,2013,35(4):79-83.(in Chinese)

[10] Li J P,Shao W. The effect of chloride binding on the predicted service life of RC pipe piles exposed to marine environments [J]. Ocean Engineering,2014,88:55-62.

[11] Shao W,Li J P. Service life prediction of cracked RC pipe piles exposed to marine environments [J].Construction and Building Materials,2014,64:301-307.

[12] 邵伟，李镜培,岳著文. 氯离子侵蚀混凝土管桩寿命预测理论模型[J]. 硅酸盐学报,2013,41(5): 575-581. Shao W,Li J P,Yue Z W. Service life prediction of concrete pipe pile due to chloride ion corrosion by modeling[J]. Journal of the Chinese Ceramic Society,2013,41 (5): 575-581.(in Chinese)

[13] 邵伟,李镜培. 海洋环境下带裂缝PHC管桩中钢筋锈蚀 初始时间预测[J]. 土木工程学报,2014,47(3): 123-129. Shao W,Li J P. Prediction on corrosion time of embedded steel in cracked PHC piles exposed to marine environments[J]. China Civil Engineering Journal,2014,47 (3):123-129.(in Chinese)

[14] Carslaw H S,Jaeger J C. Conduction of heat in solids [M].Oxford: The Clarendon Press,1959.

[15] Crank J. The mathematics of diffusion[M]. Oxford: The Clarendon Press,1975.

(编辑 王秀玲)

Theoretical analysis of the time-varying distribution behavior of bored pile internal mixed sulfate

YaoMingbo,LiJingpei

(Department of Geotechnical Engineering;Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education,Tongji University,Shanghai 200092,P.R. China)

The time-varying distribution behavior of sulfate with diffusion is investigated for bored pile internal mixed corrosion at different amounts of service times. The formulation of diffusion,based on Fick-second law combined with the initial condition and the boundary condition,for sulfate in the bored pile is formed with the method of separation of variables. A model of concrete pile is offered as an example for illustrating the time-varying distribution behavior of sulfate and making comparison with the traditional model. Further,the influence factors and their effects on the sulfate diffusion distribution are also analyzed. The results show that the application of traditional method in analysis of sulfate diffusion in bored pile has some limitations and advantages of the proposed method are obvious. The radius of bored pile decreasing induces the discrepancy of sulfate distribution increasing with employing the traditional method,while the discrepancy increases over time. The time-varying distribution of sulfate in bored pile resembles hourglass figure that along the radius direction,diffusion behavior atx=0 and surface of pile is significant. In the region nearx=0,the diffusion rate of sulfate is fast during the first year and then the diffusion rate is dramatically reduced to constant rate during the 50 years. Diffusion coefficient and the concentration gradient of sulfate in bored pile have a pronounced effect on the time-varying distribution of sulfate.

time-varying distribution; diffusion; sulfate; bored pile

10.11835/j.issn.1674-4764.2015.05.014

2015-06-12 基金项目：国家自然科学基金(51178341)

姚明博(1987-)，男，博士,主要从事桩基耐久性研究,(E-mail)supersonic3035@qq.com。 李镜培(通讯作者)，男，教授,(E-mail)lijp2773@tongji.edu.cn。

Foundation item：National Natural Science Foundation of China(No.51178341)

TU528

A

1674-4764(2015)05-0095-06

Received:2015-06-12

Author brief：Yao Mingbo (1987-),PhD candicate,main research interest:durability of pile foundation,(E-mail)supersonic3035@qq.com. Li Jingpei (1963-),professor,(E-mail)lijp2773@tongji.edu.cn.