时延情形下分布式Push-sum次梯度优化算法的研究
2015-05-11李德权张晓倩
李德权,张晓倩
(安徽理工大学理学院,安徽 淮南 232001)
时延情形下分布式Push-sum次梯度优化算法的研究
李德权,张晓倩
(安徽理工大学理学院,安徽 淮南 232001)
针对多个体系统在个体间进行信息交换时发生接收信息滞后,存在通信时延,影响优化算法的收敛速度的问题,提出一种时延情形下的分布式Push-sum次梯度优化算法,该方法在权矩阵不具有正对角线元素时仍适用,并应用系统扩维的方法将有时延优化问题转化为无时延优化问题。在时延和次梯度有界且有向切换网络周期强连通的条件下,证明了所提出的分布式Push-sum次梯度优化算法的收敛性。研究表明:存在通信时延时的算法收敛速度比无时延时的收敛速度要慢,并具有较大的收敛误差。最后,通过数值仿真验证了研究的结论。
时延;Push-sum算法;次梯度;分布式优化
近年来,基于局部信息交互协同的整个网络的优化问题成为多个体网络新的研究热点[1-2],因而引起了众多学者的广泛兴趣。科学与工程领域的众多问题,如大规模机器学习、分布式跟踪与定位等,都可以归类于多个体网络分布式优化问题。目前分布式优化算法主要分为三种:原始优化算法[3]6 857,对偶优化算法,原始-对偶优化算法,且这三种优化算法通常解决的问题具有如下特点:整个网络优化的目标函数可以分解成网络中各个个体的目标函数之和,每个个体仅知道其自身的目标函数,且只能通过和其邻居个体信息交互协同地解决整个网络的问题,即此时所有个体状态趋于一致且这个一致性值还是网络优化问题目标函数的最优解[4]。由于分布式优化问题涉及到个体间的局部信息交互,因而与多个体网络的一致性问题,特别是平均一致性(即每个个体状态收敛到所有个体初始状态的算术平均值)密切相关。目前一致性的研究主要分为基于单变量信息通信[5]和双变量信息通信两类。单变量信息通信即个体间交互的仅是某一个状态变量,目前绝大部分多个体网络一致性的研究是基于单变量信息通信,但其缺点是,只有有向平衡网络中的个体才能达到平均一致性,这要求网络对应的邻接矩阵必须是双随机矩阵,因而具有很大的局限性。但实际多个体网络通常是动态切换、有向非平衡的,这就需要用到双变量信息通信。因此,基于双变量信息通信的Push-sum算法的一致性研究近年来引起学者的极大兴趣,Push-sum一致性算法并不要求网络是有向平衡的,但要求网络中每个个体有两个状态变量,每次迭代交互的是这两个状态变量的比值。
当个体间进行信息交换时,信息会因为网络拥塞或受实际通信设备的影响,不能及时的送达接收端,即出现信息接收滞后的情况,这导致多个体网络信息传递产生时延。因此对有时延的多个体网络的一致性研究成为一个热点。在时延有界的情况下,文献[6-7]分别研究了一致性问题、受限一致性问题和平均一致性问题,其共同之处均是随机邻接矩阵需具有正对角元素,但当随机邻接矩阵需不具有正对角元素时,这些方法均不再适用。
在上述文献的基础上,针对个体间信息交互存在通信时延情形的分布式优化问题,本文提出一种分布式Push-sum次梯度优化算法,首先通过增加虚拟的网络节点即通过系统扩维的方法,将有通信时延的优化问题转化为无通信时延的优化问题。在时延、次梯度有界和有向网络一致强连通的条件下,证明了所提出的Push-sum次梯度优化算法的收敛性。研究表明所提算法的收敛速度比无时延情形慢且有较大的收敛误差,亦即当个体间通信时延有界时所有个体会收敛到最优解,但是时延影响了个体达到最优解的速度。
1 符号说明
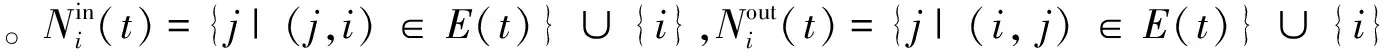
2 具有时延的优化问题
在具有n个个体的有向切换网络中,每个个体有其自身的凸函数fi(zi(t)):Rd→R,其中zi∈Rd的为决策变量。考虑以下关于整个网络的凸优化问题:
subject toz∈Rd
(1)
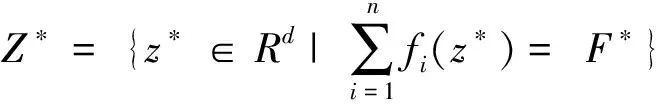
当个体间信息交互不存在通信时延时, 文献[3]6 856提出一种Push-sum分布式次梯度优化算法并分析了其收敛性。但由于网络中信息的同步交互会引起网络阻塞从而产生时延。因此,当个体间信息通信存在时延时,针对式(1)提出如下的Push-sum次梯度优化算法,其迭代格式如下:
zi(t+1)=wi(t+1)/yi(t+1)
xi(t+1)=wi(t+1)+εi(t+1)
(2)
式中:wi(t)∈R,yi(t)∈R,xi(t)∈R,xi∈R(1,…,n)为网络中个体i在t时刻的状态值;zi(t)为一个比值;A(t)=(aij(t))n×n为网络拓扑所对应的随机邻接权矩阵;τij(t)为t时刻个体j到个体i的通信时延,当所有τij(t)=0时,式(2)即退化为文献[3]所研究的情形;εi(t)=-αi(t)gi(t),i=1,…,n为第i个个体的摄动;αi(t)为t时刻个体i的迭代步长。
假设初始条件wi(0)=1,zi(0)=1,yi(0)=1,i=1,…,n。则式(2)表示为以下矩阵形式:
w(t+1)=A(t)x(t-τ(t))
y(t+1)=A(t)y(t-τ(t))
zi(t+1)=wi(t+1)/yi(t+1)
x(t+1)=w(t+1)+ε(t+1)
(3)
假设:
1) 邻接矩阵A(t)是一个具有正对角线元素的随机矩阵,即对所有i∈V和t≥0,一直成立aii=1-∑aij(t)>0;
2) 每个个体的目标函数fi(t)是凸函数且集合Z*=argminz∈RdF(z)非空;
3) 存在常数Li<∞使得‖gi‖2 4) 存在一个正整数B≥1,有向联合图(V,E(t)∪V,E(t+1)∪…∪V,E(t+B-1)),t≥1是强连通的; 对系统中每个个体的每个状态变量进行重新定义,令 (4) 引理1[7]假设1、假设4成立,令Ψ(k,s)=[Φ(k)Φ(k-1)…Φ(s)]T,则可得以下结论: b) 存在正整数v和0<α<1,对于任意的i,j∈{1,…,n(q+1)}和任意的k≥s,有下式成立: ‖[Ψ(t,s)]ij-φ(s)‖≤ 定理1 对于序列{zi(t)},i=1,…,n由式(4)迭代产生,假设1成立,有如下结论成立: a) 存在δ>0,正整数v和0<α<1,有 证 明 由文献[3]可知,无时延的Push-sum算法成立 w(t+1)=φ(t)1Tx(t)+(A(t,0)- y(t+1)=φ(t)n+(A(t,0)-φ(t)1T)1 则带有时延的算法可以写为 各组计量资料以均数±标准差表示,两组间采用t检验进行均值的比较;多组间采用单因素方差分析进行比较,数据分析使用SPSS统计分析软件,P<0.05为差异有统计学意义。 (5) zi(t+1)=wi(t+1)/yi(t+1),则有下面不等式成立 (7) 即定理1a得证。 (8) 证 明 因为 (9) 并且由定理1可知 (10) 所以推论1得证。 下面证明文中两个重要的结论,即在通讯时延有界和其它假设成立的情况下Push-sum次梯度优化算法的收敛性。 (11) 证 明 由式(10)可得 (12) 又根据文献[3]6 859引理13可得 (13) 证明 由推论1可得下式 因为 由定理2~定理3可知,本文所提出的带有时延的Push-sum次梯度优化算法在有向切换网络中是收敛的,且收敛速度取决于网络中的个体数目n和时延上界q,而在无时延情形下可知收敛速度只取决于网络中的个体数目n[6]。与文献[6]中的收敛速度相比较,因为n,q≥1,所以带有时延的算法收敛速度要稍慢,从整个多个体系统来看,虽然时延有界个体会收敛到最优解,但是时延影响了个体达到最优状态的速度,使得系统运行效率降低,即在一般的多个体网络中信息传递要比理想的、不带时延的网络中的信息传递要慢。 在理论上已证明了时延对分布式优化算法收敛性的影响,现将通过仿真验证理论结论。假设有三个个体的周期切换网络(见图1),并设周期B=3。在一个周期内每个子图都是非平衡且不连通的,但在一个周期内这三个子图的并是强连通的。 设目标函数以实数集上的二次函数为例,网络中个体所对应的函数fi(z)=(z-ai)2,ai∈R,i=1,2,3,增加的虚拟节点即时延个体所对应的函数fj(z)=0,j=4,5,6,其中ai为随机选取的实数。假设在图1a中各边的权值为a11=0.8,a21=0.2,a22=a33=1,τ12=1;图1b中a22=a23=0.5,a11=a33=1,τ32=1; 图1c中a31=0.3,a33=0.7, a11=a22=1,τ31=1。则权矩阵A(t)满足假设1。 应用MATLAB软件运行有时延和无时延情形的Push-sum分布式次梯度优化算法,绘制网络的凸优化目标轨迹如图2所示,该优化算法在有时延和无时延的情况下均会收敛到最优状态,但有一定的误差。图2还表明由于存在通信时延,本文所提算法的收敛速度比文献[3]中无时延情形的算法的收敛速度要慢。 针对存在通信时变时延情形的有向切换网络的一类优化问题,在文献[6-7]的研究基础上提出了时延Push-sum次梯度优化算法次梯度优化算法。并假设1~假设4成立且邻接矩阵是列随机矩阵时,证明了当网络中通信时延有界时所提出的分布式优化算法收敛,并通过仿真验证了所提算法的有效性。 [1]GHARESIFARDB,CORTESJ.Continuous-timedistributedconvexoptimizationonweight-balanceddigraphs[C]//51thIEEEAnnualConferenceon.DecisionandControl, 2012:7 451-7 456. [2]TSIANOSKI,LAWLORS,RABBATMG.Consensus-baseddistributedoptimization:Practicalissuesandapplicationsinlarge-scalemachinelearning[C]//50thIEEEAnnualAllertonConferenceon.Communication,ControlandComputing(Allerton), 2012:1 543-1 550. [3]NEDICA,OLSHEVSKYA.Distributedoptimizationovertime-varyingdirectedgraphs[C]// 52thIEEEAnnualConferenceonDecisionandControl,2013.6 855-6 860. [4]FIUTZELERF,CIBLATP,HACHEMW.AnalysisofSum-Weight-likealgorithmsforaveraginginWirelessSensorNetworks[J].IEEETransactionsonsignalprocessing, 2013,61(11):2 802-2 814. [5]DIMAKISADG,SARWATEAD,WAINWRIGHTMJ.Geographicgossip:Efficientaveragingforsensornetworks[J].IEEETransactionsonSignalProcessing, 2008,56(3): 1 205-1 216. [6]LINP,RENW.Distributedconstrainedconsensusinthepresenceofunbalancedswitchinggraphsandcommunicationdelays[C]//52thIEEEAnnualConferenceonDecisionandControl, 2012: 2 238-2 243. [7]HADJICOSTISCN,CHARALAMBOUST.AverageConsensusinthePresenceofDelaysinDirectedGraphTopologies[J].IEEETransactionsonAutomaticControl, 2014, 59(3):763-768. [8]NEDICA,OZDAGLARA.Convergencerateforconsensuswithdelays[J].JournalofGlobalOptimization, 2010, 47(3): 437-456. (责任编辑:何学华) Distributed Push-sum Subgradient Optimization Algorithm under Time-varying Communication Delay LI De-quan,ZHANG Xiao-qian (School of Science, Anhui University of Science and Technology, Huainan Anhui 232001, China.) The distributed optimization problem in directed switching networks with time-varying delay communication among the agents was studied. Due to delay may happen when agents communicate with each other in the multi-agent system, this paper proposes a distributed Push-sum subgradient optimization algorithm in the context of communication delays, which will affect the convergence rate of optimization algorithm. Then based on state augmentation method, the analysis is carried out by reducing the optimization problem with delays to a problem without delays and this algorithm does not require the diagonal elements of the adjacency matrix are all positive.Under the assumptions that communication delays and the subgradients are bounded, and the switching directed networks are periodically strongly connected, we prove that the convergence of the proposed distributed Push-sum subgradient optimization algorithm. It is shown that the convergence rate in the case of communication delays is slower than that without communication delays, and meanwhile the proposed algorithm may bring out large convergence error. Finally, the conclusion is verified by numerical simulation. time-varying delays; Push-sum algorithm; subgradient; distributed optimization 2014-12-16 国家自然科学基金资助项目(61472003);国家自然科学青年基金资助项目(11401008);安徽省教育厅自然科学研究重点资助项目(KJ2014A067)资助。 李德权(1973-),男,安徽肥东人,教授,博士,研究方向:分布式优化理论与应用。 TP13 A 1672-1098(2015)02-0006-07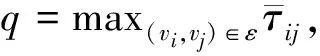
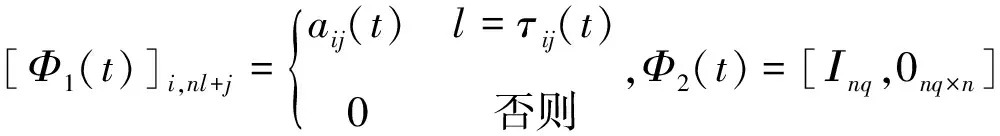
3 时延情形下的Push-sum算法收敛性


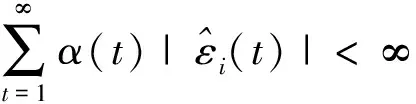

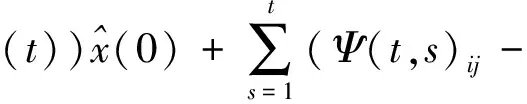

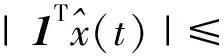
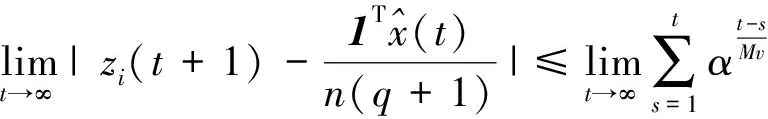
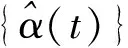
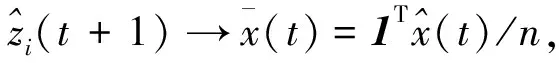
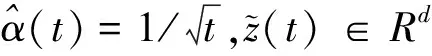
4 仿真实验
5 结束语
