瞬变电磁测井实验研究

臧德福 张福明 毛 彤 沈建国

(1.中石化胜利石油工程有限公司测井公司 山东 东营 257096；2.中国石油集团长城钻探工程有限公司测井公司 北京 100101；3.天津大学电子信息工程学院功率超声实验室 天津 300072)



·试验研究·

瞬变电磁测井实验研究

臧德福1张福明1毛 彤2沈建国3

(1.中石化胜利石油工程有限公司测井公司 山东 东营 257096；2.中国石油集团长城钻探工程有限公司测井公司 北京 100101；3.天津大学电子信息工程学院功率超声实验室 天津 300072)

文章给出瞬变电磁测井原理的实验验证。用外径为113 mm、壁厚6 mm、长1 m的有机玻璃管模拟裸眼井井眼、用外径350 mm、壁厚10 mm的粗有机玻璃管模拟地层，粗有机玻璃内放置盐水模拟地层的电阻率，用长1 m的5.5 in(1 in=25.4 mm)套管制作套管模型井，同样，用直径300 mm、壁厚10 mm的粗有机玻璃管模拟地层。自制发射和接收线圈，用间距150 ms的方波激发，测量不同源距的接收波形，获得了瞬变电磁响应随源距的衰减规律。改变盐水的电阻率重新测量，用不同地层电阻率的响应相减抵消瞬变电磁激发响应的一次场，获得了直接反映地层电阻率的二次场响应波形。实验发现：理论计算的二次场响应波形特征与实验结果一致，即裸眼井的二次场在瞬变激发的两侧(通断前后)均有极值，而且符号相反；套管井的二次场仅仅在一侧有极值。但是，由于激发电路衰减常数的影响，实际测量的二次场波形在电流突变一侧的幅度大，在指数衰减一侧的幅度小。裸眼井的二次场幅度远远大于套管井的二次场幅度，套管井地层电阻率测量的原始信号很小。

瞬变电磁测井；实验；模型井；二次场；衰减规律

0 前 言

瞬变电磁测井原理研究给出了瞬变激发的一次场和二次场响应波形。这些波形特征为我们理解瞬变电磁测井原理、设计瞬变电磁测井仪器提供了重要的理论基础[1～4]。理论研究建立在理想的瞬变激发基础上，认为突变是在瞬间完成的，不考虑瞬变激发的衰减过程，因此，理论响应是理想的，是仪器设计努力的方向。

实验同样是重要的，实验不但能够验证理论计算结果，还能够给出仪器实现与理论之间的差别，展现仪器设计面临的具体困难。对瞬变电磁测井来讲：用大电流的通断激发瞬变电磁场，最有效地激发只能够在大电流通或断的瞬间完成，当通断结束以后，电路响应以一阶电路的指数衰减规律出现，该指数衰减导致其一次场缓慢变化，其产生的二次场幅度非常小，很难测量。这一点与瞬变电磁套管井套管厚度测量有根本区别。套管厚度测量采用的是一次场响应，测量的是指数衰减过程中所包含的套管信息。

1 实验装置

图1所示为瞬变电磁测井原理研究模型井。中间的有机玻璃管或钢套管是空的，有机玻璃管和钢套管外面充满盐水，模拟不同地层的电阻率。发射线圈和接收线圈分别固定在一个塑料管子上，能够沿z轴上下移动或者固定在z轴上，有多个不同参数的线圈用于接收瞬变电磁信号。其中：发射线圈长15 cm位于最下面，直流电阻42.8 Ω；近测量线圈长15 cm，直流电阻1.9 Ω；远接收线圈长15 cm，直流电阻2.1 Ω。水深92 cm，水的电阻率7.68 Ω·m。

实验采用的电路如图2所示，G1、G2、G3、G4分别是两对对管(参数相近的两组三极管)，G1和G4同时导通，线圈中的电流从左向右流动，称为正向导通；G2和G3同时导通，线圈中的电流从右到左流动，称为反向导通，Rs是发射线圈的串联等效电阻，L是等效电感，R是并联电阻。

实验过程分三步。第一步：测量裸眼井、套管井响应波形形状。第二步：固定发射探头，移动接收探头，测量响应波形随源距的衰减规律。第三步：固定发射和接收探头，改变盐水的电阻率测量不同地层电阻率的响应波形。

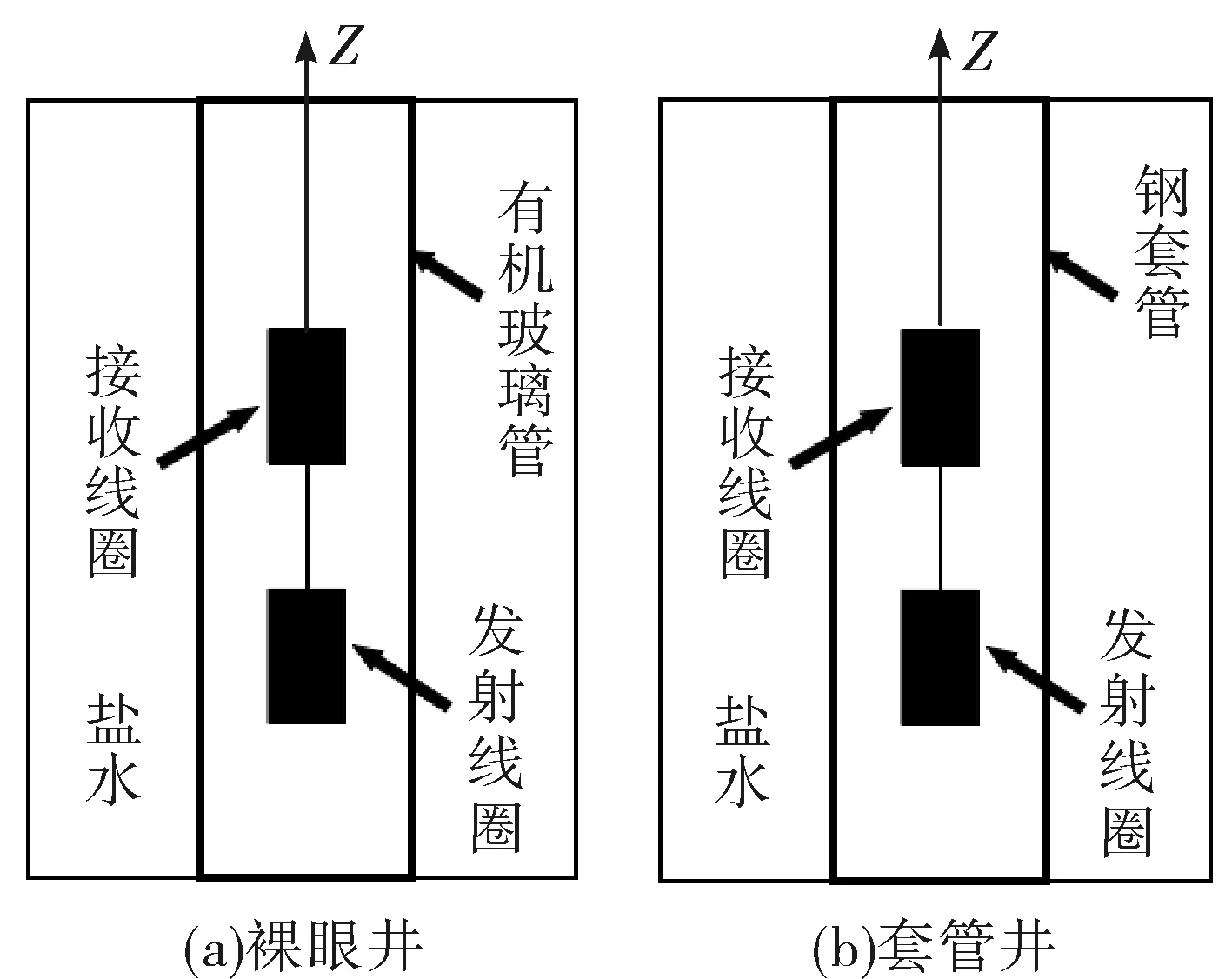
图1 瞬变电磁测井原理研究模型井

图2 实验用激发电路示意图

2 裸眼井、套管井实验波形

图3所示是在裸眼模型井(有机玻璃)测量的原始波形，图中有两个波形，分别是两个源距不同(0.15 m、0.3 m)的线圈同时测量到的，是瞬变电磁激发时在接收线圈所感应的波形。两个波形的幅度有差异，但是形状相似。从左边开始向下有两个峰值，幅度差别不大，第三个峰向上、幅度最大，接着出现一个小的正峰，这四个峰值构成一个周期，其它波形以该周期重复。四个峰值依次对应的激发波形为：反向截止、正向导通、正向截止和反向导通。其中，正向截止感应的信号最强，反向导通感应的信号小于正向导通的感应信号，所以，反向截止的感应信号小于正向截止的感应信号。

从波形上还可以看出：正向和反向导通时，感应信号随时间衰减的比较慢；正向和反向截止时，感应信号衰减的比较快。这是因为，导通时，发射线圈L与其串联等效电阻Rs的瞬态响应决定了响应波形形状；关断以后，发射线圈L中储存的电能量通过Rs和R放电，其时间常数比较小。即关断瞬间，来自三极管G1的电流减小，由于电感上的电流不能够突变，为了保证电感电流保持不变，电阻R上必然有电流向左流动，以便满足基尔霍夫电流定律。这样，电阻R上会产生电压，左负右正，该电压加到电感线圈上使线圈的电流快速减小，在此过程中，向地层辐射电能量。

图3 裸眼模型井两个不同源距的响应波形

图4是套管模型井中的激发波形(最上面的线)和三个不同源距的线圈所接收到的响应波形。从激发波形上可以看出：第一个突变位置(最左端)为正向导通，第二个位置(128 ms位置)为正向截止，第三个位置(248 ms位置)为反向导通，其导通电压比较低，第四个位置(365 ms位置)为反向截止，之后激发电压回到0的位置。图中三个不同源距线圈的响应波形的形状差异很大，第二通道的曲线的源距为0.15 m，第三通道的曲线的源距为0.30 m，第四通道的曲线为0.45 m，随着源距的增加，响应的极大值位置向右移动，极大值前面的曲线上升变缓慢。该结果提示我们，套管井内，在现有的激发方式和电路中，不同源距的接收波形形状差异明显，接收波形形状随源距改变，这是金属套管高电导率和高磁导率对瞬变电磁屏蔽作用的具体表现。

图4 套管模型井的实验波形

3 不同源距的实验波形

其它条件不变，仅仅改变源距测量其中一个线圈的响应波形得到图5所示的波形。图中不同源距的波形绘制时人为地向上移动了一定距离，源距的变化范围是15 cm～60 cm，最下面的黑线是最近源距的接收线圈所接收到的波形，测量过程中保持不变；其它黑线是另外一个线圈在源距逐渐增加时所测量到的响应波形。从图中可以看到：随着源距的增加，整个波形的幅度在减小，峰值的最大值向后慢慢移动。

我们将响应波形中第一个极大峰值取出，并按照源距进行指数拟合发现：其幅度随源距的变化规律满足指数规律，如图6、图7所示。裸眼井的幅度比较大，也满足指数规律。该结论与理论计算结果吻合，图8是理论计算的套管井响应最大值随源距的变化规律，在半对数刻度下是一条直线。

4 不同地层电导率的实验波形

在有机玻璃模型井内固定发射、接收探头之间的距离，改变盐水的电导率，模拟不同地层电导率进行实验，

图5 不同源距所接收到的响应波形

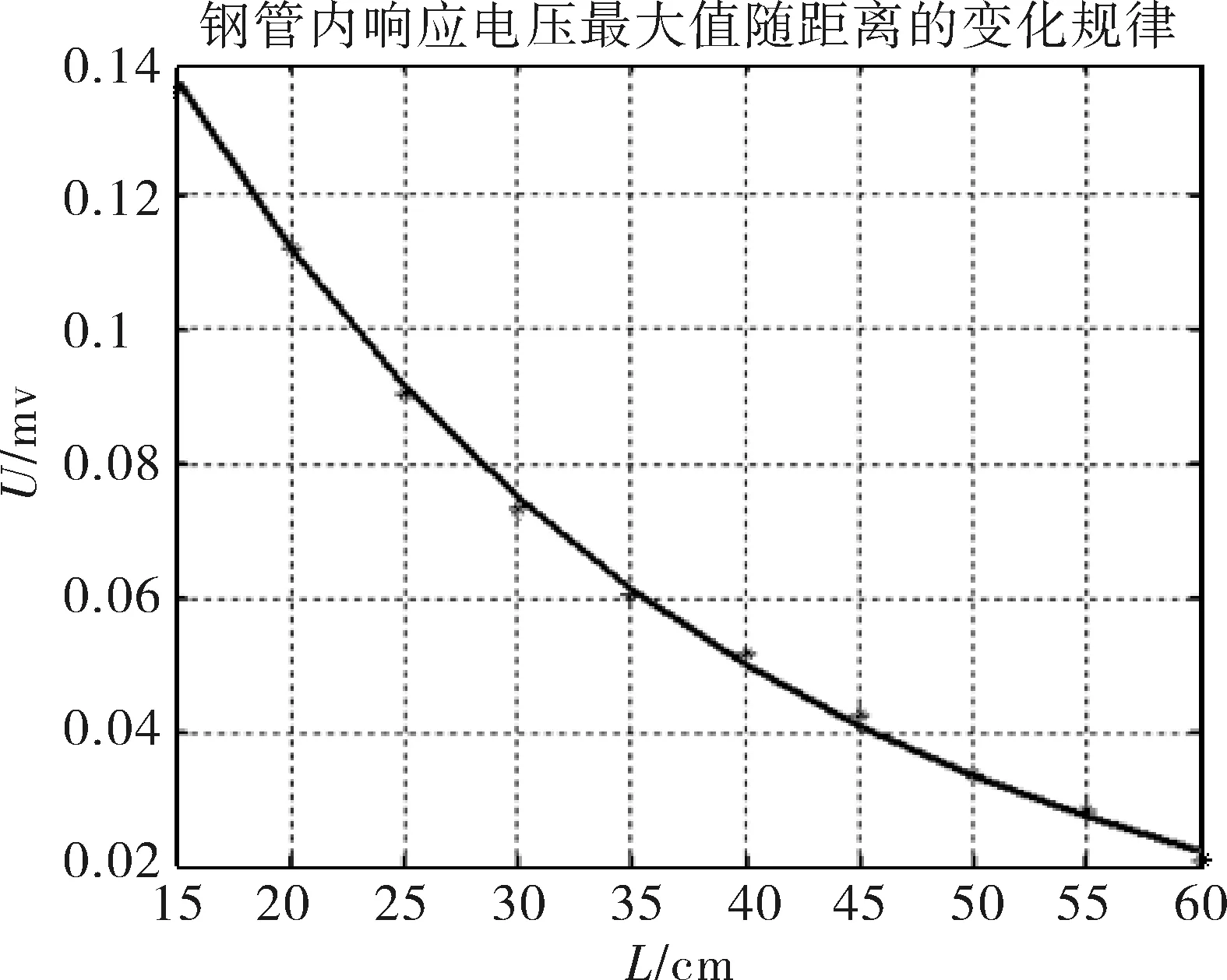
图6 钢套管模型井响应幅度随源距的衰减规律

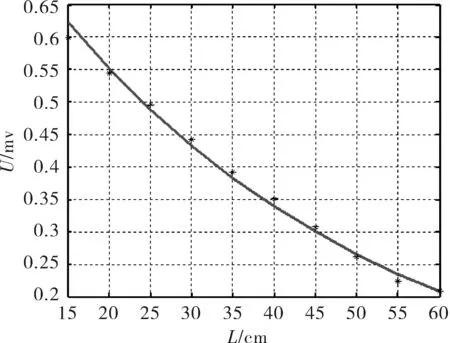
图7 玻璃钢模型井响应幅度随源距的衰减规律

图9(a)是实际记录的一组波形，不同地层电导率的响应基本上是重合的。在响应中，开始位置响应是突变的，即变化很快，到达极大值之后开始按照指数规律下降，下降的速度比较慢。将不同地层电导率的响应相减得到图9(b)，在475 ms位置，响应差有极小值，之后接着出现极大值，极大值与极小值的数值差别明显。图10是裸眼井的理论响应波形，其中，虚线是地层的电导率为0.05 S/m时0 m源距的响应波形，实线是电导率为0.05 S/m的响应减去电导率为2 S/m的响应差。虚线在瞬变激发位置(300 ms)的两边是对称的，相应地，实线在瞬变激发位置(300 ms)两边分别出现极小值和极大值。这些现象满足电磁感应原理：瞬变电磁激发的二次场是一次场对时间的导数。瞬变电磁测井响应(虚线)主要由一次场决定，响应差接近二次场。

图8 套管井响应最大值随源距的变化规律(理论计算)

图9(a)的瞬变电磁测井响应和图9(b)的响应差满足电磁感应原理。响应(主要是一次场)在突变位置不对称(开始一边快速变化，结束一边按照指数规律慢速变化)，相应地，其对时间的导数(响应相减以后得到的二次场)也是一边有极小值，绝对值比较大，一边有极大值，数值比较小。实验结果所展现出来的规律与理论计算结果相吻合。但是，理论与实验之间的差异也很明显。该差异主要来自实验电路本身。图11是考虑了激发波形的衰减过程以后的响应波形。图中用指数函数e-pt模拟瞬变激发的衰减过程，p值的不同代表衰减系数的不同。从图可以看到：p=0.4的响应基本上是两边对称的，p=0.04的响应开始出现不对称，p=0.01的响应的不对称加剧，p=0.004的响应已经完全不对称。图9(a)的响应形状与p=0.01的响应相似。注意：为了对比激发波形的衰减过程，图11中有四个瞬变激发位置(0 ms，300 ms，900 ms和1 200 ms)，我们仅仅将300 ms和1 200 ms位置的瞬变激发增加了指数衰减过程，其它两个位置没有考虑激发波形的衰减过程，因此，在0 ms位置，四种衰减系数的响应是重合的，在900 ms位置，除了p=0.04的响应受没有归零的影响外，其它响应线基本上是重合的。

图9 裸眼模型井(有机玻璃模型井)实验结果

图10 裸眼井的理论响应波形 图11 考虑激发波形衰减的响应波形

图12是套管模型井的瞬变电磁响应实验波形。同样，不同地层电导率的响应曲线完全重合，根本看不出其差别。将不同地层电导率的响应相减得到图中的两条线，由于响应差的幅度很小，其中干扰比较严重，毛刺比较多。我们从响应差的总体趋势看，其特征与图13的理论计算结果是一致的。图13中虚线为源距为0 m(左,虚线除以109)，地层电导率为1 S/m的响应，实线为虚线所示响应减去地层电导率为10 S/m的响应差。首先，理论计算结果的二次场(实线)在响应(虚线)的后面(右边)只有一个峰，在虚线的前面(左边)没有负峰。实验结果是：在响应突变位置0 ms处，响应差没有明显的负峰，在之后的指数衰减过程中，p=0.04的响应曲线(浅灰小毛刺)和p=0.01的响应曲线(深灰大毛刺)出现一个峰，位于响应(黑实线)峰的后面，这些现象与理论结果吻合。

图12 套管模型井的瞬变激发实验波形 图13 套管模型井的理论响应波形

5 结 论

通过实验，我们对瞬变电磁测井的理论响应波形有了一个更加全面的认识：瞬变电磁测井响应满足电磁感应原理，二次场是一次场对时间的导数。二次场响应的幅度比较小，套管井的二次场响应幅度更小。在理论响应波形中，如果不考虑电路对响应的影响，裸眼井的二次场响应在突变位置两侧有正、负两个峰，而套管井因为套管的屏蔽，只有后面(右侧)的一个峰。实验结果证实了上述结论：裸眼井有正负两个峰，套管井只有一个峰。但同时展现了电路对响应的重要影响：发射线圈内的电流关断前、后瞬变电磁响应严重不对称。这样，实验测量到的二次场响应的正、负两个峰的幅度和宽度均差异比较大。电路关断瞬间，电流突变，发射线圈上感应电压很高，激发出瞬变电磁场，向地层辐射瞬变电能量。关断完成后，线圈中储存的电能量通过电阻回路放电(放电过程与发射线圈的电路参数有关)，因为放电过程比较慢，其对应的二次场幅度很小。

在计算理论响应时，通常不考虑该放电过程所得到的结论是比较理想的，主要刻画瞬变电磁响应的物理过程。实验时，因为电路的时间常数受多种因素影响，而且每种影响因素之间又相互制约，不能够达到理想的情况，所以，其响应会在客观反映物理过程的同时，还表现出电路参数的影响。

[1] 张庚骥.电法测井[M].北京:石油工业出版社,1984.

[2] 戈 革,谢振全.宏观电磁场论[M].北京:石油工业出版社，1980.

[3] [英]I.S.Grant W.R.Phillips.刘岐元,王鸣阳,译.电磁学[M].北京:人民教育出版社,1982.

[4] [苏] J.A.别索诺夫.陈伟鑫,沈丽英,译.电工理论基础(下册)——非线性电路与电磁场[M].北京:高等教育出版社,1986.

石油管材专标委拟举办石油管重点技术标准宣贯会

为加大标准宣贯和实施的力度，帮助用户更准确地理解和使用标准，石油管材专标委计划于2015年5月28～29日在苏州举办非金属及复合管重点技术标准宣贯会和油井管重点技术标准宣贯会，分别对非金属及复合管专业6项标准和油井管专业8项标准进行宣贯，届时还将进行相关的专题讲座。欢迎从事石油管科研、生产、采购、检验、使用、管理和维护等工作的单位和个人踊跃参加。

会议详细内容及安排请访问http://tgrc.cnpc.com.cn/或拨打石油管材专标委秘书处电话：029-81887782、81887847，联系人：方伟、徐婷。

The Experimental Study on Transient Electromagnetic Logging

ZANG Defu1ZHANG Fuming1MAO Tong2SHEN Jianguo3

(1.LoggingCompanyofShengliPetroleumEngineeringCo.LTD.,Sinopec,Dongying,Shandong257096,China;2.CNPCGreatwallDrillingCompany,Beijing100101,China；3.PowerSonicLabofTianjinUniversity,Tianjin300072,China)

This paper presents experimental verification of transient electromagnetic logging principles.We use a plexiglass tube with an outside diameter of 113mm, wall thickness of 6mm, length 1m to simulates openhole borehole, and a plexiglass tube with an outside diameter of 350mm, wall thickness of 10mm thick to simulate formation, and use a one meter long of 5.5 inches casing pipe to simulate cased well.Homemade transmitter and receiver coils are motivated by a spacing of 150ms square wave.While measuring the received waveform of various source , the transient electromagnetic response attenuation law with source distance is accessed.Changing brine resistivity and measuring again with the response subtract of different formation resistivities offseting the first response field stimulated by transient electromagnetic, and obtain the secondary field response waveform which is a direct reflection of formation resistivity.It was found that: secondary field response waveform characteristics consistent with theoretical calculations and experimental results that borehole secondary field in the transient excited sides (on-off front and rear) both have extreme values, but opposite in sign; only one side of the cased well secondary field has extreme value.However, due to the decay constant of excitation circuit, the secondary field waveform magnitude is actually measured large in the current mutation side and small in exponentially decaying side.Borehole’s secondary field amplitude is much larger than the cased well’s secondary field amplitude.The original signal is small in measuring cased well formation resistivity.

transient electromagnetic logging, experiment, model well, secondary field, attenuation law

臧德福，男，1968年生，高级工程师，1989年毕业于西北大学理论物理专业，现在中石化胜利石油工程有限公司测井公司工作。E-mail:shenjianguo@tju.edu.cn

P631.8+11

A

2096-0077(2015)02-0021-05

2015-01-21 编辑：屈忆欣)