基于电路仿真的桥丝式电火工品静电危害预测

于鸿源,严 楠,陈树肖,王洪波

(1.石家庄陆军指挥学院军事运筹研究中心,河北 石家庄 050084; 2.北京理工大学爆炸科学与技术国家重点实验室,北京 100081)

1 引 言

人体静电是导致电火工品意外发火的重要危险激励源,由人体静电导致电火工品发生重大事故的事件已屡见不鲜[1-2]。静电导致电火工品爆炸的发火模式主要有脚脚间放电和脚壳间放电两种模式。当静电泄放的电能超过电火工品脚脚间通路的临界发火能量或发火件材料三态(固、液、气)转变阈值能量时,电火工品将发生爆炸或损伤。

穆丽君[3]、郭晓荣[4]、王鹏[5]等用数值计算和实验的方法分析了静电放电对电火工品伤害的机理,但通过电路仿真的方法分析静电放电对电火工品作用机理的相关研究在国内较少。国外在仿真和实验条件下模拟静电泄放源的主要方法是建立静电泄放等效电路模型[6-8],电路模型模拟包括人体电容、人体电阻、人体电感、敏感元件等效电阻和电击穿特性等参数,可从理论上揭示静电能量、静电电压、放电电流与放电回路参数的关系,但是用电路仿真的方法分析静电放电对电火工品的损伤机理,都没有设置多组仿真电压以便更全面地讨论静电泄放条件及电路模型参数对电火工品的危害。

本研究对10,20,25,30,40,50 kV共6组泄放初始电压的静电泄放响应特性进行仿真和分析,研究静电泄放条件对电火工品危害作用的基本规律,分析静电泄放电压和电路参数对于泄放电流的影响; 同时进一步计算静电泄放模型释放出的能量,选取典型的桥丝式火工品发火件设计参数,通过计算静电放电能量与发火件材料三态临界特征值、发火特性的关系,揭示静电危害机理和危害特性,从而预测不同静电条件对电火工品的危害程度。

2 静电泄放电路模型建立和电路参数选取

静电泄放模型电路可以模拟静电泄放时产生的电流、能量及作用效果。国内外的相关研究中[9-12]主要包括两种人体静电泄放模型电路,一种是单RC静电泄放模型电路,另一种是双RC静电泄放模型电路。双RC类型模型在静电泄放模拟过程中分配到电火工品上的峰值电流和放电能量较单RC模型更大[9-12],因此本研究的仿真和计算选取了双RC类型模型电路。

2.1 双RC人体静电模型电路特点分析

被广泛采用的双RC人体静电泄放模型电路有美国Sandia实验室发布的模型和美国电气和电子工程师协会(IEEE)发布的模型[6-8],这两种模型电路通常用于较严酷静电环境的模拟,能够覆盖电火工品使用过程中最严酷的静电环境。本研究的仿真和计算分别选取了这两种模型。

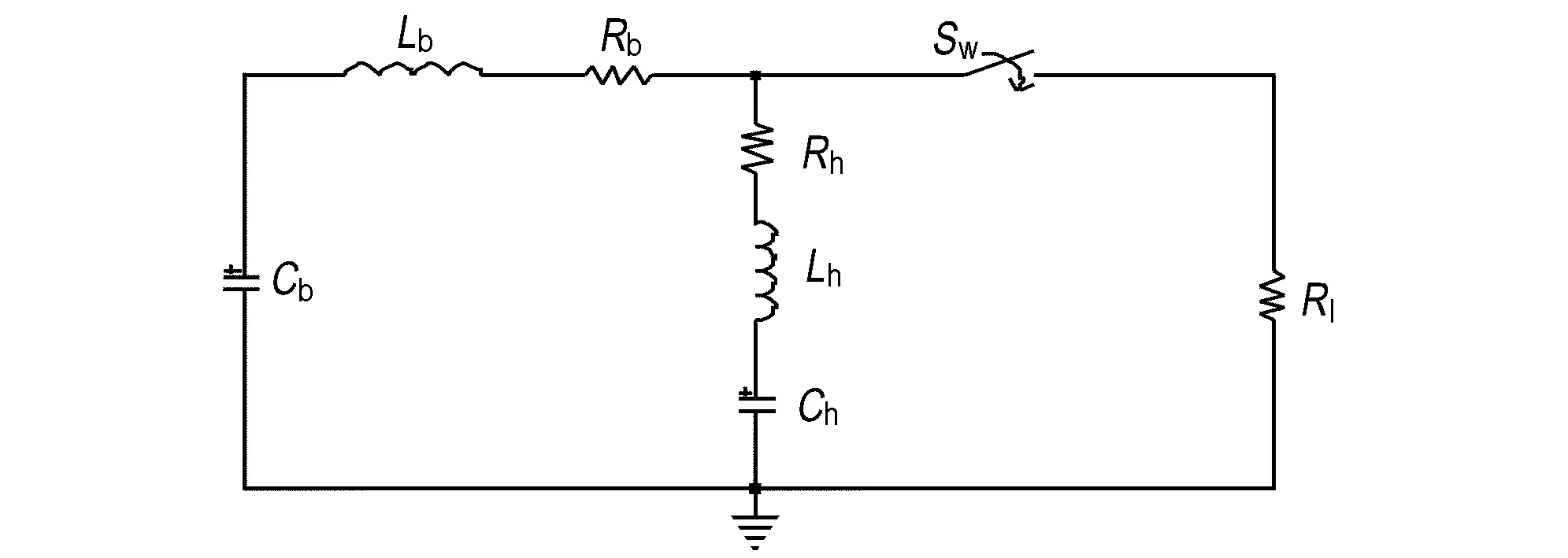
两种静电泄放模型电路分别如图1a[11]和图1b[12]所示。由图1a和图1b可见,两种静电泄放模型电路均由两个回路组成,一部分模拟人手指的快速放电,另一部分模拟人体的慢速放电,代表人体放电的第一个回路由电容Cb、电阻Rb、电感Lb组成,代表人体手指放电的第二个回路由电容Ch、电阻Rh、电感Lh组成,Sw用于模拟静电泄放开关,R1表示的是泄放对象等效电阻,即模拟实际应用中电火工品桥丝电阻。两种模型电路在结构上的差异仅在于代表人手的阻抗元件在电路结构中的位置不同。

两种电路模型的元件参数值见表1。由表1可见,Sandia实验室标准的静电泄放电路模型参考了前人大量的研究测试数据,以提供最大峰值电流并将最多的能量传送给受害物为准则,确定了电路模型的元件参数值,IEEE电路模型没有为电路元件指定确定的参数,而是为其提供了参考取值范围,供使用者选用。

a.ESD for Sandia lab standard[11]

b.ESD for IEEE standard[12]

图1 Sandia实验室标准和IEEE标准双RC人体静电放电等效模型
Fig.1 Double RC equivalent model of human body electrostatic discharge for Sandia lab standard and IEEE standard

表1 电路模型的元件参数取值范围[11-12]Table 1 The range of element parameter values defined in the circuit model [11-12]

2.2 仿真研究方案的设计

在Sandia实验室报告中[6],叙述了对2.1节中的两种模型在25 kV初始电压下的静电泄放仿真,但其仿真所使用的受害敏感元件是阻值为10 mΩ级的铂金属桥丝,与国内的桥丝式电火工品中常用的镍铬桥丝阻值相差较大[13],因此本研究仿真选取了阻值为2.8 Ω的典型镍铬桥丝换能元件作为静电泄放敏感元件。并且在仿真计算中将10～50 kV的一系列电压值作为静电泄放初始电压,以分析电路模型的放电规律。

两种等效电路模型在仿真时选取的参数见表2。电路模型各元件参数的选取原则是基于在仿真过程中获得最严酷的情形,因此仿真电路的能量存储元件选择取值范围中的最高值,阻抗元件选择取值范围中的最低值,以获得最大的放电电流和放电能量。

表2 仿真选取的电路元件参数值[11-13]Table 2 The parameter values of circuit element selected in the simulation[11-13]

研究采用PSpice电路仿真软件[14]搭建静电模型电路、仿真静电泄放结果、查看静电泄放电流值和电压值,并对仿真得到的电流值、电压值进行数学运算处理。该软件是以计算机辅助设计为基础的电子设计自动化技术软件,是目前电路设计和仿真中常用的软件[14]。

根据IEEE相关标准的定义[15],静电危害特性的分析主要针对峰值电流,即电流波形的最大值,记为Imax; 脉冲上升时间,电流脉冲从峰值的10%上升到90%所用的时间,记为tr; 脉冲衰减时间,电流脉冲从峰值下降到峰值的36.8%所用的时间,记为td。分析结果与Sandia实验室报告[11]及IEEE标准[12]对比可以验证仿真程序和计算过程的正确性,而后选取多组静电高压条件仿真分析,总结发火材料对静电高压的响应规律。

3 静电泄放电路模型仿真分析

3.1 仿真正确性的验证

根据国军标[9]的相关要求,首先选择25 kV的电压作为静电泄放仿真的初始泄放电压,此时根据式(1)中的电容储能公式计算可知,Sandia模型泄放电容的储能值为128.12 mJ,IEEE模型泄放电容中的储能值约96.88 mJ。

(1)

式中,W为电容储能,J;C为电容量,F;U为电容两极间电势差,V。

使用PSpice软件[14]按照2.1节中的电路模型结构和2.2节中选取的元件参数搭建如图1a和图1b的电路模型,设定放电开关Sw在0 s时闭合,仿真程序计算并输出的仿真结果如图2。将图2中的仿真波形结果与Sandia实验室报告[11]及IEEE标准[12]公布的人体静电泄放波形及参数比对可知,结果与标准描述完全符合,从而印证了本仿真程序和计算过程的正确性。

图2 25 kV静电电压条件下仿真的泄放电流波形
Fig.2 The computational current profile of ESD model at 25 kV

3.2 静电泄放响应规律分析

在确认仿真程序计算结果正确的前提下,本研究选择了10,20,30,40,50 kV不同静电高压条件分别对两种人体静电模型进行仿真分析,结果如图3和图4所示。由图3和图4可见,在相同静电电压条件下,IEEE模型仿真的峰值电流大大高于Sandia模型的峰值电流,其脉冲上升时间较Sandia模型的参数略小,其脉冲衰减时间显著小于Sandia模型的参数,脉冲电流衰减快,电流作用时间较短,即Sandia模型的泄放电流作用时间较长。

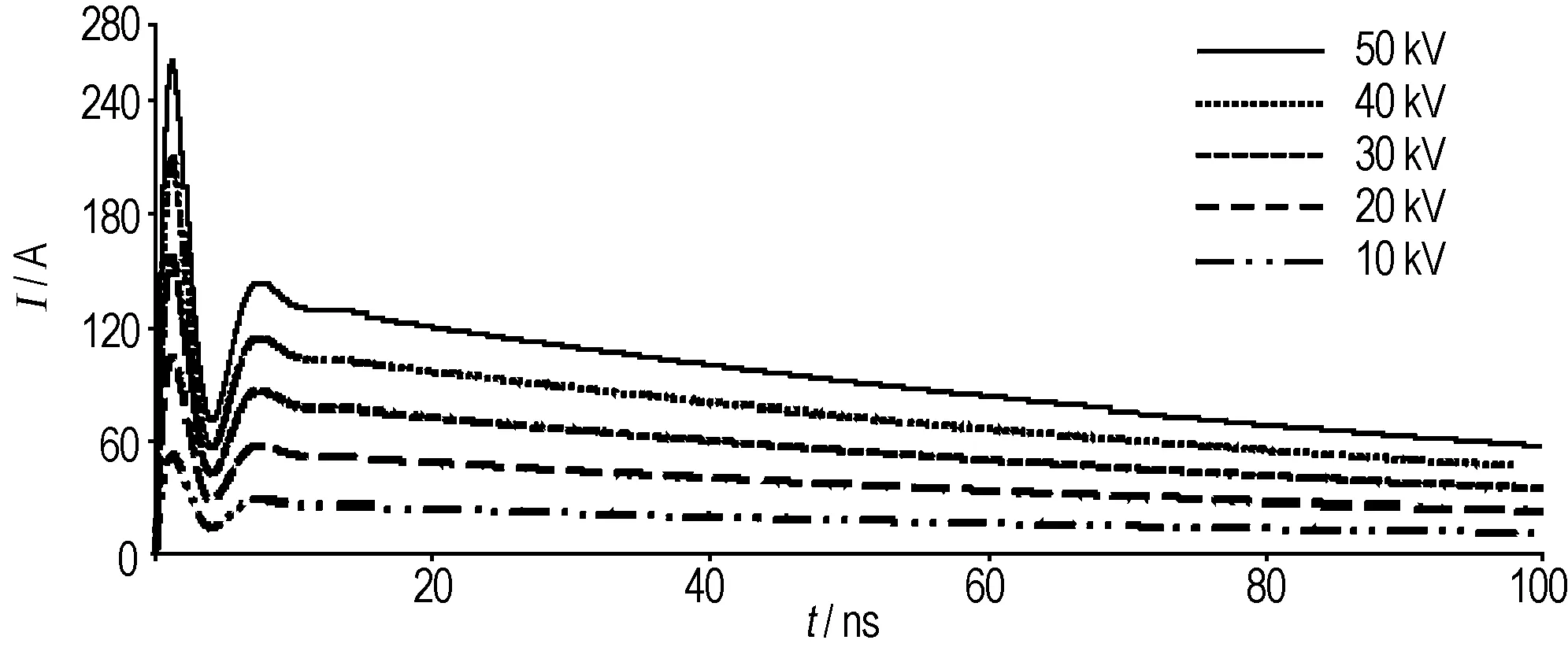
图3 Sandia模型在不同静电电压条件下泄放电流仿真波形
Fig.3 The computational current profile of Sandia ESD model under different electrostatic voltage condition

图4 IEEE模型在不同静电电压条件下泄放电流仿真波形
Fig.4 The computational current profile of IEEE ESD model under different electrostatic voltage condition

根据图3和图4的仿真波形和数据,进一步整理仿真结果列于表3。由表3可见,对于同一种静电泄放模型,改变其泄放的初始静电电压值,其静电泄放电流的峰值也随之改变,且电流峰值与初始电压值成正比例关系变化,而泄放电流的脉冲上升时间与脉冲衰减时间并不随电压初值改变而改变。由此可见,泄放电流的脉冲上升时间与脉冲衰减时间两项参数只与模型电路的固有电路参数有关。

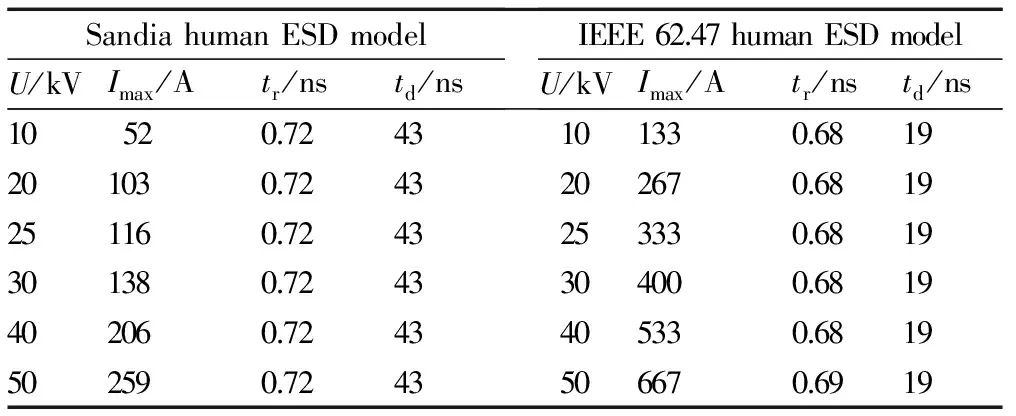
表3 仿真得到的泄放电流的波形参数Table 3 The profile parameters of discharge current obtained by simulation

Note:tris rise time of discharge current,tdis delay time of discharge current.

4 静电泄放对火工品危害特性的分析

4.1 电火工品典型临界能量特性分析

电火工品的发火件材料组成包括桥丝、焊锡、起爆药、脚线、电极塞基体材料等。静电放电导致电火工品的损伤条件可以用桥丝电热升温达到的典型临界能量特性作为判据,如药剂发火点、桥丝熔断温度等,如果升温达到起爆药的爆发点,即可视为发生了爆炸。

常见的桥丝式电火工品的桥丝材料为镍铬合金(6J20)[13],此材料的熔点约为1400 ℃; 焊锡的熔点约为183 ℃; 电火工品内部的常用起爆药剂有叠氮化铅或斯蒂芬酸铅,叠氮化铅的热分解温度为260 ℃,爆发点为282 ℃; 斯蒂芬酸铅的热分解温度为245 ℃,爆发点为327 ℃[16]。电火工品内部温度达到上述温度,其内部材料将受到不同程度的损伤,火工品的性能即可能遭到破坏。比如达到药剂的熔点温度会导致药剂熔化变质,达到分解温度时会发生药剂分解变质,达到爆发点会发生爆炸; 达到桥丝的熔点温度,桥丝会发生扭曲、截面面积变化或熔断。即当达到不同的阈值温度时,则达到相应程度的损伤。

静电泄放电流通过电火工品的脚线传导到电火工品内部的桥丝上,通过桥丝电热作用进而对电火工品桥丝和药剂产生危害作用。本研究把静电泄放对电火工品的危害用作用积分(Action Integral)参量来定量表示,记作Z。作用积分定义为作用电流的平方值在作用时间上的积分,单位是A2·s,其优点是可以表示单位电阻上静电作用的能量值,因而具有普遍适用性,对应的其它电阻值的能量仅需乘上电阻值即可得到。桥丝上的电流作用积分会导致桥丝温度升高,由于静电泄放时间极短,一般在几十纳秒之内,如此快的静电放电和桥丝升温过程,可以忽略桥丝热损失,因此可以断定初始温升阶段,桥丝的电热升温速率远远大于药剂的化学放热速率,所以这一阶段化学放热可以忽略不计,系统的温度由桥丝的电热放热速率决定[5],电火工品内部的温度升高值与桥丝上的作用积分服从关系式(2)[6]。

(2)

(3)

本文为系统温升计算选择了一种典型的镍铬桥丝,其参数见表4。其中d表示桥丝直径,m;R表示电阻值,Ω。

表4 计算所用的典型电火工品参数[13]Table 4 The parameter values used for calculation of typical EED [13]

将本节中火工品损伤的阈值温度(T)点及表4中的参数值带入到关系式(3)中计算,得到电火工品内部达到各阈值温度点时发挥电热作用的镍铬桥丝上需要的作用积分值(Z),其结果见表5。由表5可见,达到镍铬桥丝材料的熔点时需要作用积分值为1.51×10-3A2·s; 达到焊锡材料的熔点时需要作用积分值为2.07×10-4A2·s; 达到叠氮化铅药剂的分解点需要作用积分值为3.01×10-4A2·s,到达爆发点需要作用积分值为3.28×10-4A2·s; 达到斯蒂芬酸铅药剂的分解点需要作用积分值为2.83×10-4A2·s,到达爆发点需要作用积分值为3.82×10-4A2·s。根据本节叙述,静电作用的作用积分达到表5中各材料对应的作用积分临界值时,就会使电火工品内部的温度达到火工品损伤的阈值温度,电火工品内部的结构和材料特性将遭到破坏。

表5 发火材料温度阈值与作用积分阈值的对应关系Table 5 Corresponding relation of temperature threshold of firing materials and action integral threshold

Note:Tis temperature threshold of firing materials,Zis action integral threshold.

4.2 静电泄放能量特性及对电火工品的危害预测

根据4.1节对于电流作用积分的定义,利用PSpice仿真软件对3.2节中的泄放电流结果做平方运算并在时间上积分,得到如表6所示的不同泄放模型在不同静电电压条件下的电流作用积分值。对比表5与表6中的数据可得,在国军标[9]规定的25 kV静电条件下,无论按照Sandia人体静电泄放模型还是IEEE人体静电泄放模型,静电泄放直接作用于电火工品的桥丝时(不考虑热量散失),都可导致火工品内的焊锡熔化,内部的斯蒂芬酸铅或叠氮化铅药剂达到分解点和爆发点,但是不足以使镍铬桥丝熔化。

使用Sandia模型模拟的情况下,20 kV时可导致火工品内部的焊锡熔化,电压达到50 kV时,可接近镍铬桥丝熔点。使用IEEE模型仿真的情形较Sandia模型更为严酷,但是10 kV的静电泄放电压仍然不足以使焊锡熔化,20 kV时就可以到达药剂的分解点和爆发点,40 kV的电压可导致桥丝熔化。

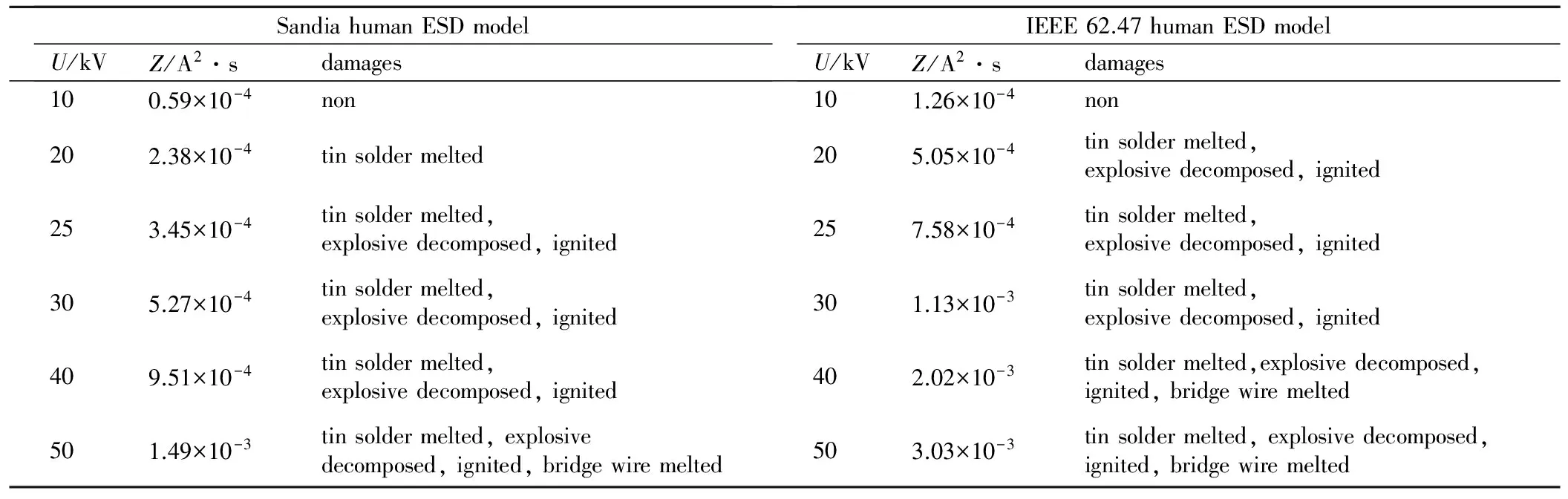
表6 泄放模型的作用积分值Table 6 The calculated action integral values of different discharge models

5 结 论

(1)针对桥丝式电火工品对于静电放电的响应规律研究,选取了10～50 kV的静电放电条件,在PSpice软件中分别建立Sandia实验室标准静电模型电路和IEEE标准静电模型电路对40 μm直径的镍铬材料桥丝做静电放电仿真。结果表明静电放电电流的峰值随着初始电压而成比例增加,而脉冲上升时间和脉冲衰减时间是电路的固有属性,不随初始电压的变化而改变。在相同的初始电压条件下,IEEE模型的泄放电流峰值较大,响应速度较快。

(2)在电路仿真结果理论计算的基础上对静电放电对于桥丝式电火工品发火材料的危害进行了预测。在最为严酷并且不考虑热量散失的情形中,25 kV的放电情况下电火工品内部温度会达到焊锡和药剂的损伤阈值能量,不会达到桥丝熔点值; IEEE模型在40 kV时可导致桥丝熔化,而Sandia模型要达到50 kV。这个结果有效地反映了高压静电环境对桥丝式电火工品的危害作用,预测出静电放电条件下电火工品内部产生的变化,为电火工品的静电防护提供了理论依据和参考。

参考文献:

[1] 李志敏,张同来,杨利,等.火炸药静电性能研究进展[J].科技导报,2011,29(26):74-79.

LI Zhi-min,ZHANG Tong-lai,YANG Li,et al.Progress on electrostatic performances of explosive[J].Science&TechnologyReview,2011,29(26):74-79.

[2] 刘尚合,宋学君.静电及其研究进展[J].自然杂志,2007,29(2):63-69.

LIU Shang-he,SONG Xue-jun.Progress in electrostatic and related research[J].ChineseJournalofNature,2007,29(2):63-68.

[3] 穆丽君,高俊国,张玉令.静电放电对电火工品作用机理研究分析与试验研究[J].工业安全与环保,2010,36(5):39-40.

MU Li-jun,GAO Jun-guo,ZHANG Yu-ling.Effect mechanism analysis and test investigation of electrostatic stimulus on electric explosive devices[J].IndustrialSafetyandEnvironmentalProtection,2010,36(5):39-40.

[4] 郭晓荣,朱顺官,张琳,等.半导体桥静电作用前后点火特性[J].含能材料,2012,20(1):99-104.

GUO Xiao-rong,ZHU Shun-guan,ZHANG Lin,et al.Ignition characteristics of non-electrostatic discharge and electrostatic discharge on semiconductor bridge[J].ChineseJournalofEnergetic

Materials(HannengCailiao),2012,20(1):99-104.

[5] 王鹏,杜志明.桥丝式电火工品热点火理论[J].火工品,2007(4):26-30.

WANG Peng,DU Zhi-ming.Thermal ignition theory of electric hot wire initiating devices[J]．Initiators&Pyrotechnics,2007(4):26-30.

[6] Wilson M J.Projected response of typical detonators to electrostatic discharge (ESD) environments[R].UCRL-ID-145642,2002.

[7] Tsuyoshi Takada,Tadatoshi Sekine,Hideki Asai.Hybrid simulation of ESD events by SPICE-like and finite-difference time-domain methods[C]∥2013 IEEE Electrical Design of Advanced Packaging & Systems Symposium (EDAPS),2013,Nara,Japan.197-200.

[8]MengKuo-hsuan,Rosenbaum Elyse.Verification of snapback model by transient I-V measurement for circuit simulation of ESD response[J].IEEETransactionsOnDeviceandMaterialsReliability,2013,13(2):371-378.

[9] 国防科学技术工业委员会.GJB 5309.14-2004.火工品试验方法第14部分:静电放电试验[S].2004.

Commission of Science Technology and Industry for National Defense.GJB 5309.14-2004.Test methods of initiating explosive devices-Part 14:Electrostatic discharge test[S].2004.

[10] United States Department of Defense.MIL-STD-331C.Department of defense test method standard:Fuze and fuze components,environmental and performance tests for[S].2005.

[11] Bruce Berry R.Electrostatic discharge testing of propellants and primers[R].SAND-92-2416·UC-742,1992.

[12] American National Standards Institute.IEEE Std 62.47-1992.IEEE guide on electrostatic discharge (ESD):Characterization of the ESD environment [S].1992.

[13] 蔡瑞娇.火工品设计原理[M].北京:北京理工大学出版社,1999:227-229.

CAI Rui-jiao.Initiators and pypotechnics designing theory.Beijing:Beijing Insititude of Technology Press,1999:227-229.

[14] 张正茂,胡心.基于PSpice的光电探测电路仿真分析[J].光电技术应用,2012,27(5):69-76.

ZHANG Zheng-mao,HU Xin.Simulation and analysis of electro-optical detection circuit based on PSpice[J].Electro-opticTechnologyApplication,2012,27(5):69-76.

[15] IEEE Standards Board.IEEE Std C62.38-1994.IEEE guide on electrostatic discharge (ESD):ESD withstand capability evaluation methods (for Electronic Equipment Subassemblies) [S].1994.

[16] 劳允亮.起爆药化学与工艺学[M].北京:北京理工大学出版社,2004:232-238.

LAO Yun-liao.Chemistry and technology of primary explosive[M].Beijing:Beijing Insititude of Technology Press,2004:232-238.