砾岩地层电阻率与孔隙度和孔隙形状关系数值模拟
2015-05-10解茜草孙超仵杰
解茜草, 孙超, 仵杰
(1.西北工业大学, 陕西 西安 710072; 2.西安石油大学光电油气测井与检测教育部重点实验室, 陕西 西安 710065)
0 引 言
砾岩储层岩性复杂,电阻率测井响应受岩石骨架和孔隙结构影响严重,非均质性强,孔隙结构复杂[1]。为改善阿尔奇公式的应用效果,需要研究适应复杂孔隙结构储层特点的岩电参数选取办法[2-4]。Munish Kumar[5]给出了不同饱和度条件下电阻率响应特性;Herrick D C and Kennedy W D[6]研究了不同孔隙度时几种模型中的电流特性。刘堂晏等[7]应用球管模型研究了不同孔隙结构、不同流体饱和度时的岩石导电性,证明复杂孔隙结构是形成低电阻率油层的重要因素。Yue W Z等[8]采用LGA方法研究了2层导电媒质中地层因素与孔隙度之间的关系,根据模拟和实验数据开发了关于F-φ的新方程,改善了对孔隙结构的评价。David Kennedy[9]研究了将阿奇公式分别应用于电导率张量的各个分量计算含水饱和度。Li X Y等[10]研究了岩石胶结指数m的变化会导致用阿奇公式计算饱和度产生误差,利用Maxwell方程推导出计算复杂孔隙地层胶结指数m的计算模型。本文研究恒定电场中砾岩地层电阻率的三维数值计算,探究砾岩地层电阻率与孔隙度和孔隙形状的关系,分析各向异性砾岩地层岩性参数的确定方法,为砾岩油藏的评价和解释提供依据,扩展对各向异性的认识。

图1 均匀砾岩地层模型
1 理论与方法
1.1 恒定电流场中计算砾岩地层视电阻率
恒定电场中计算砾岩地层视电阻率
Ra=kΔUI
(1)
式中,k定义为电极系数。
砾岩地层模型两端加上电极,发射电极和回路电极之间电位差ΔU=1 V,测量回路电极上的电流值I即可计算出地层的视电阻率Ra。
恒定电场中电场及电流密度满足Maxwell方程
×E=0
(2)
J=σE
(3)
式中,σ为电导率,S/m;E为电场强度,V/m;J为电流密度,A/m2。
根据电流连续性定理,电流可由回路端的法向电流密度进行积分得到,即
I=∬sJn·dS
(4)
砾岩地层模型具有复杂孔隙结构,表现出电各向异性。分别在x、y、z的3个方向施加电极,式(4)中,n为x、y或z。
1.2 岩石电阻率与孔隙度的关系
岩石储集物性的好坏取决于岩石的有效孔隙度。孔隙中完全充满水的岩石电阻率R0与所含水的电阻率Rw、孔隙度φ及岩性有关,无论如何改变地层水电阻率Rw值,含水岩石的电阻率R0与所含地层水电阻率Rw的比值总是一个常数,即
R0Rw=F=aφ-m
(5)
F定义为岩石地层因素。这个比值只与岩样的孔隙度、胶结情况和孔隙形状有关,而与饱含在岩样孔隙中的地层水电阻率Rw无关;其中,a为与岩性有关的比例系数,m为岩石胶结指数。为了确定a与m的值,式(5)两边取对数
lgF=lga-mlgφ
(6)
式中的负号使得即使回归直线的斜率为负,m也能取正值。由式(6)可知,取2组(lgφ,lgF)就可以确定其线性关系,斜率为-m,截距为lga。
对于各向异性地层,此时,Rw、φ为标量,而o、、及为张量,o为实对称矩阵,将o进行矩阵变换为对角阵,利用矩阵对数和指数运算的概念,则、及均为对角阵,有
lg=lg-lgφ
(7)
1.3 数值模型
为模拟复杂砾岩地层,需要选择合适的砾岩颗粒形状。孔隙与砾岩颗粒之间网格的衔接和过渡至关重要,对网格的最大尺寸和最小尺寸进行限定,用增大率进行微调得到不同部分之间合理的网格过渡和衔接,2个砾岩颗粒之间的网格由密到疏,再由疏到密。图1(a)为颗粒大小相等的方形砾岩地层模型,其孔隙度可以任意调节。
本文采用方形砾岩数值模型,砾岩骨架等效为棱长为100 mm的立方体,砾岩电阻率4 Ω·m,砾岩颗粒之间无胶结。
图1(b)、(c)分别为发射电极和回路电极在同一方向和不同方向时地层中的电流分布。可见,电流从发射电极出发,大部分通过空隙中的流体,少部分穿过砾岩到达回路电极。
图3 模型1及其地层因素与孔隙度关系
2 砾岩地层电阻率与孔隙度和孔隙形状的关系
2.1 均匀砾岩地层中地层因素与孔隙度定量关系
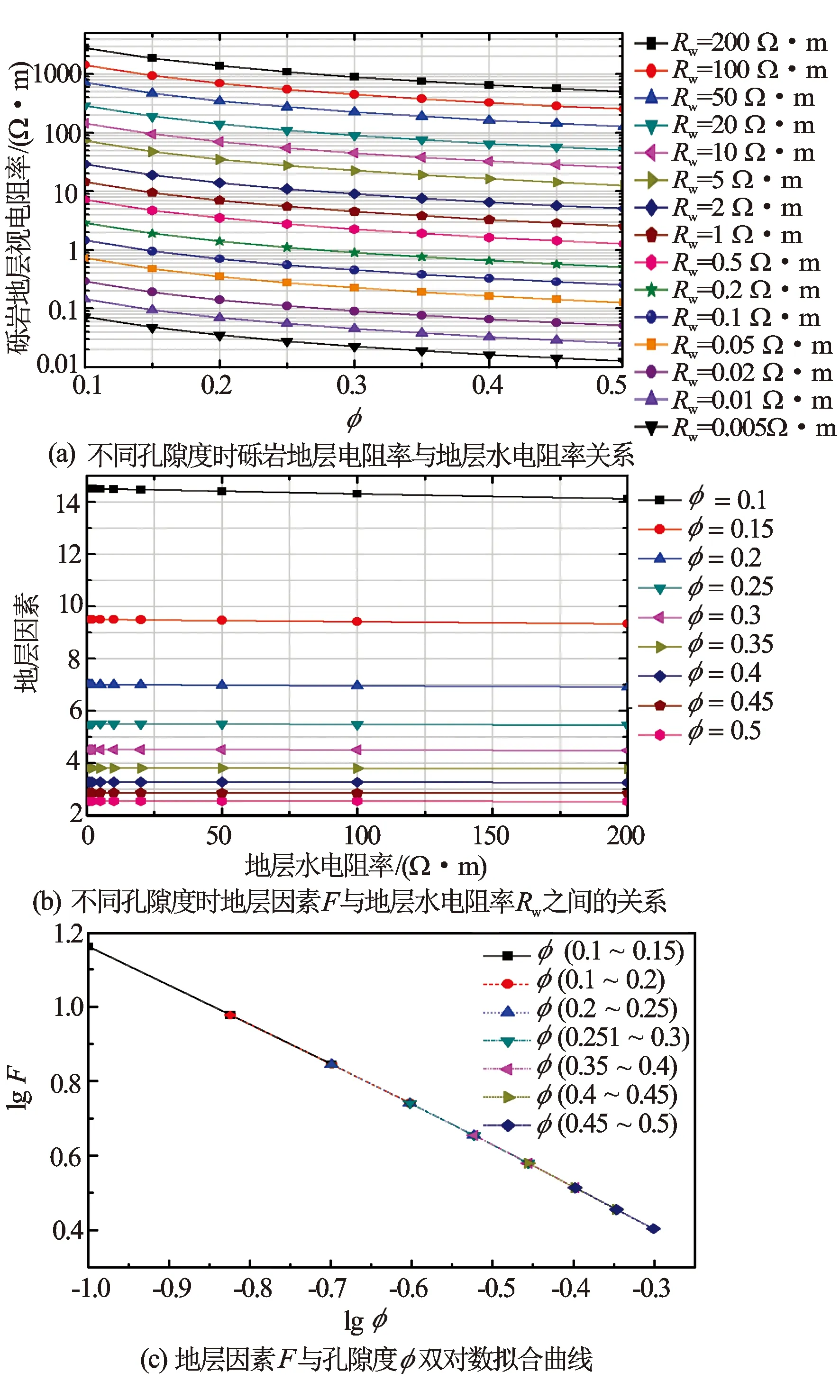
图2 均匀砾岩地层模型地层因素与孔隙度的定量关系
研究图1(a)中所示均匀砾岩地层模型,x、y、z3个方向上砾岩均为大小相同的小立方体砾岩颗粒,孔隙中充满水。图2(a)所示为不同孔隙度时砾岩地层电阻率与水电阻率的变化趋势,砾岩地层电阻率随水电阻率增大而线性增大;图2(b)所示为不同孔隙度时地层因素F与地层水电阻率之间的关系,与式(5)结论一致。大部分电流是从孔隙中穿过,当孔隙中水电阻率不变时砾岩地层电阻率主要受孔隙度的影响,孔隙度越小,电流越不容易通过,会有部分电流穿过砾岩到达回路电极,砾岩地层电阻率越大。图2(c)所示为地层因素F与孔隙度φ双对数拟合曲线。
2.2 几种各向异性砾岩地层模型中地层因素与孔隙度之间的定量关系
当3个方向上砾岩个数不相同或砾岩排列不同时即可模拟各向异性砾岩地层模型。
2.2.1 模型1
砾岩地层模型如图3(a)所示,偶数层砾岩整体向xy方向平移了50 mm,砾岩大小不变,x方向与y方向上砾岩排列一致,此时偶数层的每个砾岩间隔也随着移动改变而与奇数层砾岩间隔不同,改变砾岩的大小,即可得到不同孔隙度下的砾岩地层电阻率。根据模型特征,有
lgFyy=lgFxx=lgaxx-mxxlgφ
lgFzz=lgazz-mzzlgφ
(8)
模型1地层因素与孔隙度关系如图3(d)、表1所示;与图2(c)比较后可知,当偶数层砾岩整体平移后,孔隙的迂曲程度发生了变化,电流不再很顺利地从直的孔隙中穿过,一部分电流穿过砾岩,因此砾岩地层电阻率增大。
2.2.2 模型2
砾岩地层模型如图4(a)所示。偶数层砾岩整体向x方向平移了50 mm,为了保持在移动的过程中砾岩大小不变,偶数层x方向上每个砾岩间隔也随着移动有所改变,与y方向上砾岩间隔与奇数层砾岩间隔一致。模型中,砾岩在x、y、z的3个方向上排列均不同,有
表1 不同孔隙度范围内与的3个主轴分量

表1 不同孔隙度范围内与的3个主轴分量
孔隙度^a的3个主轴分量^m的3个主轴分量ϕ=01~015axx=01875,ayy=01875,azz=01611mxx=10214,myy=10214,mzz=10227ϕ=015~02axx=01256,ayy=01256,azz=01397mxx=09604,myy=09604,mzz=10405ϕ=02~025axx=0107,ayy=0107,azz=00911mxx=1104,myy=1104,mzz=09399ϕ=025~03axx=00822,ayy=00822,azz=0095mxx=1029,myy=1029,mzz=1038ϕ=03~035axx=0069,ayy=0069,azz=0075mxx=10307,myy=10307,mzz=11203ϕ=035~04axx=00521,ayy=00521,azz=00519mxx=089894,myy=089894,mzz=0895ϕ=04~045axx=00533,ayy=00533,azz=008mxx=1042,myy=1042,mzz=1564ϕ=045~05axx=00431,ayy=00431,azz=00701mxx=09419,myy=09419,mzz=1532
lgFxx=lgaxx-mxxlgφ
lgFyy=lgayy-myylgφ
lgFzz=lgazz-mzzlgφ
(9)
地层因素F与孔隙度关系如图4(d)所示。可见当孔隙度一定时,在不同方向上lgF的值各不相同,lgFxx与lgFyy值很接近。这是因为砾岩地层的偶数层是整体沿着x方向移动的,x方向和y方向的孔隙迂曲情况并没有发生很大的变化,所以,当发射电极和接收电极都位于x方向或都位于y方向时,lgFxx与lgFyy值便很接近。
2.2.3 模型3
砾岩地层模型如图5(a)所示。偶数层的砾岩的偶数排不变,奇数排沿x方向移动50 mm,为了保持在移动的过程中砾岩大小不变,偶数排x方向上的每个砾岩间隔也随着移动有所改变,且偶数层奇数排和y方向上砾岩的间隔与奇数层的砾岩间隔一致。此模型中,砾岩在x、y、z的3个方向上的排列均不同,地层因素与孔隙度的双对数公式同模型2相同。
模型3地层因素与孔隙度关系如图5(d)所示。可见当孔隙度一定时,在不同方向上lgF的值各不相同,当孔隙度一定时,在不同方向上lgF的值比较接近但各不相同,lgFxx的值稍小些。通过模型3砾岩的排列情况,可以看出y方向和z方向上孔隙迂曲程度很接近,所以电流从发射电极流向接收电极的情况近似,故所得值较为接近;而x方向相孔隙较好,电流容易流过,在此方向上砾岩地层电阻率的值较小,地层因素也相对小一些。
2.2.4 长方体砾岩各向异性地层模型
选用长方体砾岩组成各向异性砾岩地层模型,x方向上4个砾岩,y和z方向上5个砾岩,x方向上砾岩的棱长大于y方向与z方向的棱长[见图6(a)]。在该模型中y方向与z方向的排列方式一致,因此

图4 模型2及其地层因素与孔隙度关系

图5 模型3及其地层因素与孔隙度关系
lgFyy=lgFzz=lgazz-mzzlgφ
lgFxx=lgaxx-mxxlgφ
(10)
模型4地层因素与孔隙度关系如图6(b)所示。当采用长方体砾岩构造各向异性砾岩地层时,lgFzz与lgFxx的值在孔隙度较小时差距相对较大,而在孔隙度较大时差距很小。那是因为在孔隙较小时,x方向上砾岩比z方向上的排列较为紧密,通过孔隙到达回路电极的电流较少,因此砾岩地层电阻率就较大,地层因数F值也较大;而当孔隙度增大时,电流比较容易通过孔隙到达回路电极,所以随着孔隙度的增大lgFzz与lgFxx的差也逐渐减小。同理可解释lgFzx与lgFxy值的变化情况。
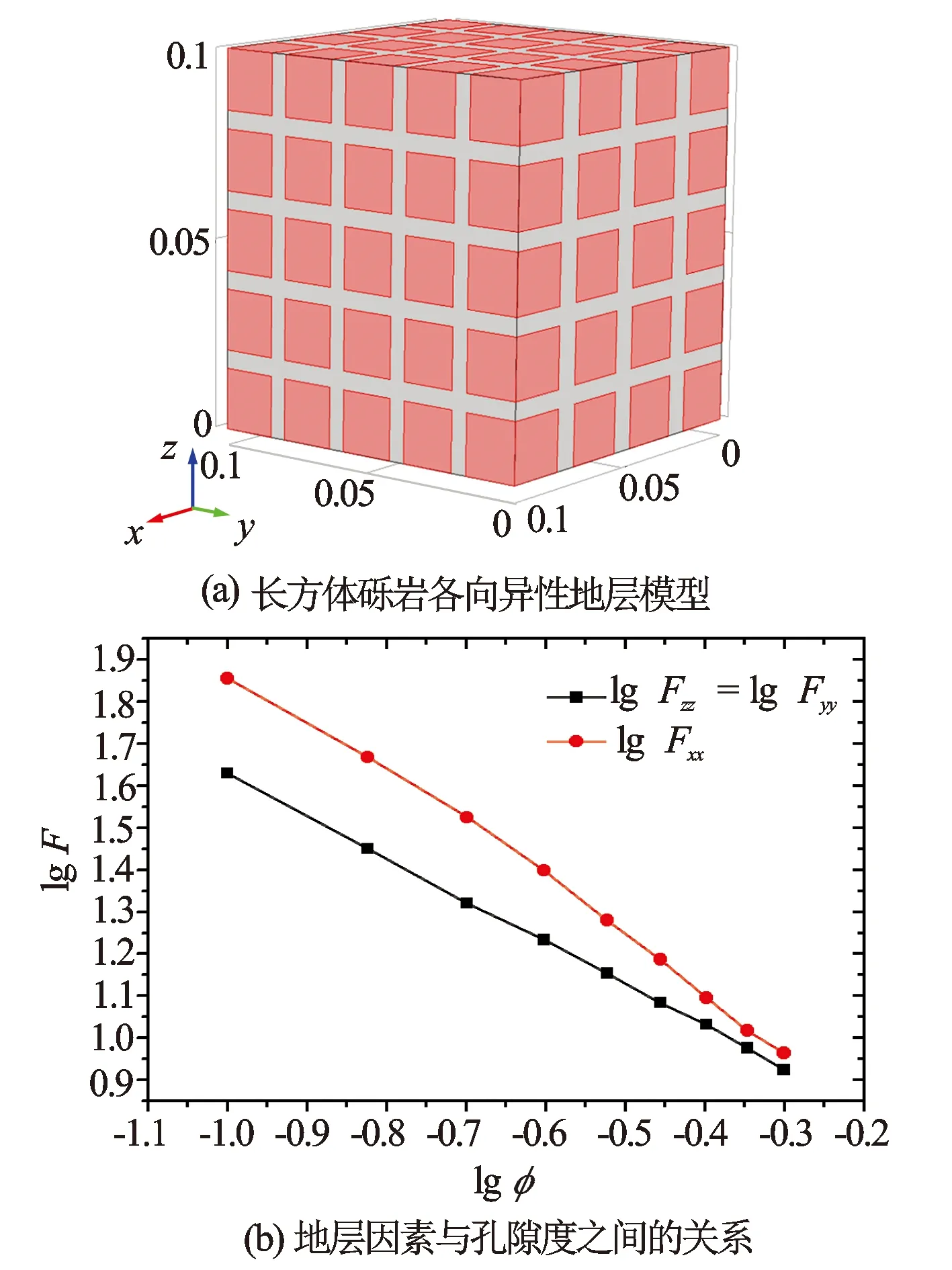
图6 长方体各向异性砾岩地层模型及其地层因素与孔隙度的关系
本文研究了砾岩颗粒无胶结的方形砾岩地层模型中孔隙的变化,若考虑孔喉配位数的变化,最好采用球形或椭球形砾岩颗粒模型。
3 结 论
(1) 建立各向异性砾岩地层模型,研究恒定电场中砾岩地层电阻率三维数值计算及复杂砾岩地层模型网格剖分方法,提高数值解的稳定性、可靠性。
(2) 数值计算分析砾岩地层中的电流分布,研究砾岩地层电阻率与孔隙度和孔隙形状的关系。岩石孔隙度越大,含地层水越多,岩石导电能力越强,则岩石电阻率就越小;反之,岩石孔隙度越小,则岩石电阻率就越大。岩石的孔隙形状决定了地层水的分布。孔隙形状越复杂,孔隙连通性越差,孔道弯曲程度越大,离子移动所受阻力也越大,则岩石电阻率就越高。
(3) 由地层因素F与孔隙度φ双对数拟合曲线可确定各向异性砾岩地层岩性参数,为砾岩油藏的评价和解释提供依据。
参考文献:
[1] 段雁超, 仵杰, 曹婷. 均匀地层中单个砾岩对阵列感应响应的影响机理分析 [J]. 西安石油大学学报, 2013, 28(5): 51-56.
[2] Carlos F Haro. The Equations Archie Forgot: Anisotropy of the Rocks [C]∥Reservoir & Engineering, 2010, SPE: 823-836.
[3] Carlos F Haro. Permeability Modeling in Porous Media: Setting Archie and Carman-Kozeny Right [C]∥Society of Petroleum Engineer Inc, 2007: 1-12.
[4] 陈锋, 安金珍, 廖椿庭. 原始电阻率各向异性岩石电阻率变化的方向性 [J]. 地球物理学报, 2003, 46(2): 271-280.
[5] Munish Kumar, Tim J Senden, Adrian P Sheppard, et al. Probing the Archie’s Exponent under Variable Saturation Conditions [J]. Petrophysics, 2011, 52(2): 124-134.
[6] Herrick D C, Kennedy W D. A New Look at Electrical Conduction in Porous Media: A Physical Description of Rock Conductivity [C]∥SPWLA 50th Annual Logging Symposium, 2009.
[7] 刘堂晏, 汤天知, 杜环虹, 等. 考虑储层孔隙结构的岩石导电机制研究 [J]. 地球物理学报, 2013, 56(8): 2818-2826.
[8] Wenzheng Y, Tao G, Zheng Xiaochuan, et al. A New Non-archie Model for Pore Structure: Numerical Experiments Using Digital Rock Models [J]. Geophysical Journal International, 2013, 195(1): 282-291.
[9] Kennedy W D, Herrick D C, Ydo Tingting. 电性各向异性介质中含水饱和度的计算 [J]. 测井技术, 2001, 25(4): 250-260.
[10] Li X Y, Qin R B, et al. Building a Computational Model of the Cementation Exponent for Complex Porous Reservoirs Based on the Maxwell Equations [J]. Petrophysics, 2013, 54(4): 341-348.
