瞬变电磁测井原理研究V: 径向几何因子

钱科锋, 朱留方, 臧德福, 沈永进, 沈建国, 张付明, 沈洪楚

(1.天津大学电子信息工程学院, 天津 300072; 2.中石化胜利石油工程有限公司测井公司, 山东 东营 257096)

0 引 言

用Doll几何因子可以获得与地层电导率直接相关的二次场响应波形[1-2]。以此为基础,可以对精确解和裸眼井响应中的二次场特征进行分析。精确解所获得的响应包含一次场和二次场。对于瞬变电磁测井,由于其激发频谱幅度比较大的区域频率很低(1 Hz左右),由电磁感应所获得的二次场幅度较一次场小几个数量级。只能用不同地层电导率的响应差波形分析二次场。因为一次场响应与地层电导率无关[3-4],所以在响应差中一次场被去掉,仅仅剩下与地层电导率直接相关的二次场。

对裸眼井,用实轴积分方法可以获得裸眼井的瞬变电磁测井响应,该响应也包含一次场和二次场,同样,用不同地层电导率的响应差也可以获得二次场的响应波形。另外,用不同半径的响应差还可以获得径向上不同半径地层对响应的贡献,该贡献只包含二次场,与Doll几何因子所描述的二次场相似。因此,用这种方法获得径向几何因子,并称其为井条件下的径向几何因子。该几何因子直接从实轴积分法的响应中获得,考虑了井的影响,较Doll几何因子考虑的因素多,是瞬变电磁测井理论的重要结果之一,可以用于径向不同深度地层电阻率阵列测量探头结构以及测量系列的设计,也可用于瞬变电磁测井资料的评价。

1 精确解与Doll几何因子的响应

取地层的电导率为10 S/m,相对磁导率为1,源距为2 m,分别用Doll几何因子和精确解的计算公式计算瞬变电磁测井响应。将上述精确解的响应(实线)和Doll几何因子完全解(包含直接耦合场和二次场)的响应(虚线)绘制在一起得到图1,两者完全重合。图1中(a)、(b)的差异:(a)图计算时选择的频率区间从0开始计算到100 Hz,用到的频率区域比较长,高频成分比较多,响应的峰值接近0.015 V,响应的峰比较尖锐;(b)图计算时选择的频率区间从0开始计算到50 Hz,所用到的频率区域比较短,高频成分少,响应的峰比较粗(具体的频率范围需要根据实验波形确定)。这些现象说明,在以低频为主的瞬变激发响应中,当地层电导率为10 S/m,源距为2 m时,精确解与Doll几何因子完全解均能够对无限大均匀介质的瞬变电磁测井响应进行描述,两者的响应形状完全重合。

图2 精确解与Doll几何因子完全解二次场对比

同样,将电导率分别为10 S/m与1 S/m的不同地层电导率的精确解的响应相减得到的响应差(实线)和Doll几何因子完全解的响应相减所得到的响应差(虚线)绘制在一起进行比较得到图2(a),两者也基本重合,Doll几何因子所得到的响应差幅度稍大。该结果说明,用精确解和Doll几何因子完全响应,通过响应相减的方法获得的二次场也是一样的。该二次场与直接用Doll几何因子计算的二次场[见图2(b)]一致,两者均描述了瞬变电磁响应中与地层电导率有关的响应。可以通过该二次场的测量获得地层的电导率。

精确解和Doll几何因子完全解都是低频近似情况下的解,均不涉及介质的介电常数。在磁导率为常数时,其响应主要受介质的电导率和源距影响。其中介质的电导率越大,对解的影响越明显。同样,源距越大,影响也越明显。图3给出了源距为2 m,电导率分别为10、1 000、3 000 S/m和6 000 S/m时的响应,图3中不同电导率的波形幅度和相位的差别明显。图4是电导率为10 S/m,源距分别为2、20、30 m和40 m时的响应,对其进行了归一化处理,即将响应的几何影响因素(Doll几何因子的响应表达式中有一个因子L3于分母中,该响应乘以了L3)去掉,图4中波形幅度的差异主要是物理衰减造成的,随着源距的增加,波形的到达时间向后移动。

在上述响应中,用Doll几何因子和精确解得到的响应(见图1)完全重合。但是,由于几何因子没有考虑单个圆环之间的相互作用,与精确解会有一定的差别。这些差别在电导率比较大或者源距比较大时表现比较突出。图5是源距不同时2种解的差异。图5(a)是源距为20 m时响应的对比,图5(b)图是其地层电导率分别为1、10 S/m时响应差的对比,差别很明显。图6(a)是源距为2 m,电导率分别为1、1 000 S/m时响应的对比,图6(b)是响应差的对比,差异也很明显。

图3 地层电导率为10(实线)、1 000(长虚线)、3 000(点划线)和6 000(虚线)S/m,源距为2 m时精确解的响应

图4 地层电导率为10 S/m,源距分别为2(实线)、20(长虚线)、30(点划线)和40 m(虚线)时精确解的响应

图5 源距不同时2种解的差异

图6 响应对比和响应差对比图

综上,对于长源距和高电导率地层,几何因子与精确解的差很明显。但是,对于地球物理测井,源距比较短(小于2 m),地层的电导率比较低(小于2 S/m),精确解和Doll几何因子的差别比较小。

精确解和Doll几何因子的差异在电导率比较小时不明显,但是当地层电导率比较大时,差异明显。图7是地层电导率分别为10、100 S/m和1 000 S/m时的响应与地层电导率为1 S/m的响应差除以电导率的差值以后的对比图。从图7上可以看出,电导率为10 S/m时的响应差除以9以后(实线)与Doll几何因子计算的二次场(虚线)很接近,但是,地层电导率为100 S/m时计算的响应与1 S/m计算的响应差除以99以后(点划线)与虚线差异明显;当地层电导率为1 000 S/m时计算的响应与1 S/m的响应差除以999以后(长虚线)的曲线与虚线相差比较大。

图7 地层电导率为1 000(长虚线)、100(点划线)、10(实线)S/m的精确解响应与电导率为1 S/m时的精确解响应的差与Doll几何因子对应的响应差(虚线)的对比(L=2 m)

源距增加时,用Doll几何因子计算的不同源距的响应差(均为虚线)与精确解计算的响应差点划线(L=2 m)、 长虚线(L=4 m)和实线(L=6 m)与对应源距的Doll几何因子计算的响应差虚线相差比较大(见图8)。

对于电阻率测井,由于源距比较短,电导率比较低。因此,Doll几何因子与精确解的差别不明显,在一阶近似的情况下,能够保证处理的精度。

但是,严格解和Doll几何因子均没有涉及到井的影响,没有包含不同电导率和介电常数的圆柱形介质界面的影响。

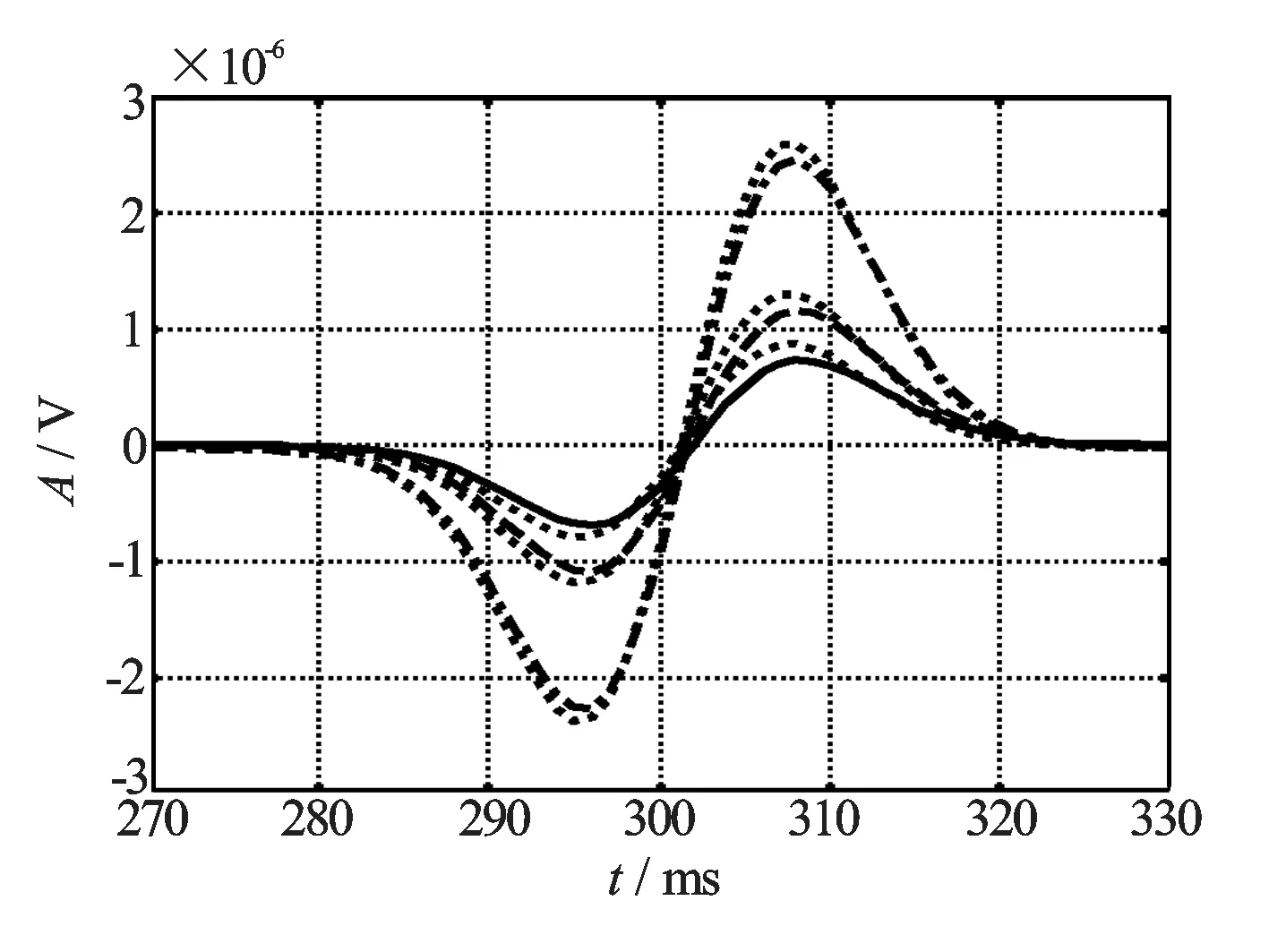
图8 地层电导率为10 S/m的精确解响应与电导率为1 S/m时的精确解响应的差与Doll几何因子对应源距的响应差(均为虚线)的对比,源距L分别为2 m(点划线)、4 m(长虚线)和6 m(实线)

2 实轴积分方法与精确解

为了求裸眼井条件下瞬变电磁测井的二次场,从无限大均匀介质的严格解出发,借助于索末菲积分表达式

(1)

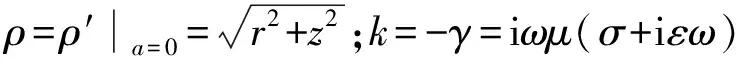
(2)

式中,θ是圆柱坐标圆周方向。从式(2)可以看出,无限大均匀介质的精确解可以表示成z方向的传播函数eikzz和r方向的传播函数K1(lr)的积分。kz是积分变量,在径向多层介质,用相同的积分变量kz,用径向传播函数满足微分方程和边界条件,便可以实现径向多层介质瞬变电磁响应的计算。例如,线圈半径为a、圈数为nk的接收线圈的感应电动势Ua为

Ua=2πankEθ(a,0,L)=-iωμ2πankAθ(a,0,L)

(3)

式中,i是虚数单位。

图9是地层电导率为2 S/m(井内液体与地层取相同的参数值)时的响应,无限大均匀介质的响应式是实线,裸眼井条件下计算的响应是虚线,两者基本上完全重合。(a)图是源距分别为0.1、0.2、0.3 m时响应波形的对比,(b)图是源距分别为0.5、0.6、0.7 m时响应波形的对比。

图9 用球面波和裸眼井积分计算的响应(实线是用球面波计算的,虚线是用积分计算的,地层电导率参数为2 S/m,井半径为0.108 m)

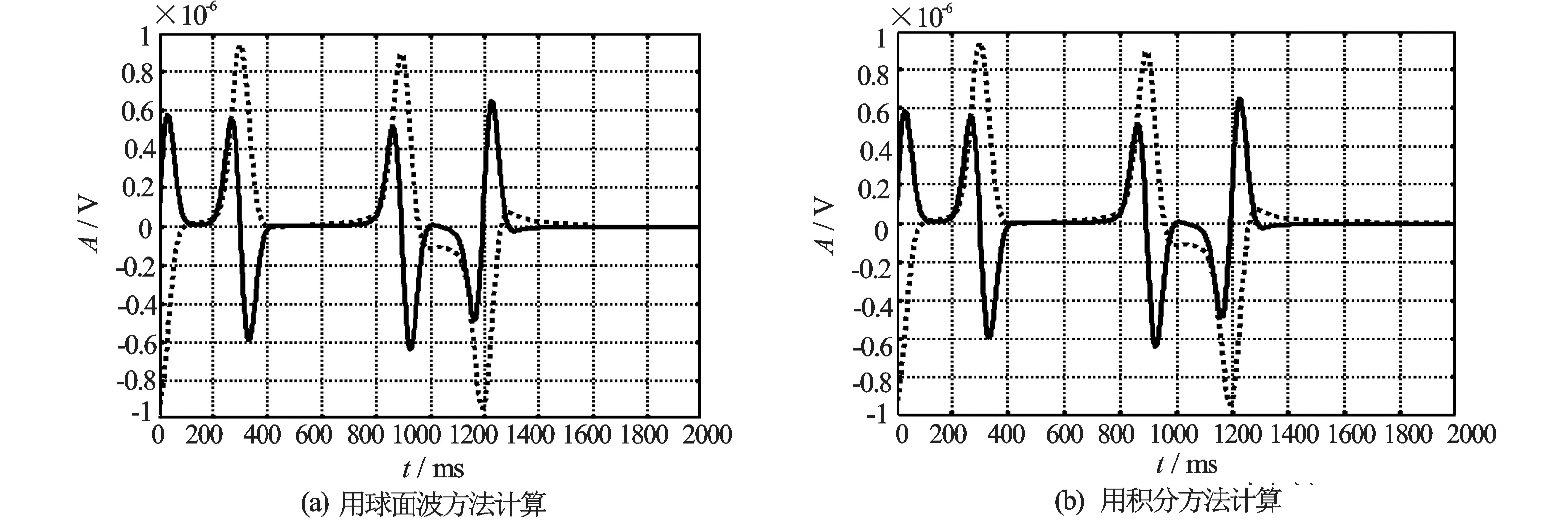
图10 用球面波和积分方法计算的无限大均匀介质的响应(虚线)以及2种不同地层电导率(10、2 S/m)的响应差除以电导率的差(实线),源距0.2 m,虚线除了106

对于二次场,直接用式(3)计算得到的波形如图10所示,其中,虚线是源距为0.2 m处的响应波形,实线是2种不同地层电导率的响应相减以后的结果(二次场),该结果与Doll几何因子所得到的二次场形状相同。

3 裸眼井的响应

裸眼井仅有一个圆柱界面,径向上有2层介质——井内液体和井外固体。需要通过井内的线圈测量井外固体的电导率。建立柱坐标系,设发射和接收线圈均在井内,井内的瞬变电磁测井响应的势函数为

C(kz,ω)I1(lfr)]ei(kzz-ω t)dkzdω

(4)

图11 实轴积分方法计算出的裸眼井中响应波形

取井内液体的电导率为1 S/m、相对介电常数为50;地层的电导率为2 S/m、相对介电常数为5,井内液体和地层的相对磁导率为1。用实轴积分方法计算裸眼井的响应得到图11。其中图11(a)是源距分别为0.1、0.2 m时的响应波形;图11(b)是源距为0.4、0.5 m和0.6 m时的响应波形。从图11可见,随着源距的增加,响应波形的幅度快速减小。不同源距的响应波形形状差别比较小。或者说,不同源距的响应波形形状基本相似:在激发源的突变位置,瞬变电磁测井激发最强,相应地,测井响应幅度也最大;在其他位置,则响应幅度随之减小。

改变地层电导率分别为1、0.5 S/m和0.25 S/m得到图12。其中,虚线是响应波形,实线是地层电导率为1 S/m的响应与地层电导率为2 S/m的响应差;长虚线是地层电导率为0.5 S/m的响应与地层电导率为2 S/m的响应差。点划线是地层电导率为0.25 S/m的响应与地层电导率为2 S/m的响应差。随着地层电导率的减小(电阻率增加),响应差(即二次场)的响应幅度增加。在响应(虚线)变化最快的位置,响应差(二次场响应)的幅度最大。图12(a)图给出了图1所示瞬变激发波形(虚线)的全部响应,图12(b)是第1张图的放大,主要刻画了0到500 ms之间的响应曲线。图13(c)是单个瞬变激发(即只有下降沿)时的响应波形,更加深刻地刻画了瞬变过程的一次场(虚线)和二次场响应波形的形状,其中,二次场与地层电阻率关系密切。响应差中一次场被去掉,仅仅剩下二次场。由Doll的电磁感应理论推导过程知道,发射线圈在地层中感应的环形电动势(一次场)在地层中产生感应电流,该电流在接收线圈中再次产生感应电动势(二次场),因此,二次场响应与一次场响应对时间的导数成正比。

图12 用实轴积分方法计算的裸眼井无限大均匀介质的响应(虚线)以及地层电导率为1的响应减去地层电导率为2 S/m的响应差(实线)和地层电导率为0.5 S/m的响应减去地层电导率为2 S/m的响应差(长虚线)以及地层电导率为0.25 S/m的响应减去地层电导率为2 S/m的响应差(点划线),源距为0.1 m

注意:虚线是除了3 000 000以后与其他线绘制在一起。从图12上可以看出,裸眼井中不同地层电导率的响应相减以后所得到的二次场响应幅度与地层的电导率关系密切,可以用于地层电导率的测量。但是因为瞬变电磁测井的激发波形的频率很低,所以,二次场的幅度仅仅为整个响应的106之一,相对于所能够测量到的波形来讲,其幅度非常小(比感应测井小4个数量级),不能够像感应测井(20 kHz)那样设置信号采集和处理方法,应该根据波形的特点设计全新的仪器结构和信号处理方法,或者通过特殊的刻度方法或装置采集数据,以此为基础,对测量的原始数据进行处理,得到二次场信号。

4 裸眼井的径向几何因子

由式(4)知道,在计算裸眼井的响应时可以改变井的半径,半径越大,井内液体所占据的空间就越大;由几何因子的概念知道,井在瞬变电磁测井响应中所占据的部分就越大。以石油工业上常用的8.5 in*非法定计量单位,1 ft=12 in=0.304 8 m,下同井眼为基础,逐步增加井半径,计算瞬变电磁测井响应,并将增加井径后的裸眼井响应与8.5 in井眼的裸眼井响应相减,去掉直接耦合场(一次场),仅剩下二次场,该二次场主要由8.5 in到所增加的半径的区域的地层所组成。如图13所示,R1是8.5 in井眼的半径(半径大约0.108 m)。首先计算其响应φ1,然后半径开始增加,例如到R2以后,计算井半径为R2时的响应φ2(井内外的物理参数不变)。用φ1—φ2将一次场响应去掉,得到一个二次场,该二次场主要刻画半径R1和R2之间的圆环(空间)对二次场响应的贡献。随着半径的增加,φ1—φ2的幅度逐渐增加,取其响应中的极大值,并比较不同源距时响应差φ1—φ2的极大值随R2的变化规律,可以发现,在源距比较短时,φ1—φ2随半径R2的增加快速增加,很快趋于常数;在源距比较大时,φ1—φ2的极大值随R2的变化规律是,随着R2的增加,其增加缓慢,在R2达到一定深度以后,快速增加,最后又趋于常数。

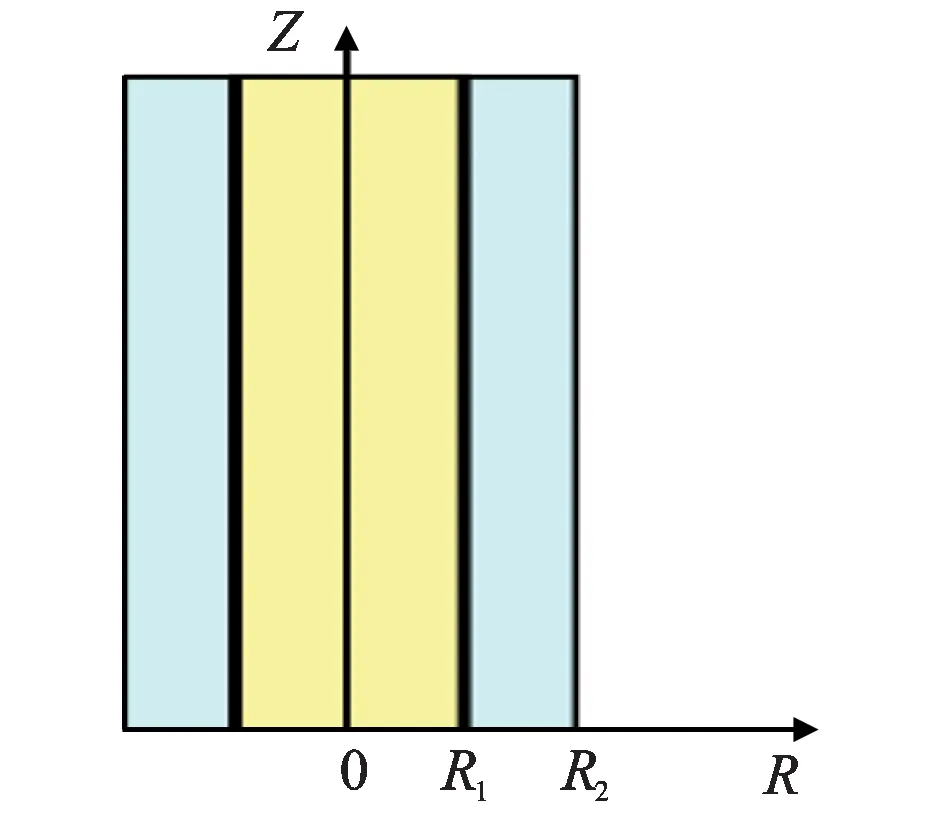
图13 用实轴积分方法获得径向积分几何因子时的物理模型

由感应测井的Doll几何因子所获得的径向积分几何因子知道,随着半径的增加,径向积分几何因子趋于1,不同径向探测深度的线圈系统,其径向积分几何因子趋于1的形状不一样。在径向积分几何因子变化快的半径区间内,径向微分几何因子往往比较大,该区域的圆环(空间圆管)的地层对感应测井响应的贡献大;当径向积分几何因子趋于常数,不随半径改变时,相应地,该半径的径向微分几何因子很小,该区域的圆环(空间圆管)对感应测井响应的贡献很小。

图14 用实轴积分方法获得的径向微分几何因子

基于感应测井Doll几何因子所获得径向积分几何因子,将φ1—φ2的极大值随R2的变化规律归一化后便得到井条件下的径向积分几何因子。用该径向积分几何因子便可以获得相应的径向微分几何因子。图14是用实轴积分方法所获得的瞬变电磁测井的径向微分几何因子,源距从1.004 m到3.804 m(中间等源距增加)。随着源距的增加,径向微分几何因子的极大值向径向深部移动。

5 结 论

(1) 从精确解与Doll几何因子的瞬变电磁测井响应差别认识了Doll几何因子的近似情况:在高电导率地层和长源距响应中误差比较大。从精确解过渡到裸眼井的响应,并用不同地层电导率的响应相减的方法获得了瞬变电磁测井的二次场响应形状,确定了无限大均匀地层的二次场响应特征和裸眼井的二次场响应特征,两者形状完全相同,这说明,①在瞬变电磁测井响应中,井边界的存在对二次场响应影响不大;②在激发波形的突变位置,一次场响应获得极值,在极值的两侧一次场响应变化最快的位置,二次场响应分别具有极大值和极小值2个峰值(一正一负),这是二次场是一次场对时间的导数所致;③2个峰值均与地层的电导率直接相关,是瞬变电磁测井所设计的最佳测量时刻;④二次场响应的峰值与地层的径向半径有关,源距不同,二次场响应与半径的关系不同。

(2) 用这些极值可以获得瞬变电磁测井的径向积分几何因子,该径向积分几何因子描述了瞬变电磁测井的径向探测特征。在源距比较近时,其响应主要由井壁附近的地层电导率所决定,随着源距的增加,其探测深度逐渐加深,当源距为3 m时,其响应主要由1 m半径的地层电导率所决定。

(3) 给出的径向微分几何因子是近似的,它包含了井眼的影响于几何因子中,主要用来分析瞬变电磁测井的径向探测深度,它为设计瞬变电磁阵列接收探头、获得不同径向深度地层电阻率曲线提供了具体的方法。

(4) 瞬变电磁测井的激发频率低(波长比较长),与感应测井相比,其探测深度比较深,获得的近似径向几何因子为研究深探测电阻率曲线的测量系统提供了具体的技术。

参考文献:

[1] 张庚骥. 电法测井 [M]. 北京: 石油工业出版社, 1984.

[2] 戈革, 谢振全. 宏观电磁场论 [M]. 北京: 石油工业出版社, 1980.

[3] Grant I S, Phillips W R. 电磁学 [M]. 刘岐元, 王鸣阳, 译. 北京: 人民教育出版社, 1982.

[4] 别索诺夫 J A. 电工理论基础: 下册 [M]. 陈伟鑫, 沈丽英, 译. 北京: 高等教育出版社, 1986.