基于块稀疏贝叶斯学习的体域网心电压缩采样*
2015-05-09彭向东刘继忠
彭向东,张 华,刘继忠
(1.南昌大学机器人研究所,南昌 330031;2.江西财经大学软件与通信工程学院,南昌 330013)
基于块稀疏贝叶斯学习的体域网心电压缩采样*
彭向东1,2,张 华1*,刘继忠1
(1.南昌大学机器人研究所,南昌 330031;2.江西财经大学软件与通信工程学院,南昌 330013)
为有效提高体域网的实时性和降低体域网的功耗,提出一种基于块稀疏贝叶斯学习的体域网心电压缩采样方法。该方法在体域网框架下,利用压缩采样理论,在体域网的传感节点利用二进制随机观测矩阵对心电信号进行压缩采样,远程监护中心获得采样值之后,利用块稀疏贝叶斯学习重构算法和离散余弦稀疏变换矩阵对心电信号进行重构。实验结果表明,当心电信号压缩率在70%~90%时,基于块稀疏贝叶斯学习的重构算法要比其他重构算法的重构信噪比高出3 dB~21 dB。该方法能有效减少数据采样,减轻后续的数据存储、数据传输压力,提高体域网的实时性。同时该方法具有功耗低,易于硬件实现的优点。
块稀疏贝叶斯学习;体域网;心电信号;压缩采样
人口老龄化的加剧、“空巢”家庭数量的增加以及大量伤残病人的出现给社会带来了诸多问题,其中一个重要问题就是如何为老人及病人提供实时有效的远程健康监护服务。体域网BSN(Body Sensor Network)是解决该问题的较好方案[1-3]。心电ECG(Electrocardiogram)信号,作为人体最为重要的生理参数之一,其在体域网应用中有着非常重要的意义,通过对老人和病人的远程动态实时ECG监测,可以及时发现和预防心血管等突发疾病。然而,利用体域网进行实时ECG监测时,需要采集大量ECG数据,势必会造成体域网实时性的下降和功耗的增加。压缩采样理论较好的解决了该问题[4-6],压缩采样利用欠采样技术,通过减少ECG数据采样,从而减轻后续数据传输的压力,提高体域网的实时性,降低传感节点的数据采集、计算和传输功耗。
针对体域网实时性和传感器节点功耗的问题,Mamaghanian等[7]对基于压缩采样方法和小波方法的ECG体域网功耗进行了对比,结果表明压缩采样方法的功耗更低。其不足在于未有效利用ECG信号的块稀疏特征,导致ECG压缩率的下降,不利于体域网的实时性要求。Khaled等[8]设计了一种基于扩展频谱随机调制预积分器的压缩采样模拟信息转换硬件电路,实现了体域网的低功耗,但其使用基追踪去噪重构算法导致ECG信号重构精度的降低。Dixon等[9]提出一种针对ECG信号的动态阈值方法的1位伯努利压缩采样观测矩阵,通过提高压缩比的方式来降低体域网传感节点的传输功耗,但传感节点的计算功耗较大且不利于硬件实现。DING[10]等提出一种基于压缩采样的体域网心率异常检测方法,该方法在传感节点利用贝叶斯压缩采样对ECG信号进行分类,降低了体域网传输功耗,但由于分类在传感节点进行,势必增加传感节点的负担,从而影响体域网实时性。Zhang等[11]在压缩采样理论框架下利用基于块稀疏贝叶斯学习的重构算法,在获得相同重构精度信号时,能有效降低数据采样率,提高体域网实时性,但其针对的是脑电图信号。刘哲[12]等提出一种基于块稀疏贝叶斯学习的压缩图像融合算法,该算法能有效降低所需的采样数量,获得较优的融合效果,但其针对的是二维图像信号,而非ECG信号。
针对上述问题,为有效利用ECG信号的块稀疏特征,提高体域网的实时性,同时兼顾体域网传感节点的低功耗和易于压缩采样硬件实现,提出一种基于块稀疏贝叶斯学习的体域网心电压缩采样方法。该方法在传感节点端利用随机二进制矩阵对ECG进行观测,观测值被传送至远程监护中心后,再利用离散余弦变换稀疏方式下的变换矩阵和块稀疏贝叶斯学习重构算法对ECG进行重构。通过MIT-BIH心率异常和噪声压力测试数据库中的真实人体ECG数据验证了该方法的有效性。
1 体域网与压缩采样
1.1 体域网
体域网(BSN)是基于无线传感器网络(WSN)的,是人体上的生理参数收集传感器或移植到人体内的生物传感器共同形成的一个无线网络[2]。如图1所示,BSN通过可穿戴或可植入传感器节点采集人体重要的生理信号、人体活动或动作信号以及人体所在环境信息,并利用手机或PDA等智能设备将这些信号和信息传输到身体外部附近的本地基站,最终通过互联网传输到远程监护中心。
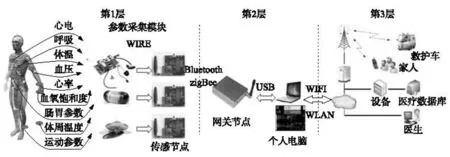
图1 体域网系统架构
为使心血管病人的病情得到及时发现和救助,BSN的实时性研究显得尤为关键。同时由于所有传感节点只能携带有限的电池能源,因此BSN的低功耗设计也是其发展所面临的非常重要的问题之一。本文即利用压缩采样理论,以减少数据采样的方式来提高BSN的实时性和降低传感节点的功耗。
1.2 压缩采样
压缩采样理论指出,设长度为N的信号X在某组正交基或紧框架Ψ上的变换系数是稀疏的,如果用一个与变换基Ψ不相关的观测矩阵Φ:M×N(M≤N)对系数向量进行线性观测得到观测值Y:M×1,那么就可以利用优化求解方法从观测值中精确或高概率地重构始信号X。
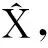
min‖Θ‖0s.t.Y=ACSX=ΦΨTX=ΦΘ
(1)
式中:Θ=ΨTX为变换系数,ACS=ΦΨT为CS信息算子。
压缩采样常用重构算法的类别有贪婪追踪算法、凸松弛法、非凸方法和组合算法等。由于心电信号具有块稀疏特性,为有效提高信号的重构精度,本文采用基于块稀疏贝叶斯学习的重构算法。
2 系统模型及原理
2.1 块稀疏贝叶斯学习模型
基于块稀疏贝叶斯学习BSBL(Block Sparse Bayesian Learning)框架[14]的重构算法的压缩采样模型可描述为:
y=Ax+v
(2)
式中:为A为M×N的感知矩阵,y为M×1维压缩信号,x为N×1维待求的解向量,v为未知的噪声向量。模型(2)中的解向量x具有某些结构,最常见的就是块结构。
(3)
基于式(2)、式(3)的基本压缩采样模型称为块稀疏模型。在这个模型中,解向量x可以划分为g个块结构(每个块结构内的元素个数不一定相同),而x的非零元素则集中于少数几个块内。在BSBL中,假设每一个块xi满足一多元高斯分布:
p(xi;γi,Bi)~N(0,γiBi)
(4)
式中:Bi是一个未知的正定矩阵,用于对该块内的元素之间的相关结构进行建模。γi是一个非负参数,用以控制x的块稀疏,当γi=0时,xi则为0,在学习过程中,大部分的γi将趋近于0,从而促成了解的块稀疏性。同样,假设噪声服从p(v;λ)~N(0,λI)分布,这样就可以利用贝叶斯规则得到x的后验分布,再利用第2类最大似然估计方法可以估计出各个参数,从而最终得到x的最大后验估计值。
2.2 体域网心电压缩采样
基于块稀疏贝叶斯学习的体域网心电压缩采样原理框图如图2所示,为有效提高体域网的实时性和降低体域网的功耗,本文设计的重点为压缩采样中的稀疏方式、观测矩阵和重构算法3个部分内容。其中重构算法采用上述块稀疏贝叶斯学习重构算法,以下描述ECG信号的稀疏方式和观测矩阵设计。
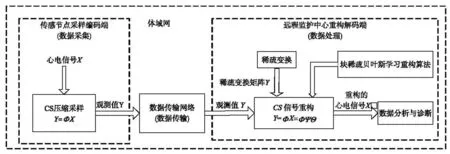
图2 基于块稀疏贝叶斯学习的体域网心电压缩采样原理框图
结合体域网实时性要求高的特点,本文采用离散余弦变换对心电信号进行稀疏。由于离散余弦变换系数取值全部集中在0附近、动态变化范围很小、计算速度快、属于正交变换,因此能较好的满足基于压缩采样的心电信号稀疏表示要求。
考虑到体域网传感节点的低功耗性,本文采用稀疏二进制随机观测矩阵。如式(5)所示,该矩阵每列中1的个数相同且远小于矩阵行数,位置随机,其他值为0。当实际观测时,观测值由该矩阵和心电信号的离散值进行矩阵积运算,由于观测矩阵中只含有1和0元素,0元素不参与运算,1元素的运算相当于心电信号离散值的加法运算,因此两个矩阵的积运算变成了加法运算,而如果利用如高斯随机矩阵等观测矩阵,由于矩阵元素存在非整数项,因此需要处理乘法运算,故选用稀疏二进制随机观测矩阵可以较好的降低传感节点CPU运算的功耗。其次,还可以通过减少观测矩阵中1的个数来降低传感节点的功耗。另外,由于该矩阵的值为1或0,类似电子开关的通或断,也易于硬件电路的实现。
(5)
2.3 实现步骤
基于块稀疏贝叶斯学习的体域网心电压缩采样的实现步骤如下:
步骤1 从MIT-BIH心电数据库中提取ECG数据X来模拟传感节点需要采集的ECG数据。
步骤2 在传感节点端,利用M×N维稀疏二进制随机观测矩阵Φ对N维心电数据X进行压缩采样,根据Y=ΦX得到M维观测值Y。
步骤3 通过数据传输网络将传感节点的M维观测值Y传送至远程监护中心。
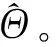
步骤7 调整M的值、块内元素的个数以及稀疏二进制随机观测矩阵每列中1的个数,重复步骤2~步骤6。
3 实验结果与分析
实验中采用的是美国麻省理工学院提供的MIT-BIH心律异常数据库MIT-BIH ADB(the MIT-BIH Arrhythmia Database)[15]和MIT-BIH噪声压力测试数据库MIT-BIH NSTDB(the MIT-BIH Noise Stress Test Database)[16]。这两个数据库均来源于医院的临床病人和门诊病人。MIT-BIH ADB数据库中的每条记录包括MLII和V5两个导联,本实验采用MLII导联数据的前500个采样点,该数据采样频率为360 Hz,信号的增益为200 ADC units/mV,ADC零值为1 024。MIT-BIH NSTDB数据库是包含了基线漂移、肌电干扰和电极运动噪声的ECG信号,每条记录包含了MLII和V1两个导联的数据,本实验采用的是MLII导联数据。由于这些含噪信号前5 min不含噪声,之后每隔2 min交替加载不同信噪比的高频噪声,故本实验取第6 min开始的500个采样点。为显示归一化,实验显示心电图进行了增益和零值处理。
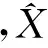
(6)
(7)
本文采用基于BSBL的BSBL边界优化(BSBL-BO)重构算法,以下就BSBL-BO算法性能的影响因素和该算法同其他压缩采样重构算法的性能对比两方面进行实验和分析。
3.1 算法性能影响因素实验和分析
BSBL-BO算法性能的主要影响因素包括:分块时的块内元素个数B、观测矩阵每列中1的个数G和数据压缩率CR,以下就上述3个参数变化时对ECG的SNR影响进行实验。实验中随机选取随机选取MIT-BIH ADB中记录号为122的不含噪ECG信号和MIT-BIH NSTDB中记录号为119e12含噪ECG信号进行测试。
图3为块内元素个数B个数不同时含噪与不含噪信号的重构SNR变化图。测试时,数据压缩率CR固定为70%,观测矩阵每列中1的个数G固定为20,测试块内元素个数B从10到100依次增加10,共10次实验。从图中可以看出,无论是含噪还是不含噪信号,B值的变化对ECG重构SNR的影响不大,故下面的实验中B值取10。
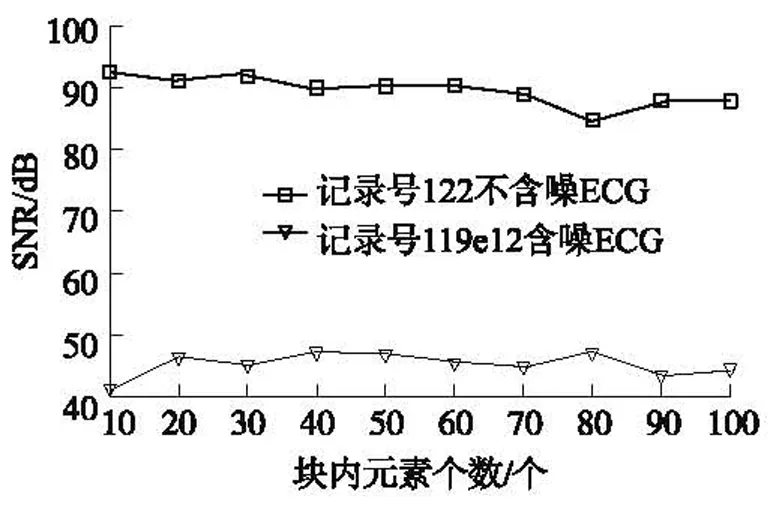
图3 B值不同时的重构SNR对比

图4 G值不同时的重构SNR对比
图4为观测矩阵每列中1的个数G不同时含噪与不含噪信号的重构SNR变化图。测试时,数据压缩率CR固定为70%,块内元素个数B个数固定为10,G从2到29依次增加3,共10次实验。从图4可以看出,无论是含噪还是不含噪信号,G值的变化对ECG重构SNR的影响不大。由于在压缩采样中,传感节点对被测信号的观测主要是完成观测矩阵与被测信号的矩阵积运算,本文采用的是二进制观测矩阵,由于矩阵中的0值不参与运算,故观测矩阵每列中1的个数G越少,传感节点计算量越少,功耗就越低。故G可以选取较小值,以降低传感节点的计算功耗。下面的实验中G值选择10。
图5为数据压缩率CR变化时含噪与不含噪信号的重构SNR变化图。测试时,块内元素个数B个数为10,观测矩阵每列中1的个数G固定为10,CR从10%~90%依次增加10%,共9次实验。从图5可以看出,无论是含噪还是不含噪信号,当数据压缩率CR增大时,ECG重构SNR下降。
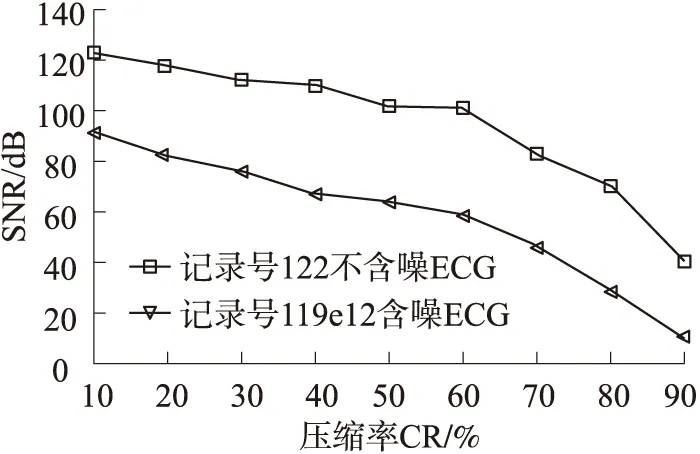
图5 CR值不同时的重构SNR对比
图6 记录号122的ECG重构
3.2 算法对比实验和分析
为有效的验证本文所采用算法的重构SNR高的特点,以下就本文算法与不利用块结构的OMP[17]、Basic Pursuit[18]和利用块结构的Block-OMP[19]3种不同压缩采样重构算法的重构SNR进行对比实验。对比实验分别从固定值的数据压缩率CR和不同值的数据压缩率CR两种情况进行。
在数据压缩率CR为70%的情况下,首先利用记录号122的不含噪ECG信号和记录号119e12的含噪ECG信号进行测试,测试时B的值为10,G的值为10。图6和图7分别为记录号122和记录号119e12在不同重构算法下的ECG重构效果主观视觉图。
从图6中可以看出,本文算法的重构ECG信号要比其他3种算法的重构ECG信号更接近原始ECG信号,并且图7中也显现出类似效果。且总体而言,不含噪ECG信号的重构相对含噪ECG信号的重构而言,除Block-OMP算法之外,其分别对应的失真度均相对小些。因此也验证了本文所采用算法具有更高的重构SNR的优越性。
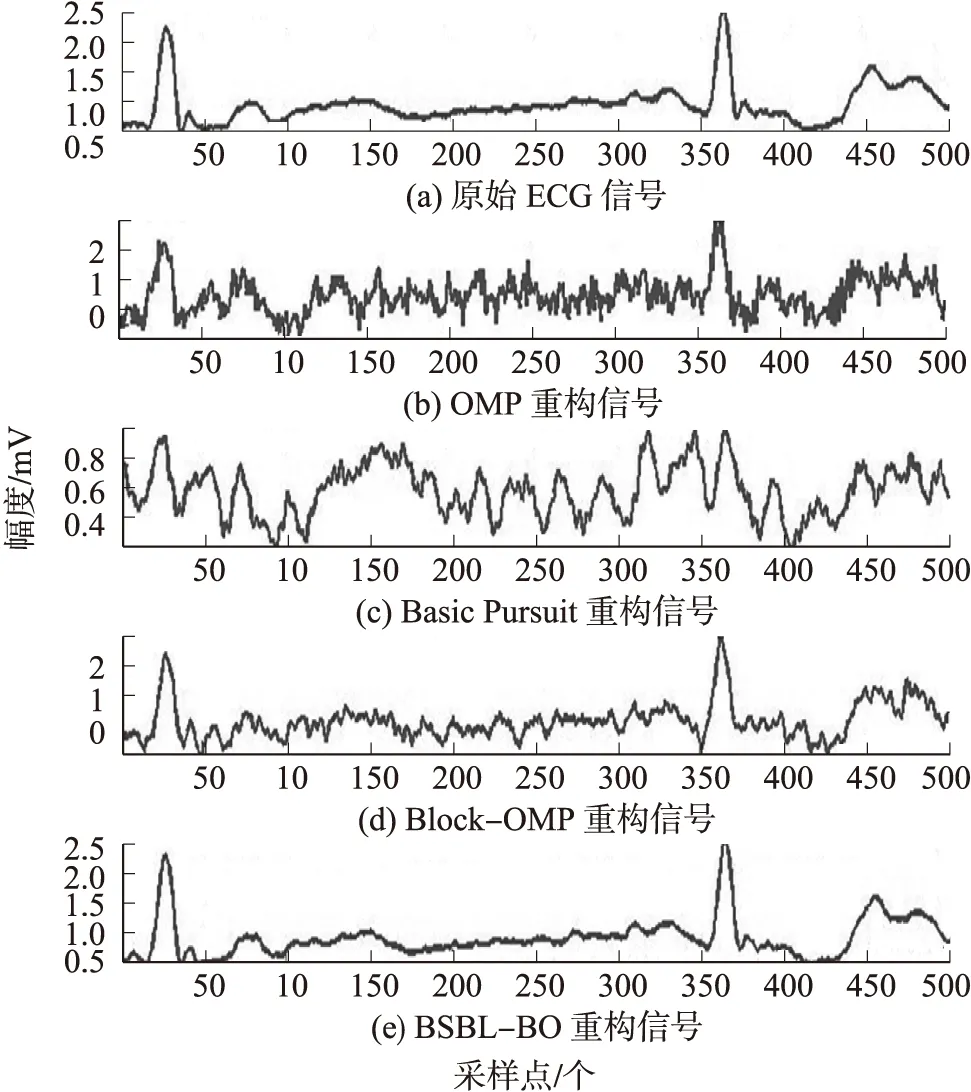
图7 记录号119e12的ECG重构
为进一步验证本文算法的有效性和适用范围,以下从MIT-BIH心率异常数据库48条记录中随机抽取10条,从MIT-BIH噪声压力测试数据库12条记录中随机抽取6条进行ECG重构SNR测试,测试时参数设置和条件与单条ECG数据实验相同,测试结果如表1和表2所示。
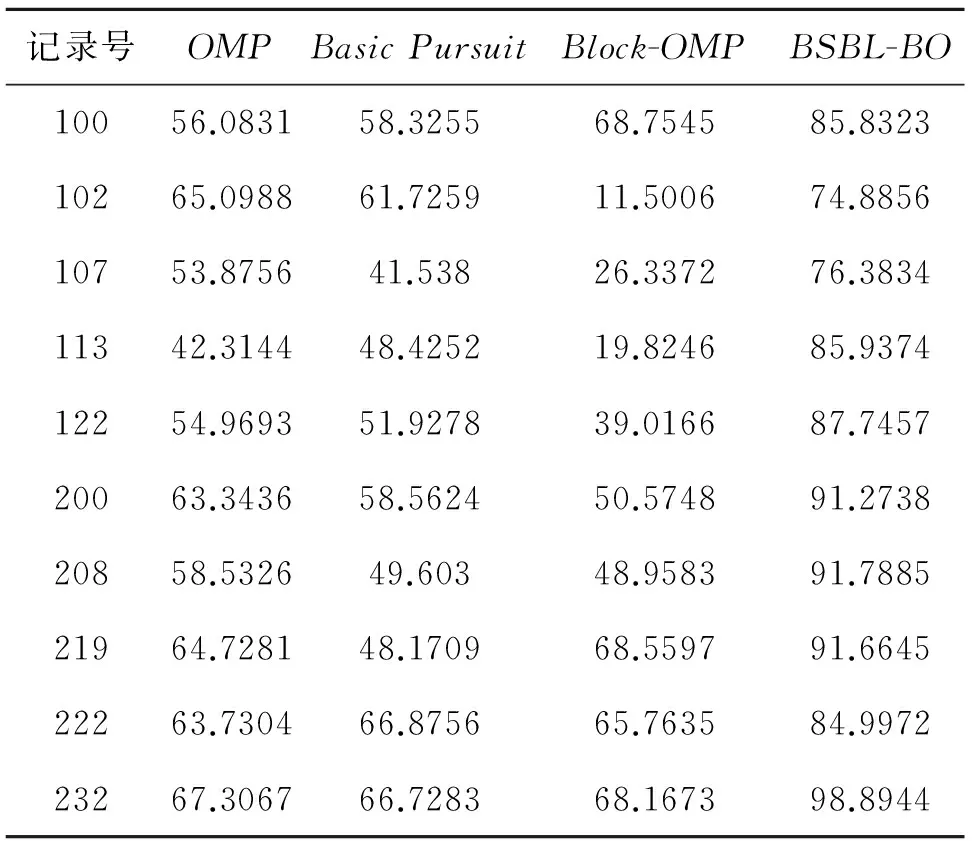
表1 不同重构算法的不含噪ECG数据集重构SNR比较
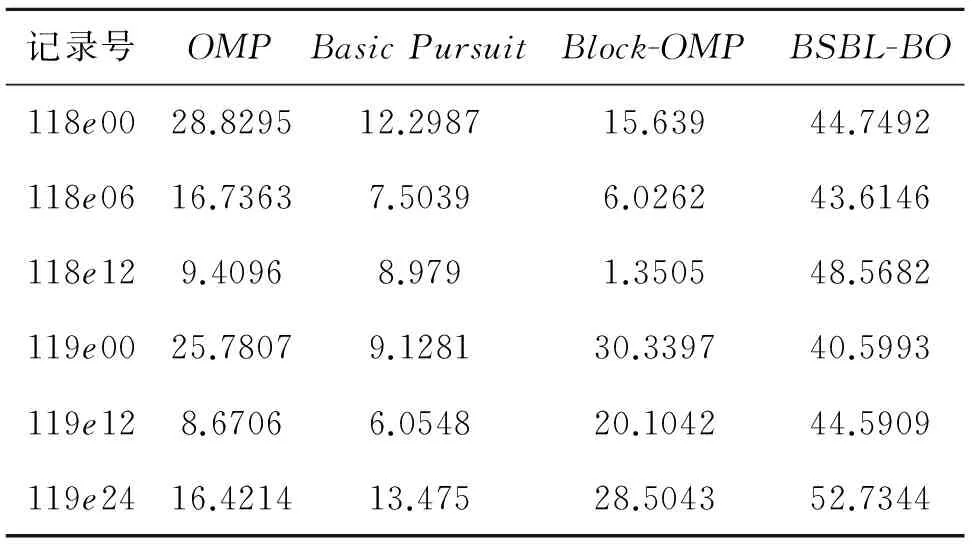
表2 不同重构算法的含噪ECG数据集重构SNR比较
对于不含噪的10条ECG信号,表1数据表明,在不同重构算法下,本文所采用重构算法的重构SNR均比其他3种重构算法高。对于含噪的6条ECG信号,虽然整体重构SNR有一定的下降,但从表2的数据同样可以发现,本文所采用算法对于含噪ECG信号具有同样的适用性。因此,无论是针对单个ECG数据,还是针对ECG数据集,本文所采用的重构算法均具有重构SNR较高的优势。
以上为压缩采样的压缩率为70%的情况下的实验,以下再一步对本文所采用重构算法与其他3种重构算法在不同压缩率下的重构SNR进行对比。实验中所使用的ECG信号为记录号122的不含噪ECG信号和记录号119e12的含噪ECG信号,参数B和G的设置与单条ECG数据实验相同,其实验结果如图8和图9所示。

图8 不同CR和重构算法122的ECG重构
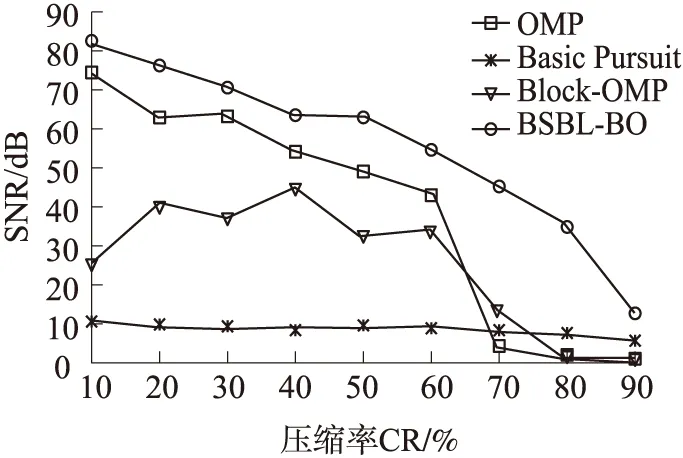
图9 不同CR和重构算法119e12的ECG重构
图8为不含噪ECG信号122在压缩率为10%~90%时,本文所采用算法和其他3种重构算法的重构SNR曲线,图中表明,不同压缩率下,本文所采用算法的重构SNR均大于对应的其他3种重构算法的重构SNR。根据绘图数据计算,当在CR在70%~90%时,本文所采用算法的SNR要比其他3种算法中最好的SNR高出12 dB~21 dB。图9为含噪ECG信号118e12同情况下的重构SNR曲线,图9与图8具有相同的效果。同样根据绘图数据计算,当在CR在70%~90%时,本文所采用算法的SNR要比其他3种算法中最好的SNR高出3 dB~27 dB。
因此,对于含噪与不含噪ECG信号,当CR在70%~90%时,本文采用的过完备字典的稀疏方式要比DCT稀疏基稀疏方式的重构SNR高出3 dB~21 dB。该结果同时也表明,本文所提出的方法与其他压缩采样方法相比,在提供给远程监护中心医生相同SNR的重构ECG信号时,本文方法可以提高压缩率,从而减少数据采样,进而减少数据存储和提高数据传输速度,提高体域网实时性,同时有助于降低体域网传感节点的计算和传输功耗。
4 结束语
本文提出了一种基于块稀疏贝叶斯学习的体域网心电压缩采样方法。在ECG重构时,利用了BSBL重构算法,该算法能有效针对ECG本身的特点,对ECG信号进行分块并考虑块内的相关性,从而能获得更高的重构SNR。在ECG的稀疏时,利用了DCT方式,该稀疏方式的稀疏系数动态变化范围小,计算速度快,有助于提高体域网的实时性。而观测矩阵采用了随机二进制矩阵,该矩阵具有降低计算功耗和易于体域网硬件实现的优点。利用MIT-BIH心率异常和噪声压力测试数据库实验表明,当ECG信号压缩率在70%~90%时,基于块稀疏贝叶斯学习的重构算法要比其他重构算法的重构信噪比高出3 dB~21 dB。同时在远程监护中心得到相同SNR的重构ECG信号时,本文算法能减少传感节点的数据采样,从而减少后续的数据存储数量,传输数量,有助于提高体域网的实时性和降低体域网传感节点的功耗。方法的实现和相关分析为体域网脑电信号和肌电信号的研究提供了支撑。下一步将尝试基于模拟信息转换模型,利用FPGA技术,设计出体域网心电压缩采样硬件平台,进一步验证方法的有效性。
[1]Bao S D,Carmen C Y P,Shen L F,et al. Authenticated Symmetric-Key Establishment for Medical Body Sensor Networks[J]. Journal of Electronics,2007,24(3):421-427.
[2]宫继兵,王睿,崔莉. 体域网BSN的研究进展及面临的挑战[J]. 计算机研究与发展,2010,47(5):737-753.
[3]高翔,郭猷敏,冯天天,等. 基于WBAN的智能康复护理系统设计和实现[J]. 传感技术学报,2012,25(10):1333-1339.
[4]Donoho D L. Compressed Sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[5]Candes E J,Wakin M. An Introduction to Compressive Sampling[J]. IEEE Signal Processing Magazine,2008,25(2):21-30.
[6]石光明,刘丹华,高大化,等. 压缩感知理论及其研究进展[J]. 电子学报,2009,37(5):1070-1081.
[7]Mamaghanian H,Khaled N,Atienza D,et al. Compressed Sensing for Real-Time Energy-Efficient ECG Compression on Wireless Body Sensor Nodes[J]. IEEE Transactions on Biomedical Engineering,2011,58(9):2456-2466.
[8]Mamaghanian H,Khaled N,Atienza D,et al. Design and Exploration of Low-Power Analog to Information Conversion Based on Compressed Sensing[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems,2012,2[3]:493-501.
[9]Dixon A M,Allstot E G,Gangopadhyay D,et al. Compressed Sensing System Considerations for ECG and EMG Wireless Biosensors[J]. IEEE Transactions on Biomedical Circuits and Systems,2012,6(2):156-166.
[10]Ding H,Sun H,Hou K. Direct Cardiac Arrhythmia Detection Via Compressed Measurements[J]. Journal of Computational Information Systems,2012,8(7):2769-2779.
[11]Zhang Z,Jung T P,Makeig S. Compressed Sensing of EEG for Wireless Telemonitoring with Low Energy Consumption and Inexpensive Hardware[J]. IEEE Transactions on Biomedical Engineering,2013,60(1):221-224.
[12]刘哲,顾淑音,南炳炳,等. 一种基于块稀疏贝叶斯学习的压缩图像融合算法[J]. 光子学报,2013,42(11):1365-1369.
[13]Candes E J. The Restricted Isometry Property and Its Implications for Compressed Sensing[J]. Comptes Rendus Mathematique,2008,346(9-10):589-592.
[14]Zhang Z,Rao B D. Extension of SBL Algorithms for the Recovery of Block Sparse Signals with Intra-Block Correlation[J]. IEEE Transactions on Signal Processing,2013,61(8):2009-2015.
[15]Moody G,Mark R. The MIT-BIH Arrhythmia Database[DB/OL]. [2014-07-18]. http://www.physionet.org/physiobank/database/mitdb.
[16]Moody G,Muldrow W,Mark R. The MIT-BIH Noise Stress Test Database[DB/OL]. [2014-07-18]. http://www.physionet.org/physiobank/database/nstdb.
[17]Tropp J A,Gilbert A C. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J]. IEEE Transactions on Information Theory,2007,53(12):4655-4666.
[18]Chen S S,Donoho D L,Saunders M A. Atomic Decomposition by Basis Pursuit[J]. SIAM Journal on Scientific Computing,2001,43[1]:129-159.
[19]Eldar Y C,Kuppinger P,Bolcskei H. Block-Sparse Signals:Uncertainty Relations and Efficient Recovery[J]. IEEE Transactions on Signal Processing,2010,58(6):3042-3054.
ECG Compressed Sampling of Body Sensor Network Based on Block Sparse Bayesian Learning*
PENGXiangdong1,2,ZHANGHua1*,LIUJizhong1
(1.Robot institute,Nanchang University,Nanchang 330031,China;2.School of Software and Communication Engineering,Jiangxi University of Finance and Economics,Nanchang 330013,China)
In order to improve the real-time performance and decrease the power consumption of the body sensor network,this paper proposes an ECG compressed sampling method of body sensor network based on block sparse Bayesian learning. In the body area network framework,the proposed method,using compressive sampling theory,use binary random measurement matrix to compressive sample ECG on the sensor nodes. After measured value are transmitted to remote monitoring center,the block sparse Bayesian learning reconstructed algorithm and the discrete cosine transform matrix and are used to reconstruct the ECG signal. The experiment results show that the SNR which base on block sparse Bayesian learning reconstructed algorithm is 3 dB~21 dB higher than that of the other reconstructed algorithm when the compression rate of ECG is at 70%~90%. The method can effectively reduce the data sampling,the subsequent pressure of data storage and data transmission,and improve the real-time performance of body area network. The method also has the advantages of low power and easy to hardware implementation.
block sparse Bayesian learning;body sensor network;ECG;compressed sampling

彭向东(1975-),男,博士研究生,讲师,主要研究方向为服务机器人,体域网,压缩感知,pxdfj@163.com;

张 华(1964-),男,博士,教授,主要研究方向为机器人技术,智能控制,zhanghua_lab@163.com;

刘继忠(1974-),男,博士,副教授,主要研究方向为智能机电系统与机器人技术,liujizhong@ncu.edu.cn。
项目来源:国家自然科学基金项目(61273282);江西省高等学校科技落地计划项目(KJLD13002)
2014-07-23 修改日期:2014-12-16
C:7230
10.3969/j.issn.1004-1699.2015.03.018
TP393;TP391
A
1004-1699(2015)03-0401-07
