煤矿瓦斯浓度的CAPSO-ENN短期预测模型*

2015-05-09刘雨竹李海霞徐耀松王雨虹

传感技术学报 2015年5期

关键词：瓦斯粒子工作面

付华,刘雨竹,李海霞,徐耀松,王雨虹

(辽宁工程技术大学电气与控制工程学院,辽宁葫芦岛 125105)

煤矿瓦斯浓度的CAPSO-ENN短期预测模型*

付华*,刘雨竹,李海霞,徐耀松,王雨虹

(辽宁工程技术大学电气与控制工程学院,辽宁葫芦岛 125105)

为了准确预测回采工作面的瓦斯浓度,提出云自适应粒子群算法优化Elman神经网络的瓦斯浓度动态预测新方法。利用井下无线传感器网络监测系统采集的回采工作面瓦斯浓度时间序列作为样本,并对其进行数据降噪和相空间重构等预处理。采用CAPSO算法对Elman神经网络的权值、阈值进行寻优运算,建立了回采工作面瓦斯浓度动态预测模型。通过对MATLAB仿真得出结果研究表明:该模型的平均相对变动ARV值为0.000 357,相对均方根误差RRMSE值为0.105 6,对回采工作面的瓦斯浓度预测结果合理且可为矿井瓦斯防治工作提供有效理论依据。

动态预测;瓦斯浓度;混沌特性;无线传感网络;Elman神经网络;CAPSO算法

煤与瓦斯突出是煤矿井下生产的一种强大自然灾害,严重威胁煤矿的安全生产及矿工的生命安全,因此对回采工作面瓦斯浓度的高效精准预测是防治煤矿瓦斯灾害的有力措施之一[1]。目前预测瓦斯浓度的方法主要有混沌时间序列预测[2]、灰色理论预测[3]、支持向量机[4]、人工神经网络[5]、D-S理论[6]等。以上均为基于机器学习模式的预测方法,对于瓦斯浓度短期预测具有一定效用,但由于回采工作面瓦斯浓度具有极大的不确定性,受自然环境条件和开采技术等多种因素影响,且各因素之间的相互作用具有非线性,非平稳性特性,所以传统的线性方法很难达到对瓦斯浓度的精准预测。

在现有的研究成果基础上,采用云自适应粒子群算法对Elman神经网络进行参数优化,解决其预测精度低和收敛速度慢的缺陷,建立可行高效的CAPSO-ENN回采工作面瓦斯浓度动态预测模型。首先对由无线传感器网络监测系统采集到的瓦斯浓度数据采用小波去噪和相空间重构进行预处理,而后采用提出的CAPSO算法对ENN权值及阈值寻优,利用其全局优化能力强、收敛速度快精度高的特性与传统Elman神经网络进行优势互补,经仿真验证分析得到精准高效的回采工作面瓦斯浓度动态预测模型。

1 瓦斯浓度时间序列预处理

由于井下环境的复杂性,无线传感网络监测系统实际监测到的瓦斯浓度时间序列是其浓度体系中各类要素共同作用的结果且其数据信号必然伴有一定的噪声。因此,有必要在进行瓦斯浓度模型预测前,对其滤波去噪和相空间重构。

1.1 瓦斯浓度时间序列TI去噪法滤波

由于传统的非线性小波变换阈值法在数据信号不连续的情况下,会产生伪吉布斯现象,所以采用在此基础上改进的平移不变量小波去噪法[7],对测量处的瓦斯浓度数据进行预处理,去掉其中的干扰信号和噪声信号。其算法表达式为:

(1)

式中:xi为输入的含噪信号,i=0,1,…n-1;Sh为对信号xi做h距离的时域平移,即(Shxi)=x(i+h)time为所得平移信号;T表示对信号应用阈值法进行去噪,则去噪信号为T(Shxi);S-h(T(Shxi))为经反向循环平移后的去噪信号;Ave表示“平均”;Hn={h|0≤h≤n},h为正整数。

经TI去噪法处理后的小波信号平滑性更好,且避免了信号跳变点的伪吉布斯现象。

1.2 瓦斯浓度时间序列相空间重构

由于一维瓦斯浓度混沌时间序列中包含大量信息,因此必须对其维数进行扩充及延拓,使其扩展到更高维的空间中,才可还原其中蕴含的所有变量的运动轨迹[8]。由Takens定理可知,相空间重构技术的关键就在于选取最优的延迟时间τ和嵌入维数m。

由于两参数的相关性及将其分开考虑的算法的矛盾性,提出利用相空间微熵率法同步求取重构参数,即以最小化微熵率的方法同时确定τ、m两个参数。

给定样本数据序列x(t)(t=1,2,…,n)、Ns个替代数据xs,i(t)(i=1,2,…,Ns)。微熵定义为:

(2)

式中:ρj为第j个延迟向量与其最近邻点间的欧氏距离;CE≈0.5772为欧拉常数。则可得给定序列微熵率为:

(3)

式中:N(N=n-(m-1)τ)为延迟向量个数;<·>i为求解Ns个替代数据微熵H(xs,i)的平均值算子。τ和m在一定范围内变化,则可根据式(3)求出在两参数给定变化范围内的微熵率,在所得结果中选出最小微熵,此时其所对应的τ、m值即为所求最优参数。则其重构的相空间向量为:

Xi=(xi,xi+τ,…,xi+(m-1)τ)∈Rm

(4)

式中:i=1,2,…,M,M=N-(m-1)τ。

2 CAPSO-ENN耦合算法原理

Elman神经网络由于其自身特殊的动态反馈环节和递归作用,不仅能够解决静态网络的建模问题,还可以实现非线性动态系统的映射并在更直接的角度反映系统的动态性能。相较于前馈神经网络,具有更强的数据处理能力和网络稳定性,更适合瓦斯浓度动态预测系统的辨识与建模[9]。然而,正是由于其自身网络结构复杂,使Elman神经网络仍存在学习速度较慢、易于“早熟”收敛、鲁棒性较差等缺陷。据此提出具有强大全局寻优能力的CAPSO算法与ENN进行有机结合,形成CAPSO-ENN耦合算法,提高ENN的学习效率及收敛速度,进而改善ENN的辨识性能与预测精度。

2.1 Elman动态反馈神经网络

Elman神经网络[10]是一种动态递归反馈式网络,由输入层、隐含层、输出单元和特殊存在的联系单元组成,此联系单元用来记忆隐含层单元之前时刻的输出值,实现了该神经网络的动态记忆功能,使其更适合处理时间序列。其网络结构如图1所示,

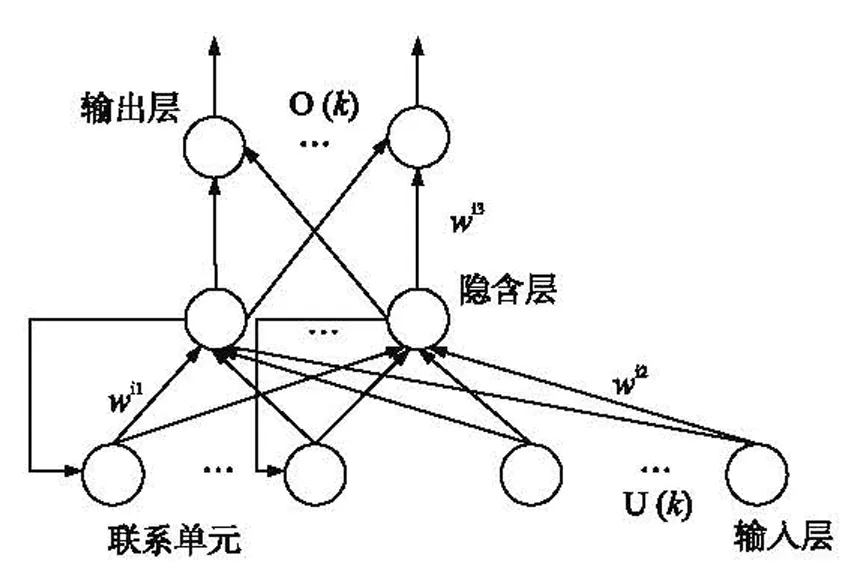
图1 Elman神经网络结构图

数学模型可表示为:

H(k)=f(wi1C(k)+wi2u(k-1))

(5)

C(k)=αC(k-1)+H(k-1)

(6)

O(k)=g(wi3H(k))

(7)

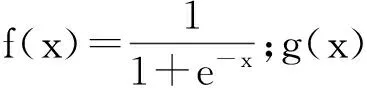
采用误差反向传播算法进行权值修正,若利用n个样本进行训练学习,则将误差平方和函数作为学习指标:

(8)

式中:

(9)

2.2 云自适应粒子群算法

2.2.1 正态云模型的数学表达

云模型[11]是定性概念与其定量表示之间的一种相互转换手段,主要体现了知识表达的不确定性概念和确定数据之间的模糊性以及随机性。正态云模型是一个正态分布且具有稳定倾向性的随机数集合,记为N3(Ex,En2,Hn2),其中Ex、En、Hn为云的3个特征参数,分别为期望值、熵和超熵。

生成云滴的软件或硬件成为云发生器。采用X-条件云发生器,其生成算法为:

①输入云特征参数Ex、En、Hn和指定值x0。

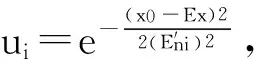
④重复步骤②～④直到得到n个云滴。

2.2.2CAPSO算法的权值调整策略

设粒子群总数目为pzong,总迭代次数为KM,在第k次迭代中粒子xi的位置适应值为f(xi)。根据式(4)将粒子种群分为2部分,即距离最优粒子较近和较远的部分。

(10)

①对于距离最优离子较远部分,即当f(xi)>fav时,算法往往处于迭代前期,为避免算法停滞在全局最优解,运用梯度思想进行惯性权值更新,其表达式为:

(11)

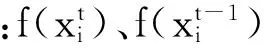
(12)

②对于距离最优粒子较近部分,即当f(xi)≤fav时,算法往往处于迭代后期,采用X-条件云发生器参与自适应调整ω值,令Ex=fav,En=(fav-fmin)/C1,Hn=En/C2,其中C1、C2为加速因子。并利用梯度思想与其结合选取合适的惯性权重,则其更新策略为如式(13)所示:

(13)

由以上①、②两点可知,迭代初期,惯性权重ω取最大值,保证强大的全局搜索能力,随着迭代次数增加,粒子群最优解不断更新并迅速达到fav以下,此时ω值将会随之按正态云模型方式逐渐减小,具有随机性和稳定倾向性,并引入的梯度思想来避免算法陷入局部最优解。

2.3 CAPSO优化Elman神经网络

由于标准粒子群算法实现方便,参数少、结构相对简单,收敛速度快,被广泛应用于模型参数的优化选择[12]。但应用其对瓦斯浓度进行预测时,常表现为复杂的混合优化问题,PSO算法无法满足实际情况的需要。为提高算法的全局搜索能力和收敛精度以及收敛效率引入云模型算法和梯度思想与标准PSO算法相结合,从迭代早期到后期完成对粒子群算法的全方位改进,得到云自适应粒子群算法,提出新的惯性权重调整策略,避免粒子过早的陷入全局最优解,其优化Elman神经网络步骤如下:

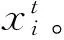
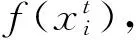
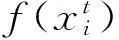
Step 5:判断是否满足终止条件:若满足最大迭代次数或指定精度,则执行Step 6,否则循环执行Step 2。

Step 6:输出xgbest及其目标值,算法结束。

3 建立瓦斯浓度动态预测模型

回采工作面的瓦斯浓度预测是一个动态非线性预测问题,由此建立的预测模型实质就是利用已测得的瓦斯浓度数据通过具有动态反馈功能的CAPSO-ENN耦合算法在线学习训练,从而拟合出瓦斯浓度预测系统来预测未来一段时间回采工作面的瓦斯浓度。为准确反应非线性时变系统的输出、输入间关系,需在建立模型时将表征该时变系统的动态特性引入其中。最有效的方式就是将系统的历史输入和输出量作为一部分输入值再次引入辨识模型。为满足预测的实时性,选用最新的n个数据作为样本,并对从前建立的适应度函数优化从而达到动态预测的目的。

3.1 基于CAPSO-ENN耦合算法的建模

由于Elman神经网络存在收敛速度慢且易陷入局部最优解的问题,提出利用云自适应粒子群算法对其网络权值及阈值进行寻优,其优化算法实现步骤为:

①初始化群体。根据辨识对象对粒子群的各个参数进行随机初始化设置,并设置ENN初始权值、阈值。

②粒子更新调整。根据2.2.2节所述对粒子位置进行更新调整。

③输入训练样本Y(x)到CAPSO-ENN耦合算法中,计算得出Elman神经网络实际输出函数yk(x)与训练样本的期望输出函数间的训练误差e(x),训练目标为使误差达到最小,则适应度函数确立为:

(14)

依式(8)计算相应适应度,根据此值运用云自适应算法对动态神经网络进行在线训练。

④经过多次迭代运算后,训练完成,得出粒子群最优解,即作为最优Elman神经网络的权值和阈值{ω,θ}。

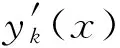
3.2 预测模型结构

根据通过无线传感网络瓦斯浓度监测系统[13]采集到的数据样本,首先对其进行TI小波去噪,再重构该数据序列相空间,而后建立基于CAPSO-ENN的非线性映射关系,对未来一段时间内的回采工作面瓦斯浓度做出精准预测。将CAPSO优化算法寻优搜索所得的适应度最好的一组网络权值作为预测网络模型的权值、阈值向量反馈到Elman神经网络得到瓦斯浓度预测模型,其结构如图2所示。

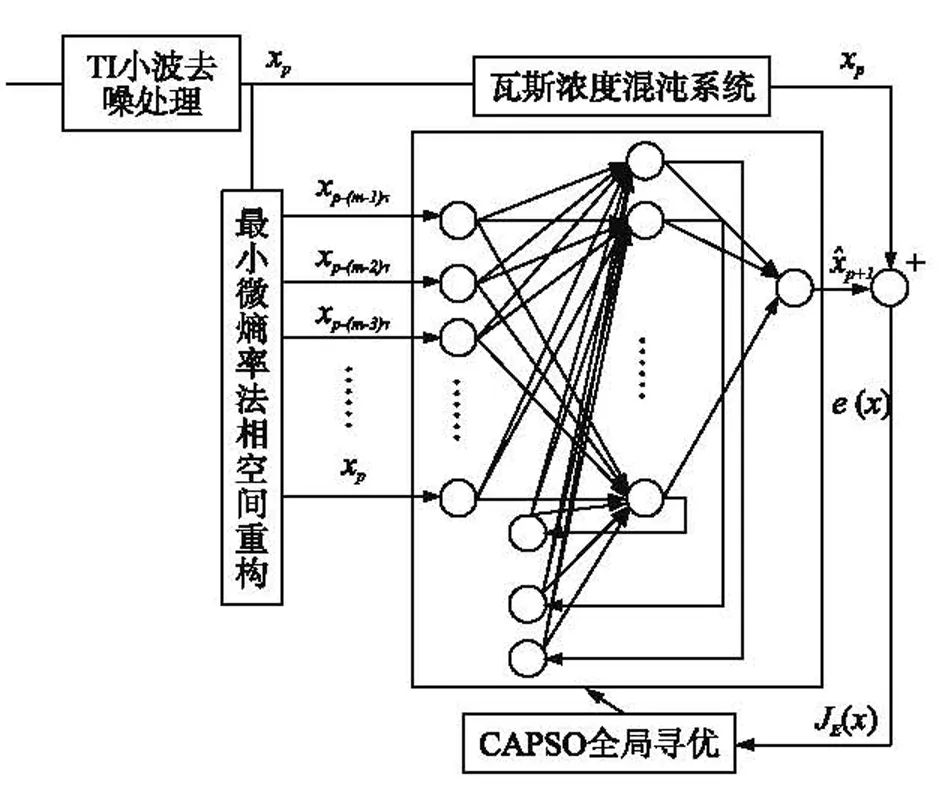
图2 瓦斯浓度预测模型的结构

4 瓦斯浓度预测仿真试验

文中所采用的瓦斯浓度数据来自山西焦煤官地矿的16 403综采工作面KJ90N煤矿安全监测系统。采用了PXWAE数字化瓦斯浓度监测仪,包括传感器(频率150 kHz),前置放大器(增益为40 dB),主放大器(增益为0)以及采集卡,采集到2014年8月份某天某时段的300采集点。

瓦斯浓度原始曲线如图3所示。采用1.1节所述TI去噪法对原始瓦斯浓度时间序列进行去噪处理,最大程度还原瓦斯浓度测量点处的瓦斯浓度,其仿真曲线如图4所示。

图3 瓦斯浓度原始数据曲线

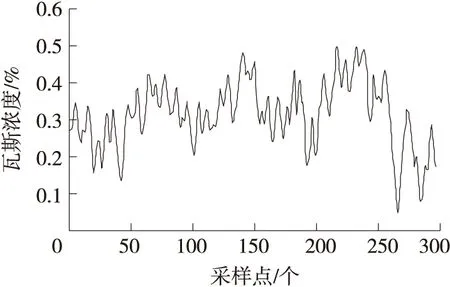
图4 去噪后瓦斯浓度序列数据

利用Wolf方法求取瓦斯浓度时间序列的最大Lyapunov指数以实现对其混沌特性的判别[14],求得本时间序列的λ=0.034 736>0,则此瓦斯浓度时间序列具有混沌特性。

4.1 预测模型初始化及数据处理

试验数据样本初始化,即将前280个瓦斯浓度值作为学习训练样本,后20个瓦斯浓度值作为测试验证样本。利用2.2节所述最小微熵率法对训练样本数据序列求取微熵率并最小微熵对应的m=6,τ=4。通过相空间重构过程后可得260组学习训练样本建立模型。

初始化Elman神经网络参数为:输入层节点数S1=6;隐含层和联系单元节点数S2=7;输出层节点数S3=1。其传递激励选用sigmoid函数,自变量定义域[0,1],由于sigmoid函数在[0,0.1]、[0.9,1]两个值域内的变化曲线较平坦,选取归一化区间为[0.1,0.9],其归一化公式为:

(15)

网络训练预测完成后,对所得结果数据实行反归一化处理,即

(16)

式中:X为原始数据;Xmin、Xmax为其最小值和最大值;T为经变换得出的数据。

粒子群规模为pzong=50;最大迭代次数KM=500;加速因子C1=C2=2。

4.2 预测过程

规定模型训练过程的允许误差范围在10-4以下。

CAPSO-ENN模型的训练收敛效果如图5所示,通过图中曲线可以看出,CAPSO优化Elman神经网络时,由于采用了云理论与梯度思想相结合的权重调整策略,使模型约迭代到350次时就已达到了训练误差的精度要求范围,且能够更迅速的跳出局部最优解,为验证CAPSO算法优越的收敛性能,将其与传统PSO算法进行对比,相较于粒子群优化算法PSO(Particle Swarm Optimization),其寻优速度更快且收敛精度更高,明显的提高了Elman神经网络的学习效率。

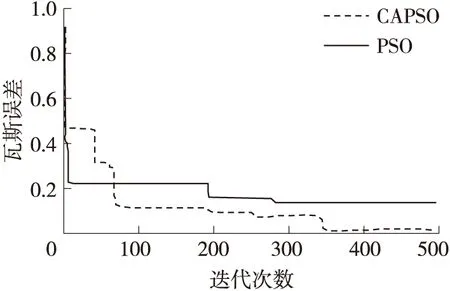
图5 CAPSO与PSO的收敛性对比

4.3 仿真结果分析

通过MATLAB2012a对预测模型进行算法仿真试验,分别采用PSO-ENN和CAPSO-ENN模型对样本数据序列后20个待测点的预测结果对比如图6所示。

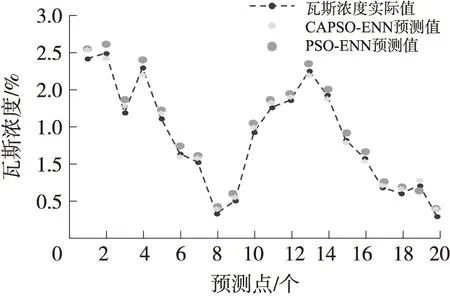
图6 样本数据序列瓦斯浓度预测值与实际值对比

为验证所建模型的有效性和优越性,选取传统常用的PSO-ENN模型进行预测效果对比,由图6可以看出在预测的初期阶段PSO-ENN模型的预测效果较好,然而到了预测后期,预测值偏离实际值较为突出。而运用CAPSO-ENN模型得到的浓度预测值和瓦斯浓度的实际值间整体拟合性更优,与PSO-ENN模型相比更接近瓦斯浓度的实际真实值。

以相对均方根误差RRMSE(Relative Root Mean Square Error)和平均相对变动值ARV(Average Relative Variance)作为指标来衡量预测模型的预测精度和泛化能力,其计算公式为:

(17)

(18)

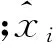
为保证所建模型的预测性能的可行性、有效性和高度的预测效率,分别选用单一Elman神经网络和PSO-ENN模型采用瓦斯浓度样本数据建模运算,得出预测结果后与CAPSO-ENN模型进行对比,结果如表1所示。

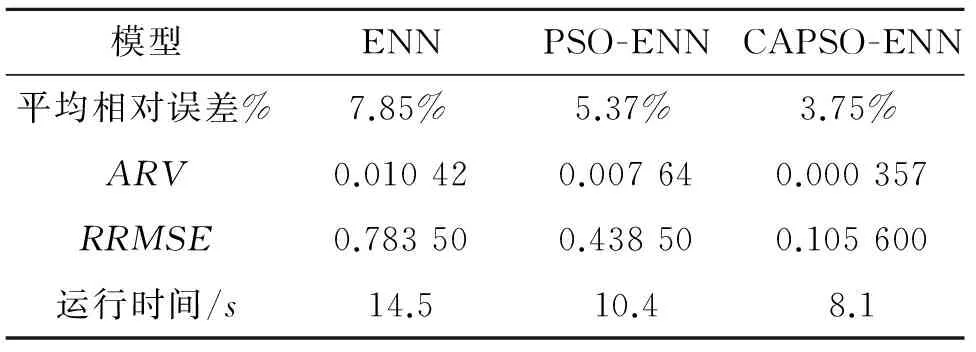
表1 3种预测模型预测效果对比分析

从表1可以看出,CAPSO-ENN模型的预测平均相对误差明显较其他两种方法低,并且具有更强的泛化能力,且运算时间较ENN模型少了6.4s,较PSO-ENN模型少了2.3 s,求得其ARV值为0.000 357,RRMSE值为0.105 6。说明所建模型在满足实际矿井安全生产的精度要求的同时,可实现回采工作面瓦斯浓度的精准高效预测。在1min的采样间隔前提下[15],小于10s的建模耗时能够保证模型的有效更新,即预测的自适应性得到了保证,为实际瓦斯浓度实时监测预警系统的构建提供强大的理论依据。

5 结论

本文利用Elman神经网络具有动态反馈环节的优越性,将基于云模型理论的粒子群算法与Elman神经网络有机结合,改善了其易陷入局部最优解和学习速度慢的缺陷,有效提高了Elman神经网络的预测效率与预测精度。利用建立的CAPSO-ENN耦合算法建立的动态预测模型对井下回采工作面瓦斯浓度进行仿真试验,结果表明,该模型具有较强的泛化能力且预测精度与效率明显高于其他方法。能够准确可靠的对井下瓦斯浓度演化趋势进行提前预测,为实际技术应用提供了强有力的理论依据。

[1] 吕品,马云歌,周心权. 上隅角瓦斯浓度动态预测模型的研究与应用[J]. 煤炭学报,2006,31(4):461-465.

[2]程健,白静宜,钱建生,等. 基于混沌时间序列的煤矿瓦斯浓度短期预测[J]. 中国矿业大学学报,2008,37(2):231-235.

[3]基于灰色自记忆原理的煤矿瓦斯浓度预测[J]. 科技导报,2010,28(17):58-62.

[4]张剑英,许徽,陈娟,等. 基于粒子群优化的支持向量机在瓦斯浓度预测中的应用研究[J]. 工矿自动化,2010,(10):32-35.

[5]王其军,程久龙. 基于免疫神经网络模型的瓦斯浓度智能预测[J]. 煤炭学报,2008,33(6):665-669.

[6]邵良杉,付贵祥. 基于数据融合理论的煤矿瓦斯动态预测技术[J]. 煤炭学报,2008,33(5):551-555.

[7]康金钟,康志伟. 基于平移不变的小波变换去噪快速算法[J]. 微电子学与计算机,2005,22(9):24-26.

[8]Song J,Meng D,Wang Y. Analysis of Chaotic Behavior Based on Phase Space Reconstruction Methods[C]//Computational Intelligence and Design(ISCID),2013 Sixth International Symposium on. IEEE,2013,2:414-417.

[9]付华,姜伟,单欣欣. 基于耦合算法的煤矿瓦斯涌出量预测模型研究[J]. 煤炭学报,2012,37(4):654-658.

[10]Lin F J,Teng L T,Chu H. Modified Elman Neural Network Controller with Improved Particle Swarm Optimization for Linear Synchronous Motor Drive[J]. 2008,2(3):307-310.

[11]刘洪霞,周永权. 一种基于均值的云自适应粒子群算法[J]. 计算机工程与科学,2011,33(5):97-101.

[12]Abdel-Kader R F. Genetically Improved PSO Algorithm for Efficient Data Clustering[J]. Machine Learning and Computing(ICMLC),2010,10(11):71-75.

[13]李纪榕,李福进,吴艳微,等. 基于无线传感网络的煤矿安全监测系统设计[J]. 传感技术学报,2011,24(9):1336-1340.

[14]张文超,谭思超,高璞珍. 基于Lyapunov指数的摇摆条件下自然循环流动不稳定性混沌预测[J]. 物理学报,2013,62(6):61-68.

[15]付华,李文娟,孟祥云,等. IGA-DFNN在瓦斯浓度预测中的应用[J]. 传感技术学报,2014,27(2):262-266.

Short Term Forecasting Model of Gas Concentration in Coal Mine Using the CAPSO-ENN*

FUHua*,LIUYuzhu,LIHaixia,XUYaosong,WANGYuhong

(Faculty of Electrical and Control Engineering,Liaoning Technical University,Huludao Liaoning 125105,China)

In order to accurately predict the gas concentration in mining working face,a new dynamic prediction method of gas concentration which based on the cloud adaptive particle swarm algorithm on optimizing Elman neural network was proposed. The samples came from gas concentration time series which were collected by the underground wireless sensor network system in working face. The pretreatment of data noise reduction,phase space reconstruction and so on was carried. The weights and threshold of Elman neural network was optimized by CAPSO algorithm,and the dynamic prediction model of gas concentration in mining working face was established. Through the research on the MATLAB simulation results show that:The model of the relative change of average ARV value is 0.000 357,the relative root mean square error of the RRMSE value is 0.1056,the heading stope gas concentration prediction provides an effective theoretical basis for reasonable results and for mine gas prevention and control work.

dynamic prediction;gas concentration;chaotic characteristic;wireless sensor networks;Elman neural network;CAPSO algorithm