较深覆盖层基坑悬挂式截渗墙控降水优化研究

2015-05-09张丽伟

西北水电 2015年6期

张丽伟，滕凯

(1.齐齐哈尔市河道管理处,黑龙江省齐齐哈尔市 161006;2.齐齐哈尔市水务局,黑龙江省齐齐哈尔市 161006)

1 问题的提出

由于水工建筑物作用的特殊性，大都建于江河沿岸的一级阶地或河道的主槽之上，其基土条件或是典型的二元结构(即上部由透水性弱、强度相对较低的黏性或沙性土组成；下部则由透水性好、强度相对较高的砂砾即卵石层组成)或是单一的强透水层。因此在这类地区修建水利工程，为防止由于地下水渗入基坑产生流沙、管涌、突涌及边坡失稳等现象发生，保证施工安全和施工质量，工程上必须采取有效措施对基坑内地下水位进行控制和降排。目前，工程上主要采取的控降水措施有两大类：一类是单纯的强降水，即将基坑区域内的地下水位通过井点或明排抽降至基底开挖面以下；第二类是通过在基坑周边实施墙体截渗(全封闭、半封闭及悬挂式)与降水相结合的措施将地下水位降至基底开挖面以下。

与建筑及市政工程的深基坑相比，水利工程基坑具有更强的透水性，主要是：① 开挖作业面积大，一个独立基坑面积可以在几百平米至几万平米，甚至达到几十万平米；② 透水性强，一般情况下基坑透水层的渗透系数多在50～350 m/d，甚至达到800 m/d(如黑龙江北部引嫩渠首工程[1])；③ 周边环境约束相对较小，由于水工建筑物多建在远离城镇(或其它建筑物)的偏僻之处，因此对基坑周边的沉降限制相对较小。基于上述原因，水利工程基坑的控降水难度及投资明显大于其它工程。因此，在保证基坑及周边工程安全的前提下，如何降低基坑工程的控降水费用一直受到相关学者的关注。文献[2-7]分别以基坑总涌水量最小或基坑控降水费用最低为目标函数，给出了第一类基坑控降水相应的优化设计方法，具有较好的实用意义。而对于设有悬挂式截渗墙类型基坑控降水优化设计的研究则相对较少，文献[8-9]以基坑外某一点的沉降控制及工程安全为约束条件，提出了止水帷幕结构设计的优化方法，但对降低整个基坑的控降水费用而言尚不够全面。文献[10]根据截渗墙深与施工工期及基坑内最大出逸水力坡降的关系，通过图解法提出来确定最小截渗墙深的计算方法，但由于用此方法确定的墙深并非最经济墙深，对目标函数的选择及表达式的确定尚需进一步研究。文献[11]提出了以基坑控降水费用为目标函数，以基坑周边环境要求为约束条件的优化设计思路，但由于文内并未给出可以借鉴和引用的具体计算公式及求解方法，实际应用意义不大。另一方面，目前用于设有截渗墙基坑渗流分析的方法均为有限元法或数值模拟法[12-14]，对计算边界条件及参数选定要求较高，计算运行环境相对比较复杂，对应用者的基本技能要求较高，不便实际应用。因此，提出一种便于推广应用且更适合水利工程基坑控降水设计的优化方法十分必要。本文在对较深厚覆盖层设有悬挂式截渗墙基坑渗流条件对比分析的基础上，利用经典的井流公式及达西定律建立了基坑内外水量平衡方程，提出了以施工现场提排水设备的现有能力、周边环境、墙体施工工期、防管涌破坏、防坑底突涌破坏、防潜蚀破坏及防流砂破坏为约束条件的基坑控降水费用目标函数模型，并采用非线性规划理论，提出了获得与基坑控降水总费用最低相对应的截渗墙最优贯入深度及其他相关参数的求解方法，计算过程简单直接，便于实际工程推广应用。

2 数学模型的建立

2.1 基坑控降水费用数学模型

设有悬挂式截渗墙水利工程基坑的渗入水量主要为2部分：一是通过截渗墙墙端以下透水层渗入基坑的水量；二是通过截渗墙墙体渗入基坑的水量。因此，该类工程基坑控降水费用主要由截渗墙的成墙、降水井(机泵设备)及排水动力运行(包括管理费)等费用。增加截渗墙体的垂直贯入深度可有效减小地下水向基坑的渗入量，从而减小基坑的降水运行费及相应的设备或成井投资，但随着截渗墙体贯入深度的增加，基坑用于截渗措施的工程投资也将明显增大，因此，如何选择截渗墙的贯入深度使基坑的总控降水费用最小，则是基坑控降水设计的关键所在，为此，本文提出建立以下基坑控降水目标函数(考虑降水设施及机泵折旧费对优化成果的分析影响不大，与运行管理费合并统一按降水设施及运行费的10%计取)：

(1)

式中：F(S)为基坑的控降水总费用，元；Bl为截渗墙第l段的水平长度，m；ll为第l段截渗墙墙体的总入土深度或高度，m；p为截渗墙的单位平米造价，元/m2；T为基坑控降水的总历时，d；β为水泵的降水台时费用，元/(台·d)；q为单台水泵的日排水总量，m3/d；Q为基坑整个控降水期的平均日排水量，m3/d；f为每眼降水井的成井及机泵设备投资，元/每眼井。

2.2 基坑涌水量计算

由图1可见，较深厚覆盖层设有悬挂式截渗墙基坑的涌水量主要来自2个部分，分别为由截渗墙底端至不透水层绕渗和由截渗墙墙体本身渗进入基坑的渗流量。由于通过截渗墙墙体渗进入基坑的渗流量很小，可不计算其影响。

图1 实际基坑降水示意图

由于截渗墙在平面上为沿基坑边线布置的类似于封闭式的管形结构，因此，可将其视为一个降水井的井壁，基坑排水后地下水绕过墙底至下部隔水层之间的透水层进入基坑内，使基坑周边水的流态及流势如同一个潜水非完整井，并可将墙底与隔水层之间高度的0.7倍视为过滤器，因此，基坑截渗墙外的来水量可近似采用公式(2)[15]计算，即为：

(2)

其中：

基坑内涌水量可依据文献[16]公式计算，即为：

(3)

其中：

根据水量平衡原理，基坑外侧的来水量应等于基坑内的涌水量，即为：

Q外=Q内

在式(2)及(3)中，如s0为已知，通过迭代法即可求得S，进而求得基坑的涌水量Q内(即为Q)。

2.3 约束条件

2.3.1 动力条件约束

基坑降水所需配套的动力(电力或机械功率)功率及基坑的涌水量应小于施工现场可以提供的动力功率及排水设施的排水能力，即：

或W≥R·Q

(4)

式中：N为施工现场可以提供的电力或动力条件，kW；Ni(i=1，2，3)分别为基坑降水、工程施工、生活及其它用电，kW；W为施工现场可以提供的设备排水能力，m3/d；R为安全备用系数，一般可取为1.1～1.2。

2.3.2 截渗墙深度施工条件约束

目前，用于防渗处理的截渗墙按其结构形式主要为垂直铺膜、深层搅拌、混凝土薄墙及高喷成墙等。各种成墙技术由于其施工工艺及机械设备条件限制，对成墙的地质岩性都有各自的适用条件，可成墙的最大深度也存在较大差异，因此，在进行截渗墙深度设计时，其最大截渗深度不能大于所选墙型的施工允许深度，即：

sf≥s=h1+H1+s0

(5)

式中：sf为与成墙型式及地层条件有关的允许成墙深度，m;s为自地面算起的墙体贯入深度，m;h1为地面至平均地下水位的高差，m。

2.3.3 周边环境条件约束

基坑降水将引起基坑周边地面不同程度的下沉，也因此可能引起这一区域内建筑物的不均匀下沉，直至引起建筑物工程发生破坏，因此，要求基坑周边地下水位的降落值应控制在一定范围，即：

hf≥h0

(6)

式中：hf、h0分别为基坑周边距基坑中心r处的地下水位允许下降值和实际降水值(h0可按《地下水动力学》的相关公式计算)，m。

2.3.4 防止管涌破坏约束

为防止基坑发生流沙及管涌现象，要求基坑内任一点的逸出水力坡降小于基坑土体的临界水力坡降；即：

J≤Jf

(7)

2.3.5 防止基坑底突涌约束

当基坑底部为承压含水层时，为防止基坑底发生突涌情况，要求坑底不透水层的厚度应满足式(8)：

(8)

式中：ht为基坑开挖后不透水层的厚度，m；γω、γ分别为水的重度及土的浮重度，kN/m3；hp为承压水头高于含水层顶板(基坑底)的高度，m。

2.3.6 防止发生潜蚀破坏约束

为防止基坑底发生潜蚀破坏，要求基坑内最不利点的逸出水力坡降满足式(9)要求：

J<(G0-1)(1-n)+0.5n

(9)

式中：J为基坑内最不利点的逸出水力坡降；G0为基坑底土体的比重；n为基坑底土体的空隙率。

2.3.7 防止发生流沙破坏约束

为防止基坑底发生流沙破坏，要满足2点要求。

(1) 基坑斜坡面应满足

对于无黏性土：

(10)

对于黏性土：

(11)

式中：φ为土的内摩擦角，(°)；c为土的粘聚力，kN/m2；θ为基坑边坡坡度，(°)。

(2) 基坑坑底应满足

对于无黏性土：

(12)

对于黏性土：

(13)

式中：γd为土的干重度，kN/m3。

2.3.8 截渗墙工期约束

截渗墙工程的实际施工工期应小于施工组织计划安排所要求的完工日期，即：

(14)

式中：W、WC分别为截渗墙的计划工期和实际工期，d；μ为截渗墙墙体单位平米的施工工期，d/m2；η为经验指数，一般为1～1.15。

3 数学模型的求解

3.1 模型的曲线特征分析

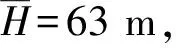
笔者分别完成了以下分析工作：① 当K=150及255 m/d时，基坑在无约束条件下，选取不同单价截渗墙情况下基坑控降水费用与截渗墙贯入深度的2组F(s)～s曲线，见图2、3所示；② 其他参数不变，当 150及255 m/d，控降水天数为120 d，基坑在无约束条件下，选取不同单价截渗墙情况下基坑控降水费用与截渗墙贯入深度的F(s)～s曲线，见图4、5所示。

由图2～5可见，因K、p及W的不同，F(s)～s曲线的类型也不同，按曲线的变化趋势主要可分3种类型，其特点是：

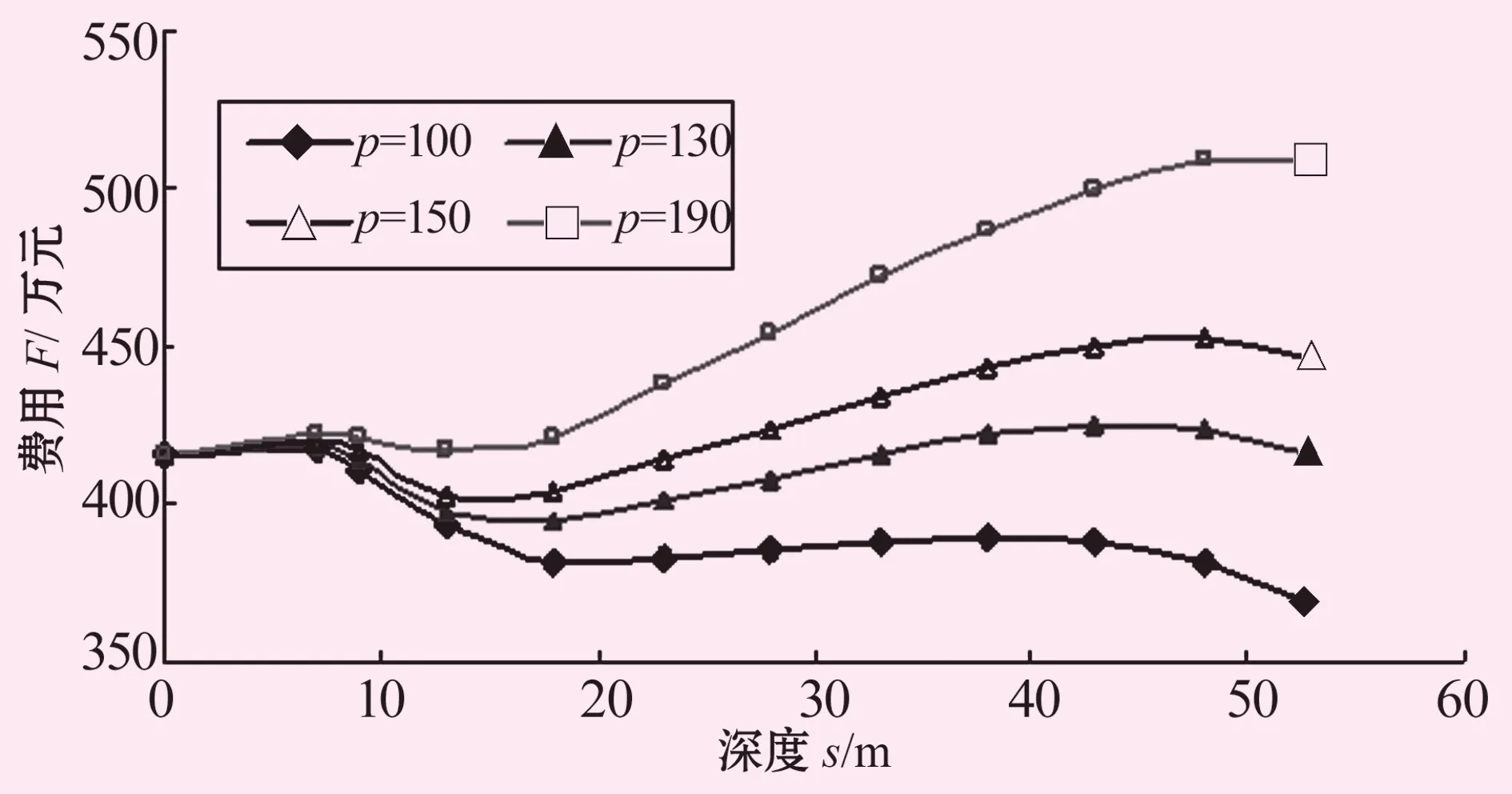
第1种类型为单峰型(如图2中的p=100、图3中的p=130及图5中的p=100曲线)。该种曲线显示：在截渗墙贯入深度s0较小的情况下(即s0sd时，基坑的控降水费用F(s)随截渗墙贯入深度的增加而减小，F(s)呈递减函数，并在截渗墙贯入深度达到不透水层时(全封闭式)，F(s)达到最小，如不计墙体及隔水层的渗入水量，F(s)≈minF(s)。

图2 s-F关系曲线(K=150 m/d)图

图3 s-F关系曲线(K=255 m/d)图

图4 控降水120 d的s-F关系曲线(K=150 m/d)图

图5 控降水120 d的s-F关系曲线(K=255 m/d)图

第3种类型为双峰递增型(如图2中的p=150、图3中的p=190及图5中的p=160曲线)。该类曲线的线型与第2类线型基本相同，所不同的是该曲线的趋势线为增函数型，且有minF(s)>F(0)关系。

由图2～4可见，随K的增大、优化墙型的p随之增加，表明最优墙型的选择范围更宽，通过设截渗墙降低基坑控降水费用的作用也更突出。比较图2、4及图3、5可见，在K及其他参数相同情况下，控降水时间T越长，通过设截渗墙降低基坑控降水费用的作用也越明显，反之，在控降水时间T相对较短情况下，选择设截渗墙降低基坑控降水费用意义不大，甚至没有可选择的优化墙型(如图4)。

3.2 最优墙体贯入深度求解

由前面对F(s)～s0曲线类型的分析可见，在满足相关约束条件下，第1类曲线类型为最经济墙型，可按该种墙体的最大成墙深度确定设计墙体贯入深度；第2类曲线类型为较经济墙型，应通过计算求解最优墙体贯入深度；第3种曲线类型为不合理墙型，应进行墙型调整。根据悬挂式截渗墙基坑控降水费用曲线的这些特点，最优墙体贯入深度的求解可按以下方法进行：

(1) 通过开展水文地质勘察获取工程基坑所在区域的水文地质参数及周边现有工程情况。根据基坑开挖施工组织设计分析计算基坑降水相关参数，并完成截渗墙工程的平面布置(尽量靠近基坑开挖边线，以有效减少基坑涌水量)，并初选拟建墙型。

(3) 根据《建筑基坑支护技术规程》[15]的相关公式，完成无截渗墙情况下基坑的降水总费用F(0)的计算，具体过程本文略。

(4) 当求得的最优贯入深度sa所对应的最小控降水费用minF(s)

4 工程实例

某橡胶坝枢纽船闸工程坐落于河滩地，地面高程145.50 m,施工期平均地下水位为143.50 m，隔水底板高程为86.50 m，基坑的平面开挖尺寸为110 m×45 m,基坑的控制水位为135.00 m。整个施工期各时段基坑的控降水位见表1所示，施工期的控降水天数为170 d。根据地勘成果经计算可得，含水层的加权平均渗透系数K=270 m/d。结合地质情况，拟采用高喷成墙工艺作为该水工建筑物基坑的截渗墙型式，设计成墙厚度为0.25 m ,经分析单位平米造价P=170元/m2。基坑降水统一采用6″离心泵明排，经分析在该基坑降水扬程范围内，单台水泵的排水流量为150 m3/(h·台),台时费用为β=55元/(h·台)。f=0.7万元，基坑周边无工程设施，在保证基坑开挖安全的情况下，试完成截渗墙的墙深设计。

表1 各施工时段基坑的控降水头表

利用本文公式及求解方法可得，该基坑截渗墙的最优贯入深度为地面以下21 m，其中，为节省工程投资，地面以下4 m不成墙(考虑墙外水位降深)，实际成墙高度为17 m。相应的基坑控降水总费用为649.8万元，较不设截渗墙基坑控降水总费用682.9节省费用33.1万元。

5 结语

本文采用常规的井流公式及阻力系数法，通过建立基坑内外水量平衡方程的形式，获得了悬挂式截渗墙贯入深度与基坑涌水量之间的计算公式，并以基坑控降水费用最小为优化目标，以基坑及周边工程安全为约束条件，给出了在已知基坑水文地质条件情况下确定悬挂式截渗墙墙体类型及墙体贯入深度的计算公式及获解方法，较好地解决了较深覆盖层基坑采用悬挂式截渗墙控降水的优化设计问题，避免了目前采用有限元及二维或三维数值模拟计算存在的诸多问题，计算过程简单直接，便于实际工程设计应用。

参考文献:

[1] 李永奎.北部引嫩泄洪闸工程围堰截渗施工技术探讨[J].水利建设与管理,2010,30(4)：28-30.

[2] 虎维岳.修正单纯形法及其在矿井疏干井群优化设计中的应用[J].工程勘察,1999,(2)：26-28.

[3] 王彩会.深基坑降水工程优化设计及渗流场与应力场耦合分析[D].南京:河海大学,2001.

[4] 刘志敏.水利基坑降水井群的优化方法和应用研究[D].南京:河海大学,2005.

[5] 徐岩,赵文,李慎刚.基于目标函数法的地铁隧道井群降水优化[J].水文地质工程地质,2009,36(5)：104-107

[6] 田春亮.深基坑降水井群优化设计及三维渗流有限元分析[D].西安:西安理工大学,2010.

[7] 滕凯,柳宝田,张永亮.基坑井群降水的优化[J].工程勘察,1995,(4)：33-36.

[8] 刘爱娟.基坑止水帷幕优化设计及工程应用[D].郑州:华北水利水电大学,2006.

[9] 何永福,朱进军，张雨花.深基坑止水帷幕的优化设计[J].常州工学院学报,2008,21(z1)：119-121.

[10] 王晓燕,党发宁,田威,等.大渡河某水电站围堰工程中悬挂式防渗墙深度的确定[J].岩土工程学报,2008,30(10)：1564-1568.

[11] 李存法,刘秀婷,从容,基坑截渗与降水工程优化设计方法浅析[J].地下水,2001,(3)：37-38.