基于标度因子的致密气藏压裂水平井产能分析

洪楚侨，张芨强，刘双琪，张风波，钟家峻，马帅

（中海石油（中国）有限公司湛江分公司，广东湛江524057）

基于标度因子的致密气藏压裂水平井产能分析

洪楚侨，张芨强，刘双琪，张风波，钟家峻，马帅

（中海石油（中国）有限公司湛江分公司，广东湛江524057）

致密气藏的储层物性差、自然产能低，水力压裂技术能较大地提高单井产量。针对水平井压裂后对气体渗流产生的影响，将地层中的流动划分为裂缝区域外的椭圆流动区以及裂缝区域内的线性流动区和径向流动区。以压裂水平井渗流原理为基础，运用多井干扰下的压降叠加原理和当量井径理论，引入标度因子和拟压力函数，建立了考虑应力敏感效应、气体滑脱效应和高速非达西效应的致密气藏压裂水平井产能计算模型。通过实例验证了模型在致密气藏压裂水平井产能预测方面的可靠性，并对诸多产能影响因素进行了敏感性分析。分析表明：气井产能与气体滑脱效应、裂缝半长、裂缝导流能力以及裂缝条数成正相关；在其他因素不变的情况下，存在一组最优的裂缝参数；应力敏感效应的存在会影响气井的产能，对生产造成一定的负面影响。

致密气藏；压裂水平井；标度因子；非达西流；产能分析

致密气藏的储层物性差，自然产能低，单井控制储量小，需要使用水力压裂等增产技术才能对其进行有效地开发。因此，针对水平井压裂后气体的渗流规律以及气井产能的研究就显得尤为重要。截至目前，国内外很多学者针对水平井压裂的具体情况，结合气藏流体的实际渗流规律，推导出了一系列关于压裂水平井产能的计算公式[1-9]。一些学者采用复位势理论和势的叠加原理，主要思路是将压裂水平井的渗流看成多条裂缝间相互干扰的问题，通过对各裂缝的势函数应用叠加原理进行求解。另外一些学者运用保角变换将裂缝引起的较为复杂的渗流问题简化为径向渗流或线性渗流等一系列更为常见的问题进行求解。还有一些学者基于椭圆流模型，运用发展矩形的思想，采用水电相似原理来描述流体在地层的渗流过程。然而，这样的求解思路太过陈旧，作出的简化太多，不能准确地描述流体在地下的真实流动情况。笔者充分考虑致密气藏的渗流特征，引入椭圆坐标系下的标度因子，运用压降叠加原理和当量井径理论，建立了考虑应力敏感效应、气体滑脱效应和高速非达西效应的致密气藏压裂水平井产能计算模型。通过实例计算，验证了模型的可靠性，并分析了各敏感因素对产能的影响，以期为致密气藏压裂水平井的产能分析提供新的思路。

1 物理模型

为方便研究压裂水平井在生产时引发的地层中流体的流动（图1），作出如下假设：①气藏顶底封闭，水平方向无限大，水平井为射孔完井；②水平井压裂后形成等长等间距分布的垂直裂缝；③裂缝完全穿透储层，即裂缝与气层厚度相等；④水平段无补孔，考虑裂缝间的干扰；⑤地层和裂缝中的流体为单相气体，渗流为等温稳态渗流，忽略重力、毛管力的影响；⑥由于水平井筒内的单相流体流动压力损失较小，因此考虑水平井筒为无限导流，水平井筒内的压力均相等。

图1 压裂水平井渗流物理模型Fig.1 Percolation physical model of fractured horizontal well

2 压裂水平井产能预测模型

根据假设条件以及建立的物理模型，将气体在气藏中的流动划分为两个区域和三个阶段。第一流动区域为气体在地层中的渗流，包括第一流动阶段的基质向裂缝的椭圆渗流。第二流动区域为气体在裂缝中的渗流，包括第二流动阶段裂缝尖端到近井筒段的线性流和第三流动阶段裂缝到井筒的径向流。

2.1 基质—裂缝流动

当水平井经过人工压裂生产后，气体在地层中的渗流方式会发生改变，从而诱发平面二维椭圆流（图2），即形成以裂缝端点为焦点的共轭等压椭圆和双曲线族[10]。

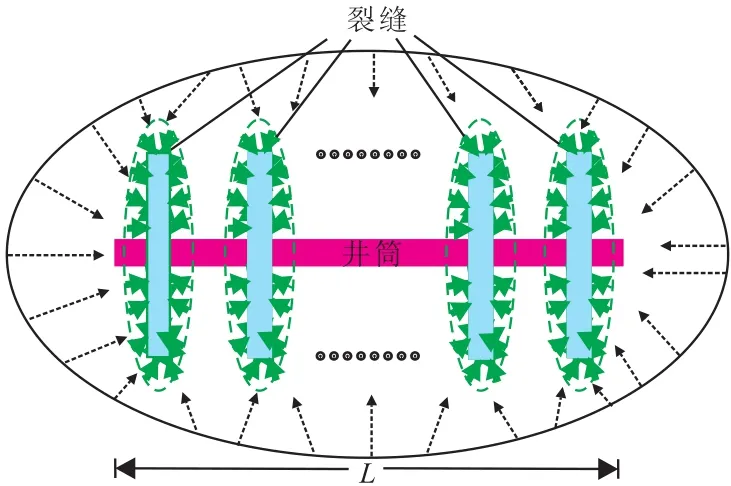
图2 基质—裂缝的椭圆流动Fig.2 Elliptical flow from matrix to fracture

由几何学知识可知直角坐标和椭圆坐标的关系（图3）为：

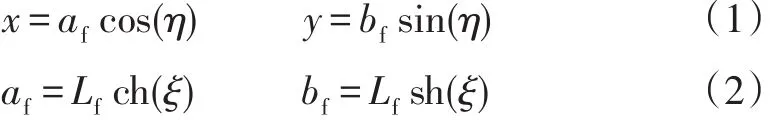
图3 直角坐标和椭圆坐标的关系Fig.3 Relation between rectangular and elliptic coordinates

式（1）～（2）中：x、y为直角坐标；η、ξ为椭圆坐标；af、bf分别为裂缝控制椭圆区域的长半轴、短半轴；cos(η)、sin(η)、ch(ξ)、sh(ξ)分别为η的余弦值、η的正弦值、ξ的双曲余弦值、ξ的双曲正弦值；Lf为裂缝半长，m。

气体在地层中渗流时，会受到滑脱效应[11]、应力敏感效应[12]的影响，其渗流数学模型由以下基本方程组成：

运动方程

地层应力敏感方程

滑脱效应方程

将式（4）～式（5）代入到式（3）中，可得：

式（6）中：v为气体渗流速度（地下），m/d；Kmo为原始地层渗透率，10-3μm2；b为气体滑脱因子，MPa；为地层与压裂水平井裂缝尖端中间区域的平均压力，MPa；αm为地层应力敏感系数，MPa-1；pi为原始地层压力，MPa；∇p为压力梯度，MPa/m；∇为哈密尔顿（Hamilton）算符；μ为气体黏度，mPa·s。

在椭圆坐标系中，哈密尔顿算符∇可以表示为：

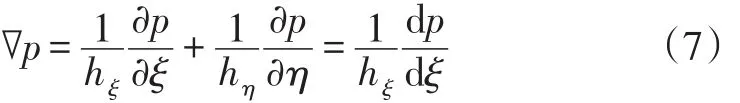
其中：hξ=hη=Lfsh2(ξ)+sin2(η)

式（7）中：hξ为椭圆坐标ξ的标度因子；hη为椭圆坐标η的标度因子。

将式（7）代入式（6）中，化简可得：

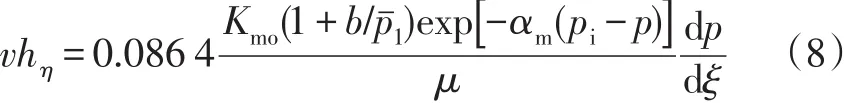
等式（8）两边同时对η在[0,2π]积分，得：

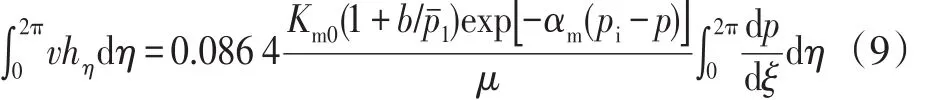
在椭圆坐标系下，地下体积流量、渗流面积和渗流速度的微分形式可表示为：

对式（10）两端进行积分，并将地下体积流量转化为地面产量，得：

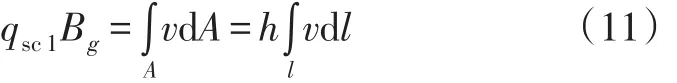
根据平面曲线弧长的定义，可以将椭圆的微元段弧长表示为：

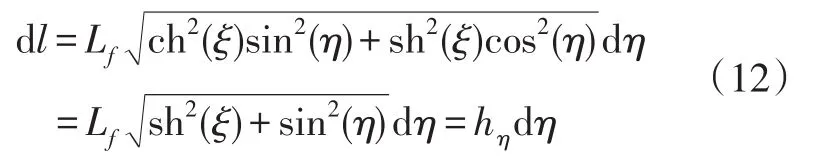
将式（12）带入式（11）中，可得：

联立式（9）和式（13），并引入气体体积系数Bg= ZTpsc/(pTsc)，化简可得：

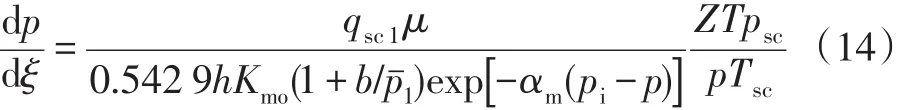
式（11）～（14）中：Z为气体偏差因子；T为气藏温度，K；psc为标准状态下压力，0.101 325 MPa；Tsc为标准状态下温度，293 K；A为渗流面积，m2；h为气层厚度，m；Bg为气体体积系数；qsc1为裂缝区域外的气体流量（地面），m3/d。

对式（14）两端的ξ和p同时积分，其中ξ从ξf到ξe，p从pf到pe。可得到地层中考虑滑脱效应和应力敏感效应的流动方程：

其中，ξe对应长半轴为供给半径re的椭圆，带入到式（2），有ξe=ch-1(re/Lf)。ξf对应平均短半轴为Wf/2的椭圆，根据相关学者的研究[13]，有

式（15）中：pf为裂缝尖端压力，MPa；ξe为椭圆坐标系下气藏外边界坐标；ξf为椭圆坐标系下裂缝尖端坐标。

2.2 裂缝—井筒流动

由于水平井形成的横向裂缝的横截面积远远大于水平井筒的横截面积（图4），所以气体会先从裂缝尖端以线性流形式流入到近井筒区域，然后发生汇流效应[14]，在近井筒区域形成径向流。综合考虑应力敏感效应、高速非达西效应[15]的裂缝渗流模型由以下几个方程组成。

高速紊流方程：

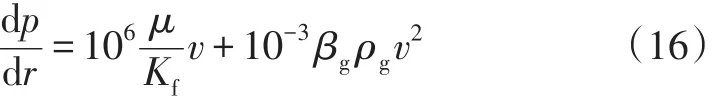
裂缝应力敏感方程：

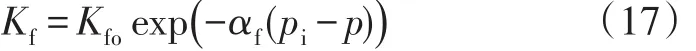
裂缝线性流动区的运动方程：

裂缝径向流动区的运动方程：

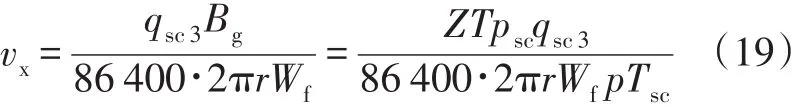
气体密度方程：

图4 气体在裂缝中渗流的物理模型Fig.4 The physical model of gas percolation in fractures

式（16）～（20）中：Kf为裂缝渗透率，10-3μm2；βg为气体紊流系数，m-1；ρg为气体密度，g/cm3；Kfo为裂缝原始压力下的渗透率，10-3μm2；αf为裂缝应力敏感系数，MPa-1；vl为气体在裂缝线性流动区的流速，m/d；qsc2为裂缝线性流动区气体流量（地面），m3/d；Wf为裂缝宽度，m；vx为气体在裂缝径向流动区的流速，m/d；qsc3为裂缝径向流动区气体流量（地面），m3/d；Mair为气体相对分子质量；γg为气体相对密度；R为摩尔气体常数，0.008 471 MPa·m3/(kmol·K)。

2.2.1 线性流动区

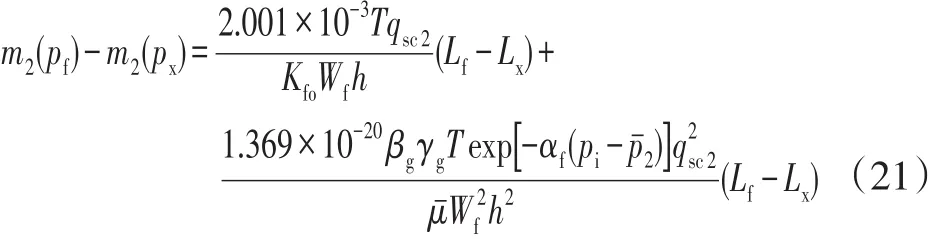
其中：Lx=h/2

式（21）中：px为裂缝内线性流动区和径向流动区（半径为rx）的交界面处的压力，MPa；为裂缝中线性流动区的平均压力，MPa；Lx为线性流动区和径向流动区交界面到井眼的距离，m。

2.2.2 径向流动区

气体在裂缝内的径向流（图4）等效于从圆形供给半径为rx，地层等效厚度为Wf的地层中向中心井径为rw的气井的流动。将式（17）、式（19）和式（20）带入式（16），并引入2.2.1节中定义的拟压力，经过积分化简可得裂缝中径向流动区考虑应力敏感效应和高速非达西效应的流动方程：

2.3 压裂水平井产能方程的建立

2.3.1 单条裂缝产能模型

根据气体流过的外部渗流场（地层中椭圆渗流）和内部渗流场（裂缝中线性流和径向流），运用水电相似原理（等值渗流阻力法）有qsc=qsc1=qsc2=qsc3，最后联立式（15）、式（21）、式（22）得到致密气藏有限导流压裂水平井单条裂缝产能方程：

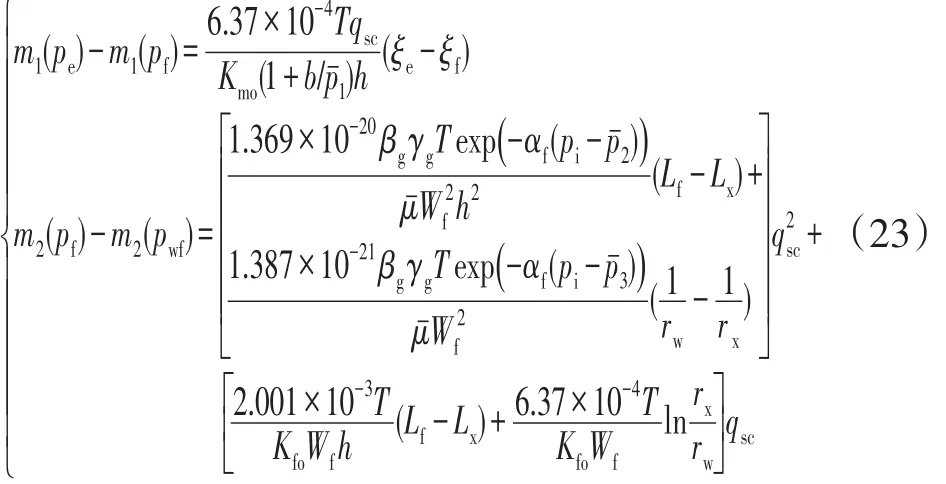
2.3.2 当量井径模型

为了更清晰地反映渗流原理，方便产能的计算，这里使用当量井径的概念[16]。根据广义达西方程、应力敏感和滑脱效应方程可得到常规达西渗流条件下考虑滑脱效应和应力敏感效应的普通直井产能方程：

将式（24）与单条裂缝产能公式（式（23））相比，产量相等时求得的直井井筒半径即为当量井径，用requ表示。

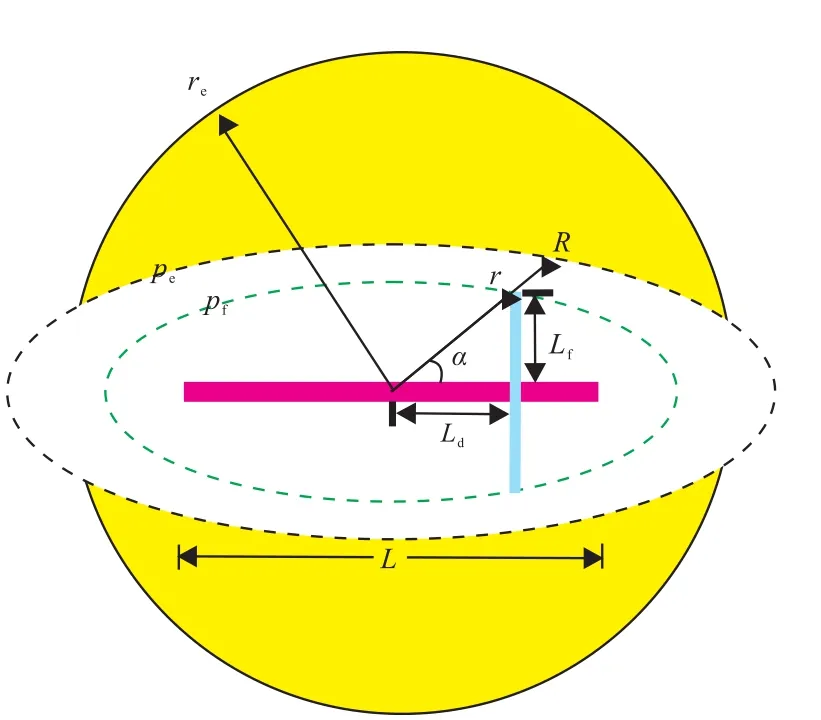
图5 压裂水平井渗流边界压力关系Fig.5 Percolation boundary pressure relation of fractured horizontal well

对于任一裂缝，假设沿着α角的压降成比例，由图5所示的几何关系，可知：

将式（28）稍作变形可得pf值：

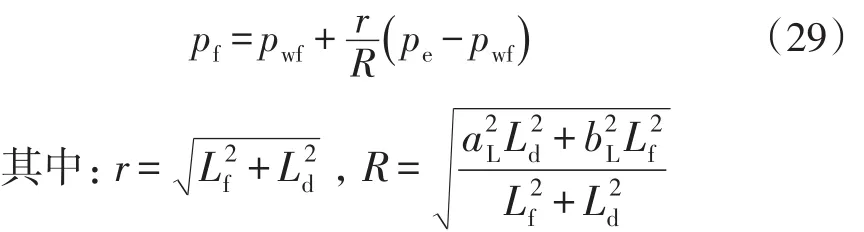
式（28）～（29）中：aL为水平井筒控制椭圆的长半轴，m；bL为水平井筒控制椭圆的短半轴，m；r为裂缝尖端到水平井筒中心的距离，m；α为水平井筒中心到任一裂缝尖端方向与水平井筒方向的夹角；R为α角下椭圆中心到椭圆边界的距离，m；Ld为任一裂缝到水平井筒中心的距离，m。

对于裂缝内线性流动区和径向流动区交界面处的压力值px，可联立线性流动区方程（21）和径向流动区方程（22），采用二分法得到。二分法是一种计算机算法，它的主要思路是从查值区间的两个端点逐步逼近函数零点的方法。

2.3.3 多条裂缝产能模型

压裂水平井有N条等长的横向裂缝，裂缝间距都为d，不同裂缝间存在相互干扰，且裂缝位置不同对整个生产的影响程度也不同。根据压降叠加理论，运用当量井径模型，将多裂缝水平井等效为多口直井，可得到每条裂缝处的拟压力降方程组的表达式：

由于不考虑井筒压降，井筒内压力处处相等，有pwf1=pwf2=pwf3=…=pwf，代入到线性方程组式（30）中，利用高斯消元法可求得各条裂缝的产量qsc1，qsc2，qsc3，…，qscn，那么压裂水平井总产量qsc=qsc1+qsc2+ qsc3+…+qscn。

3 实例分析

3.1 产能计算

为了提高经济效益，某致密气藏对水平井进行了水力压裂改造，根据相关的试气资料和试井解释资料，得到了气藏与水平井的基本参数如下：泄气半径re=520 m，原始地层压力pi=30.2 MPa，供给边界压力pe=28.3 MPa，地层温度T=364.4 K，原始地层渗透率Kmo=0.07×10-3μm2，气藏有效厚度h=12.2 m，地层渗透率变异系数αm=0.01 MPa-1，滑脱因子b=0.5 MPa，裂缝半长Lf=75.5 m，裂缝导流能力Kfo·Wf=255.5 10-3μm2·m，裂缝条数N=6，井筒半径rw=0.1 m，裂缝渗透率变异系数αk=0.07 MPa-1。

表1 产能评价结果Table 1 Productivity evaluation results

基于以上数据，计算出气井的无阻流量，并与修正等时试井以及试气得到的无阻流量进行对比，结果如表1所示。

从表1中的数据可以看出，理论公式的计算结果与修正等时试井结果比较接近，而与试气结果相差较大，说明理论计算公式具有一定的准确性和适用性。这是因为试气结果来自各气井完井后的试气地质报告，可靠性较差，而修正等时试井结果相对比较准确。

3.2 敏感性分析

为了进一步了解压裂水平井的产能，接下来分析应力敏感效应、气体滑脱效应、裂缝参数（裂缝半长、裂缝导流能力和裂缝条数）对压裂水平井产能的影响，这对致密气藏压裂水平井的开发有很重要的指导意义。

图6 不同地层渗透率变异系数下压裂水平井IPR曲线Fig.6 IPR curves of fractured horizontal wells under different formation permeability variation coefficients

图7 不同裂缝渗透率变异系数下压裂水平井IPR曲线Fig.7 IPR curves of fractured horizontal wells under different fracture permeability variation coefficients

1）应力敏感效应。应力敏感效应的存在会影响气井的产能，作出地层渗透率变异系数和裂缝渗透率变异系数影响下的压裂水平井IPR曲线，如图6～7所示。从图6～7中可以看出，气井产能与渗透率变异系数成负相关，这是因为渗透率变异系数越大，气体在渗流过程中的阻力越大，气井产能越小；裂缝渗透率变异系数对气井产能的影响比地层渗透率变异系数更大，这是由于裂缝中的应力敏感性比地层中更大，作影响因素分析时取值的范围更广。

2）气体滑脱效应。气体滑脱效应影响着气体在地层中的渗流，滑脱因子决定着其影响的强弱，如图8所示。从图中可以看出，随着滑脱因子的增大，气井产能也在逐渐增大，同时随着井底流压的降低，这种增大的趋势越发明显。说明滑脱效应会促进气体的流动，在气体的渗流过程中产生一种“附加动力”，同时这种“附加动力”的作用在井底流压较小的时候更加显著。

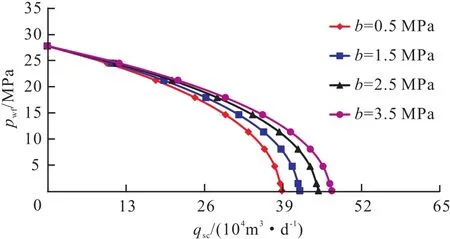
图8 不同滑脱因子下压裂水平井IPR曲线Fig.8 IPR curves of fractured horizontal wells under different slip factors

3）裂缝参数。裂缝半长、裂缝导流能力和裂缝条数是评价压裂效果的重要指标，作出相应的IPR曲线，如图9～11所示。从图9～11中可以看出，随着裂缝半长、裂缝导流能力和裂缝条数的增加，压裂水平井产能在不断增加，但增幅在逐渐变小。说明裂缝半长、裂缝导流能力和裂缝条数越大，气体流向井筒的流动通道越大，流动阻力越小，气井产能越大；存在一组最优的裂缝参数，应充分做好压裂施工规模设计。

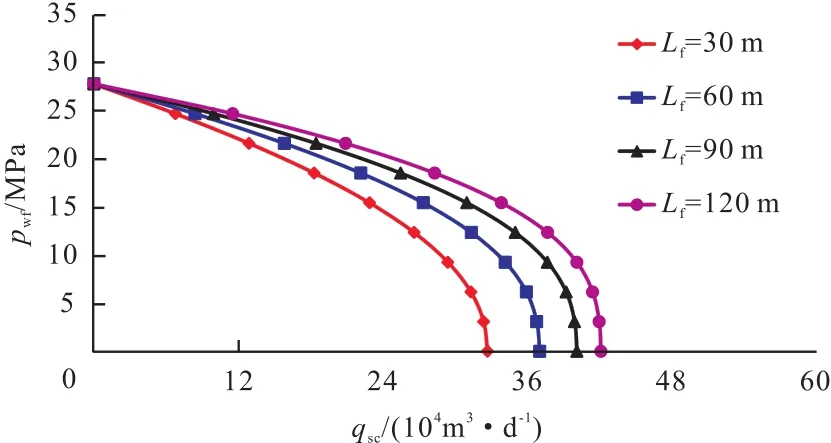
图9 不同裂缝半长下压裂水平井IPR曲线Fig.9 IPR curves of fractured horizontal wells under different fracture half lengths

图10 不同裂缝导流能力下压裂水平井IPR曲线Fig.10 IPR curves of fractured horizontal wells under different fracture flow conductivity

图11 不同裂缝条数下压裂水平井IPR曲线Fig.11 IPR curves of fractured horizontal wells under different fracture numbers

4 结论

1）在分析致密气藏渗流规律的基础上，运用多井干扰下势的叠加原理和当量井径理论，引入拟压力和椭圆坐标系下的标度因子，建立了考虑滑脱效应、应力敏感效应、高速非达西效应影响下的压裂水平井产能模型，并验证了模型的可靠性。

2）通过对应力敏感效应、气体滑脱效应，裂缝半长、裂缝导流能力和裂缝条数等因素的分析，得出气井产能与气体滑脱效应、裂缝半长、裂缝导流能力以及裂缝条数成正相关，在其他因素不变的情况下，存在一组最优的裂缝参数；应力敏感效应的存在会影响气井的产能，对其生产造成一定的负面影响。

[1]郎兆新，张丽华.压裂水平井产能研究[J].石油大学学报（自然科学版），1994，18（2）：43-46.

[2]生如岩，刘华，项希勇，等.致密气藏中压裂水平井的动态分析[J].油气地质与采收率，2003，10（1）：40-42.

[3]徐严波，齐桃，杨凤波，等.压裂后水平井产能预测新模型[J].石油学报，2006，27（1）：89-91,96.

[4]曾凡辉，郭建春，徐严波，等.压裂水平井产能影响因素[J].石油勘探与开发，2007，34（4）：474-477.

[5]王立军，张晓红，马宁，等.压裂水平井裂缝与井筒成任意角度时的产能预测模型[J].油气地质与采收率，2008，15（6）：73-75.

[6]魏建光，汪志明，张欣.裂缝参数对压裂水平井产能影响规律分析及重要性排序[J].水动力学研究与进展（A辑），2009，24（5）：631-639.

[7]汪志明，齐振林，魏建光，等.裂缝参数对压裂水平井入流动态的影响[J].中国石油大学学报（自然科学版），2010，34（1）：73-78.

[8]李勇明，李亚洲，赵金洲，等.压后水平气井生产动态预测模型[J].天然气工业，2012，32（9）：56-60.

[9]Hao M Q,Hu Y L,Liu X,et al.Predicting and optimizing the productivity of multiple transverse fractured horizontal wells in ultra-low permeability reservoirs[C]//International Petroleum Technology Conference,Beijing,China,2013：26-28.

[10]王强，童敏，武站国，等.致密气藏火山岩气藏压裂水平井产能预测方法[J].西南石油大学学报（自然科学版），2014，36（4）：107-115.

[11]Klinkenberg L J.The permeability of porous media to liquids and gases[C]//API Drilling and Production Practice,New York, USA,1941：200-213.

[12]George D V.Application of stress-dependent rock properties in reservoir studies[R].SPE 86979,2004.

[13]宋付权，刘慈群，张盛宗.低渗透油藏中水平井的产能公式分析[J].大庆石油地质与开发，1999，18（3）：33-35.

[14]郝明强，王晓冬，胡永乐.压敏性特低渗透油藏压裂水平井产能计算[J].中国石油大学学报（自然科学版），2012，35（6）：99-104.

[15]Forchheimer P.Wasserbewegung durch boden[J].Z.Ver. Deutsch.Ing.,1901,45(1)：1782-1788.

[16]魏漪，宋新民，冉启全，等.致密油藏压裂水平井非稳态产能预测模型[J].新疆石油地质，2014，35（1）：67-72.

[17]Yuan H,Zhou D.A new model for predicting inflow perfor⁃mance of fractured horizontal wells[C]//SPE Western Regional Meeting,Anaheim,California,USA,SPE 133610,2010.

（编辑：杨友胜）

Productivity analysis of fractured horizontal wells in tight gas reservoir based on scale factor

Hong Chuqiao,Zhang Jiqiang,Liu Shuangqi,Zhang Fengbo,Zhong Jiajun and Ma Shuai
(Zhanjiang Branch of CNOOC Co.,Ltd.,Zhanjiang,Guangdong 524057,China)

Due to poor reservoir properties and low natural productivity,hydraulic fracturing technology can greatly improve single well production.According to the impact of fractured horizontal wells on gas percolation,the flow in the formation can be divided in⁃to three parts,which include elliptical flow zone outside fractures,linear flow zone and radial flow zone inside fractures.Based on the percolation principle of fractured horizontal wells,by the adoption of pressure drawdown superposition and equivalent wellbore diameter theory,and through the introduction of scale factor and pseudo pressure,a productivity calculation model of the fractured horizontal well was established,which took into account stress sensitivity effect,slippage effect and high speed non-Darcy effect, furthermore,through examples of productivity prediction of fractured horizontal wells in tight gas reservoir,its reliability was veri⁃fied.Sensitivity analysis of production affecting factors shows that the productivity is positively related to slippage effect,fracture half length,fracture conductivity and fracture numbers,in addition,when other factors are unchanged,a set of optimal fracture pa⁃rameters can be obtained,and the stress sensitivity effects can affect gas well productivity and lead negative impacts on production.

tight gas reservoir,fractured horizontal well,scale factor,non-Darcy flow,productivity analysis

TE357.1

A

2015-07-24。

洪楚侨（1981—），男，工程师，油藏工程。

中国海洋石油总公司“十二五”科技重大项目（CNOOC-KJ 125 ZDXM 07 LTD 02 ZJ 11）。