铁路军事运输保障方案DEA评价
2015-05-09范灵毓
贺 强,刘 中,范灵毓
(1.军事交通学院 研究生管理大队,天津300161;2.军事交通学院联合投送系,天津300161)
快速准确地对铁路军事运输保障方案进行效能评价,对于帮助铁路沿线军代处及铁路部门科学合理使用保障资源、选择最佳保障方案、提高部队远程机动能力、高标准完成铁路军事运输保障任务具有重大现实意义。
1 DEA概述
数据包络分析(data envelopment analysis,DEA)是数学、运筹学、数理经济学和管理学科的一个新的交叉领域[1],它是以“相对概念”为基础,根据多指标投入和多指标产出对相同类型的单位进行相对有效性评价的一种系统分析方法[2]。将DEA方法应用于铁路军事运输保障方案评价领域有3种优势:一是可以对同类型的数个DEA单元即保障方案进行评价、排序和提供改进方向;二是DEA方法不直接作用于数值,因此无需对数据进行量纲化,利于提高评价的科学性;三是铁路军事运输保障方案评价体系相对庞大,利用DEA方法可以进行分割评价而又不失科学性。
2 DEA评价的一般步骤
将铁路军事运输保障方案抽象为一个具有有限个输入和输出的决策单元(DMU),选择恰当的DEA模型进行分析评价,具体流程如图1所示。

图1 DEA模型评价的具体流程
(1)确定评价目的。通过DEA的评价方法,科学合理地确定出同级的数个铁路军事运输保障方案中哪个方案最优,如何改进。
(2)选择DMU单元。DMU单元即是一个铁路军事运输保障方案,有多少个铁路军事运输保障方案就有多少个DMU评价单元,相互之间互不影响。
(3)评价指标体系建立。铁路军事运输保障方案的5大保障要素中对保障效能的影响程度由高到低依次为车辆保障、装卸站场保障、备品保障、运行保障和机车保障,本文以车辆保障(包括车流规律掌握指标、各型车辆保障数量指标、车辆整备集结时间指标、车辆不足加强指标)、装卸站场保障(包括固定设备保障指标、活动设备保障指标、人员保障能力指标、装卸能力预测指标)为例进行指标体系分析。
(4)DEA模型建立。假设有n个DMU,每个DMU都有m种投入和 s种产出。设 xij为第 j个DMU的第i种投入总量;yrj为第j个DMU的第r种产出总量;i=1,2,…,m;j=1,2,…,n;r=1,2,…,s。
各DMU的投入与产出用向量表示为Xj=
构造如下线性规划模型:

式中:λj(j=1,2,…,n)为 n个 DMU 的某种组合权重分别为按这种权重组合的虚构DMU的投入和产出量;和为所评价的第j0个DMU的投入和产出向量;V、θ为DEA的有效性值,最优值为1。
此线性规划的模型是找n个DMU的某种组合,使得其产出在不低于第j0个DMU的产出的条件下投入尽可能地减少[3-4]。
为了便于理解和计算,在此引入两个松弛变量S-(m维向量)、S+(s维向量)。因此,以上线性规划模型又可改进为

为了进一步简化模型求解,引入非阿基米德无穷小ε,ε是一个小于任何正数而大于零的数。于是,模型变换为

(5)DEA评价并得出结论。利用单纯形方法、Matlab和lingo方法求得模型的最优解:λ*、S*-、S*+、θ*。①如果θ*=1,则第j0个DMU为弱DEA有效,即第j0个运输保障方案不好;②如果θ*=1且S*-=0,S*+=0,则第j0个DMU为DEA有效,即第j0个运输保障方案好;③如果θ*≠1,其中θ*值越小,相对有效性越差,即运输保障方案越不可靠。
3 实例验证
为了验证DEA方法在评价中的效用,选择了某部队一次铁路军事运输行动中保障任务的3套保障方案进行验证(方案2、方案3为备用方案)。X为输入变量,Y为输出变量:

式中:i⊆(1,2,3,4,5,6,7,8);r⊆(1,2);j⊆(1,2,3)。
由于该评价体系中,车流规律掌握指标、固定设备保障指标、活动设备保障指标、人员保障能力指标、装卸能力预测指标为定性指标,采用专家打分法对其进行量化。各型车辆保障数量指标、车辆整备保障数量指标、车辆不足加强指标为定量指标,可直接由保障方案得出。
在对定性指标进行量化时,我们邀请了具备丰富铁路军事运输保障经验、铁路局等有关专家学者共10人,分别对3套保障方案中每个定性指标进行了逐一打分(10分制),并对同一指标不同专家的打分情况进行了方差估计(允许误差δ≤0.001),对于方差 δ>0.001的指标进行重新打分,直至δ≤0.001方可,由此得出铁路军事运输保障方案评价指标量化值(见表1)。
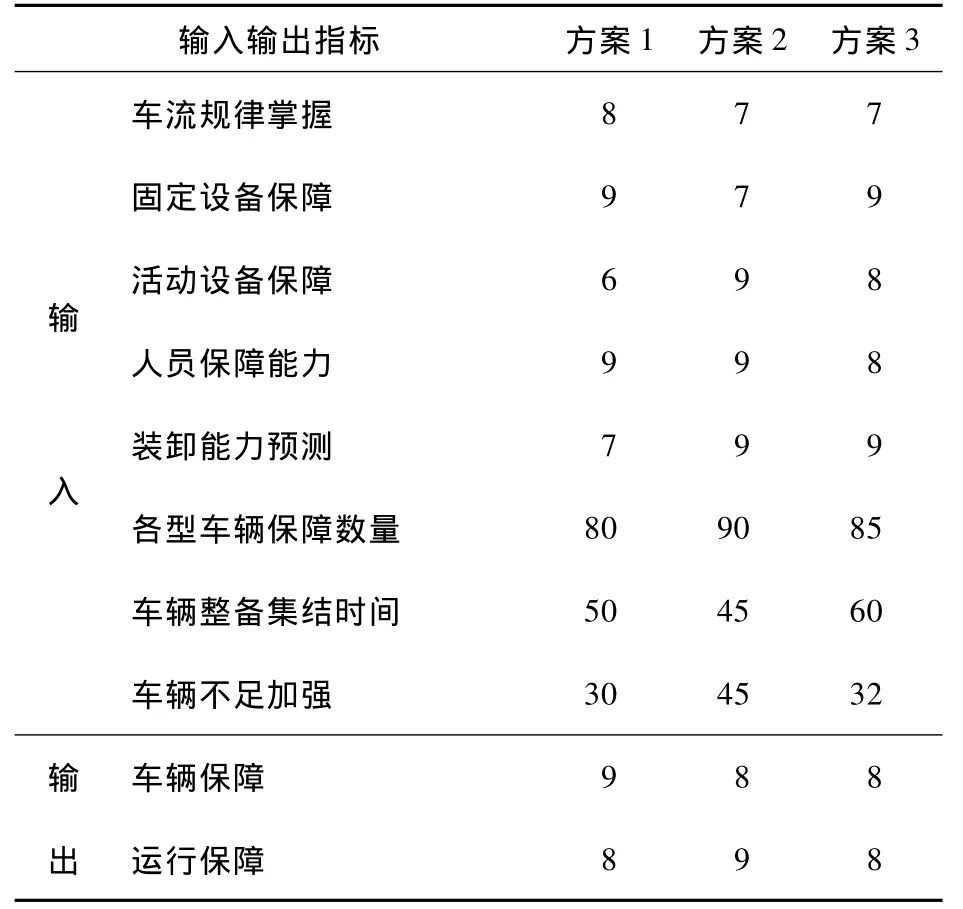
表1 铁路军事运输保障方案评价指标量化值
采用DEA评价方法,建立模型如下。
方案1:

方案2:

方案3:
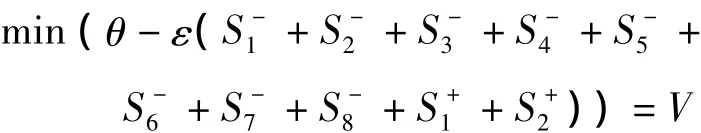

利用Lingo软件对以上3个模型进行求解,结果见表2。
由以上计算结果可得出如下结论:方案3相对有效性最差,方案1和方案2都是弱DEA有效。
4 结语
以上采用DEA评价方法对3套铁路军事运输保障方案进行了评价,将所述评价标准与Lingo计算结果进行综合分析,发现:
方案1 和方案 2 中,θ*=1,S*+=0,S*-不全为0,说明方案1和方案2实际保障效能较好,能够完成既定铁路军事运输保障任务。方案3,θ*≠1,S*+、S*-不全为 0,说明方案实际保障效能最差,很难满足既定铁路军事运输保障任务。
实际中,分别将3套保障方案提交给了不同的专家评审,最终选择运用了方案1,保障任务总体完成得比较好,这与DEA评价方法结果显示一致,说明该评价方法具有较强的实用性和科学性。
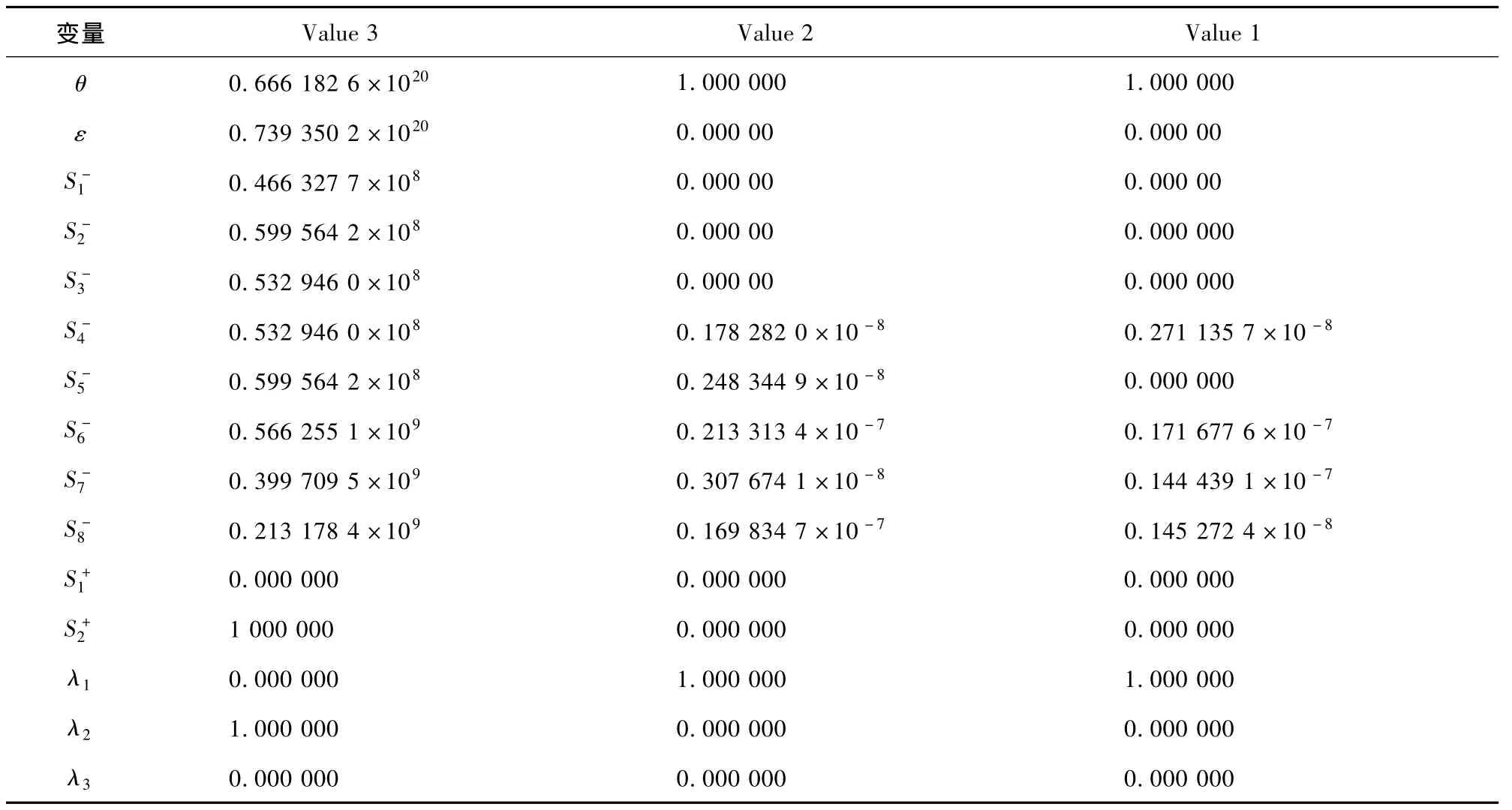
表2 利用Lingo软件对3个模型求解结果
[1] 魏权龄.数据包络分析[M].北京:科学出版社,2006:3-4.
[2] 盛昭翰.DEA理论、方法与应用[M].北京:科学出版社,1996:5-6.
[3] 曲丽丽,康锐.基于DEA的研制阶段装备保障方案评价模型[J].指挥控制与仿真,2011,33(3):57-60.
[4] 李美娟,陈国宏.数据包络分析法(DEA)的研究与应用[J].中国工程科学,2003,5(6):88-90.
