求解微分方程的电路设计

孔 特，魏建成，陈琳洛，邹 京， 吴援明

(电子科技大学 光电信息学院，成都 610054)

求解微分方程的电路设计

孔 特，魏建成，陈琳洛，邹 京， 吴援明

(电子科技大学 光电信息学院，成都 610054)

电子电路的物理特性使其能够让人避开烦琐的数学方法而快速求解微分方程。文中从非数学手段的方面去分析二阶微分方程的解决方法，将其转化成电路设计的形式。通过一个具体的二阶微分方程，设计出相应电路，并且通过计算机仿真软件测试了设计电路。针对仿真结果暴露出的几个问题，改进了电路，且在改进的电路上总结归纳出了电路设计的几点要求。在此基础上，进一步构建出适解一切二阶微分方程的电路模型，并给出了电路中元器件参数的设计要求。

解微分方程；集成运算放大器；积分电路；计算机模拟

1 设计目标与设计思路

1.1 设计目标

对二阶微分方程， 通常通过一系列的数学手段来解决。若可运用集成电路搭建积分电路的功能，将会是一种解决二阶微分方程更加便捷的方法。本文探究和设计一种能够解决二阶微分方程的电路。

1.2 设计思路

1.2.1 求解微分方程思路的理论分析

设一个一般的二阶微分方程：

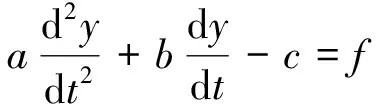
(1)

对式(1)做移项处理得：

(2)

再对式(2)左右两边做一次积分处理得：

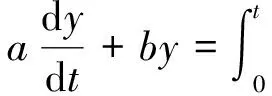
(3)

分析式(3)，在电子电路的设计上，这一步积分可理解为将信号c和信号f(t)送入一个积分电路(设为第一级积分电路)。

继续对式(3)再做一次移项，使等式的左边始终保持只有微分项。令：

(4)

对式(4)左右两边再做一次积分，得：

(5)

从式(5)可以看出，我们成功解出了y。在电子电路的设计上，这一步可理解为将第一级积分电路的输出和第二级积分电路的输出的b倍，输入到第二级积分电路的输入端。

综合上述分析，整个解决二阶微分方程的电路需要两级积分电路，其中第一级积分电路输入端有两个输入，分别为常量c和获取信号f(x)。故可使用集成运放搭建单项积分电路作为电路的第一级，第一级的输出即为Z1，搭建一个两项加法电路作为电路的第二级，其中两个输入为Z1和by。

1.2.2 电路设计的理论分析

由模拟电路的相关知识知，通过一个集成运放和相关的外围电路构成一个积分电路，如图1所示。

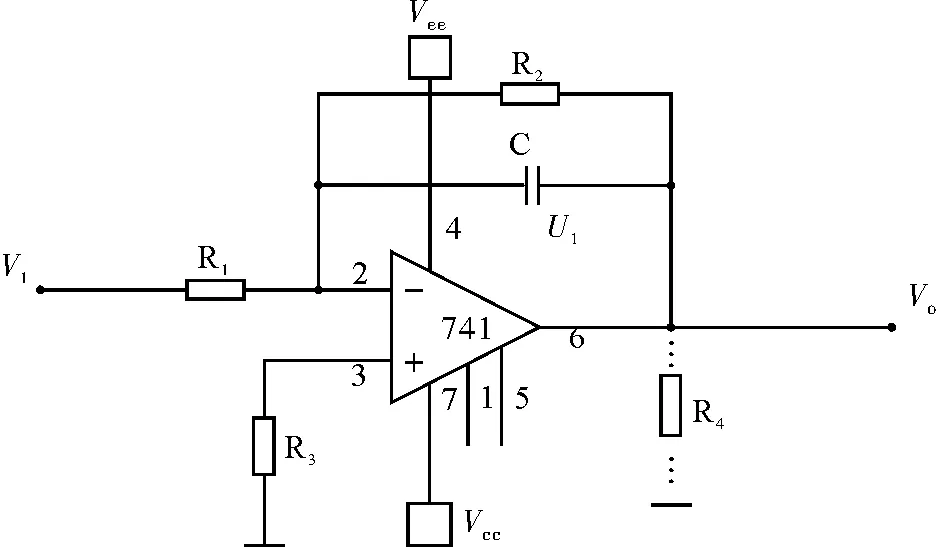
图1 集成运放构建的简单积分电路

由虚短、虚断的概念和电容的伏安关系可得：

式中：Vo(t)表示积分电路的输出；Vi(t)表示积分电路的输入信号；Vc(0)是电容上的初值电压；R1C即为图1中电阻R1与电容C的乘积。由输入、输出关系可知，可以通过R1和C两个元件来控制积分中的系数[3]。

2 设计步骤及仿真

2.1 设计步骤

为方便起见，我们将以

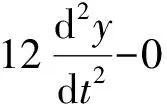
为特例，通过上文的设计思路设计一个能够解决该微分方程的电路，借助Multisim电路仿真模拟软件进行仿真验证。根据之前的设计思路，对式(3)的分析可知，我们需要将信号c和信号f(t)送入一个积分电路，因为式中无直流信号c，所以输入只有一个f(t)。选用1.2.2中所设计的积分电路，该电路即为第一级积分电路。

第一级积分电路的元器件及参数设置如下：选用OPAMP741集成运放，2脚连的输入电阻R1选择50kΩ，3脚连的接地电阻Re1选择10kΩ，反馈电容选择0.2μF。再对式(5)的分析可知，电路的第二级积分电路需要两个输入Z1和-by，故对第二级积分电路做双输入处理。

第二级积分电路的元器件及参数设置如下：选用OPAMP741集成运放，2脚第一个输入是来自第一级积分电路的输出，其输入电阻R2选择5kΩ，第二个输入来自第二级积分电路的输出，其输入电阻选择120kΩ，反馈电容选择0.2μF，3脚的接地电阻Re2选择10kΩ。

将两级积分电路连接就得到了解决所给的特例微分方程的电路，设计好的积分电路如图2所示。

图2 初次构建求解微分方程的电路图

2.2 仿真测试

经由2.1节的设计，电路的主体部分已经搭建好。接上直流电源，再由函数发生器产生频率50 Hz、振幅500 mV的正弦信号作为测试信号，检验搭建的电路是否满足微分方程的理论解：

仿真结果显示，第一级积分电路和第二级积分电路的输出都有明显的失真(对输出信号使用了示波器的交流档，只显示了输出信号交流部分的波形)，使用探针测试输出端的电压、电流参数，探针测试结果表明，输出具有严重的直流偏移现象，Vdc=-14.1 V。这次仿真结果并没有达到要求，如图3所示。

3 关键问题与改进方法

3.1 问题发现

根据以上的测试结果，电路输出存在两个关键问题：(1)电路的输出存在直流偏移现象；(2)输出的波形存在失真情况。

3.2 改进方法

针对电路输出波形失真情况，可采用在反馈电容上并联一个数值合适的电阻来解决。通过不断改

图3 初次测试的输入与输出波形

变3脚上的接地电阻的阻值大小来调节直流偏移[3]。

结合以上改进，我们决定在两级电路的反馈电容上各自并联一个200 kΩ的电阻。同时，调节第一级积分电路的接地电阻为80 kΩ左右，调节第二级积分电路的接地电阻为75 kΩ左右。

3.3 再次仿真

再次仿真结果表明，在之前仿真中出现的问题得到了较好的解决，电路的直流偏移现象基本消除，波形的失真现象也得到了很好的解决，如图4所示。

图4 改进电路之后测试的输入与输出波形

3.4 电路改进测试

虽然上次的电路改进基本解决了失真和直流偏移问题，但是电路从开始运行到达到稳态需要较长的时间，即电路的响应比较慢，延迟比较严重。

为了使电路的响应变快，需要减小电路的时间常数，即R、C的乘积值。将电容值改为原值的1/10，再次测试发现电路又出现了失真，可知，电路的时间常数不能任意减小，所以电容、电阻选择具有一定的范围。超出一定范围可能会使电路不能工作在正常状态。本次试验选的电阻、电容值已在合理范围内，故不再做改动。

4 结束语

通过求解12(d2y/dt2)-0.5(dy/dt)=f(t)的电子电路的设计，已经证实上文关于求解二阶微分方程电路的设计分析是合理的，通过两级积分电路确实能够解决二阶微分方程。对于一般的微分方程a(d2y/dt2)+b(dy/dt)+c=f(t)，该两级积分电路一般具有如图5所示的电路结构。

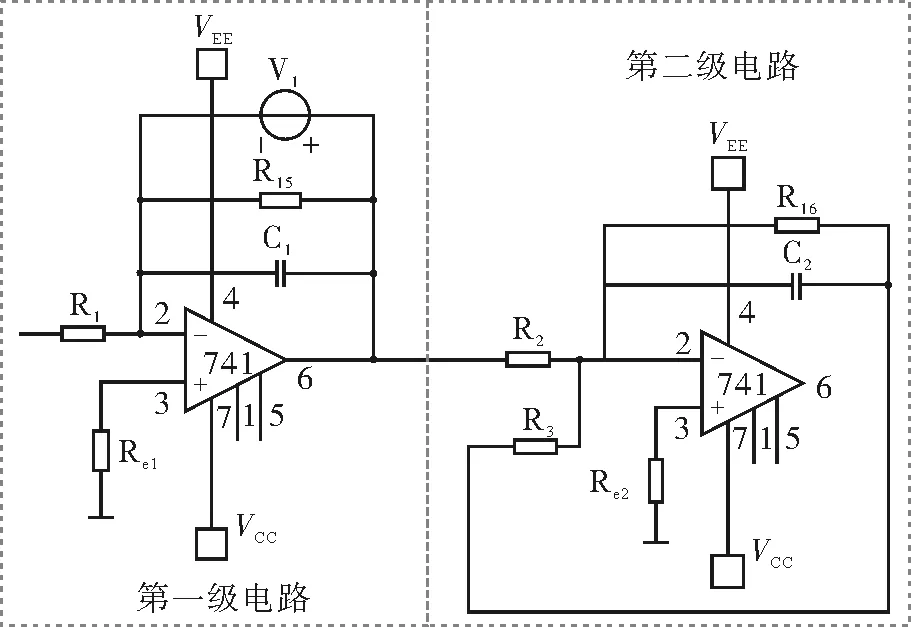
图5 求解二阶微分方程的电路模型

第一级电路中的R1C1的数值应该等于1左右(合理的数量级应该在10-2上)，并联在电容上的直流电源为电容提供初始值(初始值为0时，可去除这个直流电源)。3脚上的接地电阻具有调节电路输出的直流偏移的作用，并联在电容上的电阻具有稳定电路输出、调节失真的作用。这两者都要在电路中调节不同的值。第二级积分电路中R2C2的数值上应该等于1/a(合理的数量级在10-2上)；R3C3的数值上应等于b/a(合理的数量级在10-2上)；至于3脚上的接地电容和并联在电容上的电阻的作用同第一级的一样(效果作用于第二级电路上)[4]。

除此之外，积分电路利用了电容的记忆性，所以，在设计电路时，考虑到电容大小对电路的影响。首先，输入信号的频率必须满足f>1/(2πR1C)，否则起不到积分作用；其次，电容的选取不能太小，电容过小容易导致出现饱和的情况，导致输出的波形有所缺失。选取电容的时候，尽量选取容值较小的电容、大电阻，使得电路的输入电流较小。

[1]施学东.求解微分方程的一种简明方法[EB/OL].[2013.12.17].http://www.cnki.com.cn/Article/CJFDTotal-XYSK198904004.htm.

[2]吴援明，唐军.模拟电路分析与设计基础[M].北京:科学出版社，2006:387-388.

[3]吴援明，唐军，曲健.模拟电路分析与设计基础学习指导[M].北京:科学出版社，2007:202-203.

[4]崔红玲，李朝海，陈骏莲， 等.电子技术基础实验[M].成都:电子科技大学出版社，2008:166-167.

Circuit Design of Solving Differential Equation

KONG Te, WEI Jiancheng, CHEN Linluo, ZOU Jing, WU Yuanmin

(School of Optoelectronic Information, University of Electronic Science and Technology of China, Chengdu 610054, China)

The physical properties of electronic circuit can make people avoid using the tedious mathematical methods,and solve the differential equation more easily. In consideration of these advantages of electronic circuit, the following text will analyze the methods to solve second-order differential equation from the aspects of non-mathematical methods, and convert it to the form of circuit design. Through a concrete second-order differential equation, we can design the corresponding circuit, and test the designed circuit through computer simulation software. According to a few questions revealing from simulation results, we modify the circuit accordingly, and summarize the several requirements of circuit design in the modified circuit. On these basis, we can build a circuit model available to all of second-order differential equation further, as well as the design requirements of circuit components parameters.

solving differential equations；integrated operational amplifier；integrator circuits；computer simulation

2014-04-08；修改日期: 2014-12-23

孔 特(1994-)，男，本科在读，专业:信息显示与光电技术。

吴援明(1966-)，男，教授，研究方向：光电信息处理。

TM

Bdoi:10.3969/j.issn.1672-4550.2015.04.066