改进求解Woods-Saxon 势 和Pöschl-Teller 势的方法

郝海玲， 闫景富

(1.晋中职业技术学院 基础部，山西 晋中 030600；2.中国石油大学(北京) 信息学院，北京 102249)

改进求解Woods-Saxon 势 和Pöschl-Teller 势的方法

郝海玲1， 闫景富2

(1.晋中职业技术学院 基础部，山西 晋中 030600；2.中国石油大学(北京) 信息学院，北京 102249)

用Wang的Obrechkoff数值方法来求解常见的Schrödinger方程，即两步高阶微商。该方法的特点是采用增加奇数高阶微商使得数值结果P稳定。Schrödinger方程中，例如一维的 Woods-Saxon势和Pöschl-Teller势，使用该方法计算后，不仅提高了计算效率，也提高了数值结果的精度。

P稳定；Obrechkoff 方法；Woods-Saxon势；Pöschl-Teller势

根据Wang的多步方法稳定性理论，把原来具有较高精度的含有偶数阶微商的P稳定两步方法进行改进，即在增加奇数阶微商后变成连续阶高阶微商，从而在数值结果上提高了精度，提高了效率。这种方法叫做P稳定两步Obrechkoff方法[1-4]。本文利用该方法数值求解一维Schrödinger方程能量本征值，例如，常见的Morse势[5-6]、Woods-Saxon势[7]和Pöschl-Teller势[8-9]，着重计算后两个方程。计算结果显示了该方法的数值结果在效率和精度上的优越性。

1 方法介绍

Wang的经典两步Obrechkoff方法使用偶数阶微商，而P稳定两步Obrechkoff方法使用连续阶高阶微商，即两边增加奇数阶微商，其结构可以表示为

y(x+h)+y(x-h)+c0y(x)=

h(c1(y′(x+h)-y′(x-h)))+

h2(c2(y″(x+h)+y″(x-h))+

c3y″(x))+h3(c4(y(3)(x+h)-

y(3)(x-h)))+h4(c5(y(4)(x+h)+

y(4)(x-h))+c6y(4)(x))+

h5(c7(y(5)(x+h)-y(5)(x-h)))+

h6(c8(y(6)(x+h)+

y(6)(x-h))+c9y(6)(x))

(1)

比较两种方法，使用连续阶微商的新方法的截断误差及其系数都要远远小于经典方法。所以，可以认为新的Obrechkoff两步方法具有很高的精度。

另外，新方法的稳定性也优于经典方法，并且是利用三角拟合方法得到的P稳定的Obrechkoff两步方法[9]。

2 实例求解

本文将用两种一维Schrödinger方程作为例子来检验新的Obrechkoff两步方法的精度和效率。第一个实例是求解Woods-Saxon势的束缚态和共振态的能量本征值；第二个实例是求解Pöschl-Teller势的束缚态能量。

计算机标准为16位精度，因此计算程序选用Mathematica高精度进行编制。

2.1 Woods-Saxon势

Woods-Saxon势是原子核中核子(包括原子和中子)的中心势场，在原子结构的研究中占有重要地位。这个势用来近似地描述原子核模型中每一个核子的势能函数，因此，表示每个距离核中心为x的点的核子势能可表示如下

v(x)=c0z[1-a(1-z)]

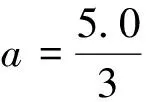
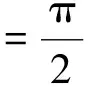
在这里，我们进行两种方法的比较。束缚态和共振态的初值(ψ(0)，ψ′(0))为(0，h)，那么(ψ(h)，ψ′(h))用单步Obrechkoff方法计算[11]，依次迭代得到束缚态波函数ψ(xmax)和共振态δ(Es)。ψ(xmax)是关于束缚态本征值Es的函数，共振态波函数利用δ(Es)表达如下

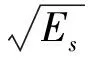
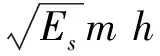
通过编程计算，我们得到的束缚态本征值的数值结果，用图形表示，如图1和图2所示。

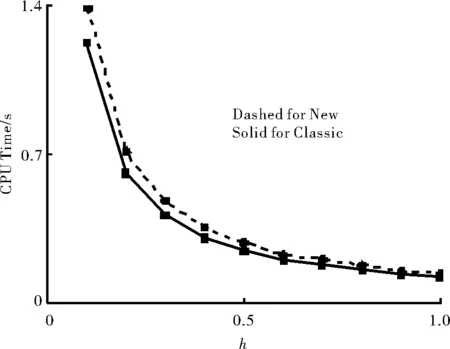
图1 两种方法计算束缚态本征值的CPU时间比较

图2 两种方法在步长取1/10和1/15的ΔE比较

从图2可以看出，当步长较大时，计算机计算比较复杂，所用的CPU时间就少。其中ΔE=Es-Esi，Esi的选取参考文献[9]。新方法和经典方法的主结构的最高阶微商都是6阶，而初值的单步Obrechkoff方法分别选取了6阶和9阶，可见，在选取相同步长和相同初值的情况下，新方法的精度明显高于经典方法。再者，从图1中可以看出，相同步长时新方法和经典方法的时间基本相同。这样，我们可以判断出，如果用两种方法求解同一方程，取相同的步长，要想达到同样精度的结果，新方法计算的CPU时间明显少于经典方法。因此，可以说新方法比经典方法效率高。从这点可以看出，新方法比经典方法更加有效。

共振态本征值的数值结果如图3和图4所示，其中，ΔE=Es-Esi。同理，新方法的主结构和初值的方法都与求束缚态的方法相同，同样步长情况下，新方法的精度明显高于经典方法。可以得出，在求解共振态时间效率和精度方面，新方法仍然优于经典方法。

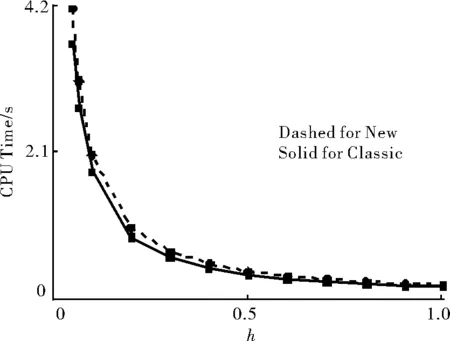
图3 两种方法计算共振态的CPU时间比较

图4 两种方法在步长取1/10和1/30时ΔE的比较

2.2Pöschl-Teller势

Pöschl-Teller势是用来描述非线性光学性能的势函数。其函数形式如下

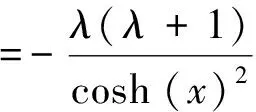
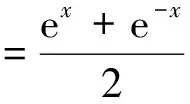
Pöschl-Teller势也是一个势阱，类似于谐振子。我们的任务同样是找到它的束缚态的能量本征值，而且通过解析解可以看出它的波函数图形也与一维谐振子类似。一维Pöschl-Teller势的Schrödinger方程为

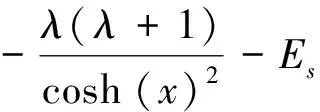
那么，我们计算上式的20个能量本征值，其解析解为

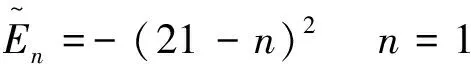
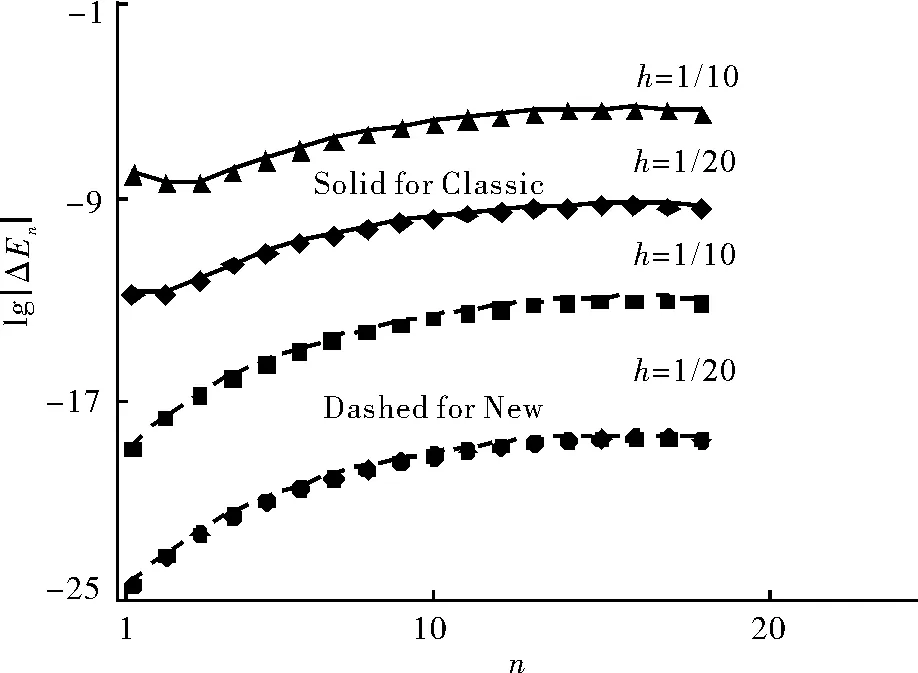
图5 两种方法在步长分别取1/10和1/20时ΔE的比较

图6 两种方法在步长分别取1/15和1/30时ΔE的比较

3 结束语

利用P稳定两步Obrechkoff方法求解Woods-Saxon势和Pöschl-Teller势能量本征值，验证了其是一种高效率、高精度且稳定性比较好的数值方法。对于求解一维Schrödinger方程的本征值问题，该方法具有很大的优越性。

[1]WangZ，DaiY.Atwelfth-orderfour-stepformulaforthenumericalintegrationoftheone-dimensionalSchrödingerequation[J].Int.J.Mord.Phys.C.， 2003(14)：1087-1105.

[2]WangZ，DaiY.Aneighth-ordertwo-stepformulaforthenumericalintegrationoftheone-dimensionalSchrödingerequation[J].N.Math.J.Chin.Univ.， 2003(12)：146-150.

[3]WangZ，GeY，DaiY，etal.Amathematicaprogramforthetwo-steptwelfth-ordermethodwithmulti-derivativeforthenumericalsolutionofanone-dimensionalSchrödingerequation[J].Comput.Phys.Commun.， 2004， 160：23-45.

[4]郝海玲.求解一维Schrödinger方程的P稳定两步Obrechkoff方法[J].上海大学学报：自然科学版，2010，16(1):53-57.

[5]RankDH，EastmanDP，RaoBS，etal.Breadthsandshiftsofmolecularbandlinesduetoperturbationbyforeigngases[J].JournalofMolecularSpectroscopy， 1963(10)34-50.

[6]LambetJD.Symmetricmultistepmethodsforperiodicinitialvalueproblems[J].J.Inst.Math.Appl.， 1976(18)：189-202.

[7]Wang Zhongcheng. A new effective algorithm for the resonant state of a Schrödinger equation[J]. Computer Physics Communications，2005(1)：1-6.

[8]Wang Z， Dai Y.An eighth-order two-step formula for the numerical integration of the one-dimensional Schrödinger equation[J]. N. Math. J. Chin. Univ.， 2003(12):146-150.

[9] Wang Zhongcheng.P-stable linear symmetric multistep methods for periodic initial-value problems[J].Comput.Phys.Commun.，2005，171:162-174.

Method for the Woods-Saxon Potential and Pöschl-Teller Potential

HAO Hailing1，YAN Jingfu2

(1.Department of Foundation , Jinzhong Vocational Technical College, Jinzhong 030600, China;2. School of Information,China University of Petroleum - Beijing, Beijing 102249, China)

In this paper, we focus on the new kind of P-stable two-step Obrechkoff method for the ultra-high-accurate solution of a one-dimensional Schrödinger equation.Through improving the Wang’s method, we develop a new kind of P-stable two-step Obrechkoff method by adding the odd higher-order derivatives. This proposed method is very effective but has very high local truncation error. We apply our new method to the one-dimensional Schrödinger equation such as the well-know Woods-Saxon potential and Pöschl-Teller potential. Their numerical solution testified that the new method is very reliability.

P-stable；Obrechkoff method；Woods-Saxon potential；Pöschl-Teller potential

2014-09-19；修改日期: 2014-11-06

郝海玲(1979- )，女，硕士，讲师，研究方向：物理问题的数值解法。

O411

A

10.3969/j.issn.1672-4550.2015.04.006