状态反馈在随动系统设计中的应用

尚亚锐，王 斌

(西北工业大学 明德学院， 西安 710124)

状态反馈在随动系统设计中的应用

尚亚锐，王 斌

(西北工业大学 明德学院， 西安 710124)

文中采用状态反馈对任意配置极点的随动系统进行了设计、仿真和模拟调试。其中包括随动系统传递函数的辨识、状态空间表达式的建立、状态反馈系数矩阵的计算、系统Simulink仿真研究以及模拟调试。研究了状态反馈系统加死区特性、饱和特性及干扰特性的输出响应曲线，通过曲线分析最终证明状态反馈系统响应速度快、稳定性好、抗干扰能力强。该系统参数调试简单、电路便于实现，为随动系统的实现找到了一个新途径。

状态反馈；随动系统；Simulink仿真；模拟调试

1 广义对象状态空间表达式

1.1 广义对象时间响应特性测试和传递函数辨识

将3 V阶跃信号电压加于功率放大器输入端，分别测出电动机电枢电流、输出转速和位移经变换后的各直流电压的时间特性曲线，根据响应特性特点：单调变化且电流转速有稳态值，可采用(t1，0.4c(∞))， (t2，0.8c(∞))两点法来辨识其传递函数[1]。

1)对电流：t1=0.07s，t2=0.45s，辨识出

2)对转速：t1=0.239s，tz=0.550s，辨识出

3)对位移：因其稳态值随时间t增加而趋于无穷，可求出积分增益

K0=位移/(输入电压·t)=0.024/s

而位移对输入电压的传递函数为

1.2 广义对象的状态空间表达式

根据电动机广义对象工作机理[6]导出下述微分方程组。

转速n与位移S关系：S=k3∫wdt

式中，La为电枢电感；Ra为电枢电阻(测出实际值为8.4Ω)；Ea为电枢反电势，Ea=CeΦn；J为转动惯量；T为电磁转矩，T=CTΦn；Ce，CT为常数。

消去中间变量可得转速n对输入电压微分方程

(1)

由辨识的转速对输入电压的微分方程为

(2)

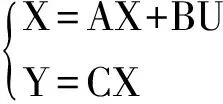
2 状态反馈阵的理论计算

2.1 系统的能控性

2.2 系统质量指标

f*(s)=(s-λ1)(s-λ2)(s-λ3)=

s3+9.414s2+12.312s+8

(3)

加有状态反馈系统的特征多项式[2]为：

1.581 5K1)s2+(36.365 3+

26.516K2)+0.872 4K3

(4)

由式(3)和式(4)对应系数相同，求出K1=-2.447 5，K2=-0.907 1，K3=9.170 1，加状态反馈后的系统结构图[5]如图1所示。

图1 设计系统状态反馈后的仿真结构图

图1中，Gain1=1.581 5，Gain2=16.766 7，Gain3=0.032 9，Gain4=-13.28，Gain5=-2.168，Gain6=-2.447 5，Gain7=-0.907 1，Gain8=

-9.170 1。

3 用Simulink计算系统性能指标

3.1 加入单位阶跃信号输入作用

3.2 系统死区非线性对系统的影响

对直流电动机而言，系统存在死区。在理论研究时我们把它当作线性系统对待，但在模拟仿真时必须考虑这个因素。经测量，该直流电动机的死区大小为±1.5V，在加载单位阶跃信号情况下， 系统加上死区特性时，得到的系统响应曲线如图3所示。

应时间变晚，产生静差，在一定程度上降低了系统超调，并且使调节时间略有变长。

图2 状态反馈理论计算参数下的响应曲线

图3 死区特性参数下的响应曲线

3.3 系统饱和特性的影响

在加载单位阶跃信号情况下，系统加饱和特性响应曲线如图4所示。

图4 饱和特性作用下系统响应曲线

由图4可看出，在加载饱和特性后系统开始响应时间较纯死区特性条件下提前了，调节时间明显变长，ts=8s。可见设计过程中，前置放大器对系统的快速响应产生了一定影响。饱和现象使系统的开环增益在饱和区时下降。控制系统在设计时，为使功放元件得到充分利用，应力求使功放先进入饱和，以此提高系统响应速度。

3.4 死区和饱和特性同时存在时对系统的影响

设计加载死区和限幅器后，系统输入单位阶跃信号，得到的响应曲线如图5所示。

图5 死区和限幅器作用下系统的响应曲线

由图5可看出，在加死区和限幅器特性的情况下，系统产生的静差ess=0.18。

3.5 状态反馈系统抗干扰特性仿真

在加载死区和限幅器后系统的仿真结构图基础上，设计有输入信号和干扰作用下的抗干扰仿真，得到系统响应曲线如图6所示。

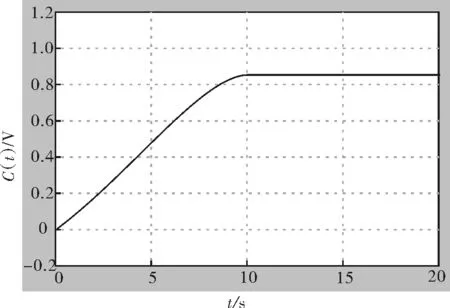
图6 在干扰作用下系统响应曲线

由图6可以看出，在加载输入信号源以及干扰信号时，系统的动态和稳态性能都没有发生变化，说明系统的抗干扰能力很强。

4 状态反馈系统的设计与实现

5 结束语

通过模拟硬件电路以及最终测试结果可知，状态反馈系统结构简单、抗干扰能力强、便于实现、参数调试简单，不像PID校正参数之间相互制约较大，为随动系统的实现找到了一个新途径。

[1]陈隆昌.控制电机[M].西安：西安电子科技大学出版社，2000.

[2]胡寿松.自动控制原理(第五版)[M].北京：科学出版社，2007.

[3]杨素行.模拟电子技术简明教程[M].北京：高等教育出版社，2006.

[4]薛定宇，陈阳泉.系统仿真技术与应用[M].北京:清华大学出版社，2004.

[5] 王孝武. 现代控制理论[M].北京：机械工业出版社，2001.

[6] 钱平. 伺服系统[M].北京: 机械工业出版社，2011.

Application of State Feedback in Designation of Servo System

SHANG Yarui, WANG Bin

(Mingde College, Northwestern Polytechnical University，Xi’an 710124, China)

This paper used state feedback to carry out the design, simulation and simulation debugging arbitrary pole of servo system. It includes servo system the identification, the establishment of the state space expression of the transfer function and state feedback coefficient matrix calculation, system simulation and debugging. State feedback system is studied with dead zone, saturation characteristics and interference characteristics of the output response curve.Through the analysis of the curve,we prove state feedback system response speed, good stability, and strong anti-jamming capability. The system parameter debugging is simple, easy to implement, circuit for the realization of the servo system has found a new way.

state feedback; servo system; Simulink simulation；simulation debugging

2015-01-20；修改日期: 2015-03-12

尚亚锐(1981-)，女，硕士，实验师，主要从事自动化方面的教学和研究工作。

G642.0

A

10.3969/j.issn.1672-4550.2015.04.005