基于模糊物元的高校实验教学质量综合评价
2015-05-08李焓
李 焓
(成都理工大学 教务处,成都 610059)
基于模糊物元的高校实验教学质量综合评价
李 焓
(成都理工大学 教务处,成都 610059)
为了减少实验教学质量综合评价过程中主观因素的影响,提高实验教学质量综合评价结果的可靠性,将物元分析理论引入到实验教学质量综合评价中,利用AHP层次分析法计算指标权重的方法,建立起模糊物元综合评价模型。并运用该模型进行了实例分析,进一步证明了该方法的可行性和有效性,为高校实验教学质量综合评价提供了新的参考和方法。
模糊物元;实验教学质量;AHP法;评价
实验教学是高校教学活动的重要组成部分,是理论联系实际的一个重要教学环节,在培养学生动手能力、分析和解决问题能力方面起着十分重要的作用[1-3]。随着教学改革的深入与发展,对高校实验教学质量的要求也越来越高,实验教学质量直接关系和影响着教学的整体质量和效果[4]。因此,对高等学校实验教学质量展开综合评价就显得十分重要。它是认识与分析实验教学效率,监控实验教学质量,推进实验教学改革的必要方法和有效手段[5]。
近年来,我国相关学者[6-10]依据实验教学的特点,通过找出与实验教学工作关系紧密的核心要素等方法,对实验教学质量评价体系的构建进行了有益的研究和探索,并构建了具有引导、调节、激励功能的评价体系,在实验教学质量评价中起到了关键性的作用。利用评价指标体系进行实验教学质量评价时,因指标体系所涉因素较多,指标体系中各单项指标间往往存在不相容性。同时,因受主观认识不确定性和模糊性的影响,指标权重的确定随意性较大。因此,选取适当的评价方法,将直接关系和影响到评价的效果和结果的准确性。
物元分析理论主要研究事物的可拓性,具有解决矛盾,化矛盾问题为相容问题的特点[11]。本文通过利用AHP法确定指标权重系数与模糊物元相结合的方法,构建起了高校实验教学质量模糊物元评价模型,并运用该模型进行了实例分析。此研究将为实验教学质量综合评价提供新的思路和方法。
1 物元熵权评价模型
1.1 物元及复合物元
物元分析法主要是用事物N、特征C和量值V,以有序三元组R=(N,C,V)作为描述事物的基本元,R简称物元[12]。如果事物N有n个特征C1,C2,…,Cn和对应的量值V1,V2,…,Vn,其物元矩阵表示为:
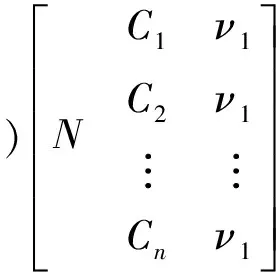
如果m个事物N1,N2,…,Nm,具有n个共同的特征C1,C2,…,Cn,事物Ni的特征Cj量值为νji,则复合物元矩阵记作:
1.2 关联函数及关联度计算
关联函数表示物元的量值为实轴上一点时, 该点符合某一水平的程度。关联函数的取值范围为整个实数轴[13]。根据可拓集合理论和具体条件,建立如下关联函数。
式中:Kj(χi)为各评价因子对应于所属评价等级的关联度;χi代表评价因子实际取得的量值;νji=
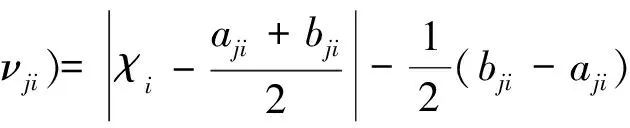

νji=(bji-aji)
1.3AHP法确定指标权重
AHP法可根据问题的性质和要求,将研究对象分解为不同组成因素,通过建立递阶层次结构、构造两两判断矩阵、层次单排序、层次总排序、一致性检验等步骤,得到评价指标的归一化权重向量,ω=(ω1,ω2,…,ωn)[14]。
1.4 综合关联度向量及评价等级
复合模糊物元与权重向量的积向量为综合关联度向量,即:
K=ω·Rmn=(κ1,κ2,…,κn) (2)
关于评价等级结果分析,对于复合模糊物元中的特征事物的行向量或者综合关联度来说,它的等级即为行向量最大值所在列的等级。
2 实例分析
为了验证模型在实验教学质量综合评价中应用的可行性和有效性,笔者选取了一门实验课作为研究对象,同时参照相关参考文献构建体系的方法[15-17],构建起了本次评价的指标体系。该评价指标体系包含了:教学计划、实验过程、实验效果3个准则层及14个评价指标项,每项指标都制定了详细的评价标准和观测值。经评价后各评价指标实际测评结果值见表1。
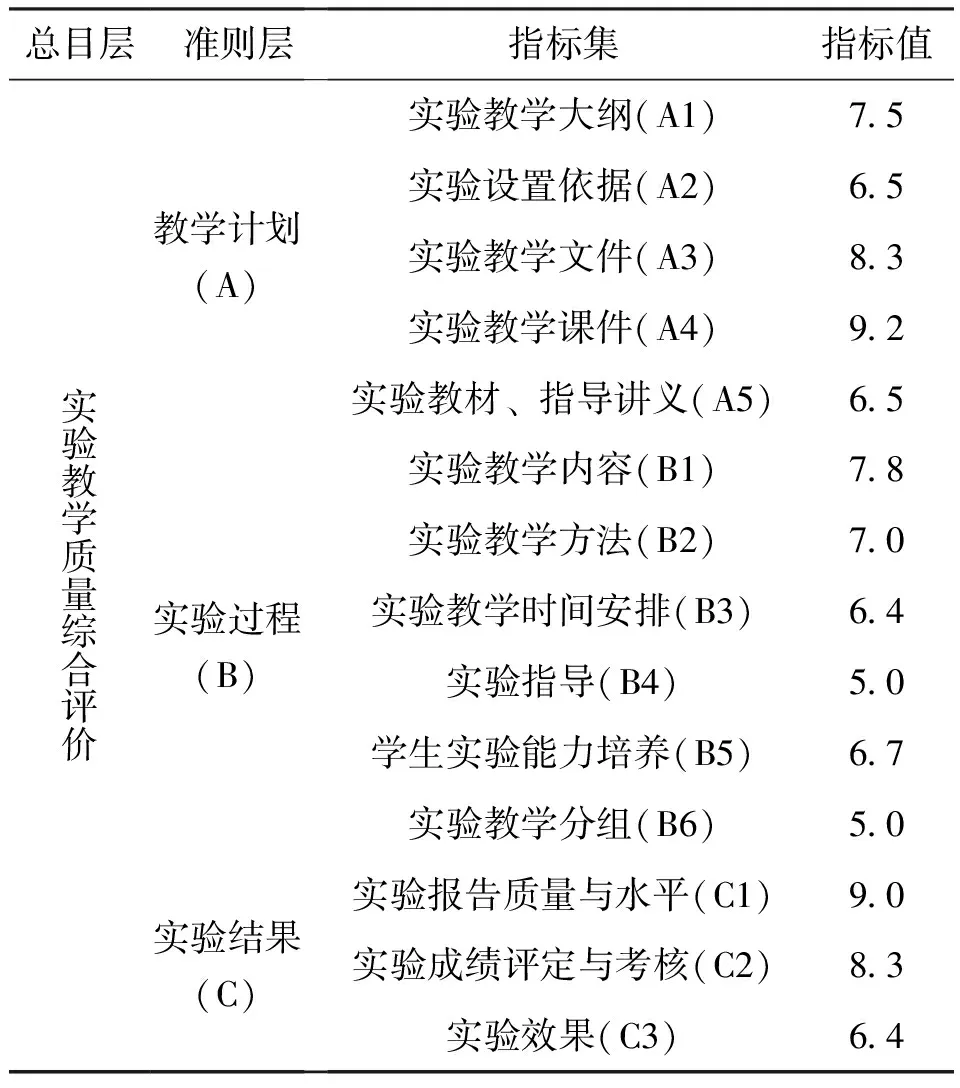
表1 实验教学质量考核指标
利用所建模型对该门实验课的实验教学质量展开综合评价分析。
2.1 模糊物元关联分析
2.1.1 评价等级划分
在评价之前,先将实验教学质量评价等级划分为Ⅰ~Ⅴ级五个评价等级,分别对应为“低”(Ⅰ级)、“较低”(Ⅱ级)、“中等” (Ⅲ级)、“较高”(Ⅳ级)、“高”(Ⅴ级),五个等级的单因素评价标准临界值分别为:(0~2)、 (2~4)、(4~6)、(6~8)、(8~10)。
2.1.2 构建复合模糊物元及关联度计算

2.2 指标权重计算
2.2.1 计算指标权重
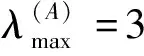
2.2.2 检验判断矩阵的一致性
判断矩阵A、B、C、D的一致性评估指标CI=(λmax-n)/(n-1),随机一致性比率CR=CI/RI,得到各判断矩阵随机一致性比率分别为:CR(A)=0.006;CR(B)=0.028;CR(C)=0.014;CR(D)=0.033;其CR值均小于0.1,故验证了判断矩阵具有满意的一致性,表明其权数分配合理。
2.2.3 综合权重
计算出二级指标相对总目标层的权重向量:
ω=(0.042,0.022,0.012,0.007,0.005, 0.102,0.040,0.044,0.023,0.021, 0.014,0.070,0.426,0.172)
ω即为实验教学质量评价指标综合权重向量。
2.3 评价结果
2.3.1 计算综合关联度
利用式(2)计算出各实验室的综合关联度向量,结果见表2。

表2 综合关联度计算结果及所属等级
2.3.2 评价结果分析
依据综合关联度最大值所对应的等级为其实验教学质量评价结果所属等级。根据表2中的综合关联度值,可知该实验教学质量评价结果所对应的等级为:“良”。
3 结束语
基于可拓理论,运用AHP层次分析法确定指标权重的方法,建立起高校实验教学质量综合评价的模糊物元综合评价模型,有效地减少评价过程中的主观性,提高了实验教学质量综合评价的客观性,从而为高校实验教学质量综合评价找到一种定量分析的新方法,为实验教学质量综合评价研究提供了新的参考。
[1]卫绍元,王彤,卢曼慧. 优化实验教学质量监控体系,提高实验教学质量[J].实验技术与管理,2009,26(3):225-226.
[2] 秦昌明,时祖光. 高校实验教学质量评价体系的构建与实践[J].黑龙江教育,2010(5):22-23.
[3]王晓红. 实验教学质量监控系统的探讨[J].江苏大学学报,2002,24(1):47-50
[4] 王红萍,刘青广,赵亚红.高校实验教学质量监控体系的构建[J].中国成人教育,2008(12):123-124.
[5] 高海洲,刘金华.实验教学环节质量标准与评价方案的研究[J] .中国教育技术装备,2007(12):10-12.
[6] 杨琴.创新理念下的高校实验教学质量保障改革[J].实验科学与技术,2011,9(1):101-104.
[7]陈阿梅,秦军伟,呼汉卫.实验教学质量监控体系的研究与探索[J].实验技术与管理,2011,28(7):251-253.
[8]周合兵,祝凤荣,陈琦.构建实验教学质量保障体系的实践与探索[J].实验室研究与探索,2006,25(6):713-716.
[9]叶辉, 程备久, 胡文友, 等.高等院校实验教学质量监控体系的构建与实施[J].高等农业教育, 2005(10): 40-42.
[10]刘宏达,马忠丽. 高校实验课程教学质量评价体系的构建[J] . 中国现代教育装备,2009(3):60-63.
[11]蔡文.物元模型及其应用[M].北京:科学技术文献出版社,1994.
[12]李焓.模糊物元模型在实验室绩效评价中的应用[J].实验科学与技术,2014,12(1):176-179.
[13]高宏.基于核心能力的战略进化与管理评估的物元模型[J].系统工程,2011(5):55-61.
[14]李伯年.模糊数学及其应用[M].合肥:合肥工业大学出版社,2007.
[15]刘嘉南,胡今鸿,王晓迪.高校实验教学质量保障与评价体系探析与实践[J].实验技术与管理,2013,30(8):129-131.
[16]贾晓东.高校实验教学质量的模糊综合评价[J].山东理工大学学报:自然科学版,2007,21(5):77-80.
[17]陈凤姣,徐正华.模糊评判法在高校实验教学质量评价体系的应用[J].漳州师范学院学报:自然科学版,2010(4):152-155.
Comprehensive Evaluation of Experiment Teaching Quality in University Based on Fuzzy Matter-element
LI Han
(Office of Teaching Affairs, Chengdu University of Technology, Chengdu 610059, China)
In order to reduce the subjective influence on the comprehensive evaluation of the quality of experimental teaching process, improve the reliability of the comprehensive evaluation of the results of the experiment teaching quality, this model of comprehensive evaluation of experiment teaching quality is established. By introducing matter element analysis theory and applying the AHP analysis method to calculate the weight of every index, the model is used to analyze an example, which further proves the feasibility and effectiveness of the method. This provides new reference methods for the research of comprehensive evaluation of experiment teaching quality in college.
fuzzy matter-element; experiment teaching quality; AHP method; evaluation
2014-07-07;修改日期: 2014-11-20
成都理工大学教学改革基金资助项目(13JG Y91)。
李 焓(1978—),男,硕士,助理研究员,研究方向:教学与管理。
G642.423
A
10.3969/j.issn.1672-4550.2015.03.039
