腐蚀损伤下海洋平台动力响应研究

薛洪志， 嵇春艳

(江苏科技大学， 江苏 镇江212003)

腐蚀损伤下海洋平台动力响应研究

薛洪志， 嵇春艳

(江苏科技大学， 江苏 镇江212003)

基于线性莫里森方程和随机波浪理论，建立了随机波浪载荷计算方法，以此分析极端海况下极值波浪力的统计特性。以墨西哥湾某海域一导管架海洋平台为算例，建立有限元腐蚀模型，分别计算平台在极值随机波浪载荷作用下的动力响应。将无腐蚀和腐蚀两种状态下的动力响应对比分析，计算结果显示，腐蚀损伤对动力响应的影响较明显，相同载荷作用下动力响应随腐蚀厚度呈线性变化。

动力响应；极值波浪载荷；腐蚀损伤；导管架平台

0 引言

导管架平台是一种近海石油勘探和开采应用范围较广的平台类型。海洋平台常年服役在恶劣的海洋环境中，时常受到风、波浪、流等载荷交互作用，其中平台所承受的环境载荷主要为波浪载荷。随着平台工作水深的增加，平台结构必然增大，反而使平台抗弯刚度下降，在极值波浪载荷作用下平台结构运动响应幅度加大，严重影响到平台疲劳强度和极限强度，威胁平台工作的安全性与可靠性。

现有的波浪载荷计算方法主要有莫里森方程和绕射理论。由于导管架平台构件的直径与波长比小于0.2，故计算导管架平台所承受的波浪载荷采用莫里森方程。张学志等[1]采用非线性莫里森方程，考虑流固耦合作用建立海洋平台动力时程分析方法，计算结果表明，在极端海况下，该分析方法更符合实际情况。居艮国等[2]分析了钢管平台在随机波浪力作用下的动力响应，以及附加水质量和动力阻尼对结构随机动力响应的影响。付方等[3]应用ANSYS软件对导管架平台进行动力分析，并考虑随机波浪作用，对平台结构进行可靠性分析。Elshafey等[4]研究导管架试验模型在随机波浪力作用下的动力响应，与计算结果吻合较好。何晓宇等[5]研究导管架海洋平台在地震与波浪联合作用下的动力响应特性，分析结果显示，抗震设防烈度较低及较大风浪条件下，对平台结构进行抗震分析时要考虑地震与波浪的联合作用。海洋平台服役在恶劣的海洋环境中，腐蚀损伤和裂纹损伤是极为常见的结构缺陷，对具有不同损伤的海洋平台的动力响应分析显得尤为重要。

1 腐蚀损伤下海洋平台动力分析方法

1.1 腐蚀数学模型

腐蚀作用的影响通常表示为材料厚度的折减，并且腐蚀过程极为复杂，但现有的腐蚀模型大多都是在均匀假设的基础上提出的，多采用线性腐蚀模型[6]：

式中：r(t)为材料腐蚀厚度；ri为年腐蚀速度；t0为腐蚀保护系统寿命。

不考虑腐蚀保护系统的作用，即海洋平台服役后腐蚀开始发生，假定暴露在海水中的海洋平台构件以每年0.15mm的速度发生腐蚀，暴露在大气中的平台构件以每年0.05mm的速度发生腐蚀[7]。

1.2 腐蚀损伤下海洋平台运动方程

腐蚀作用使得材料厚度降低，同时平台质量矩阵和刚度矩阵也下降。采用有限元方法将腐蚀损伤下的海洋平台离散为几个自由度的有限元系统，则海洋平台的运动方程表示为：

1.3 随机波浪载荷计算方法

采用莫里森方程[8]来计算随机波浪载荷，方程如下：

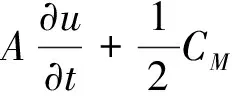
采用谱分析法来计算桩柱上的波浪力谱，经傅里叶变换为时域下的波浪力，波浪力谱表示为：

[TFη(ω)

式中：Sη(ω)为不规则波的谱；SFη(ω)为波浪力F的谱；TFη(ω)为波面到波浪力的传递函数；N(z)为形函数；σu为水质点水平速度u的均方根差；d为水深；k为波数。

2 极端海况下极值波浪载荷预报

为了得到极端海况下的波浪载荷，首先对极值波浪载荷波高进行预报，该文采用Gumbel概率分布来预报极值波浪载荷波高，其形式为：

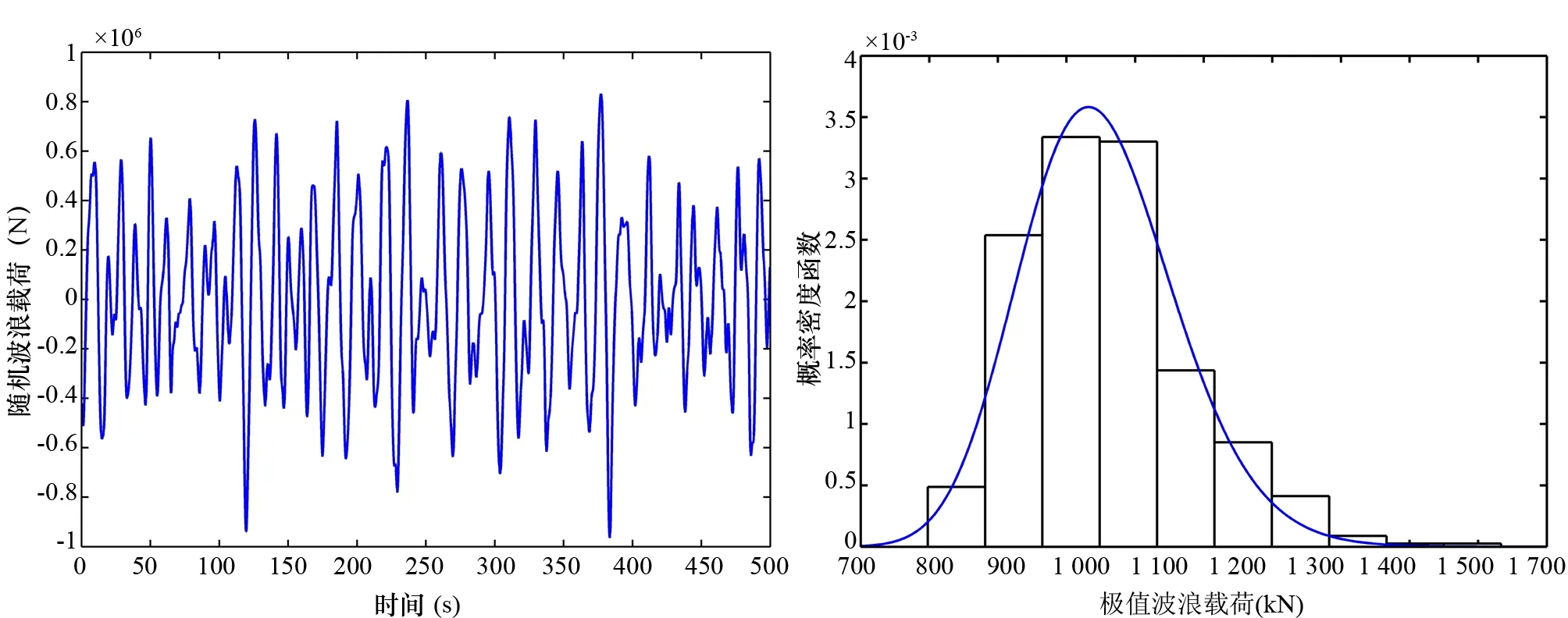
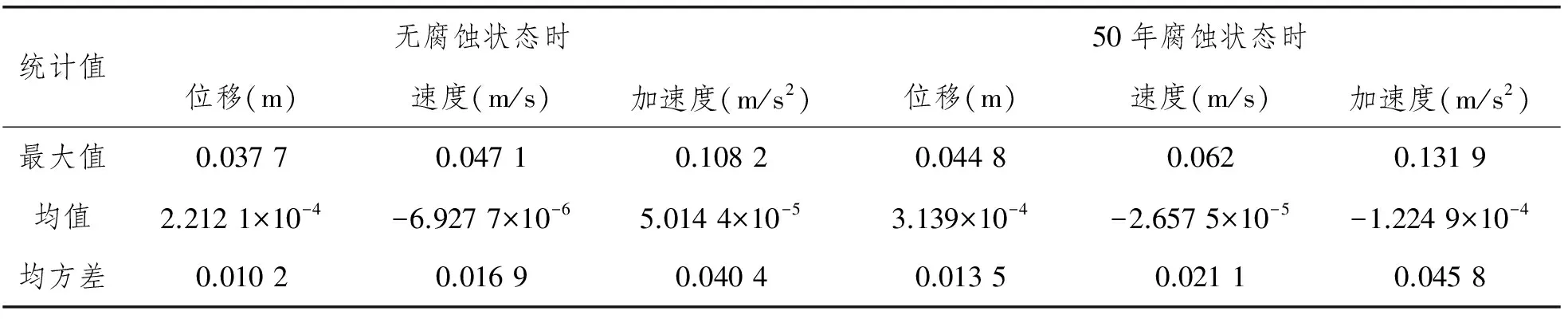
Pr(SWH

式中：Pr(SWH

文中a和b分别取0.743和5.125，最大波高SWH取11.32m[9]，通过波高概率分布函数，计算得到各重现期内的极值波高，见表1。

表1 重现期内极值波高

3 算例

3.1 海洋平台概况

以墨西哥湾某海域一典型八桩腿式导管架海洋平台为例，该平台由桩腿、导管、横撑及斜撑组成，平台高度为119 m，平均工作水深为105 m，导管直径随水深由1.6 m～2.4 m变化，导管厚度由40 mm～45 mm变化，海洋平台主要尺寸见表2。

表2 海洋平台主要尺寸

3.2 极值波浪载荷统计值

选取JONSWAP谱，基于MATLAB程序编写随机波浪载荷计算程序，通过计算得到作用在单个桩体上的随机波浪载荷的时域结果，如图1所示。应用该计算程序逐次计算1 000次，将得到的极值波浪力进行统计分析，极值波浪力近似符合正态分布，如图2所示，极值波浪力统计值见表3，由表3可知，平台服役年限越长所遭遇的风险越大，降低了平台作业时的安全可靠性。

图1 平台50重现期内随机波浪载荷 图2 平台50重现期内极值波浪载荷概率分布

3.3 海洋平台动力响应分析

基于ANSYS软件，桩腿、导管和横斜撑分别采用PIPE59单元和PIPE16单元建立，采用MASS21质量单元模拟甲板上的机械设备重量，底部采用固端约束，如图3所示。将随机波浪载荷施加到水平面处X轴方向节点上进行瞬态分析，得到平台响应测点在随机波浪载荷作用下的位移、速度及加速度值。

3.3.1 无损伤状态下海洋平台动力响应分析

不考虑腐蚀损伤对平台的影响，将不同重现期内的波浪载荷导入ANSYS软件中进行响应计算，文中仅给出平台在5年重现期和50年重现期内的响应对比分析，图4～图6分别给出测点X轴方向的位移、速度及加速度的对比曲线，表4给出测点X轴方向响应的最大值、均值和均方差。由图4～图6可知，5年重现期内动力响应均小于50年重现期内的动力响应。由表4可知，在随机波浪载荷作用下海洋平台的动力响应较为明显，50年重现期内与5年重现期内相比，平台测点X轴向最大位移增加90.4%，最大速度增加53.92%，最大加速度增加40.34%，表明随机波浪载荷越大对平台动力响应的影响越大，尤其是对位移的影响更为明显。

统计值5年重现期50年重现期位移(m)速度(m/s)加速度(m/s2)位移(m)速度(m/s)加速度(m/s2)最大值0．01970．03060．07710．03770．04710．1082均值-6．9701×10-54．5461×10-5-3．8378×10-62．2121×10-4-6．9277×10-65．0144×10-5均方差0．00670．01110．02650．01020．01690．0404

3.3.2 损伤状态下海洋平台动力响应分析

计及材料腐蚀损伤，将50年重现期内的随机波浪载荷作为环境载荷对腐蚀平台模型进行动力计算，文中仅给出无腐蚀和腐蚀两种状态下的动力响应对比，图7～图9给出X轴向测点位移、速度及加速度的对比曲线，表5给出测点X轴方向运动响应的统计值。由图7～图9可知，腐蚀损伤下海洋平台动力响应较无腐蚀损伤时动力响应大，平台测点X轴向最大位移增加18.83%，最大速度增加31.63%，最大加速度增加21.9%，腐蚀损伤对平台运动响应影响较大，对速度的影响更为明显。图10给出腐蚀平台在相同波浪载荷作用下最大位移随腐蚀厚度的变化曲线，由图10可知，极值位移随腐蚀厚度呈线性变化，腐蚀越严重位移响应越大。

图7 无腐蚀和腐蚀状态时测点X轴向位移对比 图8 无腐蚀和腐蚀状态时测点X轴向速度对比

图9 无腐蚀和腐蚀状态时测点X轴向加速度对比 图10 测点X轴向极值位移随腐蚀厚度变化曲线

表5 平台测点X轴方向运动响应

4 结论

基于莫里森方程和随机波浪理论，建立随机波浪载荷计算方法，并通过对极端海况进行预报，获得不同重现期内的最大波高。以墨西哥湾某海域一导管架平台为算例，采用随机波浪载荷计算方法，分别对不同重现期内的海洋平台动力响应进行计算，计算结果表明：随机波浪载荷越大，平台动力响应越明显，尤其位移响应较速度和加速度响应更明显；腐蚀损伤下海洋平台的质量和刚度均下降，腐蚀损伤对平台动力响应影响较为明显，其中对速度的影响较大；在相同波浪载荷作用下平台极值响应随腐蚀厚度呈线性增加。

[1] 张学志，黄维平，李华军．考虑流固耦合时的海洋平台结构非线性动力分析[J]. 中国海洋大学学报，2005，35(5)：823-826．

[2] 居艮国，吕风梧，王彬．波浪力作用下钢管桩施工平台随机动力响应分析[J]. 铁道科学与工程学报，2006，3(5)：70-74．

[3] 付方，陆建辉，李玉辉.随机波浪载荷下CII海洋平台结构可靠性分析[J]. 石油工程建设，2006,32(6):22-26.

[4] Ahmed A E, Mahmoud R H, Marzouk H. Dynamic response of offshore jacket structures under random loads [J]. Marine Structures, 2009, 22:504-521.

[5] 何晓宇, 李宏男. 地震与波浪联合作用下海洋平台动力特性分析[J]. 海洋工程,2007, 25(3):18-25.

[6] Paik J M, Anil K T et al. A time-dependent corrosion wastage model for seawater ballast tank structures of ships [J]. Corrosion Science, 2004, 46:471-486.

[7] Melchers R E. Corrosion uncertainty modeling for steel structures [J]. Journal of Constructional Steel Research. 1999，52:3-19.

[8] 俞聿修. 随机波浪及其工程应用[M]. 大连：大连理工大学出版社，2000.

[9] Panchang V G，Li D C. Large waves in the Gulf of Mexico caused by hurricane Ivan [J]. Bulletin of the American Meteorological Society, 2006, 87(4):481-489.

Dynamic Response Study of Jacket Platforms with Corrosion under Random Wave Loads

XUE Hong-zhi，JI Chun-yan

(Jiangsu University of Science and Technology, Jiangsu Zhenjiang 212003, China)

Based on linearized Morison equation and random wave theory, the calculation method of stochastic wave load was proposed in order to analyze the statistical properties of extreme load under extreme sea condition. Taking a typical Jacket platform as the example, the FE model with corrosion for calculating dynamic response of platform under extreme wave loads was studied well. Comparing of dynamic response with corrosion and uncorrosion showed that the dynamic response of Jacket platform varied linearly with the thickness of corrosion.

dynamic response; extreme wave load; corrosion damage; jacket platforms

2014-01-21

国家自然科学基金项目(51079065)；江苏省普通高校研究生科研创新计划项目(CXZZ13_0724)。

薛洪志(1985-)，男，硕士研究生。

1001-4500(2015)02-0085-06

P75

A