自适应交互多模型的PHD粒子滤波多机动目标跟踪*

危 璋,冯新喜,毛少锋

(空军工程大学信息与导航学院, 西安 710077)

自适应交互多模型的PHD粒子滤波多机动目标跟踪*

危 璋,冯新喜,毛少锋

(空军工程大学信息与导航学院, 西安 710077)

针对多机动目标跟踪中采用统一固定模型转移概率的问题,提出一种在线估计模型转移概率的自适应多模型PHD滤波(AIMM-PHD)。首先保留模型的采样粒子及其似然度;其次根据粒子的分类结果,计算出每个目标对应每个模型的状态输出;最后将输出交替作为模型输入进行滤波,计算出目标的模型转移概率。实验表明:相较于IMM-PHD,所提AIMM-PHD有较低的OSPA误差,目标个数估计更准确,且时间只增加了8.1%,从而证明了该算法的有效性。

概率假设密度;交互多模型;自适应模型转移概率

0 引言

在多目标跟踪领域,传统的基于数据关联的处理方法由于存在组合爆炸等问题,计算量很大。R.Mahler在2000年将随机集理论运用于多目标跟踪领域[1],在贝叶斯滤波的框架下,引入概率假设密度(PHD)的概念,实现了免关联的多目标跟踪,并将多目标跟踪中的起始、维持以及消亡统一到一个算法流程。目前PHD主要的实现方式有序贯蒙特卡洛PHD(SMC-PHD)[2]和混合高斯PHD(GM-PHD)[3]。

目标跟踪的精度在很大程度上取决于运动模型与目标实际运动模式的匹配程度,由于单一的运动模型很难准确描述目标的运动模式,基于多模型方法的机动目标跟踪因在跟踪性能和计算量上获得较好的

平衡而被广泛应用[4]。文献[5]将多模型算法与PHD粒子滤波进行了结合,但是存在模型退化的问题。文献[6-7]则是实现了多模型的GM-PHD滤波。文献[8]则是在保持每个模型粒子个数不变的条件下实现了粒子的交互过程。

目前基于交互多模PHD滤波的多机动目标跟踪大多采用一个固定不变的模型转移概率矩阵,而在很多情况中(如跟踪非合作目标),一个运动目标模型转移概率矩阵是未知且时变的,并且每个目标的模型转移概率矩阵一般是不同的。文中基于上述考虑,提出一种自适应在线估计模型转移概率矩阵的PHD粒子滤波算法。在每次估计出目标个数以及状态之后,根据贝叶斯公式,将最新量测信息考虑在内,在线估计每个目标的基于后验概率的模型转移概率矩阵。

1 PHD滤波原理及PHD粒子(SMC-PHD)滤波流程

1.1 PHD滤波原理

PHD滤波包括预测和更新两个步骤:

ek|k-1(xk-1)fk|k-1(xk|xk-1)]·

Dk-1|k-1(xk-1|Z1:k-1)dxk-1

(1)

Dk|k(xk|Z1:k)=(1-PD(xk))Dk|k-1(xk|Z1:k-1)+

(2)

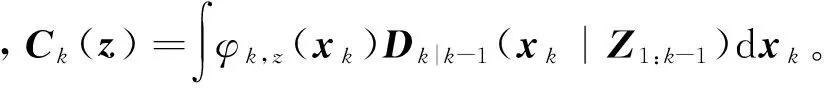
1.2 SMC-PHD算法流程

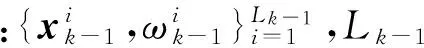
PHD预测:

(3)

(4)

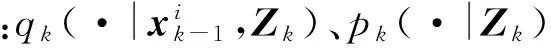
PHD权值更新:

(5)

重采样:

对所有粒子权重求和得到目标个数:

(6)

粒子集进行正规化:

(7)

对正规化的粒子集进行重采样得到归一化的粒子集:

(8)

将式(8)中得到的粒子集中的每个权值乘上Nk|k就得到k时刻重采样后的PHD。

目标个数和状态估计:

PHD在状态空间上的积分为目标个数,因此由式(6)得到的即为目标个数,对于状态的提取有很多种方法,典型的算法可以参阅文献[9-10]。

2 自适应多模型的PHD粒子滤波

2.1 交互多模型PHD粒子滤波[8]

假设在k时刻第m(m=1,2,…,M)个模型的方程为:

(9)

(10)

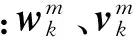
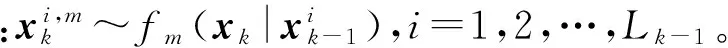
定义每个粒子i对每个模型的似然度为[8]:

(11)

其中:nzk表示量测个数。

模型概率为:

(12)

(13)

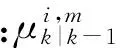
由抽样粒子以及模型概率可以得到多模型的混合粒子:

(14)

对于新生目标粒子的计算,在完成采样后,可以设定各粒子模型的概率为同一值:1/M。

到此完成了对各粒子状态的交互和各粒子对每个模型概率的计算,接下来需要计算各粒子的权值。

计算每个混合粒子的预测权值:

(15)

2.2 模型转移概率自适应算法

由于在实际中,模型转移概率矩阵是难以准确知道的,而且对于多机动目标而言,模型转移概率矩阵一般是不相同的,因此有必要在线估计各目标对应的模型转移概率。

k时刻模型转移概率为:

其中:mj(k)表示k时刻模型为j;Zk-1表示从开始到k-1时刻的量测集合;zk表示k时刻的量测。

p{zk|mj(k),mi(k-1),Zk-1}=

N(zk:zk|k-1Sij(k))

(17)

表示以k-1时刻模型i的状态估计作为k时刻模型j的输入时所求的似然函数,Sij(k)表示新息协方差阵。

(18)

(19)

Sij(k)=E{vij(k)(vij(k))′}

(20)

由于Zk-1中不包含k时刻的量测信息,因此有:

p{mj(k)|mi(k-1),Zk-1}=πij(k-1)

(21)

p{zk|mi(k-1),Zk}=

p{mj(k)|mi(k-1),Zk-1}

(22)

2.3 基于PHD粒子滤波的模型转移概率矩阵自适应算法

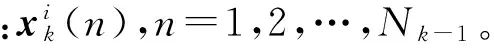
(23)

方差为:

(24)

若式(9)与式(10)中fm与hm均为非线性方程,则式(16)中涉及的预测量测以及似然函数的计算可通过类似EKF、UKF、QKF或CKF的方法得到。下面以CKF为例进行推导。

时间预测:

1)计算容积点

l=1,2,…,2nx

2)传播容积点

3)预测均值及预测协方差

(25)

(26)

量测预测:

1)计算容积点

2)传播容积点

(27)

3)新息协方差计算

其中:i表示第i个量测。

根据式(17)计算每个量测的似然度:

p{zk(i)|mj(k),mi(k-1),Zk-1}=

(29)

第n个目标的第m个模型的似然度取最大似然值:

p{zk|mj(k),mi(k-1),Zk-1}=

(30)

由式(29)、式(21)和式(22)得出每个目标的模型转移概率矩阵。

3 实验仿真

3.1 实验场景设定

假设初始时刻存在两个目标,初始状态分别为:[100 100 1 000 -100]′和[100 100 -1 000 100],第三个目标出现时刻为第20s,初始状态为:[150 100 3 000 0]。每个周期内的杂波个数为10,在观测区域服从均匀分布。目标存活概率为1,检验概率为0.95。观测站位于(0,0),直角坐标系下观测区域为[-2 000 3 500]×[-4 0004 000]。目标跟踪模型如下:

X(k)=FX(k-1)+w(k)

(31)

(32)

其中:X(k)=[x(k)vx(k)y(k)vy(k)]′,(xst,yst)表示观测站位置。模型集由一个匀速模型和两个转弯模型组成。

(33)

(34)

3.2 实验结果及分析

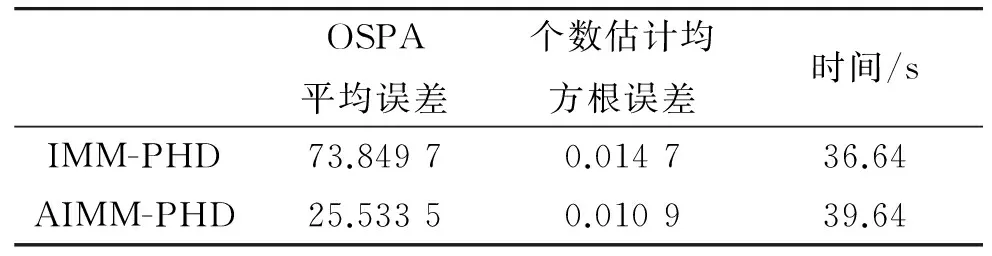
表1 性能对比表

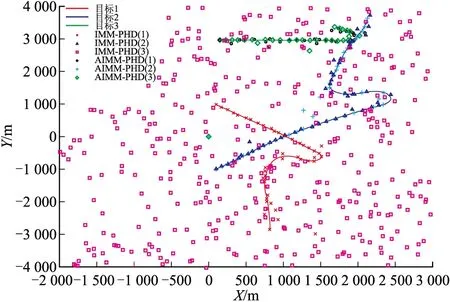
图1 目标轨迹图

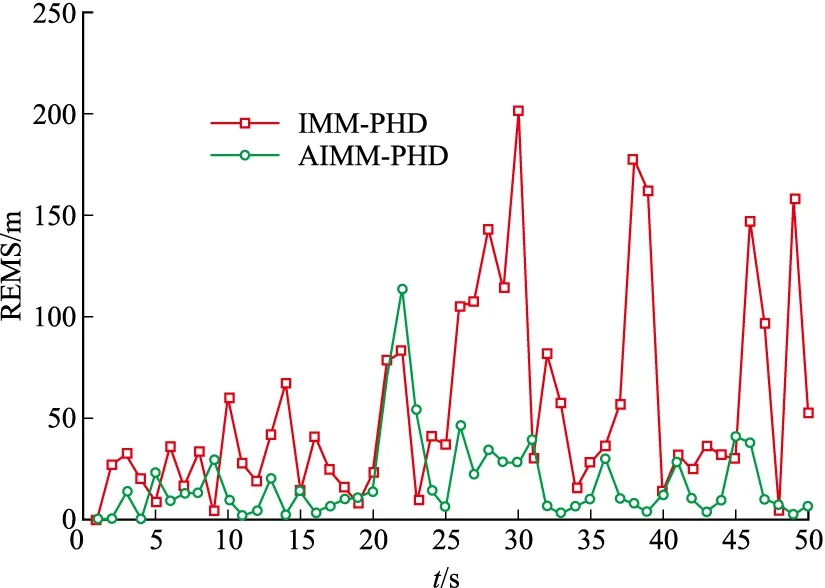
图2 OSPA距离图

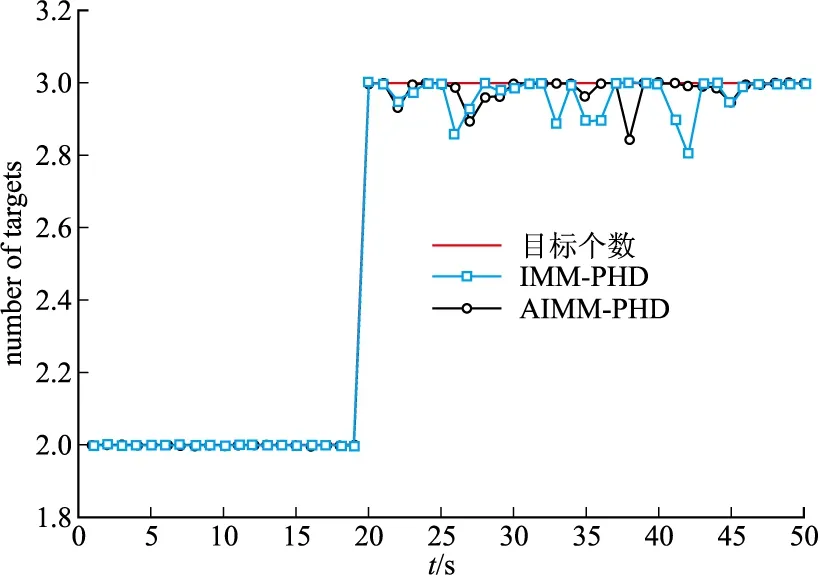
图3 目标个数估计图

从图1中知道交互多模型PHD(IMM-PHD)粒子滤波和自适应交互多模型PHD(AIMM-PHD)粒子滤波都能较好的跟踪多机动目标。从图2和表1知道AIMM-PHD跟踪多机动目标OSPA距离小于IMM-PHD,当目标未发生机动时,两种算法的OSPAP误差都比较小且相差较小。当目标发生机动时,IMM-PHD的误差急剧增加,而且误差变小的过程较为缓慢,而在机动时刻AIMM-PHD误差显著小于IMM-PHD,这是由于IMM-PHD在整个滤波过程3个目标用的是固定不变的模型转移概率矩阵,而AIMM-PHD采用的是在线估计出来的模型转移概率矩阵,而且估计出每个目标的模型转移概率矩阵,这样能实时地反映出每个目标的机动模式并调整模型概率。图3是目标个数估计图,在目标未发生机动时,两种算法都能很好的估计出目标个数,当目标发生机动时,两种算法对目标个数的估计都出现较大误差,AIMM-PHD滤波目标个数估计均方根误差略小于IMM-PHD滤波(表1)。从表1中知道,AIMM-PHD的滤波时间多于IMM-PHD,这是由在线估计模型概率转移矩阵造成的,但仅增加了8.1%。

4 结论

PHD滤波可以较好的跟踪个数变化的多目标,但在目标发生机动时,需要处理目标运动模式的不确定性。基于多模型的PHD滤波可以较好的解决此问题,但在实际中模型转移概率矩阵是未知的,并且每个目标的模型转移概率是不同的,基于此,文中提出一种在线估计各目标模型转移概率矩阵的算法,实验表明该算法有较低的误差,较高的目标个数估计精度,同时时间增加量不大。

[1] R Mahler. Multitarget Bayes filtering via first-order multitarget moments [J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.

[2] Ba-Ngu Vo, Sumeetpal Singh, Arnaud Doucet. Sequential Monte Carlo methods for multi-target filtering with random finite sets [J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224-1245.

[3] Ba-Ngu Vo, Wing-Kin Ma. A closed-form solution for the probability hypothesis density filter [C]∥ 2005 7th International Conference on Information Fusion, Philadelphia, PA, USA, 2005: 856-863.

[4] 周政, 刘进忙, 李振兴. 基于STC-IMM结构的自适应多模型跟踪算法 [J]. 控制与决策, 2013, 28(8): 1226-1230.

[5] K Punithakumar, T Kirubarajan, A Sinha. Multiple-model probability hypothesis density filter for tracking maneuvering targets [J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 87-98.

[6] Ba-Ngu Vo, Ahmed Pasha, Hoang Duong Tuan. A Gaussian mixture PHD filter for nonlinear jump Markov models [C]∥ Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, December, 2006: 3162-3167.

[7] Wood, Trevor M. Interacting methods for manoeuvre handling in the GM-PHD filter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 3021-3025.

[8] 王晓, 韩崇昭. 用于机动目标跟踪的多模型概率假设密度滤波器 [J]. 西安交通大学学报, 2011, 45(12): 1-5.

[9] Tobias M, Lanterman A D. Probability Hypothesis density-based multitarget tracking with bistatic range and doppler observations [J]. IET, Radar, Sonar and Navigation, 2005, 152(3): 195-205.

[10] Daniel E Clark, Judith Bell. Multi-target state estimation and track continuity for the particle PHD filter [J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4): 1441-1453.

[11] 罗笑冰, 王宏强, 黎湘. 模型转移概率自适应的交互式多模型跟踪算法 [J]. 电子与信息学报, 2005, 27(10): 1539-1541.

[12] Cheng Ouyang, Hong-bing Ji, Zhi-qiang Guo. Extensions of the SMC-PHD #lters for jump Markov systems [J]. Signal Processing, 2012, 92(6): 1422-1430.

[13] 鉴福升, 徐跃民, 阴泽杰. 改进的多模型粒子滤波机动目标跟踪算法 [J]. 控制理论与应用, 2010, 27(8): 1012-1016.

PHD Particle Filter Method for Tracking Maneuvering TargetsBased on Adaptive Interactive Multiple Models

WEI Zhang,FENG Xinxi,MAO Shaofeng

(Information and Navigation College, Air Force Engineering University, Xi’an 710077, China)

To solve the problem that multiple model probability hypothesis density (IMM-PHD) filter for maneuvering target tracking uses the prior model transition probability, a adaptive algorithm to Markova transition probability proposed. Firstly, the particles and the likelihood every model in the process of particles interaction, and then the output of every model to every target according to assortment in the process of state estimation, lastly, the model transtions probability by Bayes principle. The results show:compared IMM-PHD, AIMM-PHD has lower OSPA error; higher accuracy of target number estimation but its time only increases 8.1%, thus the effectiveness of the proposed algorithm.

probability hypothesis density; IMM; adaptive model transition probability

2014-05-03

危璋(1989-),男,湖南湘阴人,硕士研究生,研究方向:目标跟踪。

TN953

A