弹载地磁传感器时变误差的校正*

黄 坤,田晓丽,王瑞华,白敦卓,马迎辉,冯冰玉

(1 中北大学机电工程学院, 太原 030051; 2 晋西工业集团有限责任公司, 太原 030027;

3 豫西工业集团有限公司, 河南南阳 473000; 4 中国兵器工业第208研究所, 北京 102202)

弹载地磁传感器时变误差的校正*

黄 坤1,田晓丽1,王瑞华2,白敦卓3,马迎辉4,冯冰玉2

(1 中北大学机电工程学院, 太原 030051; 2 晋西工业集团有限责任公司, 太原 030027;

3 豫西工业集团有限公司, 河南南阳 473000; 4 中国兵器工业第208研究所, 北京 102202)

在弹箭设计过程中,为了获得弹体飞行时的气动参数,通常采用地磁传感器来测量弹体的姿态信息,而采用的三轴磁传感器都存在误差,因此,对误差的校正就显得很有必要了。在文中提出了一种新的校正方法,该方法是对已有的常规误差校正方法的扩展,使之能用来对磁传感器的时变误差进行校正。这种方法可用于复杂电磁环境中的弹载测量系统,可以有效校正磁传感器的测量误差,最后通过仿真实验数据对结果进行了验证。

弹箭;地磁;时变误差;校正

0 引言

在靶场射击实验所用的测量系统中,对于测量姿态的地磁测量模块,其周围还有一系列配套硬件,比如控制器模块、电源模块、数传系统等。因为所处环境复杂,这些电子器件的电流会发生变化,而变化的电流会产生相应的随时间变化的磁场,从而影响地磁测量模块测量精度,最终会导致无法保证整个系统测量的准确性与稳定性。所以文中提出一种可用于地磁时变误差校正的方法,用来降低由变化电流引起的随时间变化的磁场的影响。

1 地磁误差简介

通常情况下,使用磁传感器测量弹体姿态信息时,受到的误差有两种——常量误差和时变误差。其中常量误差主要包括:软铁误差、硬铁误差、标度系数误差、零点漂移和非正交误差。软铁误差是使用软铁材料本身引起的;硬铁误差是由地磁组件周围不确定的磁场导致的;标度系数误差是由测量轴的灵敏度的差异导致的;零点漂移是磁传感器在使用过程中,内部剩磁以及电路漂移等所导致的输出漂移;非正交误差则是由制造工艺的局限性引起,导致测量轴不能和完美正交配置完全重合;时变误差主要是由载流导线变化的电流引起的,变化的电流产生的磁场导致地磁测量产生误差。对于校正各种常量误差,一般有很多种算法可以使用,比如:两步估计法。第一步提供初始校正系数,该系数通过定心估计得到;第二步改进参数,采用高斯-牛顿法迭代处理参数。几何法,用椭圆参数补偿来估计。现有的能预防时变误差的方法

也有很多种,比如在物理上隔绝,采用屏蔽罩将地磁组件与会产生磁场的元器件隔开,从而降低其他磁场的影响。文中提出一种新的方法,通过扩展现存的常量误差校正方法,使之对磁传感器的时变误差校正也有效。

2 误差校正方法

2.1 常量误差分析

在描述新方法之前,先对已经存在的常量误差估计法进行描述。通常,传感器的校正需要两步:1)建立传感器模型;2)估计模型参数。磁传感器常量误差的模型如下所示:

(1)

(2)

Bzcosφcosλ+z0+ηz

(3)

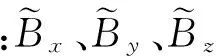
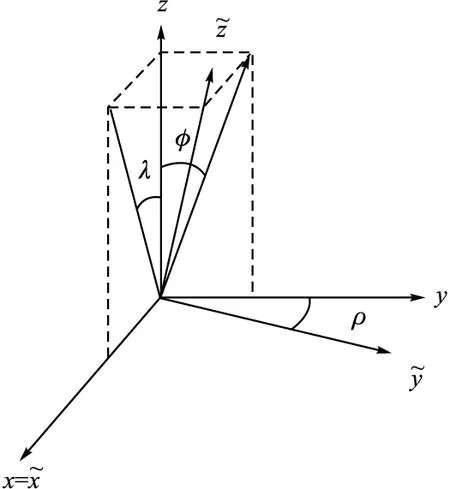
图1 几何模型

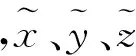
其实,此处校正的真正目的就是估计a、b、c、x0、y0、z0、ρ、λ和φ这几个参数。在上述地磁模型中有两个假定:1)地磁组件和误差源依附于同一个载体;2)软铁材料是线性的(没有磁滞现象),那么相应的它使用的标度系数a、b、c就是线性的。通过上述磁传感器模型虽然能够获取总的误差,但是不可能通过上述方法获取到每一个独立的误差。比如:磁传感器的每一个轴x0、y0、z0的误差都会受到硬铁误差和零点漂移的影响。相似的,软铁和传感器的内在比例都会对地磁的标度系数a、b、c产生影响。还有软铁误差和物理的非正交误差都可以表现在ρ、λ、φ三个角度上。虽然不能够清晰的观测到每一种误差源,但是通过对总的误差、线性比例、非正交参数的估计就已经足够校正地磁的测量值了。因为校正参数本身与弹体的姿态无关,而仅仅与磁场大小有关,所以已知磁场BE的大小就可以辨识出校正参数。由于辨识过程中涉及到的最小化问题,所以式(1)～式(3)可以被改写为关于地磁场分量作为测量值和校正参数的函数。磁场测量值的平方由下式给出:

(4)

2.2 时变误差分析

由于地磁的时变误差是由于周围载流导线电流的变化引起的,因此校正时变误差关键就是获取周围电子器件的电流变化量。文中假定导线的几何形状、地磁的位置和方向相对于导线是恒定的,那么在磁传感器周围产生的磁场就可以被写为一个线性的与电流相关的函数。这将产生以下地磁模型:

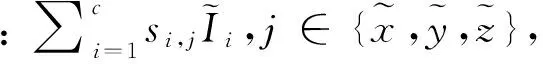
有了电流的测量值、地磁的测量值和预期磁场的大小,然后再通过上述方法就可以完成磁传感器时变误差的校正。在式(5)～式(7)的地磁模型中,有(9+3c)个校正参数,它们的估计方法与上面描述的方法相同,也是测量值与预期磁场值的最小偏差。通过梯度优化方法来实现最小化,使用牛顿迭代法反复求解直到损失函数J达到最小为止,此时即为得到最优解。其式如下:

(8)

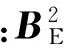
损失函数J是一个四次方的函数,它可能导致结果收敛到不正确的最小值。对于上述校正算法可以采用定心法来把损失函数从四次方降低到两次方,从而满足系统的需要。

3 实验分析

根据上述模型,在Matlab中编写程序,图2为某弹载磁传感器在某个已知的磁场中接收到的数据即测试值,根据样本数据,使用最小方差原理对模型进行辨识,以待校正的参数为输入参数,将损失函数J设为目标函数。得到校正参数为零偏误差x0=0.43 μT,y0=0.59 μT,z0=0.1 μT;标度系数误差a=0.89,b=0.9,c=1.13;非正交误差ρ=0.000 1,λ=0.000 5,φ=0.000 7;Sij=0.02 μT/mA;I=5 mA。辨识结果如图3所示。

图2 测试值

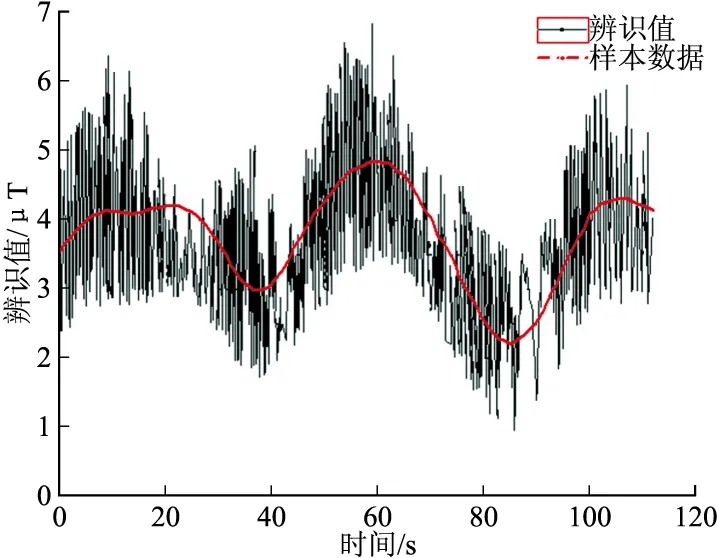
图3 辨识结果

在文中的校正方法中需要用到给定磁场的模值,所以选择了一个模值已知且稳定的磁场。在校正过程中文中选择螺线管式磁场发生设备。该设备内部各点的磁场是恒定的5 μT。还要在螺线管内部固定一个无磁单轴转动平台,将地磁传感器固定在平台上。接收地磁数据并使用文中提出的方法进行校正。校正前后对比如图4所示。

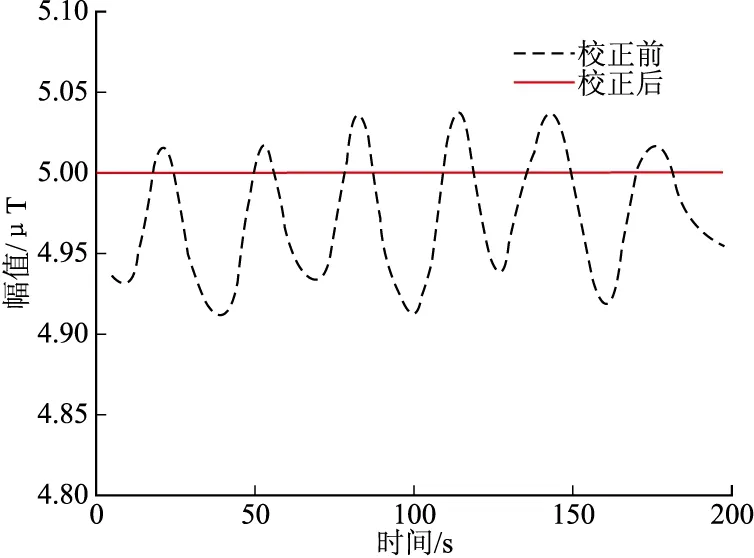
图4 实验结果

4 结论

地磁传感器在模值恒定的磁场中理论上输出模值应该也是不变的,但是由于时变误差原因,由流过电流的变化产生磁场使得传感器输出的模值在一定范围内变化。通过新的校正方法校正后,幅值基本一致,证明该方法有效,可以用于校正时变误差。

[1] 彭富清. 地磁模型与地磁导航 [J]. 海洋测绘, 2006, 26(2): 73-75.

[2] 王广龙, 祖静, 张文栋, 等. 地磁场传感器及其在飞行体姿态测量中的应用 [J]. 北京理工大学学报, 1999, 19(3): 361-363.

[3] T Pylvanainen. Automatic and adaptive calibration of 3D field sensors [J]. Applied Mathematical Modeling, 2008, 32(4): 575-587.

[4] 陈勇巍, 程翔, 张河. 弹道修正弹滚转角测量系统电磁兼容性设计 [J]. 电子测量技术, 2008, 31(1): 43-45.

[5] J M G Merayo, P Brauer, F Primdahl, et al. Scalar Calibration of vector magnetometers [J]. Meas. Sci. Technol, 2000, 11: 120-132.

Calibration with Time-varying Bias for Magnetometer Onboard

HUANG Kun1,TIAN Xiaoli1,WANG Ruihua2,BAI Dunzhuo3,MA Yinghui4,FENG Bingyu2

(1 School of Mechatronics Engineering, North University of China, Taiyuan 030051, China; 2 Jinxi Industries Group Co. Ltd, Taiyuan 030027, China; 3 Yuxi Industries Group Co. Ltd, Henan Nanyang 473000, China; 4 No.208 Research Institute of Chana Ordnance Industries, Beijing 102202, China)

In missiles design process, in order to obtain the dynamic parameters of the missile in flight. We usually use the geomagnetic sensor to measure the attitude information of the projectile. However, there are some errors of three-axis magnetometers which we commonly used. Therefore, the calibration of magnetometers measuring error is seems very important. This article put forward a new method which to calibration the time-varying error of three-axis magnetometers. This method is an expansion for the existing method which is constant error. So that the magnetometer can be used for calibration with time-varying bias. This method is particularly suitable for complex electromagnetic environment onboard measurement system that can effectively calibration the measure error of three axis magnetometer. Finally, the results were verified by simulation data.

ball; magnetometer; time-varying bias; revise

2014-05-07

黄坤(1989-),男,湖北孝感人,硕士研究生,研究方向:兵器工程。

TJ410.6

A