基于粒子滤波的组合定位系统目标跟踪算法*

田安红,杨思源,唐金文,杜衡吉,陆继建,张顺吉,付承彪

(1 曲靖师范学院计算机科学与工程学院, 云南曲靖 655000;2 曲靖师范学院网管中心, 云南曲靖 655000)

基于粒子滤波的组合定位系统目标跟踪算法*

田安红1,杨思源1,唐金文1,杜衡吉1,陆继建2,张顺吉1,付承彪1

(1 曲靖师范学院计算机科学与工程学院, 云南曲靖 655000;2 曲靖师范学院网管中心, 云南曲靖 655000)

因GPS技术在楼群密集的城市不能单独完成定位,文中采用GPS/DTMB组合导航新方案,又针对传统二维机动模型的不足,研究三维下的平面变速转弯模型,并作为运动目标的机动模型,同时仿真对比分析不同粒子数目下的粒子滤波算法(PF)跟踪效果,结果表明,200个粒子的误差均值为4.590 6 m,400个粒子误差均值为2.377 6 m,滤波后的轨迹与真实轨迹基本重合,定位跟踪效果好,且粒子数目越多,误差均值、标准差、方差越小,即定位跟踪精度越高。证明了GPS/DTMB组合导航新方案的可行性。

组合导航;粒子滤波算法;定位跟踪

0 引言

为解决GPS技术在城市楼宇中的定位功能受限问题,室内外导航无缝衔接的连续性、完整性研究日益成为热点。针对被多种定位信号覆盖的都市环境,因数字电视信号具有发射台固定[1]、覆盖范围广、定位精度高、成本低等优点,提出将中国数字电视地面广播(DTMB)信号与GPS信号进行组合导航的无缝定位滤波跟踪方法[2]。该无缝定位方法解决都市环境中单一GPS定位技术的不足。

目前,全世界关于数字电视信号的标准主要有3种[3-6],即美国的ATSC标准、欧洲的DVB标准、中国的DTMB标准。中国的DTMB标准于2006年8月18正式制定并颁布[7],其研究工作处于起步阶段,鉴于DTMB信号定位的优势,迄今,学术界对于DTMB定位技术有着一定的研究[8-9],但对于DTMB与其他定位系统的组合导航研究较少,多数集中在组合导航定位思想的阐述[10-11]。因此,文中针对此情况,深入研究GPS/DTMB组合导航定位系统中的滤波跟踪算法,实现在都市环境中对目标的位置跟踪,进而验证GPS/DTMB组合思想在都市环境中的可行性。

1 GPS/DTMB组合导航定位系统

基于GPS/DTMB的组合定位系统采用伪距法定位。由于DTMB与GPS在系统时间上存在时间差,因此在定位之前对DTMB与GPS系统时间进行同步是关键且必须的。组合定位系统的定位方程为:

(1)

式中:ρi是GPS卫星与用户接收机的伪距测量值;(xi,yi,zi)是GPS卫星的位置坐标;(xu,yu,zu)是用户接收机的坐标;(xD,yD,zD)是DTMB基站的位置坐标;ρD是DTMB信号与用户接收机的伪距测量值;bu是用距离形式表示的GPS系统时间与用户接收机本地时钟的误差;bD是用距离形式表示的DTMB系统与GPS系统的时间差。

2 PF算法

由方程(1)可知,组合定位方程具有非线性特性,文中采用可用于任何动态状态空间模型的非线性滤波算法,即粒子滤波算法(PF),其基本原理过程如下:

非线性系统的状态方程和观测方程的随机状态空间模型为[12-13]:

(2)

其中:xk和yk分别表示系统在k时刻的状态向量和观测向量;uk和vk分别表示状态过程噪声和观测噪声。

PF算法的具体步骤如下:

Step 1 初始化粒子和权值。根据系统噪声的分布函数产生N×l个随机采样点,其中l是状态向量xk的向量维数,N为粒子数目,权值的初始化值为1/N。粒子和权值的集合可表示为:

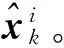
Step 4 权值更新。

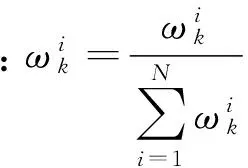
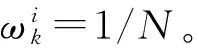
Step 7 估计目标位置。得到xk状态的粒子和权值:

更新状态估计值为:

Step 8 令k=k+1,重复迭代Step2至Step8,能够实现定位跟踪。

3 算法仿真

机动模型主要有:CV/CA模型、Singer模型、“当前”统计模型,这些模型均是在二维平面内推导,为便于仿真,以往学者主要研究二维坐标下的跟踪效果,但实际运动的目标包含X、Y、Z三个方向上的运动状态,为了真实地反应运动特性。文中研究运动目标模型为三维状态下的平面变速转弯模型,其参数衰减系数为0.03,角速度为0.1,仿真时间为100 s,步长为1 s,目标初始位置设定为(0,0,0) m,在X、Y、Z方向的速度分别为6 m/s、-6 m/s、6 m/s,加速度分别为0.4 m/s2、-0.4 m/s2、-0.4 m/s2,距离误差的标准差为6 m,过程噪声服从高斯分布,均值为0,方差为σax=σay=σaz=0.01。

为了验证文中所提及的GPS/DTMB组合导航定位系统的可行性,文中采用PF滤波估计方法进行验证,且选择200个粒子和400个粒子,来观察随着粒子数目的增加PF算法的跟踪效果。定位跟踪轨迹和距离误差如图1和图2所示。

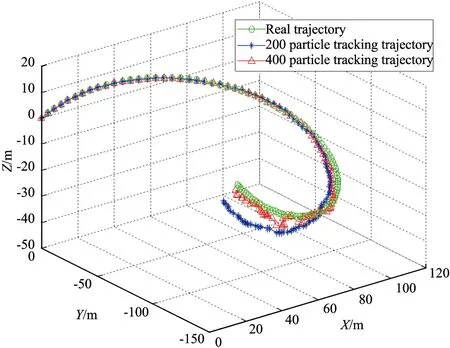
图1 跟踪轨迹

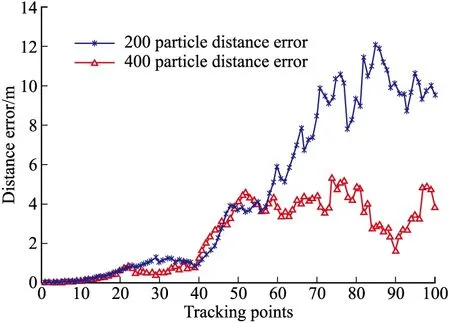
图2 跟踪距离误差

表1 粒子数目定位跟踪误差比较表

图1说明运动目标在三维平面做转弯模型运动时,采用200个粒子和400个粒子的PF算法均能够较好的跟踪目标运动的真实轨迹,跟踪轨迹与真实轨迹基本重合。而定位跟踪距离误差如图2所示,图2说明采用400个粒子的PF算法跟踪精度高于采用200个粒子的PF算法。约从第55个观测点起,400个粒子的PF算法的跟踪误差明显小于200个粒子,400个粒子的误差在0～4 m之间变化,而200个粒子的误差在5～12 m之间变化。

统计分析结果如表1所示,采用200个粒子的PF算法,各个跟踪点的误差均值为4.590 6 m,标准差为4.074 4 m,方差为16.601 4,滤波时间为2.035 6 s。采用400个粒子的PF算法的各个跟踪点的误差均值为2.377 6 m,标准差为1.740 7 m,方差为3.030 0,滤波时间为1.903 7 s。表1说明粒子数目越多,误差均值、标准差、方差越小,即粒子数目的增多伴随着滤波定位跟踪性能的提高。

图1、图2和表1的仿真分析说明,采用PF算法来跟踪运动目标时,粒子数目越多,定位跟踪精度越高,400个粒子的PF算法性能优于200个粒子的性能。

4 结论

文中研究城市环境中GPS/DTMB组合定位新思想,推导粒子滤波算法在组合方程中的实现过程,并采用两组不同的粒子数目来仿真验证PF算法的跟踪效果,结果表明,粒子数目越多,定位精度越高。文中GPS/DTMB组合定位方程具有非线性特性,现有的非线性滤波算法主要有扩展卡尔曼滤波(EKF),Unscented卡尔曼滤波(UKF),平方根Cubature卡尔曼滤波(SCKF)和粒子滤波(PF)等,后续可在文中研究的基础上,进一步对比分析几种非线性滤波算法在不同场景下的定位优势,因此,文中的仿真结果为后续的深入研究奠定了一定的基础。

[1] Linglong Dai, Zhaocheng Wang, Jun Wang, et al. Accurate position location in TDS-OFDM based digital television broadcasting networks [C]∥2010 IEEE 21st International Symposium on Personal Indoor and Mobile Radio Communications, PIMRC 2010: 2621-2625.

[2] Wu Hong, Chen Yao, Zhang Nan, et al. The NLOS error mitigation joint algorithm in hybrid positioning system combining DTMB and GPS [C]∥ 2012 3rd China Satellite Navigation Conference, CSNC 2012: 287-296.

[3] Rabinowitz M, Spilker J. Positioning using the ATSC digital television signal [R]. USA: Rosum Corporation, 2001.

[4] Rabinowitz Matthew, Spilker Jr, James J. Augmenting GPS with television signals for reliable indoor positioning [J]. Journal of the Institute of Navigation, 2004, 51(4): 269-282.

[5] Matthew Rabinowitz, James J, Spilker Jr. A new positioning system using television synchronization signals [J]. IEEE Transactions on Broadcasting, 2005, 51(1): 51-61.

[6] Xianbin Wang, Rahman M J, Sung Ik Park, et al. A new positioning system using DVB-T2 transmitter signature waveforms in single frequency networks [J]. Broadcasting, IEEE Transactions on, 2012, 58(3): 347-359.

[7] 丁涛. NLOS环境下基于DTV信号的定位算法研究 [D]. 南京: 东南大学, 2010.

[8] 阮光俊. 基于数字电视DVB-T的定位系统 [D]. 成都: 西南交通大学, 2009.

[9] 何峰, 吴乐南. 基于数字电视无线广播信号的定位模型和系统 [J]. 东南大学学报: 自然科学版, 2006, 36(5): 690-694.

[10] 李雯琦, 吴虹. 地面数字电视信号与GPS相结合的定位系统 [J]. 电视技术, 2010, 34(6): 11-15.

[11] 田安红, 周非, 付承彪. TV-GPS技术融合实现无缝定位分析技术 [J]. 电视技术, 2009, 33(8): 54-56.

[12] 李善姬, 禹爱兰. 一种改进重采样的粒子滤波算法 [J]. 电讯技术, 2011, 51(9): 35-38.

[13] 陈玲, 陈德煌. 多站无源定位系统中的机动目标跟踪算法 [J]. 电讯技术, 2010, 50(11): 10-14.

Target Tracking Algorithm Research of Integrated Positioning SystemBased on Particle Filter

TIAN Anhong1,YANG Siyuan1,TANG Jinwen1,DU Hengji1,LU Jijian2,ZHANG Shunji1,FU Chengbiao1

(1 School of Computer Science and Engineering, Qujing Normal College, Yunnan Qujing 655000, China; 2 Network Management Center, Qujing Normal College, Yunnan Qujing 655000, China)

In order to overcome deficiency of location functional limitation of GPS in dense building urban areas, this paper adopts the new GPS/DTMB integrated navigation scheme, in view of the shortcomings of traditional two-dimensional dynamic modelthis paperthe planar variable-turn model under dimensional model, which is used as moving target maneuvering model, also, simulation the tracking effect under different particle numbers of 200 and 400 of particle filter(PF) algorithm, theoretical analysis and simulation results show that mean error of 200 particles is about 4.590 6 m, 400 particles is about 2.377 6 m, the filtering trajectory is consistent with the real trajectory basically, which has good location tracking effect, and the more particle numbers, the smaller mean error, standard deviation, variance, the smaller the error of the mean, standard deviation, variance, this means that location tracking precision is higher. These proved the feasibility of GPS/DTMB integrated navigation.

integrated navigation; particle filter algorithm; location tracking

2014-07-14

云南省科技厅青年项目(2014FD048);云南省教育厅科学研究基金(2013Y017);曲靖师范学院校级青年项目(2011QN018)资助

田安红(1984-),女,贵州安顺人,讲师,硕士,研究方向:无线定位导航。

TN96

A