自导深弹中自导与引信系统的Bayes可靠性鉴定试验方案*

袁志勇,陈宜辉

(海军工程大学兵器工程系,武汉 430033)

自导深弹中自导与引信系统的Bayes可靠性鉴定试验方案*

袁志勇,陈宜辉

(海军工程大学兵器工程系,武汉 430033)

为了对自导深弹的自导与引信系统进行可靠性鉴定,文中建立了Bayes可靠性决策模型,运用金字塔方法,提取了该系统可靠性的先验信息,并以抽样净益(ENGS)最大为准则,制定了自导与引信系统的可靠性鉴定试验方案。从实例计算结果来看,按照文中的方法得到的可靠性鉴定试验方案是合理的、可行的,比国家军用标准中所规定的方案分别节省时间36.55%和17.45%。

自导深弹;Bayes决策;可靠性;鉴定试验

0 引言

在自导深弹的可靠性鉴定试验中,自导与引信系统的鉴定试验是一项重要工作。根据自导与引信的工作原理及使用经验,自导与引信系统的寿命通常服从指数分布。自导与引信系统的鉴定试验方案通常可选用国家军用标准中推荐的试验方案进行,但是利用该方案需要专门加工较多的试验样机,进行较长时间的试验,使得鉴定费用占整个研制费的很大比例。由此可见,对于技术复杂并且造价高的自导与引信系统,需要寻求一种新的方法。

由于其试验样本量很小,采用系统自身的数据进行系统可靠性鉴定存在困难。为了利用系统组成单元的试验数据以求得系统可靠性鉴定试验方案,采用了系统可靠性综合的方法[1]。它的基本思想就是把系统组成单元的试验数据折算成系统的等效数据,由系统自身的少量数据与系统的等效数据共同构成系统的综合数据,从而扩大了系统的样本量,使Bayes理论在可靠性鉴定问题上的应用成为可能。

1 自导与引信系统可靠性的先验信息

由于自导与引信系统研制中包括原理样机、第一初样、第二初样和正样的几个阶段,均需要进行可靠性试验,因此可以得到一定的可靠性信息。另外,自导与引信系统的分系统需要进行大量的可靠性试验,可以得到较多组试验数据。根据金字塔方法(MML),自导与引信各个分系统试验信息可以综合成系统试验数据[2]。设第i个分系统的试验数据为(ri,τi),则n个分系统试验信息折合成相当于整个系统试验的总时间为:

(1)

同样,n个分系统试验信息折合成相当于整个系统试验的故障数为:

(2)

根据以上试验信息,由可靠性增长方法或分位点方法[3-4],就可以来确定正样阶段自导与引信失效率λ的先验分布:

(3)

自导与引信系统的可靠性鉴定试验的具体步骤是:从N件正样中任意抽取n件做定时(t0)有替换截尾试验,记总试验时间T=nt0,并观察试验中的样品失效数r。若样品失效数r不超过合格判定数c,则该系统通过鉴定,否则未能通过[5]。其间样品失效数r服从Poisson分布:

(4)

这样可以得到失效率λ的后验分布为:

(5)

根据式(4),可以得到在抽样试验中的样品失效数r的边缘分布D(r),即:

2 Bayes可靠性鉴定试验方案的数学模型

假定样品失效率的极限值为λ0,则决策损失函数[6]可定义为:

(7)

其中:α1表示决策者认为该系统通过鉴定,α2表示决策者认为该系统不能通过鉴定;c1、c2分别表示使用方和研制方所受的相对损失值,可根据使用方和研制方的实际情况来确定。

如果决策者在采取行动之前,除了先验信息以外没有得到任何抽样信息,那么决策者仅仅依靠样品可靠性的先验信息所采取的最优行动α*满足:

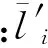
(9)

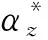
(10)

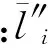
i=1,2

(11)

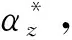
(12)

因为在抽样试验中样品失效数r为任意一个不大于抽样数n的整数,所以抽样信息期望值为:

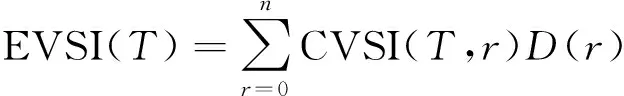
(13)

根据抽样试验信息z=(T,r),总的抽样试验费用l(e,z)可以定义为:

l(e,z)=k1r+k2T

(14)

其中:k1表示每单位样品的成本或维修费用;k2表示每单位时间内样品进行抽样试验所需的观察费用和试验费用。因此,抽样信息期望费用ECSI为:

(15)

根据式(13)、式(15),可以得到决策者在进行了抽样试验e后所得的抽样净益为:

ENGS=EVSI(T)-ECSI(T)

(16)

从式(16)可以看出,抽样净益ENGS为一组数值。因此,可以求出使抽样净益ENGS达到最大的总试验时间T*,并由式(10)可知,若式(17):

(17)

成立,则选择行动α1。式若(17)不成立,则选择行动α2。根据式(17)可以得到产品失效数r的一组值,令其中最大值为合格判定数c。因此,可以得到Bayes可靠性鉴定试验方案为(T*,c)。

3 算例

假定自导与引信系统的样品批量数N=50,该系统的极限设计寿命θ0为56 900 h,即失效率的极限值λ0=1.758×10-5。定时有替换截尾试验中t0取为5 016 h。根据该系统的实际情况,损失函数中c1、c2、k1、k2分别取值为1亿元,0.45亿元,0.003亿元,5.98×10-8亿元。根据分位点的方法[3],由该系统的先验信息可以确定出先验参数a=0.835、b=11 436.715。

根据式(16)和式(17),通过计算程序可以得到自导与引信系统的Bayes可靠性鉴定试验方案为(140 448,1),即50件正样中任意抽取28件样品进行定时有替换截尾试验,在总试验时间140 448 h内,若产品失效数不大于1,则该系统通过鉴定;若产品失效数大于1,则该系统不能通过鉴定。此时,抽样净益ENGS与总试验时间T的函数关系如图1所示。从图1可以看出,当总试验时间T=140 448 h时,抽样净益ENGS的最大值为0.025 9亿元。

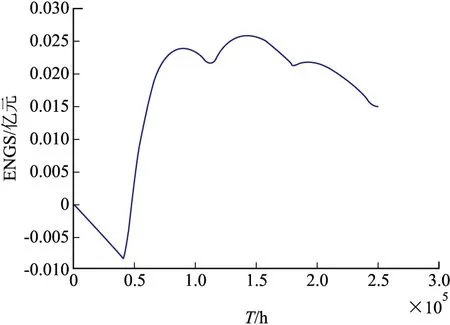
图1 抽样净益ENGS与总试验时间T的函数关系

若按照GJB899A-2009进行鉴定试验,使用方风险分别取10%和20%,则可靠性鉴定试验方案分别为(3.89×θ0,1)、(2.99×θ0,1)[9],即(221 341,1)、(170 131,1)。可以看出,文中的Bayes鉴定试验方案比国家军用标准中所规定的方案分别节省时间36.55%和17.45%。

4 结束语

文中建立了Bayes可靠性决策模型,以抽样净益(ENGS)最大为准则,制定了自导深弹中自导与引信系统的可靠性鉴定试验方案。从实例计算结果来看,按照文中的方法得到的可靠性鉴定试验方案是合理的、可行的,比国家军用标准中所规定的方案分别节省时间36.55%和17.45%。文中的研究方法同样可以应用于其它武器装备的可靠性鉴定试验。

[1] 蔡洪, 张士峰, 张金槐. Bayes试验分析与评估 [M]. 长沙: 国防科技大学出版社, 2004.

[2] 陈宜辉. 小子样验证技术及其在武器装备上应用 [D]. 武汉: 海军工程大学, 2002.

[3] 张志华, 姜礼平. 指数型产品失效率鉴定试验的Bayes方案 [J]. 应用概率统计, 2000, 16(1): 66-70.

[4] 姜礼平, 张志华. 成败型产品成功率鉴定试验的一种Bayes方法 [J]. 工程数学学报, 2000, 17(4): 25-29.

[5] 陈宜辉, 王树宗. 火箭深弹贮存可靠性验证的一种贝叶斯方法 [J]. 弹箭与制导学报, 2003, 23(2): 154-155.

[6] 陈珽. 决策分析 [M]. 北京: 科学出版社, 1997.

[7] Papazoglou I A. Bayesian decision analysis and reliability certification [J]. Reliability Engineering and System Safety, 1999 (66): 177-198.

[8] 姜礼平, 陈宜辉. 基于抽样净益的成败型产品Bayes鉴定试验方案 [J]. 系统工程, 2002, 20(6): 91-93.

[9] GJB899A-2009 可靠性鉴定与验收试验 [S]. 北京: 中国人民解放军总装备部, 2009.

A Bayesian Plan of Reliability Verification Test about Homing and Fuse System of Homing Depth Charge

YUAN Zhiyong, CHEN Yihui

(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)

In order to verify the reliability of homing and fuse system of homing depth charge, the mathematics model of Bayes reliability decision is established in this paper. The prior information of this system reliability is extracted according to MML, and then the plan of reliability verification test about homing and fuse system is worked out in terms of maximum ENGS. In view of the result of example calculation, the plan of reliability verification test obtained according to the method of this paper is reasonable and feasible, and saves the time of 36.55 percent and 17.45 percent respectively compared to the plan of national military standard.

homing depth charge; Bayesian decision; reliability; verification test

2014-04-02

袁志通(1965-),男,江苏丹阳人,教授,研究方向:深弹反潜技术、反鱼雷技术、武器系统对抗技术。

TJ650.1

A