滚珠丝杠副空回程角的研究
2015-05-07朱自清吴柯锐侯文李建民张博川
朱自清, 吴柯锐, 侯文, 李建民, 张博川
(1.中北大学a.仪器科学与动态测试教育部重点实验室,b.机械与动力工程学院,太原030051;2.空军驻山西地区军事代表室,太原030024)
0 引言
滚珠丝杠副是一种高效、精密的定位传动部件,目前已广泛地应用于数控机床、航空航天、半导体制造等行业。滚珠丝杠副在工作过程中,由于轴向载荷的施加,使得滚珠和滚道发生弹性变形,导致滚珠丝杠副在换向工作的过程中会产生一定的滞后,在滚珠丝杠副中用空回程角来描述。空回程角的存在,造成了滚珠丝杠副轴向定位的误差,会对滚珠丝杠副的性能产生影响。之前已有相关学者对滚珠丝杠副空回程角的问题进行了研究,刘建佐等[1]在研究滚珠丝杠副的空回程角的问题时,从理论上论述了空回程角的产生原因和影响因素,但并未推导出具体的计算公式;姜洪奎等[2]研究了滚珠丝杠副的弹性变形,得到了滚珠丝杠副弹性变形和各项参数之间的关系,但并未对空回程角和弹性变形之间的关系加以说明。本文在现有研究成果的基础上,通过赫兹接触理论从理论上推导出空回程角的计算公式,给出了空回程角和螺旋升角、接触角以及载荷分布系数之间的关系;最后以2004-3型滚珠丝杠副为算例,在轴向力为100 N的情况下对其空回程角进行了理论计算,并通过和有限元分析软件ANSYS的仿真结果进行比照,验证了结论的正确性。
1 滚珠丝杠副中空回程角和螺旋升角、接触角、载荷分布系数之间的关系
在滚珠丝杠副的工作过程中,在运动方向未发生改变的情况下,由于轴向力的作用,滚珠和滚道之间会发生弹性变形;当运动方向突然改变时,之前所发生的弹性变形先是减小到零,然后再一次在滚珠和滚道之间发生弹性变形,在这些动作完成之后,丝杠和螺母的运动才会相协调。在这个过程中所产生的弹性形变,正是产生空回程角的真正原因,所以接下来就先分析一下在换向过程中发生的弹性形变。
1.1 滚珠的受力分析
滚珠在运动的过程中,主要受到沿滚道切向的摩擦力和沿滚道法向的力,而和弹性变形有关的只是法向力,所以我们在下面的内容中主要分析法向力。滚珠作为滚珠丝杠副传动的中间元件,各个滚珠受到的力不同,也就是说工作载荷的分布是不均匀的,为了分析方便,假设滚珠受到的载荷是沿着螺旋滚道呈比例递减的。设初始滚珠受到的法向载荷为P0,滚珠所承受的载荷衰减系数为α,则第i个滚珠受到的法向载荷Pi=αi-1P0。所以,总体滚珠的法向载荷与螺母受到的轴向推力Fa之间的关系为
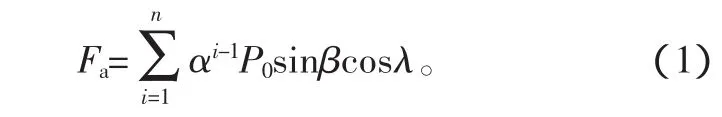
式中:λ为螺旋升角;β为滚珠与滚道接触角。由于α<1,所以式(1)可写为
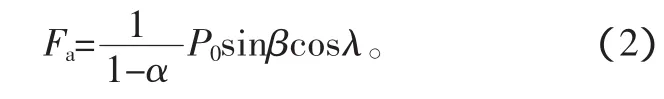
1.2 滚珠和滚道发生的弹性形变
根据赫兹接触理论,在法向载荷的作用下,滚珠和滚道的接触处发生弹性变形(包括滚珠的变形和滚道的变形),其法向弹性变形的计算公式如下[3]:

式中,μ1、μ2及 E1、E2分别为滚珠和丝杠材料的泊松比和弹性模量;∑ρs、∑ρp分别表示螺母侧和丝杠侧滚道的主曲率之和;αs、αp分别为螺母侧和丝杠侧的载荷分布系数,Js、Jp是由赫兹接触参数τ确定的椭圆积分。
其中,滚珠与螺母滚道接触点处的4个主曲率[4]分别为

同理,滚珠与丝杠侧滚道接触点处的4个主曲率分别为
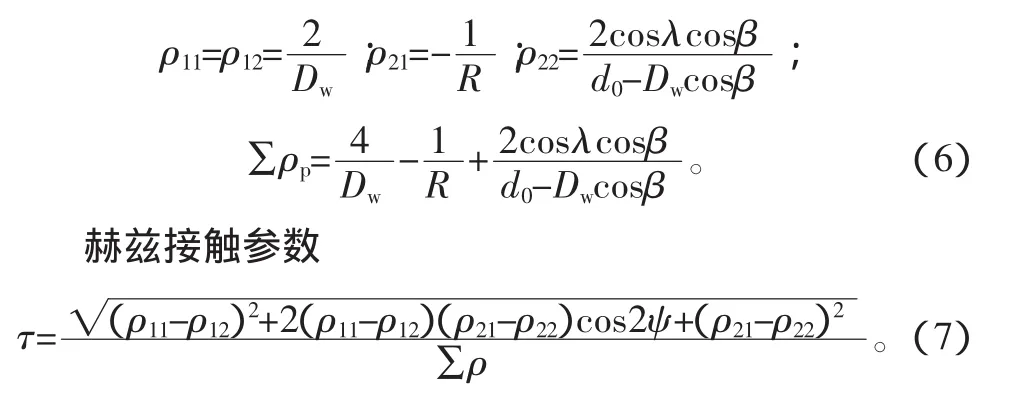
式中,ψ为接触体主平面方向和接触椭圆长半轴的夹角。由于接触体滚珠为球体,所以ρ11=ρ12,上式可简化为
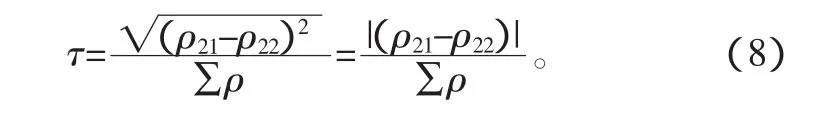
因为J为由τ确定的椭圆积分,所以在得出τ之后,通过查询椭圆积分表[5]可得出J的值。
因为空回程角的存在会对滚珠丝杠副的轴向定位产生影响,所以将滚道的法向弹性位移投影到丝杠轴向上,得到丝杠的轴向弹性位移,设其值为δa,则

1.3 换向过程中产生的空回程角
以上分析的是在运动方向发生改变之前,当运动方向发生改变之后,滚珠和滚道所发生的弹性变形也是δa,所以在产生空回的过程中,轴向弹性变形为2δa,也就是说丝杠和螺母相对运动2δa之后才进行同步的传动。所以在这个过程中产生的空回程角为

2算例
为了证明滚珠丝杠副弹性变形模型的正确性,通过理论计算和有限元仿真两种方法对其进行验证。以2004-3型滚珠丝杠副为例,其各项参数为:丝杠公称直径d0=20 mm,丝杠导程Ph=4 mm,滚道(双圆弧滚道)半径R=2.08mm,滚珠直径Dw=2.381 mm。滚珠承载载荷的衰减系数 α=0.8,载荷分布系数 αs=αp=0.85,接触角 β=45°,丝杠、滚珠和螺母的材料均为轴承钢,丝杠和螺母的弹性模量E1=2.06×105MPa,泊松比 μ1=0.3;滚珠的弹性模量 E2=2.1×105MPa,泊松比μ2=0.3;所受的轴向力Fa=100 N。
2.1 滚珠丝杠副空回程角的理论计算结果
该型滚珠丝杠副的导程Ph=4 mm,所以其螺旋升角可以通过下面的公式来计算:
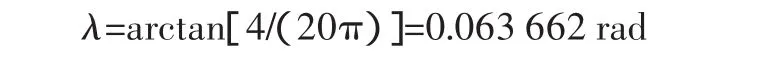
通过所给参数进行计算,可得滚珠与丝杠滚道接触点处的 4 个主曲率及主曲率之和为:ρ11=ρ12=839.9832m-1;ρ21=-480.769231m-1;ρ22=65.376532m-1;∑ρp=1264.573701m-1。
同理,滚珠与螺母滚道接触点处的4个主曲率及主曲率之和为:ρ11=ρ12=839.983 2 m-1;ρ21=-480.769 231 m-1;ρ22=-55.224 232 m-1;∑ρp=1 143.972 937 m-1。
根据主曲率及主曲率之和的值,得出赫兹接触参数,继而查找椭圆积分表,得:Js=1.629 480;Jp=1.652 514。
将滚珠丝杠副的各项参数带入式(13)中,得到空回程角的理论值:δa=0.33×10-4m;θ=0.103 613 rad。
2.2 滚珠丝杠副弹性变形的有限元分析
在滚珠丝杠副模型中,涉及到了滚珠和滚道的接触,而接触问题作为一种边界非线性问题,接触边界随载荷非线性变化是其难点,因此根据滚珠丝杠副的结构特点,将其简化成只有单个滚珠的模型,并且选用Solid45作为它的单元类型,其他参数保持与理论计算参数一致,建立了滚珠丝杠副的有限元模型。
在建立了滚珠丝杠副的有限元接触模型之后,对其进行接触对的添加。因为在实际工作的过程中,滚珠和滚道的接触是点接触,所以我们在建模的过程中也选用点接触。关于目标面和接触面的选定,我们选择滚珠表面作为目标面,滚道作为接触面。建立接触对的过程中,摩擦因数设定的是0.02。在接触对建立好之后,对其进行加载,给丝杠滚道的下边线和螺母滚道的上边线各施加一个Y方向的位移约束,防止其在受力时发生Y方向的移动;在丝杠侧和螺母侧各施加100 N的恒力(此处须生成一个关键点,便于力的施加);对滚珠不作任何约束。然后对其进行求解,求解完成后的结果如图2所示。
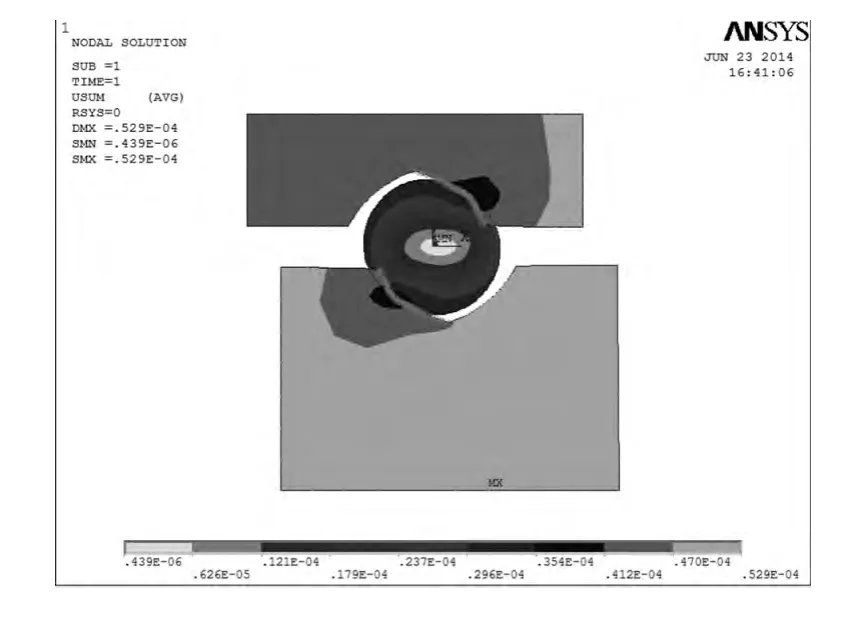
仿真结果显示滚珠丝杠副在受到100 N的轴向力时,由于滚珠和滚道挤压所产生的弹性变形δa=0.354×10-4m,产生的空回程角为0.111212rad,与理论计算值0.103613rad接近,验证了所建立模型的正确性。
3 结论
本文利用矢量几何学的方法,描述了滚珠丝杠副中滚珠和滚道接触点的运动;利用赫兹接触理论,提出了滚珠丝杠副中空回程角的理论计算公式,并且利用有限元分析软件ANSYS进行了仿真,和理论计算结果进行对比,对工程实践中空回程角的确定有一定的帮助。
[1] 刘建佐,张成义,王向东.滚珠丝杠副空回程角研究[J].组合机床与自动化加工技术,2010(12):1-4.
[2] 姜洪奎,宋现春,张佐营.螺旋升角对滚珠丝杠副弹性变形的影响分析[J].中国机械工程,2008,19(9):1079-1083.
[3] 宋现春,姜洪奎,许向荣,等.高速滚珠丝杠副弹性变形的有限元分析[J].北京工业大学学报,2009,35(5):582-586.
[4] 李凌丰,刘彩芬.滚珠丝杠副轴向变形分析[J].中国机械工程,2011,22(7):762-766.
[5]《椭圆积分表》编写小组.椭圆积分表[M].北京:机械工业出版社,1979:295.
