国家层面综合客运枢纽分层布局鲁棒优化模型

李婷婷 宋 瑞

(1北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044)(2北京交通大学交通运输学院,北京100044)

国家层面综合客运枢纽分层布局鲁棒优化模型

李婷婷1宋 瑞2

(1北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044)(2北京交通大学交通运输学院,北京100044)

为提高国家层面综合客运枢纽的运行效率,充分分析枢纽等级和需求层次的对应关系,考虑城镇化发展阶段客运需求的不确定性,构建了基于有能力限制的层级选址模型和随机p-鲁棒(p为相对后悔值限定系数)的综合客运枢纽布局优化模型.设计免疫克隆算法对模型进行求解,通过算例验证模型和算法的有效性.结果表明:分层布局方法比非分层布局方法更优,当p小于分层随机优化模型所有情景中的最大相对后悔值时,分层鲁棒优化模型求解结果的鲁棒性比分层随机优化模型更强,设计的算法比优化软件CPLEX更高效,同时p的取值、枢纽覆盖范围和情景概率对枢纽布局方案产生较大影响.分层鲁棒优化模型能为国家层面综合客运枢纽布局提供决策参考.

交通运输系统工程;布局优化;层级选址模型;综合客运枢纽;鲁棒优化;免疫克隆算法

合理的综合客运枢纽布局对构建高效的综合运输体系、提升客运服务水平、促进城镇化发展有重要的现实意义.国家层面综合客运枢纽布局规划是战略性问题,研究不同等级枢纽节点城市的选取,属于分层设施选址问题.同时,我国近年来大规模的城镇化进程使客运需求的不确定性进一步加剧,故该问题属于不确定的分层设施选址问题.国外针对分层设施选址问题提出了层级选址模型[1-6],并广泛应用于医疗卫生、产品布局、教育系统、通信网络等方面,但考虑不确定性的分层设施选址问题研究较少[7-8],而结合鲁棒优化的分层设施选址模型更为鲜见.国内对国家层面综合客运枢纽规划布局的研究主要有节点重要度法[9]、数学优化模型[10-12],这些方法没有体现不同等级枢纽和不同层次需求之间的关系,同时缺乏对城镇化发展背景下客运需求不确定性的考虑.

针对上述问题,本文按照“客流分层,枢纽分级,分层布局”的思路,构建国家层面综合客运枢纽布局优化模型，以制定鲁棒性强的布局方案满足规划年限内客运的需求,为省级层面综合客运枢纽布局规划提供正确指导.

1 国家层面综合客运枢纽布局规划

1.1 目标和特点

综合客运枢纽布局规划分为国家层面、省级层面、城市层面3个层次.国家层面规划作为顶层规划,即在国家综合运输网络的基础上,结合城市的人口规模、经济发展及其在国家综合运输网络中的地位和功能,选择重要节点城市作为综合客运枢纽,以满足国家生产力战略布局和促进区域一体化发展.此层面综合客运枢纽布局规划是战略性问题,主要确定枢纽节点城市及其交通功能,不涉及具体场站的选址问题.

目前,我国正处在城镇化快速发展时期,国家层面综合客运枢纽布局规划具有如下特点:① 由于经济发展和交通运输方式变革的影响,客运需求呈现层次性.因此,国家层面综合客运枢纽应具有合理的等级结构,根据客流需求进行分层布局,以更好地为不同层次的需求服务.② 由于城镇化进程中客运需求具有不确定性,在枢纽布局规划前期难以对其进行精确预测,枢纽布局规划时应加以考虑.

1.2 建模思路

根据国家层面综合客运枢纽布局规划的特点,在建模时,首先分析不同层次客运需求与不同等级枢纽的对应关系,应用层级选址模型描述这种关系.对于城镇化进程中客运需求的不确定性,结合不确定优化方法——随机p-鲁棒优化方法进行处理.

1) 不同层次客运需求与不同等级枢纽的对应关系.层级选址模型[2]按照服务属性可划分为嵌套型和非嵌套型,嵌套型层级系统的高等级设施提供低等级设施的所有服务和至少一种额外服务；而非嵌套型系统中各等级设施提供不同的服务.由表1中各等级枢纽对应的服务客流可知,国家层面的综合客运枢纽系统属于嵌套型层级系统,建模时采用嵌套型层级选址模型描述不同层次客运需求与不同等级枢纽的对应关系.

表1 综合客运枢纽等级及其对应服务客流

2) 客运需求不确定性的处理.不确定性优化方法主要有两类:随机优化和鲁棒优化.随机优化一般以最小化期望成本为目标函数,能得出平均期望成本最小的方案,但有时会出现部分情景下方案较优而某些情景下方案较差的情况.同时,随机优化依赖于不确定参数的概率分布,而这种分布往往难以获取.鲁棒优化中不确定参数对应离散的情景或连续区间,一般以最小化最大成本或后悔值为目标函数.然而,典型的鲁棒优化方法过于保守,虽能避免最坏情况的发生,但最坏情况发生的概率却很低.

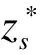
随机p-鲁棒优化模型为

(1)

(2)

式中,qs为情景s发生的概率；Ω为可行解空间.

综上所述,本文借鉴随机p-鲁棒优化方法处理城镇化进程中客运需求的不确定性.

2 国家层面综合客运枢纽分层布局鲁棒优化模型

首先作以下假设：需求点和备选枢纽点同在城市的中心;同一需求点同一层次需求分配到同一枢纽;一定时期内各等级枢纽覆盖范围为确定值.除了考虑综合客运枢纽与客运需求的对应关系及需求不确定性,模型对枢纽不同层次服务能力加以约束,即所有枢纽提供任何层次服务的能力均有限,枢纽承担的各层次交通需求均应在枢纽各层次服务的最大能力范围内,而由于枢纽功能有所侧重,只要求其承担的最高层需求量超过相应值,对其承担的低层次服务量不作最小能力限制.分层布局(HR)模型为

(3)

(4)

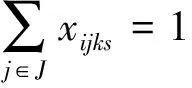
(5)

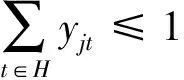
(6)

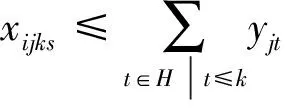
(7)

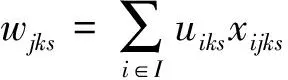
(8)

wjks≥bjkyjt∀j∈J,t∈H,

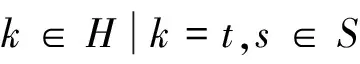
(9)

(10)

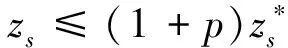
(11)

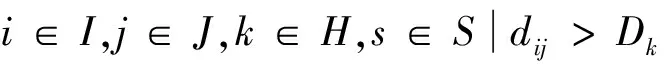
(12)

(13)

式中,H表示需求点的需求层次、枢纽点的服务层次和枢纽等级的集合,H={1,2,3};I为需求点集合;J为所有备选枢纽点集合；k为需求点的需求层次和枢纽点的服务层次；t为枢纽等级;dij为需求点i和枢纽点j间的距离;uiks为情景s下需求点i第k层的需求量;bjk为若在枢纽点j设立枢纽,该枢纽点承担的第k层需求量至少达到的值(下文称为服务能力最小值);Bjk为枢纽点j能提供的第k层服务的最大能力(下文称为服务能力最大值);Dk为第k层需求用户能接受的需求点到枢纽的最远出行距离；yjt为如果枢纽点j被选中为t级枢纽,则yjt=1,否则为0;xijks为情景s下如果需求点i第k层需求由枢纽点j服务,则xijks=1,否则为0;wjks为情景s下枢纽点j承担的第k层需求量.

式(3)表示所有情景的期望需求加权距离最小化;式(4)表示情景s下的需求加权距离;式(5)表示任何情景下所有需求点任何层次的需求都得到满足;式(6)表示任何枢纽点都不允许同时设立不同等级的枢纽;式(7)表示任何情景下需求点任一层次的需求必须由相同或更高等级的枢纽服务(1级为高级,3级为低级);式(8)表示任何情景下枢纽承担的任一层次的需求量等于由该枢纽点服务的所有需求点的对应层次的需求量之和;式(9)表示任何情景下枢纽承担的最高层次的需求量必须大于等于该枢纽点最高层次服务能力最小值;式(10)表示任何情景下枢纽承担的任一层次的需求量必须在其对应层次服务的最大能力范围内;式(11)为鲁棒约束,表示任何情景下的需求加权距离不超过对应最优解的100%p;式(12)表示任何情景下如果需求点到枢纽点的距离在可接受范围之外,需求点不由该枢纽点服务;式(13)表示变量的取值范围约束.

3 模型求解

3.1 模型分析

不考虑约束(11):对给定的情景s,模型HR的需求参数为确定值,其实质为确定性分层优化(HD)模型;对给定的情景集S,模型HR实质为如下基于情景的分层随机优化(HS)模型：

s.t. 式(5)～(10)、(12)和(13)

3.2 免疫克隆算法

对于大规模、多情景问题,使用免疫克隆算法求解.算法设计如下:

1) 编码方案.采用二进制编码,每个抗体由3部分组成,每部分表示为各需求点某层次需求服务的枢纽点编号,抗体长度为需求点数量与需求层次总数的乘积.如图1所示,圈中数字表示编号为1的需求点的1级需求由编号为0的枢纽点服务,而其2级和3级需求均由编号为1的枢纽点服务.另外,从抗体可以判断枢纽的等级:为1级需求服务的枢纽点是1级枢纽;为2级需求服务的枢纽点,如果同时出现在1级需求部分,则为1级枢纽,否则为2级枢纽;为3级需求服务的枢纽点,如果同时出现在1级需求部分,则为1级枢纽,如果同时出现在2级需求部分而不出现在1级需求部分,则为2级枢纽,仅在3级需求部分出现的为3级枢纽.

图1 免疫克隆算法编码方案

2) 初始化.首先进行数据预处理,根据要求(需求点在枢纽点覆盖范围内,且枢纽点能提供相应层次服务)筛选出能为各需求点各层次需求服务的枢纽点集合,然后从集合中随机选取任一枢纽编号生成抗体.

3) 亲和度函数.同时考虑约束(9)～(11),采用罚函数法,将约束合并到目标函数中,以δ1，δ2，δ3为惩罚因子,亲和度函数为

4) 克隆个数、变异概率、选择个数、变异操作.每个抗体的克隆个数与其亲和度成正比；变异概率、选择个数为迭代次数的函数,随着迭代次数增加,变异概率变大,选择个数变少；变异操作为抗体每部分各自按单点变异法进行,具体可见文献[14].

5) 算法终止条件.当最优值连续迭代若干次不再变化或者迭代次数达到最大迭代次数M时，终止运行.

算法步骤如下:

① 数据预处理和初始化.随机产生N个抗体,组成初始抗体群P.

② 根据亲和度函数计算亲和度.根据亲和度值从大到小进行排序.

③ 对抗体种群中的抗体进行克隆扩增操作,得到扩增后的抗体群C.

④ 对抗体群C中的抗体进行高频变异,得到C*.

⑤ 从C*中选择d个亲和度高的抗体，替换P中d个亲和度低的抗体.

⑥ 判断终止条件是否满足,如果满足，则程序结束并输出最优解,否则转至③.

4 算例

4.1 算例设计

下面设计算例对模型和算法进行验证,图2为研究区域及其路网.

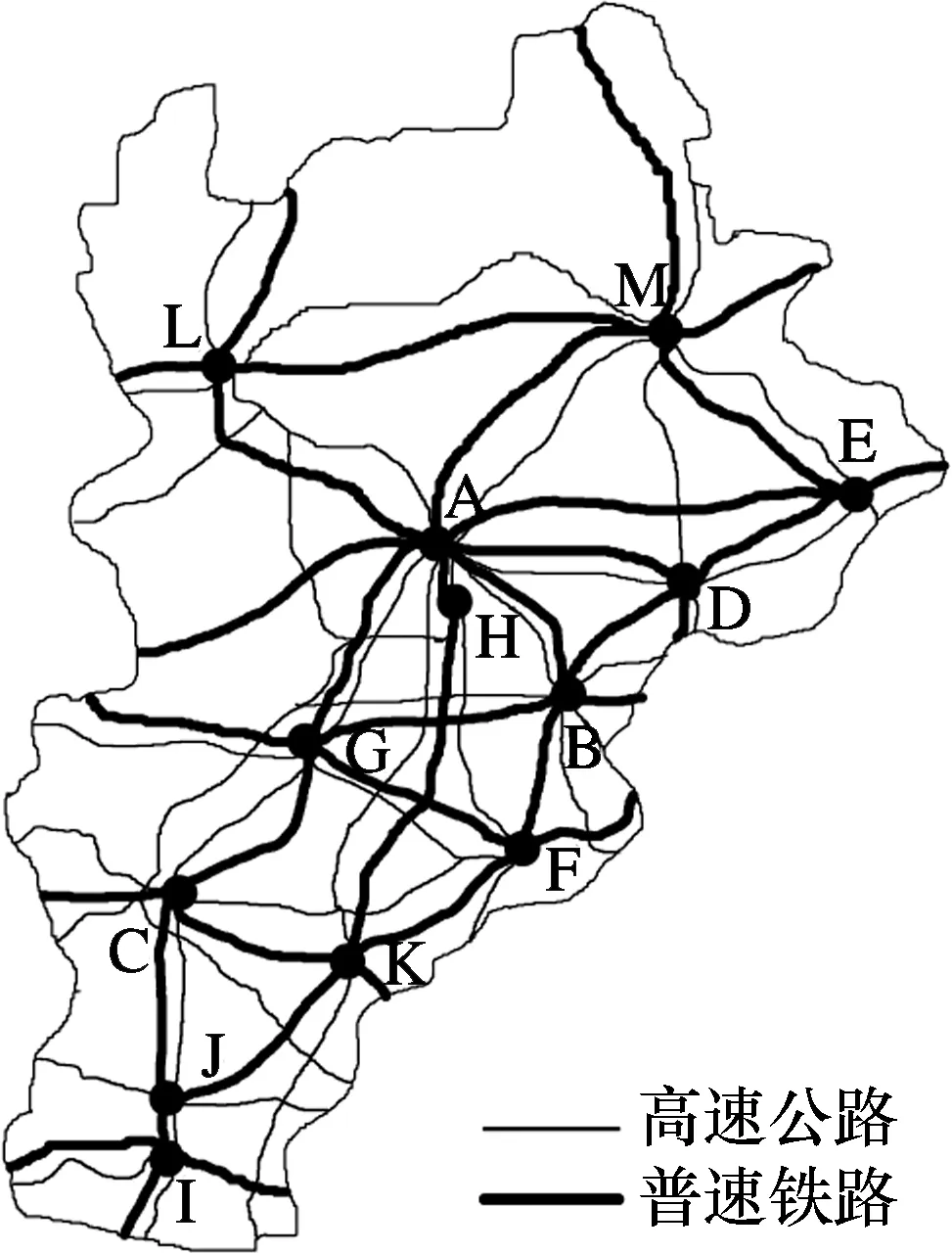
图2 研究区域需求点分布及路网图

图2中,城市A～城市M为需求点,城市A～城市E为1级枢纽备选点,城市A～城市I为2级枢纽备选点,城市A～城市M为3级枢纽备选点,1、2、3级枢纽覆盖范围分别为600,300,100 km.各城市间距离如表2所示,各城市服务能力最小值相同,1、2、3级分别为6 000,5 000,3 500万人次/a,服务能力最大值如表3所示.设计10个情景，每个情景对应不同需求.表4为情景1需求,其他情景需求依此按5%的比例增长,各情景概率均为0.1.

4.2 结果分析

在Intel Core I5-2450M CPU@2.50 GHz,内存2 GB,Visual Studio 2008平台上调用优化软件CPLEX12.2对模型HD求解,同时编程实现免疫克隆算法对模型HR进行求解.其中运行参数设置为:初始种群规模为100,克隆个数最大值为15,克隆个数最小值为5,变异概率最大值为0.8,变异概率最小值为0.1,变异概率常数为0.8,最大迭代次数为1 000,或连续迭代50次不变化则终止,δ1,δ2均取10 000,δ3取10.

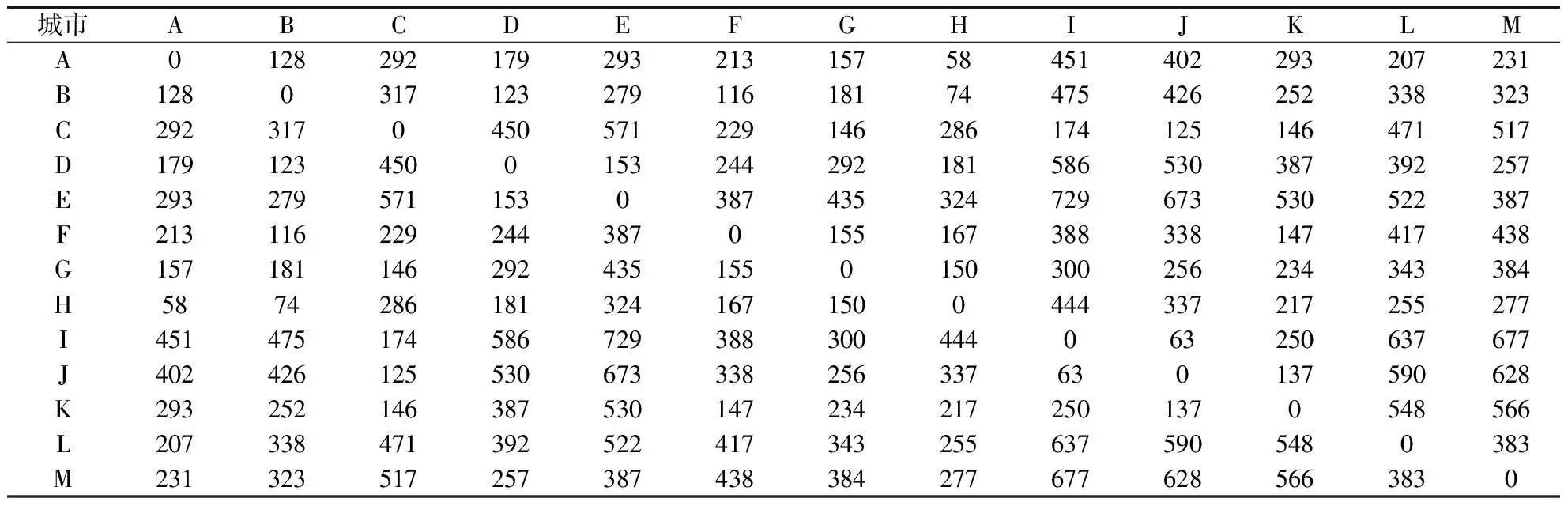
表2 城市之间的距离 km

表3 城市各层次服务能力最大值 万人次/a

表4 城市各层次需求(情景1) 万人次/a

4.2.1 算法分析

如表5所示,当p≥0.12时,免疫克隆算法求解得到的目标函数值比采用优化软件CPLEX求解得到的值大,但相对偏差不超过5%,说明该情况下免疫克隆算法求解结果是有效的,而由于软件CPLEX求解时间远小于免疫克隆算法,故该情况下采用软件CPLEX求解更为适用.当p<0.12时,使用CPLEX求解由于内存不足而停止运算,此时得到的上下界与免疫克隆算法的相对偏差均小于4%.因此,当p<0.12时,免疫克隆算法目标函数值与最优目标函数值更接近,且免疫克隆算法的求解时间短得多,故该情况下使用免疫克隆算法求解具有更明显的优势.

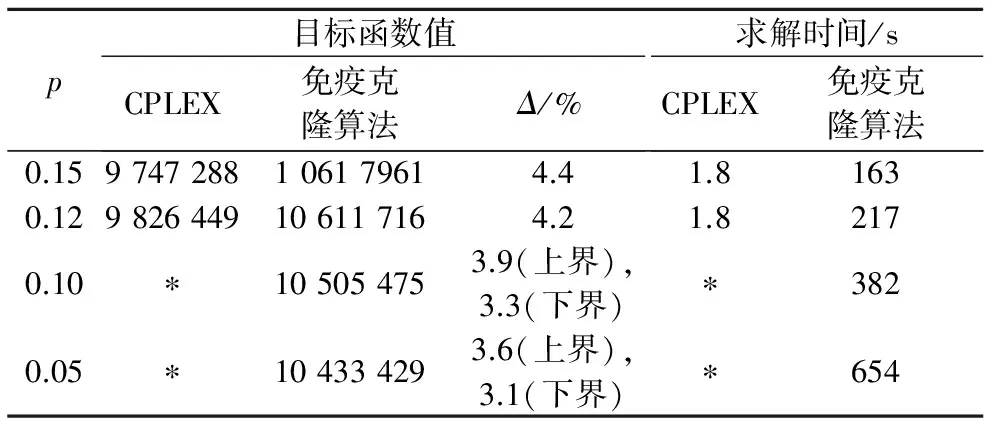
表5 免疫克隆算法与CPLEX的比较

注：Δ表示使用免疫克隆算法求解得到的目标函数值与使用软件CPLEX求得值的相对偏差;*表示由于内存不足停止运算.

4.2.2 不同模型求解结果的比较

如表6所示,当p=0.15时模型HR的目标函数值比模型HS的目标函数值大；当p=0.12时，两模型的目标函数较为接近；而p=0.1或0.05时,模型HR的目标函数值均比模型HS小.原因可以从表7看出,由于所有情景下模型HS对模型HD的相对后悔值均低于12%,若模型HR中p>0.12,某些情景的相对后悔值比模型HS的大,从而导致模型HR的目标函数值更大.此外,从表6看出,当p≥0.12时,模型HS和HR求得的枢纽布局方案相同,当p=0.1或0.05时,模型HR与模型HS求得的布局方案不同.由表7可看出,模型HD在不同情景下对应的最优枢纽布局方案存在差异.

综上所述:需求不确定情况下,不同的p值对布局方案影响不同,当p大于模型HS所有情景中的最大相对后悔值时,模型HR与模型HS求得的布局方案一致,而p小于该值时布局方案差异较大;需求确定情况下,不同需求对应的枢纽布局分配方案不同.

如表7所示,各情景下模型non-HD(指不分层的确定性需求下的布局方法,即重复利用中位模型分别对各级枢纽进行布局)的目标函数值远远大于分层布局(HD,HS,HR)的方法,即分层布局方法求解结果在可达性方面更具优势.另外,对于模型HR,当p=0.12时,情景4的相对后悔值比模型HS大,其他情景相对后悔值与模型HS相同;当p=0.05时,除情景3的相对后悔值比模型HS大,其他情景相对后悔值比HS小得多.可见,当p<0.12时模型HR的鲁棒性比模型HS更强.

表6 模型HS和HR求解结果比较

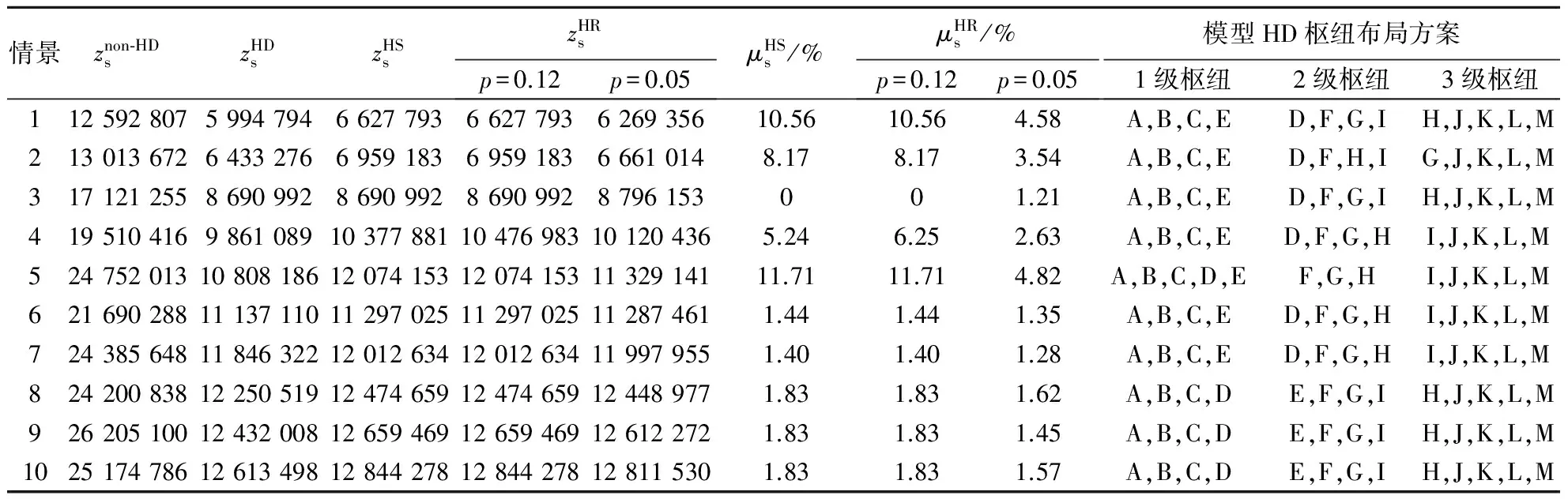
表7 各情景下不同模型相对后悔值的比较及模型HD的布局方案

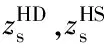
4.2.3 灵敏度分析

表8为覆盖范围或情景概率改变时,p取不同值时的目标函数值和枢纽布局方案(初始参数设置下的目标函数值和枢纽布局方案见表6).当各级枢纽覆盖范围从600,300,100 km变为500,300,100 km,p取不同值时,枢纽布局方案均没有变化，而分配方案变化,目标函数值变小.可见,覆盖范围对枢纽布局和分配方案有一定影响.若前5种情景的概率均增加0.05，而后5种情景概率均减少0.05,当p=0.15或0.12时,枢纽布局和分配方案不变,目标函数值变小,因为前5种情景对应的需求加权距离均比后5种小;当p=0.10或0.05时,枢纽布局方案和目标函数值均发生变化.可见,情景概率对枢纽布局方案有重要的影响.

表8 不同p值下覆盖范围变化、情景概率变化后模型HR的求解结果

5 结论

1) 针对城镇化进程中国家层面综合客运枢纽布局优化问题，构建了分层布局鲁棒优化模型.基于有能力限制的层级选址模型能反映枢纽等级系统的特征,同时结合鲁棒优化方法处理城镇化发展中需求的不确定性,模型更贴近实际情况.

2) 设计免疫克隆算法对模型求解,通过算例分析验证了算法的有效性.与软件CPLEX相比,算法在一定范围的p值下更高效.

3) 算例结果表明,分层布局方法优于重复使用中位模型分别对各级枢纽布局的方法,当p取值小于模型HS所有情景中的最大相对后悔值时,模型HR的求解结果比模型HS的求解结果具有更强的鲁棒性,同时p的取值、覆盖范围和情景概率对枢纽布局方案有重要影响.

4) 本文对城镇化快速发展背景下的国家层面综合客运枢纽布局规划有一定的理论参考意义.规划部门应充分分析枢纽等级系统的运行机理,考虑城镇化进程中各类不确定性因素,根据需求制定具有一定鲁棒性的布局方案,为省级层面综合客运枢纽布局规划提供正确指导.

References)

[1]Farahani R Z, Hekmatfar M, Fahimnia B, et al. Hierarchical facility location problem: models, classifications, techniques, and applications [J].Computers&IndustrialEngineering, 2014, 68: 104-117.

[2]Pehlivan C, Augusto V, Xie Xiaolan. Dynamic capacity planning and location of hierarchical service networks under service level constraints [J].IEEETransactionsonAutomationScienceandEngineering, 2014, 11(3): 863-880.

[3]Smith H K, Harper P R, Potts C N. Bicriteria efficiency/equity hierarchical location models for public service application [J].JournaloftheOperationalResearchSociety, 2013, 64(4): 500-512.

[4]Chen Zhifen, Chen Xiang, Li Qiang, et al. The temporal hierarchy of shelters: a hierarchical location model for earthquake-shelter planning [J].InternationalJournalofGeographicalInformationScience, 2013, 27(8): 1612-1630.

[5]Mestre A M, Oliveira M D, Barbosa-Povoa A. Organizing hospitals into networks: a hierarchical and multiservice model to define location, supply and referrals in planned hospital systems [J].ORSpectrum, 2012, 34(2): 319-348.

[6]Yan Yan, Zhang Baoxian, Zheng Jun, et al. Hierarchical location service for wireless sensor networks with mobile sinks [J].WirelessCommunicationsandMobileComputing, 2010, 10(7): 899-911.

[7]Shavandi H, Mahlooji H. Fuzzy hierarchical queuing models for the location set covering problem in congested systems [J].ScientiaIranica, 2008, 15(3): 378-388.

[8]Wang Zhen, Du Donglei, Gabor A F, et al. An approximation algorithm for the k-level stochastic facility location problem [J].OperationsResearchLetters, 2010, 38(5): 386-389.

[9]孙小年, 石琼. 省级区域公路运输枢纽宏观布局研究 [J]. 交通标准化, 2007 (9): 32-36. Sun Xiaonian, Shi Qiong. Research on macroscopic layout of provincial areal highway transportation hinge [J].TransportStandardization, 2007(9): 32-36.(in Chinese)

[10]刘强, 陆化普, 王庆云. 区域综合交通枢纽布局双层规划模型 [J]. 东南大学学报:自然科学版, 2010, 40(6): 1358-1363. Liu Qiang, Lu Huapu, Wang Qingyun. Bi-level programming model for regional integrated transportation hub layout [J].JournalofSoutheastUniversity:NaturalScienceEdition, 2010, 40(6): 1358-1363. (in Chinese)

[11]丁金学, 金凤君, 王成金, 等. 中国交通枢纽空间布局的评价、优化与模拟 [J]. 地理学报, 2011, 66(4): 504-514. Ding Jinxue, Jin Fengjun, Wang Chengjin, et al. Evaluation, optimization and simulation of the spatial layout of transport hubs in China [J].ActaGeographicaSinica, 2011, 66(4): 504-514. (in Chinese)

[12]李代坤, 何世伟, 申永生, 等. 基于免疫克隆算法的综合交通枢纽布局优化研究 [J]. 武汉理工大学学报:交通科学与工程版, 2012, 36(2): 382-386. Li Daikun, He Shiwei, Shen Yongsheng, et al. Layout optimization of comprehensive transportation hub based on immune clone algorithm [J].JournalofWuhanUniversityofTechnology:TransportationScience&Engineering, 2012, 36(2): 382-386. (in Chinese)

[13]Snyder L V, Daskin M S. Stochastic p-robust location problems [J].IIETransactions, 2006, 38(11): 971-985.

[14]黄友锐. 智能优化算法及其应用 [M]. 北京：国防工业出版社, 2008: 68-70.

Hierarchical layout robust optimization model for integrated passenger hub at national level

Li Tingting1Song Rui2

(1MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University, Beijing 100044,China) (2School of Traffic and Transportation,Beijing Jiaotong University, Beijing 100044, China)

In order to improve the efficiency of integrated passenger hub at national level, the relationship between integrated passenger hub classification and passenger transport demand is analyzed. The uncertainty of the passenger transport demand in the process of urbanization is taken into account. A model based on capacitated hierarchical location model and stochasticp-robust (pis relative regret restricted coefficient) optimization is proposed. An immune clonal algorithm is designed to solve the problem and a numerical example is given to validate the effectiveness of the model and algorithm. The results show that hierarchical layout model is superior to non-hierarchical layout model. Whenpis less than the maximum relative regret of hierarchical stochastic (HS) model, the result of hierarchical robust (HR) model has stronger robustness than that of the HS model and the immune clonal algorithm performs more efficiently than optimization software CPLEX. The value ofp, the coverage of hubs and the scenario probability greatly affect the layout planning scheme. The HR model provides decision references for integrated passenger hub layout planning.

transportation system engineering; layout optimization; hierarchical location model; integrated passenger hub; robust optimization; immune clonal algorithm

2014-08-04. 作者简介: 李婷婷(1985—),女,博士生;宋瑞(联系人),女,博士,教授,博士生导师,rsong@bjtu.edu.cn.

国家重点基础研究发展计划(973计划)资助项目(2012CB725403).

李婷婷,宋瑞.国家层面综合客运枢纽分层布局鲁棒优化模型[J].东南大学学报:自然科学版,2015,45(1):189-195.

10.3969/j.issn.1001-0505.2015.01.033

U491

A

1001-0505(2015)01-0189-07