曲线上货物列车超速引起的脱轨过程分析

龚 凯 向 俊 余翠英 毛建红,2

(1中南大学土木工程学院, 长沙 410075)(2华东交通大学土木建筑学院, 南昌 330013)

曲线上货物列车超速引起的脱轨过程分析

龚 凯1向 俊1余翠英1毛建红1,2

(1中南大学土木工程学院, 长沙 410075)(2华东交通大学土木建筑学院, 南昌 330013)

针对货物列车在曲线上因超速引起的脱轨问题,根据列车-轨道系统空间振动计算模型及列车脱轨能量随机分析理论,采用轮轨位移衔接条件并考虑轮轨“游间”的影响,提出了货物列车超速条件下的脱轨过程计算方法．根据该方法,对不同曲线轨道形位等工况下的货物列车脱轨过程进行了计算,分析了列车脱轨过程中的轮轨接触状态、轮轨相对位置及几何尺寸．研究结果表明，随着曲线半径的增大,在列车脱轨瞬间,转向架摇头角及转向架与钢轨横向相对位移逐渐减小,最大值分别为5.82°和78.1 mm.该结果可为研发机械式的列车脱轨检测装置提供理论依据和基础数据,进而确保该检测装置能在列车脱轨掉道的第一时间检测到位,及时停车．

铁路轨道;列车超速;脱轨力学机理;能量随机分析理论

近年来,随着铁路高速化和重载化的迅猛发展,列车轴重日益增大,编组辆数不断增加,行车速度也在逐渐提高,安全问题已成为头等大问题,而影响列车安全性的最大隐患是列车脱轨．引起列车脱轨的原因很多,可分为不明原因的脱轨和原因明确的脱轨2种．对于不明原因引起的列车脱轨,文献[1-6]通过深入研究取得了实质性研究成果.而原因明确的脱轨,如列车紧急制动、列车超速、无缝线路胀轨跑道、地震、大风及山体滑坡等引起的脱轨,近年来国内外时有发生[7-11],其中列车在曲线上超速引起的脱轨事故详见文献[11]．对于这类列车脱轨事故,希望在列车脱轨的第一时间能通知司机,从而及时停车．但在实际运营中,列车脱轨后,驾驶员通常不能及时发现,仍然前行,导致事故扩大化．为了减少损失,研发列车脱轨检测装置十分必要．

列车脱轨检测装置研发的关键在于如何准确地判定列车是否脱轨．然而,处理这一关键问题需要对列车脱轨过程及脱轨机理进行研究,以及分析列车脱轨时的轮轨相对位置和尺寸关系．但是,由于受到各种实际条件的限制,有限次行车脱轨试验难以做出列车脱轨,必须进行多次试验才有可能做出列车脱轨,而这样做是不现实的．因此对列车脱轨过程进行理论计算不失为一种好的方法．目前,肖新标等[12-14]针对轨道结构失效、轨道鼓胀、强风及地震条件下的高速列车脱轨机理进行了研究，而关于列车在超速条件下的列车脱轨机理及列车脱轨过程研究迄今为止国内外鲜见报道．

为此,本文以列车-轨道系统(以下称为“此系统”)空间振动计算模型及列车脱轨能量随机分析理论为基础,提出列车超速条件下的脱轨过程计算方法;采用该方法对货物列车脱轨过程进行计算,并对列车脱轨过程中及脱轨瞬间的轮轨接触状态、相对位置及尺寸关系等进行分析,揭示该条件下列车的脱轨规律,为进一步研发机械式的列车脱轨检测装置提供理论依据和基础数据．

1 列车超速条件下脱轨过程计算方法

采用能量原理的思想,将列车和轨道视为一个整体系统．机车车辆均离散为具有26个自由度的多刚体计算模型,其中,车体及转向架均考虑伸缩、横摆、浮沉、侧滚、点头及摇头共6个自由度,每个轮对仅考虑浮沉及横摆2个自由度．同时,针对轨道结构的特点,将其离散为n个轨段单元集合,每个轨段单元均考虑为具有34个自由度计算模型．当列车在时刻t时,有m辆车运行在长度为L的轨道结构上,则第i辆车的空间振动势能为ΠVi,经叠加可得列车空间振动总势能[15]为

(1)

在长度为L的轨道结构中,第j个轨段单元的空间振动势能为ΠTj,经过叠加n个轨段单元空间振动势能,即可推导出轨道结构空间振动总势能[15]为

(2)

要将列车系统振动方程和轨道系统振动方程联系起来必须考虑轮轨衔接条件.轮轨衔接条件分为轮轨相互作用力衔接条件和轮轨位移衔接条件．采用轮轨相互作用力衔接条件,可通过迭代法求解,但是考虑到轮轨“游间”的影响,无法表达车轮与钢轨之间的横向作用力衔接条件,使得迭代法求出的解不具有唯一性,得出的横向振动响应也不是此系统实际的横向振动响应．为了解决这一难题,本文采用列车脱轨能量随机分析理论中提出的轮轨位移衔接条件,即轮轨横向相对位移=车轮横向位移-钢轨横向位移-轨道横向几何不平顺，轮轨竖向相对位移=车轮竖向位移-钢轨竖向位移-轨道竖向几何不平顺，并考虑了轮轨“游间”的影响，则在时刻t,此系统空间振动总势能为

Π=ΠV+ΠT

(3)

按照上述轮轨位移衔接条件,根据弹性系统动力学总势能不变值原理[16]及形成系统矩阵的“对号入座”法则[17],建立此系统空间振动矩阵方程,即

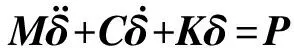
(4)

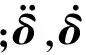
荷载列阵P主要由列车自重和轨道几何不平顺组成,经计算只能解出此系统由列车自重及轨道不平顺引起的竖向振动响应,而无法求出此系统的横向振动响应．为此,文献[16]指出车辆构架实测蛇形波或车辆构架人工蛇形波分别可作为此系统横向振动随机分析和确定性分析的激振源,并将构架蛇形波标准差σp作为此系统横向振动的输入能量．这样,可将车辆构架蛇形波、列车自重及轨道几何不平顺同时代入式(4)中,此时,在此系统空间振动矩阵方程中分别有s个已知位移δs和w个未知速度δw.将式(4)中的矩阵进行分块,可得

(5)

将式(5)展开,可得

(6)

(7)

式(6)右边各项均已知,经计算可得出此系统空间振动响应;式(7)为非独立方程．在计算中,采用Wilson-θ法对式(6)进行求解,时间步长设为0.01 s,θ为1.4．同时,以Fortran PowerStation 4.0平台为基础,编制了相应的计算程序．

构架蛇形波标准差σp可作为此系统横向振动的输入能量,构架实测(人工)蛇形波可以作为此系统横向振动随机分析的激振源．为了进一步分析此系统的横向振动,课题组在多条铁路干线上实测大量各时速下货物列车的构架蛇形波,并采用工程概率法得到了各车速下具有99%概率的标准差σp,绘制了车速V与标准差σp的关系曲线(σp-V)．根据该曲线可以查出对应车速下的标准差σp,进而采用Monte-Carlo法随机模拟出一条构架人工蛇形波,将其输入此系统,即可求出相应的空间振动响应．但是,上述标准差σp是在列车正常运行情况下通过实测和统计得到的,而列车脱轨时的实际构架蛇形波是无法测出的,相应的标准差也难以统计．但从系统能量的思想出发,根据能量守恒原理,此系统输入能量越大,其振动响应越大,反之则越小.振动响应是在此系统自身约束边界范围内产生的.例如:一根受到外力压缩的弹簧系统,当该弹簧系统没有约束边界且只在弹簧一端施加外力时,其振动响应无法产生,外力对其不产生作用,外力产生的能量也未输入弹簧系统;而如果将弹簧的一端固定,另一端施加外力,随着外力的持续作用,弹簧将被压缩一定距离.此时,外力产生的能量输入弹簧系统,当外力产生的能量大于弹簧系统本身能够抵抗的能量时,弹簧系统失稳,表现为弹簧被压断,而这个弹簧系统本身能够抵抗的最大输入能量即为弹簧系统本身的极限抗力所做的功．根据这一思想,可通过计算得出列车脱轨时的实际构架蛇形波标准差．在此系统中,其空间振动响应是有轮轨相互作用引起的,轮轨之间之所以能够产生相互作用是因为轮轨之间的相互约束影响.相对车轮而言,2根钢轨就是车轮的约束边界,当车轮的运动超出了钢轨约束边界时,列车就发生了脱轨．而此系统横向振动输入能量采用构架蛇形波标准差来表示,那么,当输入能量足以使得车轮处于钢轨约束边界的临界状态时,其相应的输入能量即为此系统本身能够抵抗的最大能量,即此系统的极限抗力做功(用σc表示).σc就是列车脱轨时的实际构架蛇形波标准差．为此,按照车轮脱轨几何准则,采用试算法,可以算得列车脱轨时的实际构架蛇形波标准差σc．具体过程见文献[5]．

基于车轮脱轨几何准则及试算法,可以实现列车超速引起的脱轨计算．列车超速即为列车行车速度超过轨道线路要求的最高速度,从而致使列车发生脱轨,列车超速引起的脱轨事故大多发生在曲线线路上．根据文献[18]中的曲线轨道上超高限速计算方法,可以得出曲线轨道超高限速Vmax, 其计算式为

(8)

式中,hQY为未被平衡的容许欠超高,一般取75 mm[18];R为曲线半径;h为曲线外轨实设超高．

由式(8)可以看出,曲线半径R、曲线外轨实设超高h与超高限速Vmax成正比例关系,是影响Vmax大小的关键因素．因此,本文中的计算工况主要通过变化曲线轨道的几何形位进行设置．

在实现列车脱轨过程计算中,首先将曲线轨道超高限速Vmax作为列车运行速度的下限,然后,根据σp-V曲线,查出相应车速的构架蛇形波标准差σp,随机模拟出一条构架人工蛇形波,并以此作为此系统的横向振动激振源，计算每一时间步长下的车轮悬浮量,检查悬浮量是否达到车轮脱轨几何准则中要求的数值(25 mm),若未达到,继续下一步计算,直至计算完成;若仍未达到,则假定更大的列车行车速度,重复上述过程,直至车轮悬浮量达到车轮脱轨几何准则为止．此时,钢轨横向约束失效,车轮轮缘爬至钢轨顶面中点,列车超速引起的脱轨过程计算完毕.此系统各部件相应的振动响应即为列车脱轨时的振动响应,计算采用的构架蛇形波标准差σp即为列车超速条件下脱轨时的实际构架蛇形波标准差σc．

2 计算实例与分析

鉴于我国铁路自提速以来空载货车脱轨事故率相对较大[19]，计算中采用的列车编组为1辆DF4型机车+12辆C62型空载货车．曲线轨道结构为:60 kg/m型钢轨，混凝土轨枕，轨枕间距为0.543 5 m，普通碎石道砟,曲线轨道几何形位参数如表1所示．

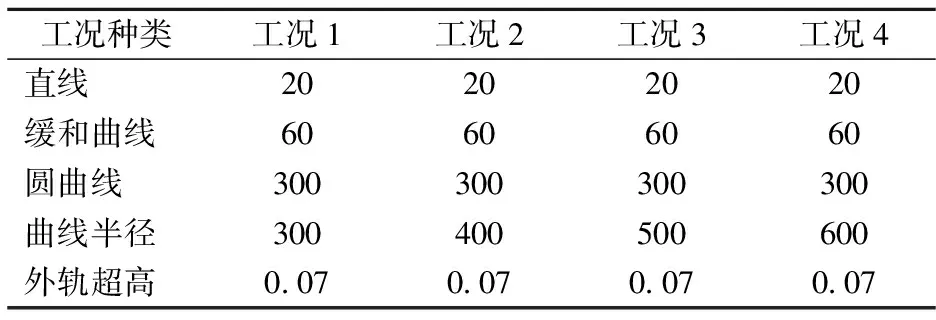
表1 曲线轨道几何形位参数 m

将表1中的曲线半径和外轨超高代入式(8)中,可求出各工况下的超高限速Vmax,以该速度作为列车行车速度的下限,并在σp-V曲线中查找相应速度下的构架蛇形波标准差σp,随机模拟出一条构架蛇形波作为此系统的横向振动激振源．同时,此系统竖向振动激振源采用轨道几何不平顺．按照前述计算方法,计算各工况下列车超速引起的脱轨过程,计算结果如表2所示.

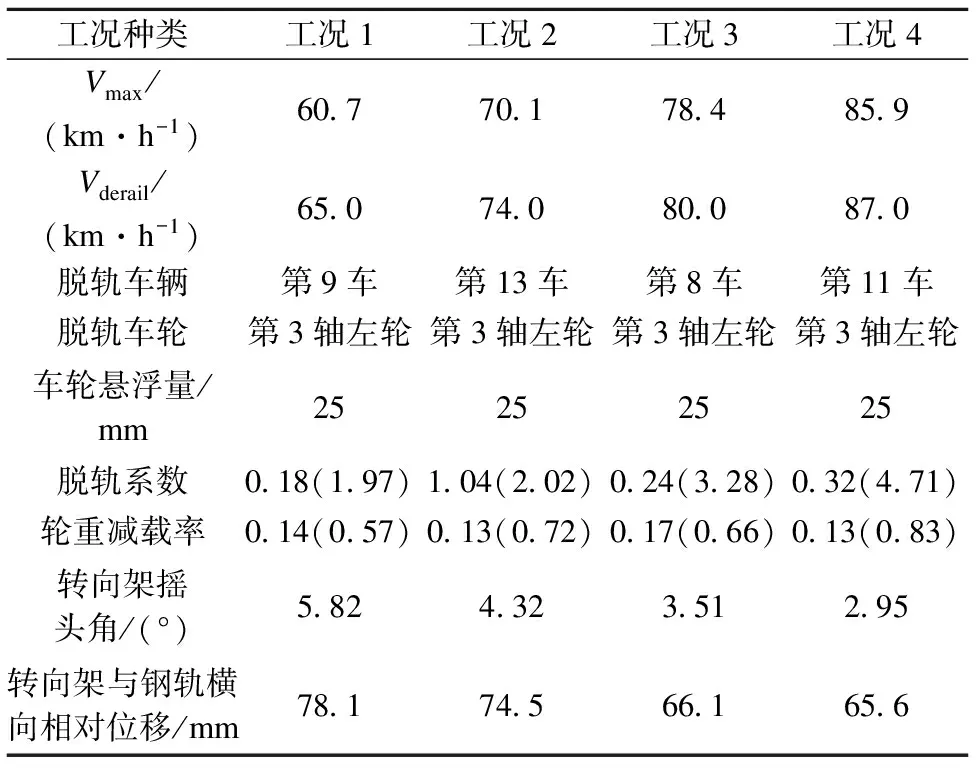
表2 列车超速引起的脱轨过程计算结果

表2中,Vderail为列车脱轨时的行车速度;各车轴左轮运行在曲线外侧轨道上,右轮运行在曲线内侧轨道上;脱轨系数和轮重减载率括号外为列车车轮脱轨瞬间对应的数值,括号内为列车车轮脱轨过程中的最大值.

表2表明,列车发生脱轨时均是左侧车轮脱轨掉道,即曲线轨道外侧钢轨对应的车轮发生了脱轨,这可能与曲线未被平衡的超高有关;同时,各工况在列车脱轨瞬间的车轮悬浮量均达到了车轮脱轨几何准则要求的数值．工况1对应车轮悬浮量时程如图1所示．

由表2还可以看出,在列车脱轨过程中,各工况脱轨系数最大值分别为1.97,2.02,3.28和4.71,均超过了GB/T 5599—85[20]中脱轨系数要求的限值,其中最大值几乎达到了规范限值的4倍,但是列车并没有发生脱轨;而在列车脱轨瞬间,列车脱轨系数均小于限值要求,其中大部分脱规系数与规范限值相差较远,此时列车发生了脱轨．图2为工况1脱轨系数时程曲线．

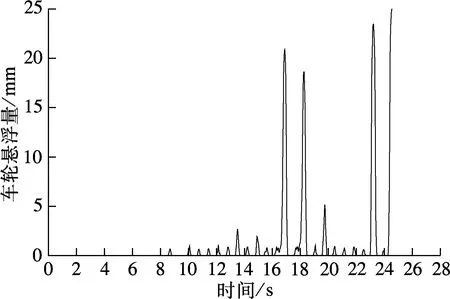
图1 第9车第3轴左侧车轮悬浮量时程(工况1)

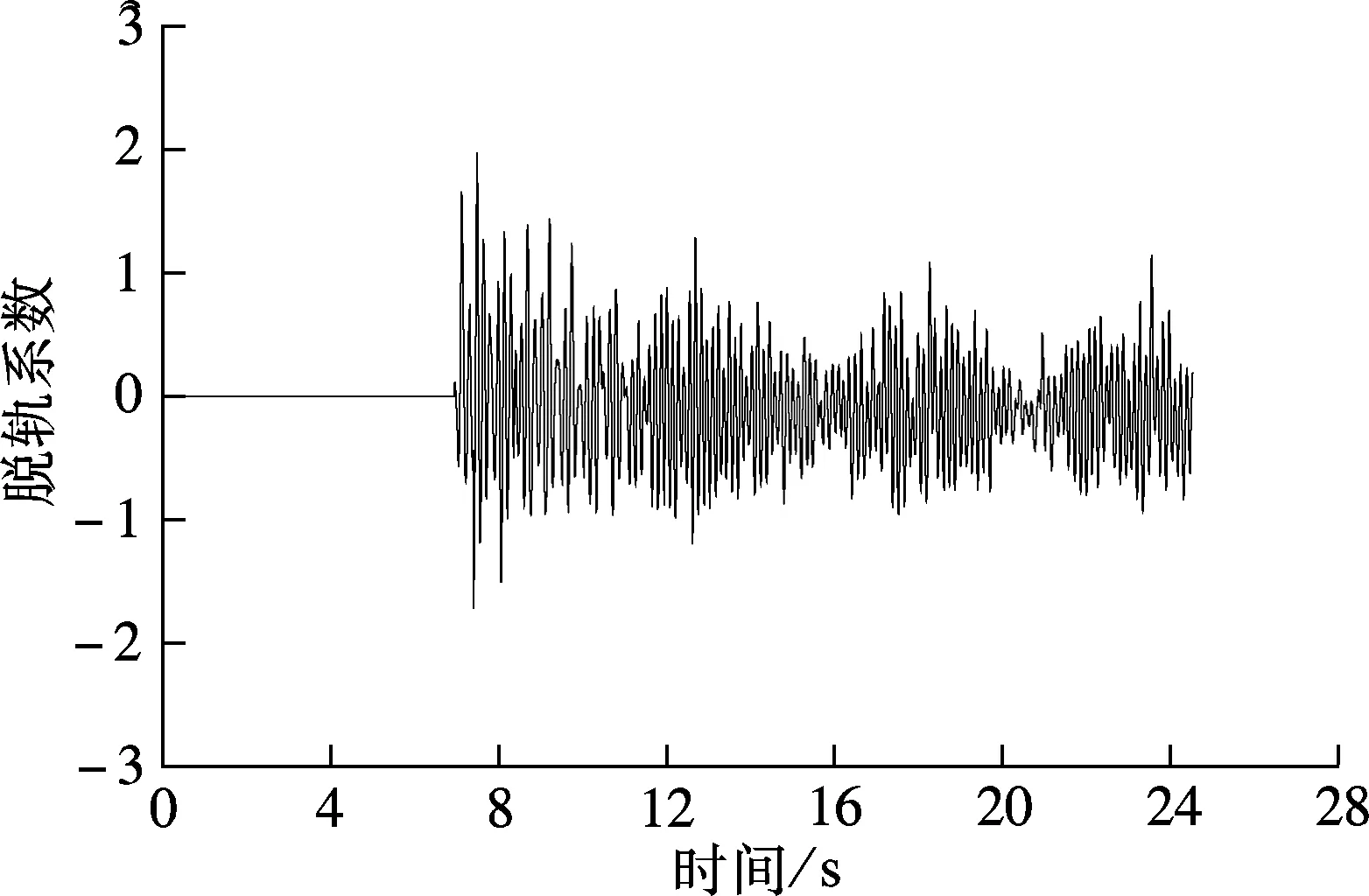
图2 第9车第3轴左侧车轮脱轨系数时程(工况1)

轮重减载率是评判列车运行是否安全的重要指标,但至今还未能通过实测得到轮重减载率,特别是列车脱轨瞬间的轮重减载率实测值.同时,理论计算的列车脱轨瞬间轮重减载率也较少．从表2可以看出,在列车脱轨瞬间,各工况轮重减载率计算值均较小,车轮未出现严重减载,但是列车发生了脱轨;而在列车脱轨过程中,轮重减载率最大值有的没有超过规范限值要求,有的超过了,其中超过规范限值的最大值高达0.83,车轮出现严重减载,但列车仍未发生脱轨．图3为工况1中的轮重减载率时程曲线．

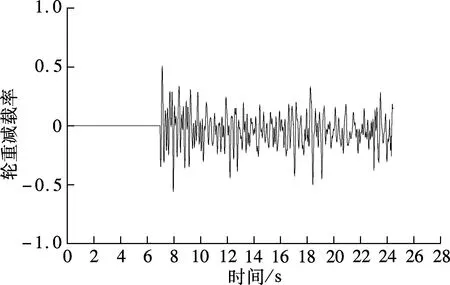
图3 第9车第3轴左侧车轮轮重减载率时程(工况1)

最后,通过对比表2中转向架摇头角、转向架与钢轨横向相对位移可知,随着曲线半径的增大,其数值逐渐减小．由此说明,曲线半径对列车脱轨时转向架的相对位置有一定的影响,并且半径越小,转向架横向振动越剧烈,振动响应越大．为更加直观地理解整个脱轨过程中转向架摇头角、转向架与钢轨横向相对位移的时程变化,图4和图5给出了与工况1相应指标的时程曲线．

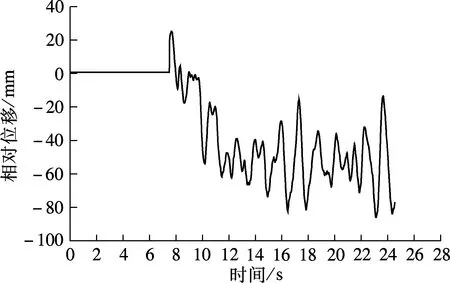
图5 第9车转向架与钢轨横向相对位移(工况1)

3 结论

1) 基于列车-轨道系统空间振动计算模型及列车脱轨能量随机分析理论,采用轮轨位移衔接条件并考虑轮轨“游间”的影响,提出了超速条件下列车脱轨过程计算方法;根据此法,按照弹性系统动力学总势能不变值原理及形成系统矩阵的“对号入座”法则,建立了此系统空间振动矩阵方程,采用Wilson-θ法对矩阵方程进行了求解,并编制了相应的计算程序,对货物列车超速脱轨过程进行了计算,并对计算结果进行了分析．

2) 脱轨系数和轮重减载率是评定列车运行是否安全的重要指标,但从对列车脱轨过程分析中可知,在列车脱轨瞬间,脱轨系数不一定超过规范限值,如工况1中第9车第3轴左侧车轮脱轨系数为0.18；而在脱轨过程中,脱轨系数最大值有的则远大于限值要求，如工况4中第11车第3轴左侧车轮脱轨系数为4.71,几乎达到规范限值的4倍,但列车此时没有发生脱轨．同时,在列车脱轨瞬间,轮重减载率均小于限值要求,列车发生了脱轨;而在列车脱轨过程中,工况4中的轮重减载率最大值高达0.83,车轮出现严重减载,列车却未出现脱轨．

3) 列车脱轨瞬间转向架摇头角、转向架与钢轨横向位移随着曲线轨道半径的增大逐渐减小,在曲线轨道半径为300 m的小半径曲线轨道上转向架摇头角及转向架与钢轨横向相对位移最大,分别为5.82°和78.1 mm．由此说明,计算小半径曲线轨道上的列车脱轨全过程有助于寻找转向架摇头角、转向架与钢轨横向位移的最大值,这些结果可为研发机械式列车脱轨检测装置提供基础数据,并为进一步增强该装置的通用性提供理论依据．而研发该装置的目的是为了确保其能在列车脱轨的第一时间检测到位,使列车及时停车,避免二次脱轨事故的发生,将损失降到最低．

References)

[1]向俊,曾庆元. 直线货物列车脱轨过程计算[J]. 铁道学报,2002, 24(2):104-108. Xiang Jun, Zeng Qingyuan. Simulation of the derailment courses of freight train on tangent track[J].JournaloftheChinaRailwaySociety, 2002, 24(2): 104-108. (in Chinese)

[2]向俊,赫丹,左一舟,等. 京山线滦河老桥上货物列车脱轨分析[J]. 交通运输工程学报,2004, 4(3):16-19. Xiang Jun, He Dan, Zuo Yizhou, et al. Derailment analysis of freight train on old Luanhe bridge on Jingshan line in China[J].JournalofTrafficandTransportationEngineering, 2004, 4(3): 16-19. (in Chinese)

[3]向俊,杨军祥,赫丹,等. 焦柳线酉水大桥上货物列车脱轨分析[J]. 中南大学学报, 2006, 37(1):169-175. Xiang Jun, Yang Junxiang, He Dan, et al. Derailment analysis of freight train on Youshui Bridge on Jiaoliu line[J].JournalofCentralSouthUniversity, 2006, 37(1): 169-175. (in Chinese)

[4]向俊,周志辉,曾庆元. 列车脱轨研究最新进展[J]. 铁道科学与工程学报,2005, 2(5):1-8. Xiang Jun, Zhou Zhihui, Zeng Qingyuan. Recent developments in train derailment research[J].JournalofRailwayScienceandEngineering, 2005, 2(5): 1-8. (in Chinese)

[5]曾庆元,向俊,周志辉,等. 列车脱轨分析理论与应用[M]. 长沙:中南大学出版社, 2006: 204-276.

[6]向俊,曾庆元. 铁路钢板梁桥上货物列车脱轨全过程仿真[J]. 铁道科学与工程学报,2007, 4(3):1-4. Xiang Jun, Zeng Qingyuan. Simulation of entire derailment courses of freight trains on railway steel plate beam bridges[J].JournalofRailwayScienceandEngineering, 2007, 4(3): 1-4. (in Chinese)

[7]陈良军，周文峰. 广州往重庆脱轨事故[J]. 广东交通,2008(4):37. Chen Liangjun, Zhou Wenfeng. The derailment accident from Guangzhou to Chongqin[J].GuangdonTraffic, 2008(4): 37. (in Chinese)

[8]Gawthrope R G. Wind effects on ground transportation[J].JournalofWindEngineeringandIndustrialAerodynamics, 1994, 52(1): 73-92.

[9]Earthquake Engineering Research Institute. Special earthquake report-preliminary observation on the Niigata Ken Chuetsu[R]. Japan: Kyoto University, 2005.

[10]Brabie D. On the influence of rail vehicle parameters on the derailment process and its consequence[EB/OL]. (2005)[2014-07]. http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A8040&dswid=7024.

[11]杨骏. 西班牙列车何以“死亡狂奔”[N]. 新华每日电讯,2013-7-26(3).

[12]肖新标. 复杂环境状态下高速列车脱轨机理研究[D]. 成都:西南交通大学交通运输工程学院,2013.

[13]Deng Yongquan, Xiao Xinbiao. Effect of cross-wind on high-speed vehicle dynamic derailment[C]//Proceedingsofthe8thInternationalConferenceofChineseLogisticsandTransportationProfessionals-Logistics:theEmergingFrontiersofTransportationandDevelopmentinChina. Chengdu, China, 2008: 2287-2293.

[14]Xiao Xinbiao, Ling Liang, Jin Xuesong. A study of the derailment mechanism of a high speed train due to an earthquake[J].VehicleSystemDynamic, 2012, 50(3): 449-470.

[15]李德建. 列车-轨道时变系统空间振动分析[D]. 长沙:长沙铁道学院土木建筑学院,1996.

[16]曾庆元,郭向荣. 列车桥梁时变系统振动分析理论与应用[M]. 北京: 中国铁道出版社, 1999: 21-29.

[17]曾庆元,杨平. 形成系统矩阵的“对号入座”法则与桁梁空间分析的桁段有限元法[J]. 铁道学报, 1986, 8(2):48-59. Zeng Qingyuan, Yang Ping. The “set-in-right-position” rule for forming structural matrices and the finite truss element method for space analysis of truss bridge[J].JournaloftheChinaRailwaySociety, 1986, 8(2): 48-59. (in Chinese)

[18]陈秀方. 轨道工程[M]. 北京:中国建筑工业出版社, 2004: 97-102.

[19]周世越, 任珠芳, 张辉. 货车直线区段脱轨机理与防范措施的探讨[J].上海铁道大学学报, 1999, 20(6): 38-42. Zhou Shiyue, Ren Zhufang, Zhang Hui. A discussion on the theory and precaution measurement of freight car derailment [J].JournalofShanghaiTiedaoUniversity, 1999, 20(6): 38-42. (in Chinese)

[20]中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会. GB/T 5599—1985铁道车辆动力学性能评定和试验鉴定规范[S]. 北京:中国铁道出版社,1985.

Analysis on freight train derailment course induced by overspeed in curve

Gong Kai1Xiang Jun1Yu Cuiying1Mao Jianhong1,2

(1School of Civil Engineering,Central South University,Changsha 410075,China) (2School of Civil Engineering and Architecture,East China Jiaotong University,Nanchang 330013,China)

For the freight train derailment problem in curve induced by overspeed, using the wheel-rail conjunction condition and considering the influence of clearance between wheel flange and gage line, the freight train derailment course calculation method is presented based on the spatial vibration calculation model of the train-track system and the energy random analysis theory of train derailment. According to this method, freight train derailment course is calculated under different curve track geometry conditions. Meanwhile, the contact status, the relative position and the geometric size of wheel-rail in the derailment course are also analyzed. Study results show that, at the moment when the train derailed, the bogie yaw angle and the lateral relative displacement between bogie and rail decreases with the increase of curve radius, the maximum values being 5.82° and 78.1 mm respectively. The results can provide theoretical basis and data for the development of mechanical train derailment detection device, and make it possible to detect the risk before derailment and stop the train timely.

railway track; train overspeed; mechanical mechanism of derailment; random energy analysis theory

2014-07-10. 作者简介: 龚凯(1986—), 男，博士生； 向俊(联系人), 男, 博士, 教授，博士生导师，jxiang@mail.csu.edu.cn.

国家自然科学基金委员会与神华集团有限公司联合资助项目(U1261113)、高等学校博士学科点专项科研基金资助项目(20100162110022)、牵引动力国家重点实验室开放课题资助项目(TPL0901,TPL1214).

龚凯,向俊,余翠英，等.曲线上货物列车超速引起的脱轨过程分析[J].东南大学学报:自然科学版,2015,45(1):172-177.

10.3969/j.issn.1001-0505.2015.01.030

U213.2

A

1001-0505(2015)01-0172-06