旋转弹仓的自适应模糊滑模控制
2015-05-06钱林方徐亚栋蒋清山杨会东
邹 权 钱林方 徐亚栋 蒋清山 杨会东
(1南京理工大学机械工程学院,南京210094)(2北方自动化技术研究所,太原030006)
旋转弹仓的自适应模糊滑模控制
邹 权1钱林方1徐亚栋1蒋清山1杨会东2
(1南京理工大学机械工程学院,南京210094)(2北方自动化技术研究所,太原030006)
针对存在啮合冲击、非线性摩擦以及参数大范围变化的旋转弹仓的位置控制问题,提出了一种自适应模糊滑模控制算法.该算法由2个模糊系统组成,分别用于逼近未知的理想控制律和补偿逼近误差,不需要知道系统的数学模型,具有较好的鲁棒性.在模糊逼近系统中,引入自适应算法在线调整模糊系统参数,改善了控制性能,提高了鲁棒性;在模糊补偿系统中,根据滑模变量调整控制作用,保证了滑模条件,削弱了抖振.空载、半载和满载3种情况下的实验结果表明,所提出的自适应模糊滑模控制算法对旋转弹仓的参数变化、啮合冲击以及非线性摩擦等不敏感,具有较高的控制精度.
模糊逻辑;滑模控制;自适应调整;旋转弹仓
旋转弹仓用于存储弹丸并把指定弹丸转送至弹仓取弹口,其定位精度对取弹可靠性有较大影响.旋转弹仓控制的难点在于:① 弹仓的转动惯量以及摩擦力矩随弹丸数量的变化而发生较大的变化,满载和空载时可相差数倍;② 即使在弹丸数量不变的情况下,弹仓的转动惯量也会随着其角位置的变化而变化[1];③ 弹仓的驱动链轮一般只有少数几个轮齿,弹仓在高速转动时链轮与弹链之间将会产生较大的啮合冲击作用;④ 弹仓采用开放式链传动结构,由环境引起的摩擦变化不可忽视.目前,旋转弹仓一般采用定常状态反馈控制算法,文献[1]提出了一种基于线性矩阵不等式的最优保性能控制算法,使用Matlab的LMI工具箱获得了定常最优状态反馈控制律;文献[2]利用满意控制理论给出了一种能够满足期望性能的控制器设计方法,通过极点配置使闭环系统具有满意的动态品质.当弹仓参数发生较大变化时,定常状态反馈的控制性能可能会下降.
滑模控制(sliding mode control, SMC)对参数变化以及外部扰动不敏感,广泛应用于高性能伺服系统[3-5].文献[6-8]采用模糊系统逼近未知的理想控制律,实现了一类机电伺服系统的无模型控制;文献[9]根据系统状态调整控制作用,在保证滑模条件的前提下,有效地削弱了抖振.文献[10]采用自适应策略调整模糊系统参数,简化了模糊系统的设计,提高了系统的鲁棒性.文献[11]采用自适应模糊系统逼近未知非线性函数,实现了一类不确定非线性系统的有限时间控制.文献[12]采用模糊系统逼近切换控制项,有效地削弱了抖振.
本文受文献[6,9]的启发,提出了一种新型的自适应模糊滑模控制方法,采用模糊逻辑逼近未知的理想控制律,不需要精确知道系统的数学模型;自适应调整模糊系统的参数,简化了控制器的设计,提高了系统的鲁棒性;根据滑模变量调整控制作用,在保证滑模条件的前提下,有效地削弱了抖振.空载、半载和满载3种情况下的实验结果表明,本文提出的自适应模糊滑模控制算法对系统参数变化以及外部扰动不敏感,具有较高的控制精度.
1 旋转弹仓的动力学方程
旋转弹仓由永磁同步电机通过减速装置驱动,电机的电气时间常数远远小于机械时间常数,因此可以忽略电流环动态.当永磁同步电机采用id=0的矢量控制技术时,旋转弹仓的动力学方程可以表示为
(1)
式中,J为等效转动惯量;B为等效黏性摩擦系数;Td为等效扰动之和,包括负载力矩、非线性摩擦、啮合冲击以及其他难以建模的动态;KT为电机转矩常数,不失一般性,KT> 0;θ为电机转子角位移;u为控制输入,即q轴电流.由式(1)化简可得
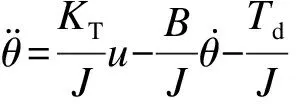
(2)
式中,Ap=KT/J,Bp=-B/J,Dp=-1/J.不失一般性,Ap> 0,Bp< 0,Dp< 0.
假定给定的运动轨迹θd及其一阶导数连续且有界,二阶导数有界,对于旋转弹仓位置控制系统式(2),设计有界的控制律u,使得旋转弹仓在参数发生变化和/或受到外部扰动时,其输出θ也能够跟踪θd,并且跟踪误差尽量小.
2 控制器设计
2.1 模糊逼近系统
定义位置跟踪误差
e=θd-θ
(3)
取如下的积分型滑模函数[13]:
(4)
式中,λ为待设计的滑模面参数,λ>0.λ决定了系统状态位于滑模面上时的控制性能,根据期望的控制性能选取λ值.
假设系统参数Ap,Bp和Dp精确已知,等效扰动Td是可测的或可预知的,考虑如下的理想控制率:
(5)
把理想控制律式(5)代入式(2),化简可得
(6)
由式(6)可知,当t→∞时,跟踪误差e→0,且其动态品质可由λ调整.然而在实际系统中,参数Ap,Bp和Dp是时变的或难以精确知道的,等效扰动Td是不可测且难以预知的,故理想控制律式(5)不可实现.根据模糊逼近理论[14-15],模糊系统能够以任意精度逼近任意连续函数,因此可以采用模糊系统逼近理想控制律式(5).
设计模糊系统逼近理想控制律式(5),取滑模函数s为模糊输入变量,模糊输出变量为u1,模糊变量的隶属度函数如图1所示,图中,s0为待定常数且s0> 0,αi(i=1,2,3)为可调参数.
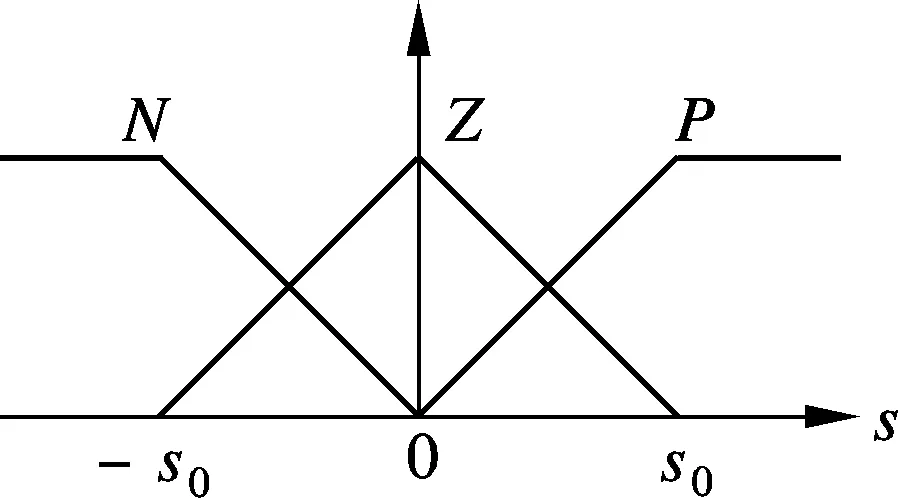
(a) s的隶属度函数
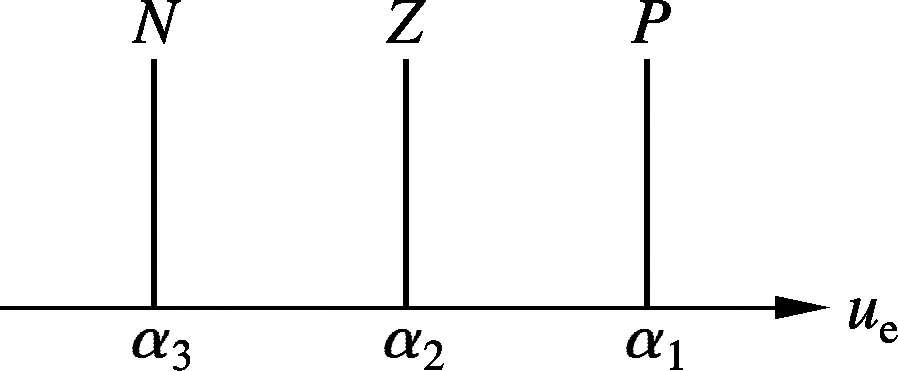
(b) u1的隶属度函数
假设模糊逼近系统的规则库由以下3条模糊规则组成.
R1: ifsisPthenu1isP.
R2: ifsisZthenu1isZ.
R3: ifsisNthenu1isN.
其中,P(正)、Z(零)、N(负)分别为相应模糊集合上的模糊子集.当采用乘机推理机、加权平均解模糊器时,模糊逼近系统的输出u1可表示为
(7)
式中,0≤wi≤1(i=1,2,3)为各模糊规则的加权系数,即模糊输入变量s在各模糊子集上的隶属度;αT=[α1,α2,α3]为可调参数向量;ξT=[ξ1,ξ2,ξ3]T,ξi定义为
(8)
(9)
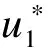

(10)
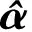
2.2 模糊补偿系统
在常规SMC中,为了保证滑模条件而引入的切换控制项会引起抖振,模糊逻辑与滑模控制相结合是削弱抖振的有效方法之一[9,12].为了削弱抖振,当系统误差状态接近滑模面时,应该减小控制作用以避免抖振;当系统误差状态远离滑模面时,应该增大控制作用以快速减小误差.根据上述原则,设计模糊补偿系统并引入以下3条模糊规则[9].
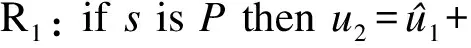
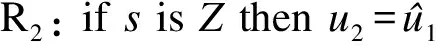
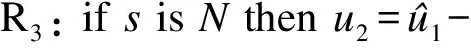
其中,u2为模糊补偿系统的输出;r为待设计的模糊系统参数,且r>0.滑模函数s为模糊系统输入,其隶属度函数如图2所示,图中s1为待定的常数,且s1>0.
模糊补偿系统中模糊输入s采用三角形隶属度函数,故对任意的模糊输入s有o1+o2+o3=1,其中,0≤oi≤1(i=1,2,3)为模糊规则Ri(i=1,2,3)的加权系数.当采用乘机推理机时,oi(i=1,2,3)即为模糊输入s在各模糊子集上的隶属度.采用加权平均解模糊器时,模糊输出u2可以表示为
(11)
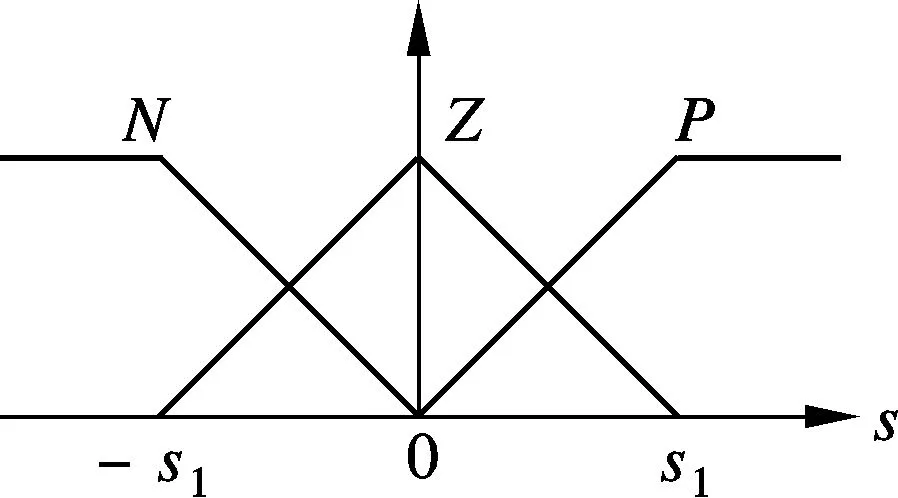
图2 模糊补偿系统中s的隶属度函数
由图2可知,在模糊补偿系统中,对于任意的模糊输入s,只有以下4种情况之一被满足:
①s≥s1,此时R1被触发,故o1=1,o2=o3=0,s(o1-o3)>0;
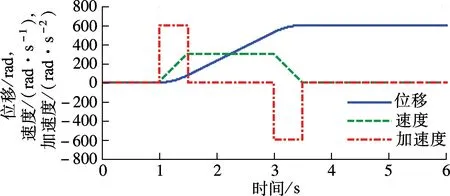
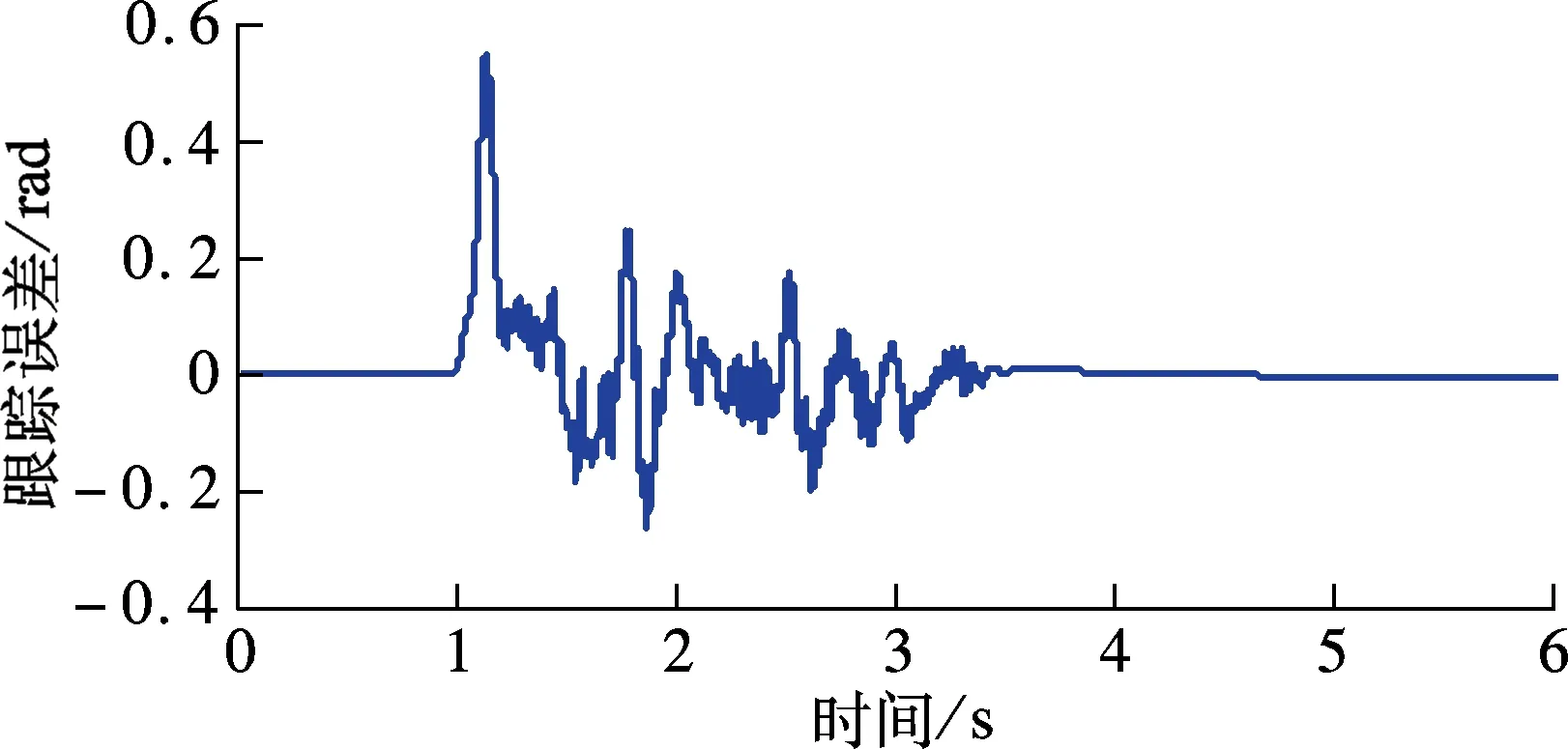
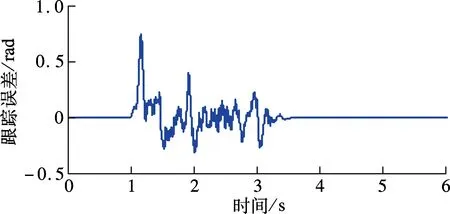
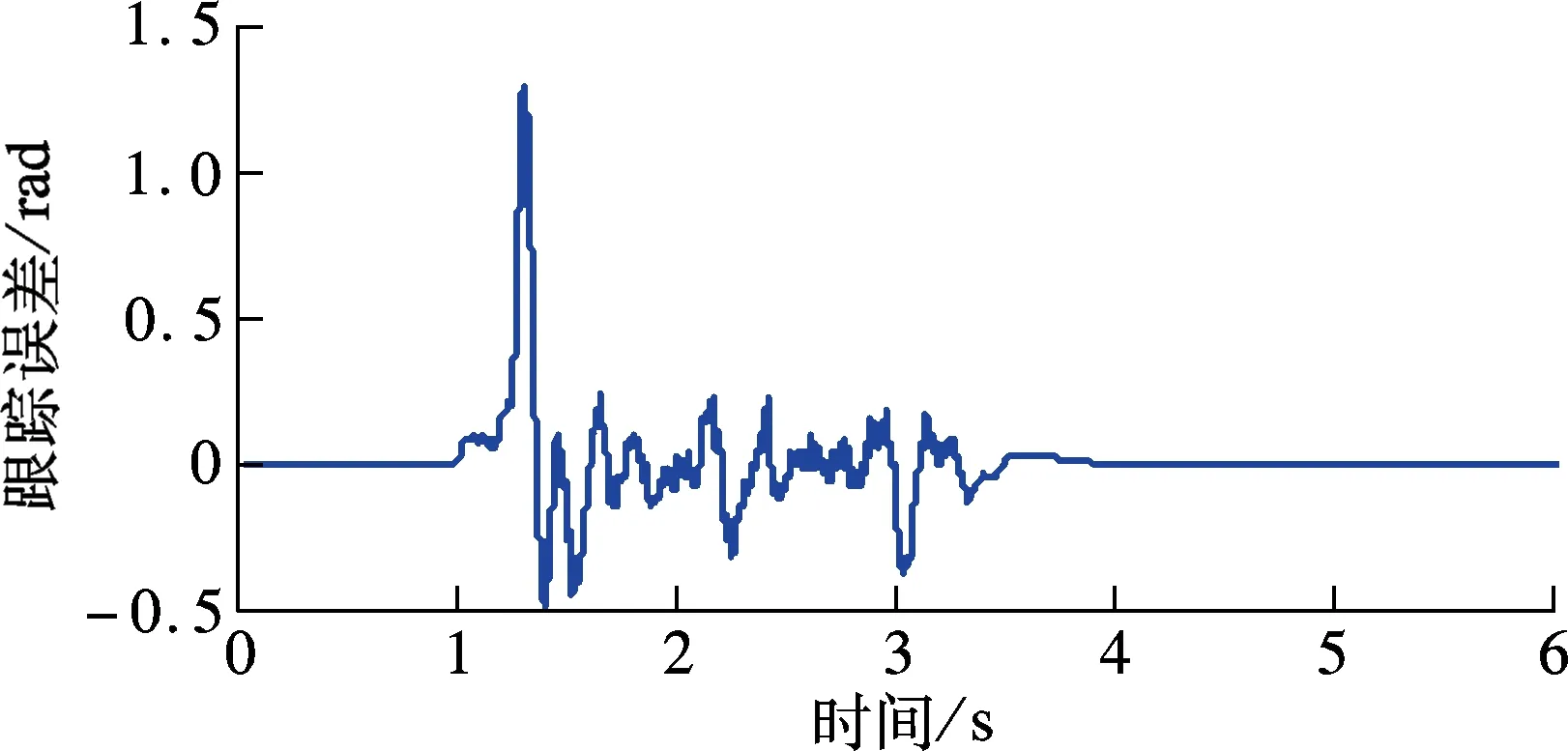
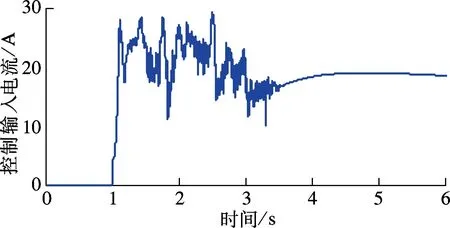
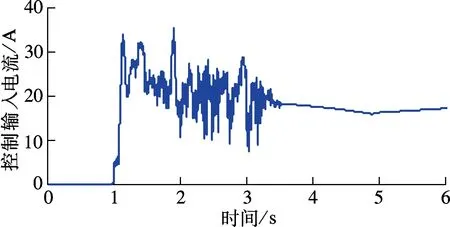
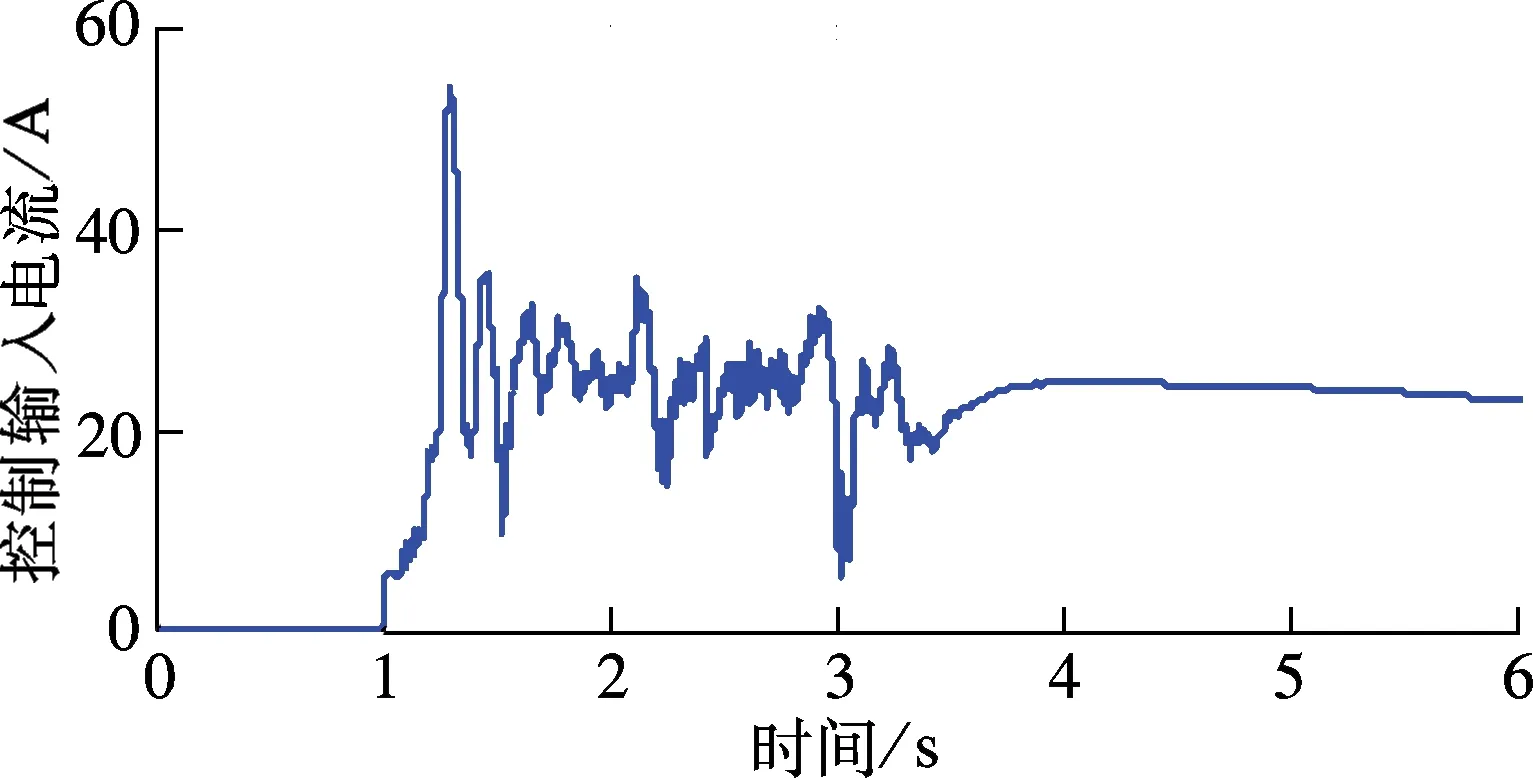
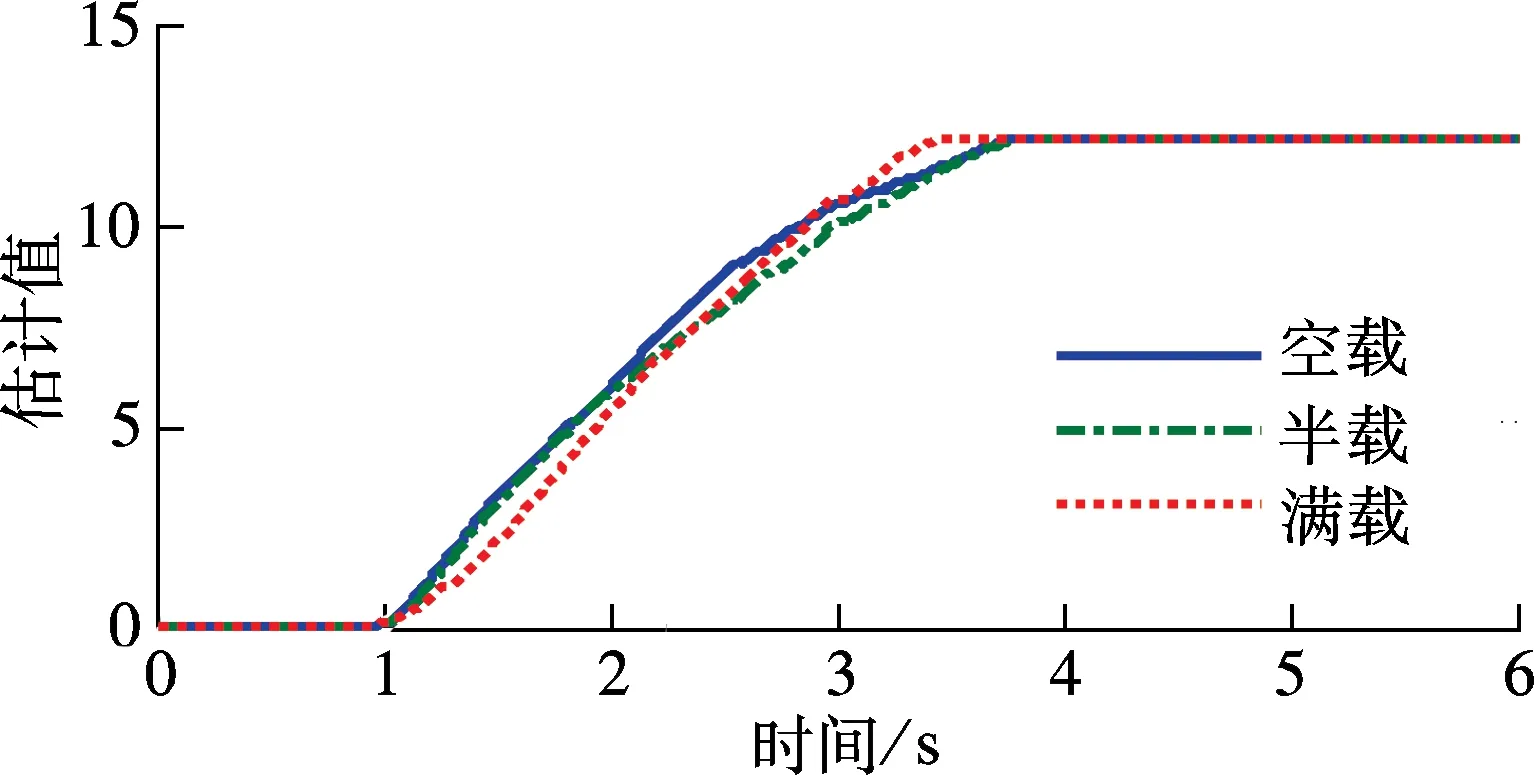
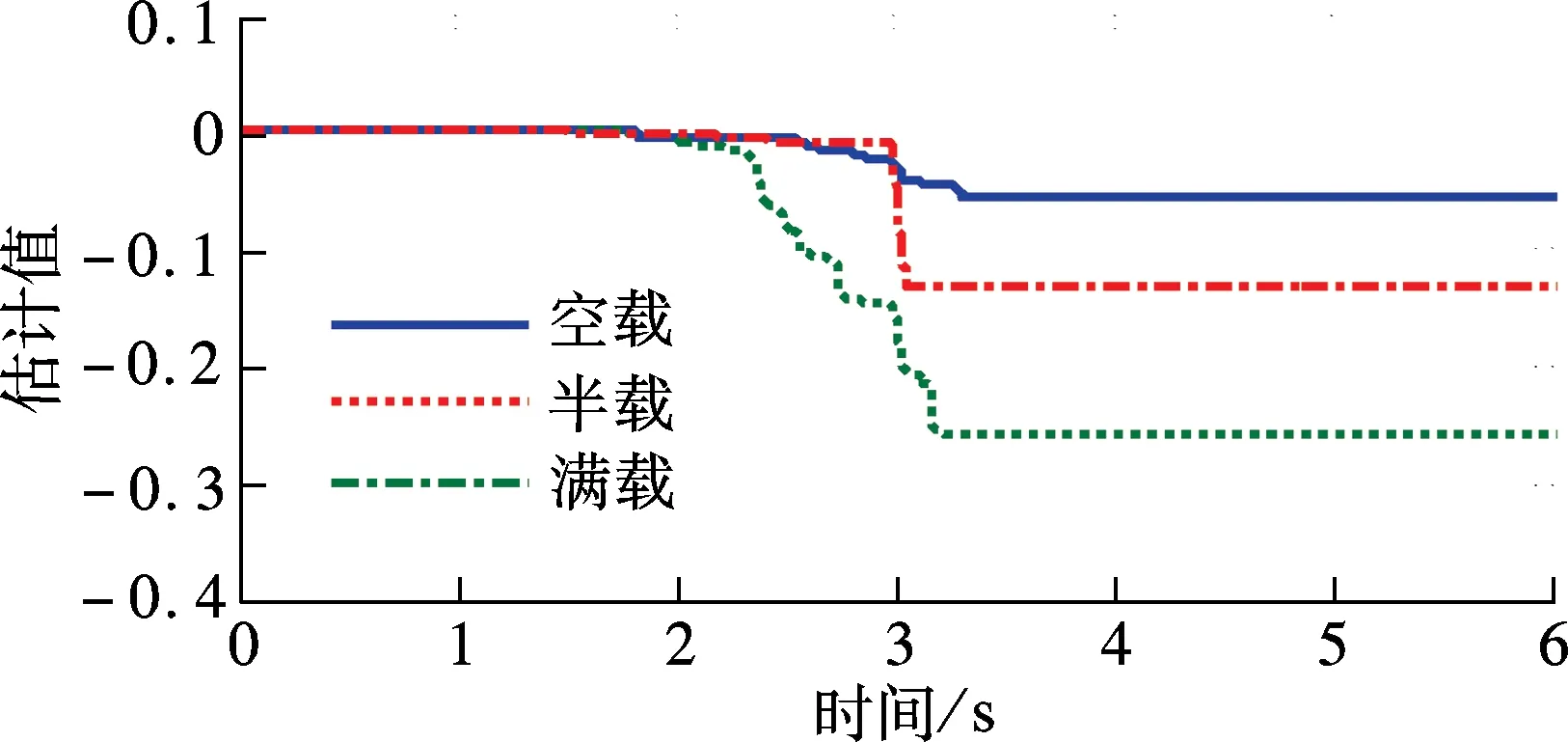
② 0≤s ③ -s1 ④s≤-s1,此时R3被触发,故o1=o2=0,o3=1,s(o1-o3)> 0. 由上述分析可知,对于任意的滑模函数s,有 (12) 定义如下的Lyapunov函数: V1=0.5s2 (13) 将式(5)、(13)对时间求导,并将控制律式(11)代入,令u=u2,可得 (14) 将式(10)和(12)代入式(14),可得 (15) 如果r满足 (16) 考虑如下的自适应模糊滑模控制律: u=u2+ks (17) 式中,k为待设计的控制器参数,且k>0.定义如下的Lyapunov函数: (18) (19) 如果自适应律取为 (20) 将式(20)代入式(19),可得 (21) 故V是非增函数,又因为V(0)有界,故V有界,因此系统所有信号有界.定义非负函数 两边积分可得 故p∈L2.容易验证p的导数存在且有界,即p是一致连续的.根据Barbalat引理,当t→∞时,p→0.因此,当t→∞时,滑模函数s→0,跟踪误差e→0. 为了使控制器的设计过程清晰明了,本文中给出了旋转弹仓的动力学方程(2),但是对于控制器本身是不需要知道弹仓的动力学方程的. 为了保证参数估计的有界性,采用如下的投影算法[16-17]: (22) 旋转弹仓控制系统如图3所示, 永磁同步电机由工作在力矩控制模式下的SolGui 35/60伺服驱动器控制,电流环采样周期为0.1 ms, 驱动器开关频率为20 kHz; 主控制器为贝加莱X20系列高性能控制器CP3485, 采样周期为0.4 ms; 伺服驱动器SolGui35/60与主控制器CP3485之间通过CANopen网络交换数据, 波特率为500 kbit/s. 图3 旋转弹仓示意图 图5为空载、半载和满载3种情况下的位置跟踪误差.可以看出,跟踪误差在学习过程中较大,但很快减小至较小的范围内,并且在3种情况下均获得了很小的稳态误差.随着弹仓参数变化的增大(从空载到半载再到满载),位置跟踪误差也有所增加,但整体来说位置跟踪误差均在较小的范围内. 图4 期望轨迹 (a) 空载 (b) 半载 (c) 满载 (a) 空载 (b) 半载 (c) 满载 (b) α2 (c) α3 以上实验结果说明,本文提出的自适应模糊滑模控制算法不仅对参数变化以及外部扰动不敏感,而且在参数大范围变化时也能获得很高的控制精度. 图6为3种情况下的控制输入.可以看出,控制输入存在不同程度的抖振现象(主要是由测量噪声以及弹仓高速转动时的冲击作用引起的),但是均在可以接受的范围内.当位置跟踪误差接近零时,控制输入不为零,这是主要因为当跟踪误差小到一定程度时,控制输入不足以克服非线性摩擦,因此存在稳态误差,而非零误差使得控制输入不为零. 图7分别为α1,α2,α3的估计值.可以看出,3种情况下的估计值是不同的,可以预见如果使用固定的α1,α2,α3值,当弹仓参数发生较大的变化时,控制性能可能会有所下降,这也是本文把α1,α2,α3作为可调参数的主要原因之一. 本文提出了一种新型的自适应模糊滑模控制方法,根据模糊逼近理论,采用模糊系统逼近未知理想控制律,不需要知道旋转弹仓的动力学方程;采用自适应策略调整模糊系统参数,不仅简化了控制器的设计,而且改善了控制性能.空载、半载和满载3种情况下的实验结果表明,本文提出的自适应模糊滑模控制方法,不仅对系统参数变化以及外部扰动不敏感,而且能够获得很高的控制精度. References) [1]侯保林,马建伟. 链式自动化弹仓的最优保性能控制算法[J]. 兵工学报,2009,30(9):1164-1169. Hou Baolin, Ma Jianwei. Optimal guaranteed cost control algorithm for automatic chain shell magazine [J].ActaArmamentarii, 2009, 30(9): 1164-1169. (in Chinese) [2]马建伟,郭治,侯保林. 旋转弹仓的鲁棒控制器设计[J]. 火力与指挥控制,2006,31(10):15-18. Ma Jianwei, Guo Zhi, Hou Baolin. Robust controller design for mechanized eddy magazine[J].FireControlandCommandControl, 2006, 31(10): 15-18. (in Chinese) [3]张碧陶,皮佑国. 基于分数阶滑模控制技术的永磁同步电机控制[J]. 控制理论与应用,2012,29(9):1194-1198. Zhang Bitao, Pi Youguo. Fractional order sliding-mode control for permanent magnet synchronous motor [J].ControlTheory&Applications, 2012, 29(9): 1194-1198. (in Chinese) [4]Qi Liang, Shi Hongbo. Adaptive position tracking control of permanent magnet synchronous motor based on RBF fast terminal sliding mode control [J].Neurocomputing, 2013, 115: 23-30. [5]Xu Dezhi, Jiang Bin, Qian Moshu, et al. Terminal sliding mode control using adaptive fuzzy-neural observer [J].MathematicalProblemsinEngineering, 2013, 2013: 958958-01-958958-08. [6]Reza Shahnazi, Hasan Modir Shaneci, Naser Pariz. Position control of induction and DC servermotors: a novel adaptive fuzzy PI sliding mode control [J].IEEETransactionsonEnergyConversion, 2008, 23(1): 138-147. [7]Wai R J, Lin C M, Hsu C F. Adaptive fuzzy sliding mode control for electrical servo drive [J].FuzzySetsandSystems, 2004, 143(2): 295-310. [8]Lin C M, Hsu C F. Adaptive fuzzy sliding mode control for induction servomotor systems [J].IEEETransactionsonEnergyConversion, 2004, 19(2): 362-368. [9]Wai R J, Su K H. Adaptive enhanced fuzzy sliding-mode control for electrical servo drive [J].IEEETransactionsonIndustrialElectronics, 2006, 53(2): 569-580. [10]Chaoui H, Sicard P. Adaptive fuzzy logic control of permanent magnet synchronous machines with nonlinear friction [J].IEEETransactionsonIndustrialElectronics, 2012, 59(2): 1123-1133. [11]Nekoukar V, Erfanian A. Adaptive fuzzy terminal sliding mode control for a class of MIMO uncertain nonlinear systems [J].FuzzySetsandSystems, 2011, 179(1): 34-49. [12]Wai R J. Fuzzy sliding mode control using adaptive tuning technique [J].IEEETransactionsonIndustrialElectronics, 2007, 54(1): 586-594. [13]Li Yangmin, Xu Qingsong. Adaptive sliding mode control with perturbation estimation and PID sliding surface for motion tracking of a piezo-driven micromnipulaor [J].IEEETransactiononControlSystemsTechnology, 2010, 18(4): 798-810. [14]Chao Ying. Sufficient conditions on general fuzzy systems as function approximators [J].Automatica, 1994, 30(3): 521-525. [15]Kosko B. Fuzzy systems are universal approximators [J].IEEETransactionsonComputers, 1994, 43(11):1329-1333. [16]Yao Bin,Chang Jiang. Advanced motion control: from classical PID to nonlinear adaptive robust control [C]//The11thIEEEInternationalWorkshoponAdvancedMotionControl. Nagaoka, Japan, 2010:815-829. [17]Chen Zheng, Yao Bin, Wang Qingfeng. Accurate motion control of linear motors with adaptive robust compensation of nonlinear electromagnetic field effect [J].IEEE/ASMETransactionsonMechatronics, 2013, 18(3): 1122-1129. Adaptive fuzzy sliding mode control of rotational shell magazine Zou Quan1Qian Linfang1Xu Yadong1Jiang Qingshan1Yang Huidong2 (1School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China) (2North Automatic Control Technology Institute, Taiyuan 030006, China) An adaptive fuzzy sliding mode control scheme is proposed for the precision position control of rotational shell magazine with meshing impact, large nonlinear friction and wide variations of parameters, etc. The proposed scheme is composed of two fuzzy systems, which are utilized to approximate the unknown ideal control effort and compensate for the approximation error, respectively. Thus, the mathematical model of the shell magazine system does not need to be known and the robustness is good. In the fuzzy approximation system, adaptive mechanism is introduced to online tune the parameters of the fuzzy system, thus the control performance is improved and the robustness is also enhanced. In the fuzzy compensation system, the control effort is auto-tuned according to the sliding variable, then the existence of sliding mode is guaranteed and the chattering phenomenon is reduced. Experimental results under three conditions, i.e., empty-loaded, half-loaded and full-loaded, show that the proposed adaptive fuzzy sliding mode control scheme is insensitive to parameter variations, meshing impact and large nonlinear friction etc. Moreover, the position precision is high. fuzzy logic; sliding mode control; adaptive tuning; rotational shell magazine 2014-07-28. 作者简介: 邹权(1987—),男,博士生;钱林方(联系人),男,博士,教授,博士生导师,lfqian@vip.163.com. 国家基础科研资助项目(A2620133003). 邹权,钱林方,徐亚栋,等.旋转弹仓的自适应模糊滑模控制[J].东南大学学报:自然科学版,2015,45(1):63-68. 10.3969/j.issn.1001-0505.2015.01.012 TP 273 A 1001-0505(2015)01-0063-06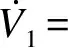
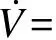
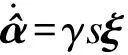
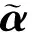
3 实验验证

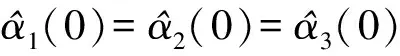
4 结语
