直升机雷达电波传播特性研究

张万泽，李德鑫，魏 鑫，何耀宇

(空军哈尔滨飞行仿真技术研究所，哈尔滨 150001)

【基础理论与应用研究】

直升机雷达电波传播特性研究

张万泽，李德鑫，魏 鑫，何耀宇

(空军哈尔滨飞行仿真技术研究所，哈尔滨 150001)

机载雷达作为提高直升机武器平台作战效能的倍增器，受到各国军队的普遍关注。如何评估其作战效能，提高部队战斗力，是当前亟待解决的问题。在传统波动方程基础上，利用限定上、下传播边界和基于Beilis Tappert平移变换法处理地形要素的宽角抛物方程算法，仿真分析了直升机雷达在标准大气、实际大气和地形遮蔽条件下的电波传播特性。为指挥员进行战场准备，实施正确战略决策提供依据，为评估雷达性能的后续研究提供理论支撑。

电波传播；大气折射；雷达探测；抛物方程

现代高科技局部战争中，直升机作为高效的低空作战武器平台，其作用和优势日渐凸显，受到各国军队的普遍关注。直升机机载雷达经过20世纪70年代的发展、80年代的推广及90年代的普及成为提高直升机武器平台作战效能的倍增器。国内外现役直升机雷达主要有监视雷达、反潜搜索雷达、火控雷达及地形跟随/障碍物回避雷达等[1]，由于技术和经费所限，我国直升机雷达研制较晚，但随着技术和器件的逐渐成熟，产品性能在不断提高。通过研究环境对产品性能的影响，提高作战效能是当前紧迫而又困难的任务。

国内外对于直升机机载雷达作战效能评估的研究成果较少，且传统文献多采用几何计算和概率统计的方法，算法复杂度较高且精度较差。本研究拟采用适合大尺度计算的，基于前向全波法的抛物方程算法，该算法能够处理水平和垂直方向上非均匀分布的大气介质环境，可方便计算地形起伏变化和地表电磁特性变化等条件下的电波传播问题[2,3]。仿真分析了建筑物和地形地貌对武装直升机机载雷达电波传播影响特性，抛物方程方法可以方便快捷的计算出雷达在不同条件下的场分布特性，清晰直观地展现电波受环境影响而产生的折射和绕射效应。

1 抛物方程法

电波传播过程建模中，电场分量ψ(x,z)满足

(1)

二维标量波动方程中，标量ψ为电磁场分量，k=2π/λ为真空中传播常数，n为折射指数。假设大气只随距离(x轴)和高度(z轴)变化，即沿水平方向均匀分布，则ψ与y无关；则水平极化波中只有Ey为非零电场分量(ψ(x,z)=Ey(x,z))，垂直极化波中只有Hy为非零磁场分量(ψ(x,z)=Hy(x,z))。

设e-jkx为电磁场时谐因子，定义沿x轴正向传播的衰减函数为

u(x,z)=e-jkxψ(x,z)

(2)

由此可得到距离-高度二维空间的标量抛物方程，本文采用Feit-Fleck近似法，得到Feit-Fleck型PE方程[4,5]：

ik[n(x,z)-1]u(x,z)

(3)

在直升机作战使用高度范围内，直升机机载雷达的电波传播环境包括对流层大气的上边界和地形地貌的下边界条件，传播影响包括传播媒介的吸收、折射、反射、绕射和散射效应等，实际情况下环境对电波传播的影响是各种复杂效应影响的综合，必须要全面考虑才能够得到较为真实的计算结果。传统方法一般侧重于对单个影响因素的分析，结果误差较大。PE模型可以同时处理复杂大气结构和不规则的地形边界，是目前预测对流层电波传播问题最准确的模型[6]。

1.1 抛物方程上边界条件

抛物方程求解采用的FFT算法虽然可以十分高效的计算场分量，但必须保证电磁波场量在上边界中被迅速衰减，不会向计算域反射或透射出计算域，即必须使电波传播在计算域的有限高度内满足Sommerfeld辐射条件。

对于上边界问题的处理，采用Cosine-taper(Tukey)窗函数

(4)

zmax为计算域最大高度。抛物方程在步进递推求解的过程中，每一距离步进计算的场分量都要乘以吸收层函数W(z)，从而使得计算域0≤z≤0.75zmax高度范围内，计算场保持不变，此范围计算值为准确值；0.75zmax≤z≤zmax高度范围内，受W(z)所限计算场平滑衰减至0，即在最大高度处被完全吸收。因此在设置计算域时，应注意计算域最大高度zmax的取值，若观测高度最大值为zO，为获得精确计算场值，应取zmax≥4/3zO。

1.2 下边界条件

抛物方程下边界为地表与空气的分界面，不规则地形及复杂的地表结构使得抛物方程下边界条件变得十分复杂，在研究对流层电波传播问题时，通常使用阻抗边界条件描述电磁场在地表边界的传播特性。

抛物方程的数值计算可以通过离散正弦变换(DST)或离散余弦变换(DCT)实现，可明显提高算法计算效率。假设地表边界近似为理想PEC平面，根据镜像理论对于水平极化波，u对应于Ey分量，在z=0处满足Dirichlet边界条件，即u(x,0)=0，且相对于z=0为奇函数，u(x,-z)=-u(x,z)。下边界条件电磁波为水平极化时，对于u(x,z)的傅里叶变换式变为

(5)

(6)

定义正弦变换和余弦变换为

(7)

对于理想PEC平面，SSFT算法可以利用快速正弦(FST)或快速余弦算法(FCT)实现，从而提高算法计算效率。

对于实际情况，地表面边界条件不可能是理想PEC平面，有限阻抗表面边界通常用Leontovich阻抗边界条件描述

(8)

表面边界阻抗特性用α表示，水平极化和垂直极化条件时，有

(9)

εC为边界面相对复介电常数，计算式为

εC=εs+60δsλi

(10)

εs和δs分别是边界表面的相对介电常数和电导率，λ为电波波长，θi是第i步进的传播仰角(即掠射角)。

假设

(11)

对于水平极化波，可用w(x,z)的正弦变换等效阻抗边界条件下u(x,z)的傅里叶变换。其物理意义为，场分量为u(x,z)的电磁波在有限阻抗边界表面上的传播问题可以等效为场分量为w(x,z)的水平极化电磁波在PEC表面边界上的传播问题。因此，可将SSFT等效为混合了正弦变换和余弦变换的形式，即混合傅里叶变换。

对式(11)两边进行正弦变换，分步积分并整理得到混合傅里叶变换MFT。

U(x,p)=JMFT[u(x,z)]=

(12)

(13)

(14)

将折射指数视为常数，利用分步积分法可得

(15)

将变换式(12)、式(13)应用到式(15)中，可得

(16)

2 大气折射指数

对于地球表面大气折射率，本研究采用国际电讯联盟(ITU-R)规定计算PE方程中的n值[6]

N(z)=106×(n-1)=300e-0.139z

(17)

式中，z为观测点海拔高度(km)。

对于精细化评估，可采用探空气球或气象站数据情报支持，利用实测数据构建相关的修正折射指数模型，带入折射效应因子n中即可计算出真实大气条件下的电波传播特性。

3 地形遮蔽效应

抛物方程模型处理不规则地形边界时，一般要通过数学模型将不规则地形转化为平地面边界，从而将不规则阻抗边界转化为平面阻抗边界，模型复杂度高在实际情况下难于求解。下面从Beilis Tappert平移变换法出发，利用分段线性边界平移法推导出适合抛物方程算法的地形处理模型。

利用Beilis Tappert地形模型在计算域地形剖面上建立新坐标系，通过坐标变换将不规则地形上的抛物方程模型转换成平地面的形式。以连续函数z=T(x)=t(x)-x2/(2ae)描述不规则地形剖面，t(x)为描述地形起伏的函数。以不规则地形某点作为坐标原点，建立新坐标系x′o′z′满足

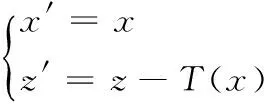
(18)

新坐标系下的波动方程式(1)变为

(19)

利用Feit-Fleck近似法，推导出Beilis Tappert地形模型下的Feit-Fleck型宽角抛物方程

(20)

与式(3)相比，两者仅相差在折射指数项，不规则地形表面上的平地面近似模型修正折射指数为

(21)

则地形要素条件下的抛物方程模型为[5-6]

(22)

当地表边界为无起伏波动的平面边界条件时，即∂2T/∂x′2=0，式(22)与式(16)一致。地形要素并不影响抛物方程的绕射因子项，仅改变折射因子项。因此，地形遮蔽条件下的抛物方程MFT解与式(16)形式一致，仅改变折射因子项R=eik[mT(x′,z′)-1]Δx。

4 仿真分析

利用宽角抛物方程模型计算水平极化条件下某型直升机雷达在标准大气、实际大气和地形遮蔽条件下视距传播时的场分布特性。

直升机雷达基本参数如表1所示。

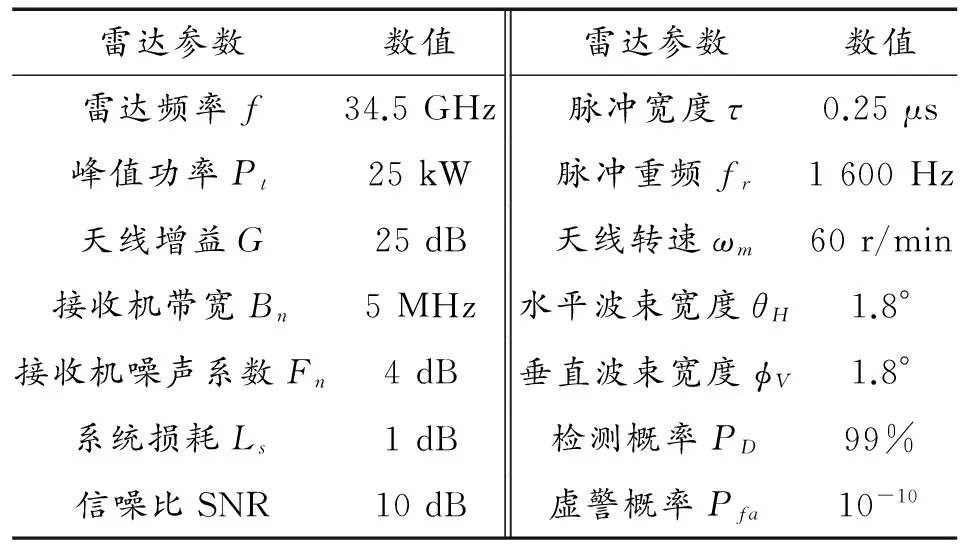
表1 直升机机载雷达基本特性参数

选取理想条件城市地表下边界和实际复杂大气真实地表下边界2种条件，计算环境对直升机雷达电波传播特性的影响效能。

仿真条件1：标准大气条件下(图1)，由距离雷达初始坐标2 km和5 km处，投影宽度80 m和30 m的2个建筑物构成的城市地表下边界条件。地面介电常数εr=4，导电率σ=7.5×10-4S/m，雷达高度200 m，观测距离10 km。

仿真条件2：从大气数据库中选取2013年4月5日数据作为传播环境大气条件，如图4所示。利用美国太空总署(NASA)和国防部国家测绘局(NIMA)联合测量的SRTM(Shuttle Radar Topography Mission)数据作为地形数据库，抽取SRTM3高程数据中E119°35′14″、N32°9′17″至E119°40′15″、N32°6′1″段的地形数据作为计算域下边界条件，地貌多为森林和植被，地面介电常数εr为10～30，导电率为10-3～3×10-2S/m，为方便比对，雷达高度和观测距离设置与仿真条件1相同。

由仿真计算图1～图6可以看出，抛物方程方法可方便、快捷的计算大气和地形地貌条件对电波的传播、反射、散射和绕射影响，并可利用传播因子清晰直观地展现雷达电波的传播场分布特性。利用计算所得的电波传播因子，可方便计算电波传播的衰减特性，利用雷达效能评估模型分析自由空间传播损耗对于雷达性能的影响。

图1 标准大气修正折射率

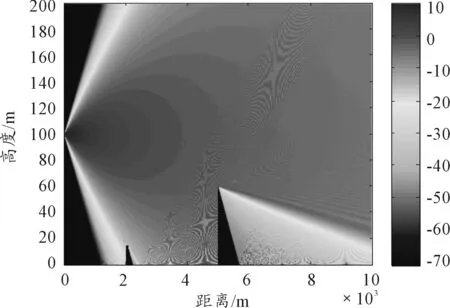
图2 雷达电波传播因子分布

图3 传播距离为4,6和8 km处传播因子剖面图

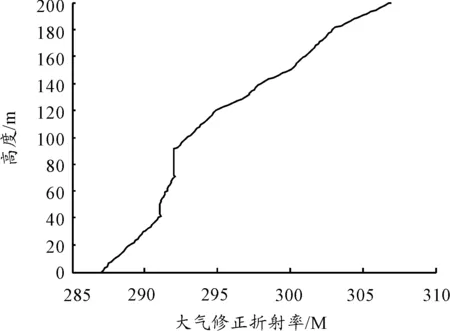
图4 2013年4月5日大气修正折射率

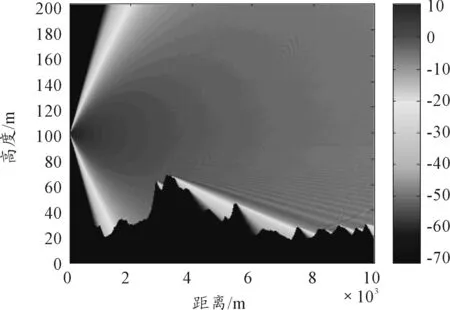
图5 复杂环境下雷达电波传播因子分布

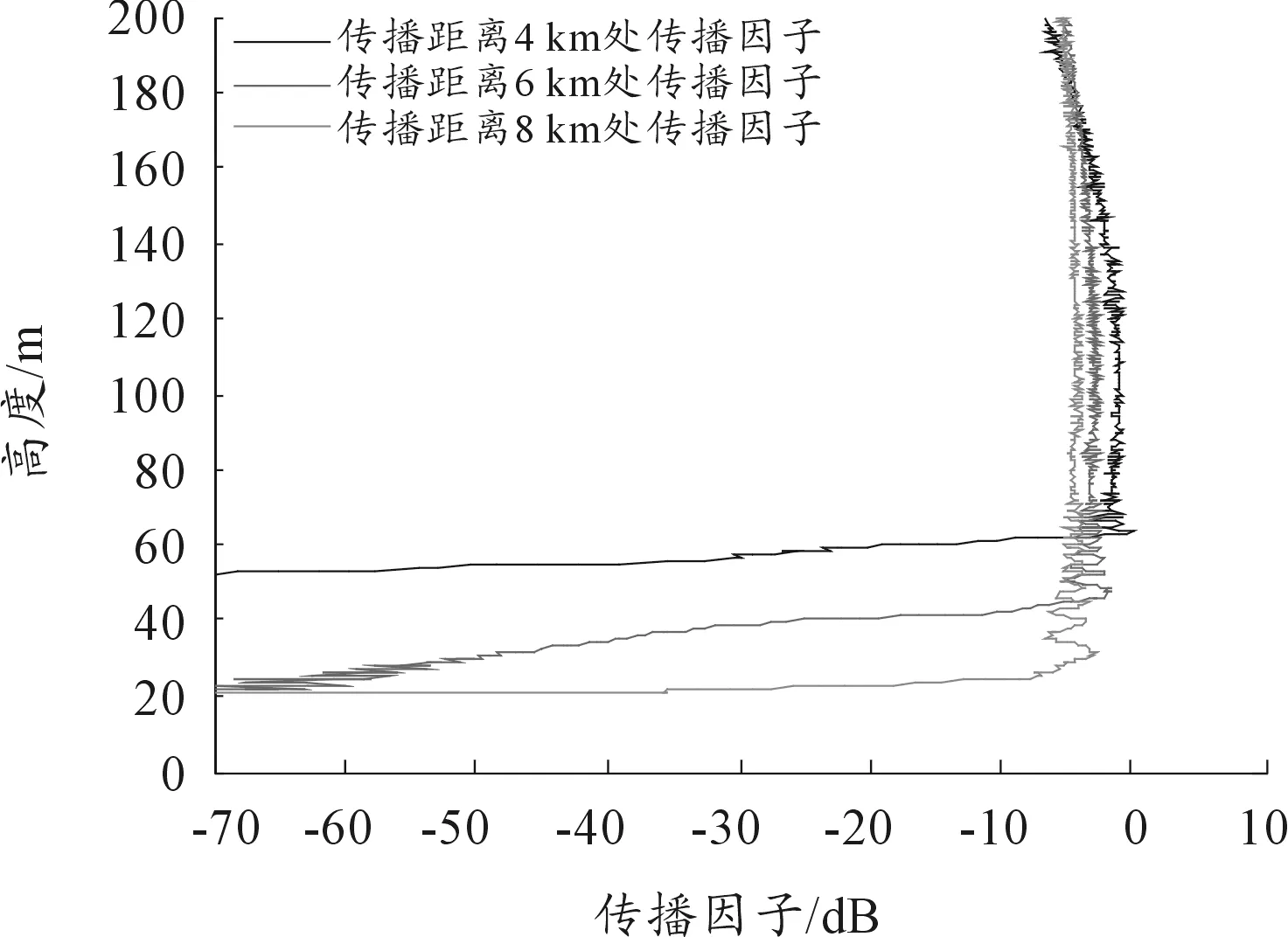
图6 复杂环境下不同距离处传播因子剖面图

对比两次仿真实验，由于武装直升机作战使用高度较低，大气环境对于雷达的使用影响较小，而地形地貌对雷达的作战效能影响较大。与图6相比，图3中100～200 m高度区间电波传播因子分布有强烈的震荡，这是由于仿真条件设定的城市干土下边界对雷达电波的反射效应，反射波与直射波之间的干涉叠加造成的，这种叠加效应会增加雷达解算参数误差。森林和植被组成的地貌对于高频段电磁波吸收衰减效应明显，雷达反射能量影响较小。地形对雷达电波传播的遮蔽效应会导致雷达盲区，由于直升机火控雷达为较高频段的Ka波段，地形劈尖绕射效应不明显，主要为通视性影响。

通过分析雷达电波传播特性，趋利避害可增进武器作战效能，从而提高航空兵作战能力，与此同时可合理利用环境对敌方武器作战效能的影响，合理排兵布局，消减敌方战力。

需要指出的是，本研究未考虑烟尘、气溶胶等环境因素对电波传播的影响，后续工作可在分析雷达效能评估模型中加入其他环境衰减因子项，通过分析环境因子吸收衰减和反射、散射的影响机理，评估环境要素影响下的雷达性能。

实验过程中，仅有雷达附近的大气数据，缺少雷达至目标间的环境数据，数值计算假设大气水平均匀分布必然会引起理论计算值与实际测量值间的差异；传播路径上地面边界以地形数据库和航拍图片为参考，而传播路径地貌属性不可能相同，不同地表吸收散射衰减必然会对实验结果带来误差。后续工作应包括环境数据库的充实和修正，精确的情报数据可提高算法计算精度和效率，是评估策略的基本保障。

5 结束语

在传统波动方程法基础上，利用宽角抛物方程算法仿真分析了直升机雷达在标准大气、实际大气和地形遮蔽条件下的电波传播特性。该模型可以同时处理复杂的大气结构和不规则的地形边界，可以方便快捷的计算出雷达在不同条件下的场分布特性。利用该算法可仿真模拟复杂条件下的直升机雷达无线电波传播特性，评估直升机雷达在复杂环境下的作战性能，为辅助决策和深化研究提供理论基础和借鉴依据。

该方法在研究高频率、大尺度条件下的电波传播问题时，计算开销巨大，不具备实时性；同时受自身二维建模基础所限，无法计算三维复杂地形条件下的电波传播特性，对低空高强度复杂环境下作战的直升机雷达进行评估的精确性不高。因此，后续工作包括并行处理算法和三维地形处理等算法的研究。

[1] 郑敏，周琪，赵玉洁,等.国外直升机机载雷达的现状与发展趋势[J].直升机技术,2003 (4):42-48.

[2] 李德鑫,杨日杰.水平非均匀大气条件下的抛物方程模型研究[J].宇航学报,2011,32(7):1569-1575.

[3] 李德鑫,杨日杰.不规则地形条件下双向DMFT电波传播特性算法研究[J].航空学报,2012,33(2):297-305.

[4] Feit M D,Fleck J A.Light propagation in graded in-dex fibers[J].Applied Optics,1978(17):3993-3998.

[5] Levy M F.Parabolic equation methods for electromagnetic wave propagation [M].London:IEE Press,2000.

[6] 熊皓.无线电波传播[M].北京:电子工业出版社,2000.

(责任编辑 唐定国)

Researching on Radio Wave Propagation Characteristics of Helicopter Radar

ZHANG Wan-ze, LI De-xin, WEI Xin, HE Yao-yu

(Flight Simulation Research Institute of Air Force, Harbin 150001, China)

The airborne radar was general concerned as a multiplicator to improve the operational effectiveness of military helicopter by many countries’ Army. The current serious problems were how to evaluate their operational effectiveness and improve combat effectiveness. The helicopter radar radio wave propagation characteristics in the conditions of standard atmosphere, the real atmosphere and terrain masking were analyzed by the wide-angle parabolic equation algorithm based on the traditional wave equation, limited propagation boundaries and the Beilis Tappert translation method. The theoretical support was provided for the battlefield commanders to prepare for the battle and make the right strategic decision, meanwhile, for the follow-up study to evaluate the performance of the airborne radar.

radio propagation; atmospheric reflection; radar detection; parabolic equation(PE)

2015-03-09

泰山学者建设工程专项经费资助、国家自然科学基金(61002006)

张万泽(1970—)，男，工程师，主要从事战场环境仿真研究；李德鑫(1983—)，男，博士，工程师，主要从事飞行仿真研究。

10.11809/scbgxb2015.08.039

张万泽，李德鑫，魏鑫，等.直升机雷达电波传播特性研究[J].四川兵工学报，2015(8):157-161.

format:ZHANG Wan-ze, LI De-xin, WEI Xin, et al.Researching on Radio Wave Propagation Characteristics of Helicopter Radar[J].Journal of Sichuan Ordnance,2015(8):157-161.

TN951；TJ01

A

1006-0707(2015)08-0157-05