基于谐波小波带通滤波的动不平衡信号提取研究
2015-05-05冯英鹏占小杰李传江
冯英鹏,占小杰,李传江
(上海师范大学信息与机电工程学院,上海200234)
0 引言
动平衡测量系统是通过安装在两侧硬支承上的传感器测量振动信号的,后经信号转换、调理、传输以及分析等多个环节完成动不平衡信号(即有用信号)的测量[1]。而且这个动不平衡信号提取的越精确,就越能保证转子系统的动平衡。为此,研究一种高效可行的动平衡测量方法,既能保证信号相位的不偏移,又能准确测定不平衡量的幅值,具有十分重要的现实意义。而谐波小波滤波方法有着明确的表达式、时频分解灵活、盒形紧支谱以及相位锁定特性[2-3],基于上述优点,将谐波小波带通滤波方法用于动不平衡信号的提取,研究表明该方法有效可行,可以消除噪声干扰。
1 谐波小波滤波原理
一种复小波,可以将信号毫无遗漏地分解到相互独立的频段。这样特定频率成分与其他频率成分被分离,从而消除了其他频率成分对该频率段的影响,那么被淹没的微弱信号得以体现,可以说是信噪比得到提高[2]。于是,研究某一信号特定频率成分时可采取对该信号进行谐波小波分解,将其他频段的谐波小波系数置零,保留特定频段的小波系数,然后对其重构,如图1所示。根据正交性可知,重构后的信号只包含特定频率成分,其余成分被滤除,即实现了精确滤波的目的[4]。

图1 信号谐波小波分解重构流程
谐波小波在频域具有明确的表达式,设有实偶函数he(t)和实奇函数ho(t),其傅氏变换为:

把 He(ω)和 Ho(ω)组合得到

即为谐波小波的频域表达式,从图2看到,H(ω)具有极好的紧支特性,并且有着严格的盒形特性,非常适合用于信号滤波,提高信噪比。
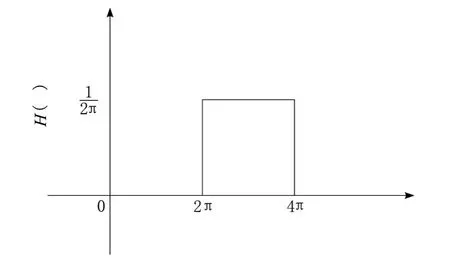
图2 谐波小波函数的频域波形
对H(ω)做傅里叶逆变换,可得到谐波小波

其实部与虚部如图3所示,可见h(t)具有很好的紧支特性。

图3 谐波小波函数实部与虚部形状
对谐波小波函数进行伸缩平移,令t=2jt-k(j,k均为整数),式(4)变为:

而h1(t)的傅里叶变换为:

令p=2jt-k,dt=2-jdp,则
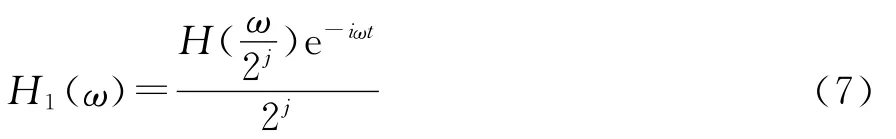
与式(3)比较发现,H1(ω)频谱为发生改变,只是水平方向上的尺度压缩了2j,在新的尺度上平移了k个单位。j的值与小波的层有关,标准的谐波小波频谱2π~4π对应j=0,于是得到第j傅里叶变换频谱区间为2j+1π~2j+2π,j值越大,频带带宽越宽,不同层上的谐波小波频谱区间如图4所示。

图4 不同j值时谐波小波的频谱
从图4可以看出,谐波小波对信号的分解频带宽度从高频到低频以关系递减。令m=2j,n=2j+1,m,n∈R+,且m<n,式(3)可化为:

其对应的时域表达式为:

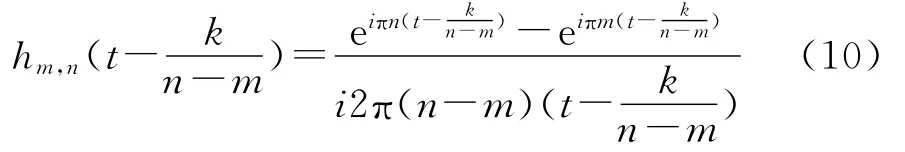
鉴于谐波小波函数族中层层之间都是正交的,所以可把谐波小波作为基函数系,这样就能将信号正交、无遗漏地分解到相互独立的空间,实现信号分解到不同频段,方便精确研究单一频率信号,提取信号特征。其实部与虚部都可作为零相移滤波器,使得谐波小波具有相位锁定功能,它能克服基于二进小波信号分析频域产生相位移动导致提取特定频率信号的不精确问题。所以在转子动平衡中,应用谐波小波带通滤波算法提取动不平衡信号可以保证信号的相位不失真,提高提取精度。
即工程中常用的分析中心在
2 谐波小波滤波方法的仿真研究
谐波小波分解算法是通过FFT和IFFT实现的,具体步骤如下:
a.对振动信号f(t)进行FFT,得到其频谱Fk,k=1,2,…,N,N=2n。
b.选择分解尺度,对谐波小波函数hm,n(t)进行FFT得到频谱Hk,k=m,…,n。
c.计算Fk与Hk的乘积,做IFFT得到谐波小波分解系数,即目标频率的信号。
2.1 谐波小波算法提取微弱模拟信号
为了验证谐波小波带通滤波的性能,现对一模拟信号进行滤波分析。假定模拟信号包含10Hz,80Hz和160Hz三种频率的信号[3,5],则
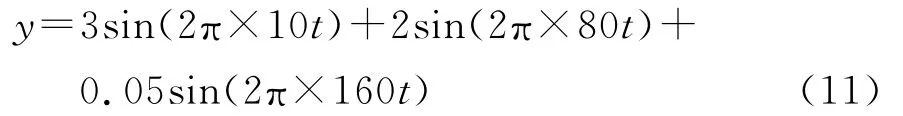
在Matlab仿真平台中,采样频率选择fs=4 096,采样点数为N=2 048,利用谐波小波算法对其分析。因为160Hz频率的信号幅值远小于前两者,所以在信号的频谱中几乎看不到谱峰,属于微弱信号。
通过选择不同的谐波小波分解尺度,在[8,12]、[78,82]、[158,162]频段分别提取这三种频率的信号,再对滤波后的信号频谱经IFFT即可获得各频率信号波形,即便是频率为160Hz的微弱信号,经谐波小波带通滤波后其信号波形十分明显[3,5]。分析发现,得到的信号波形正好与其频率相吻合,且在频域内并无相位移动,有利用信号的提取,可防止信号检测的误判,可见谐波小波带通滤波算法较其他方法具有优势,能很好地提取特定频率的信号。
2.2 谐波小波算法实际应用研究
实验平台采用上海欧承动平衡机有限公司提供的转子动平衡机,左右支撑点处安装压电陶瓷加速度传感器,变频调速驱动,测试平台采用标准转子(3 kg)[6]。实验中,转子转速设定为1 680r/min(转子频率为28Hz),现场采集的转子动不平衡信号如图5所示。从图中可以看到,由于机器振动、随机噪声以及环境等因素的存在,尽管经过硬件电路滤波,转速信号微弱,淹没于噪声中,不易分辨。选择采样频率fs=512,分析频率fH=256Hz,对转速信号进行FFT,从频谱中看到信号含有强烈的低频噪声干扰,这是由转子低速运行引起的,有用的信号几乎看不到如图6所示。为了提取28Hz的频率信号,采用小波包和谐波小波算法进行分解。
小波包采用‘db4’小波对信号进行5层分解,带宽为4Hz,信号频段为28~32Hz,滤波后的频谱图如图7所示,可以看到该频段内包含较多其他频率信号的谱峰。利用谐波小波带通滤波算法,调节带通滤波器的上下限频率,信号频段设为27~29Hz,滤波后的频谱图如图8所示,较图7,谐波小波提取的信号频谱所含成分较少。
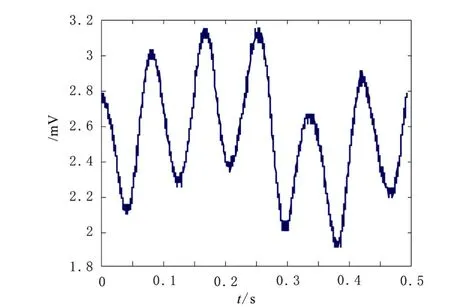
图5 现场采集的动不平衡信号

图6 动不平衡信号的频谱
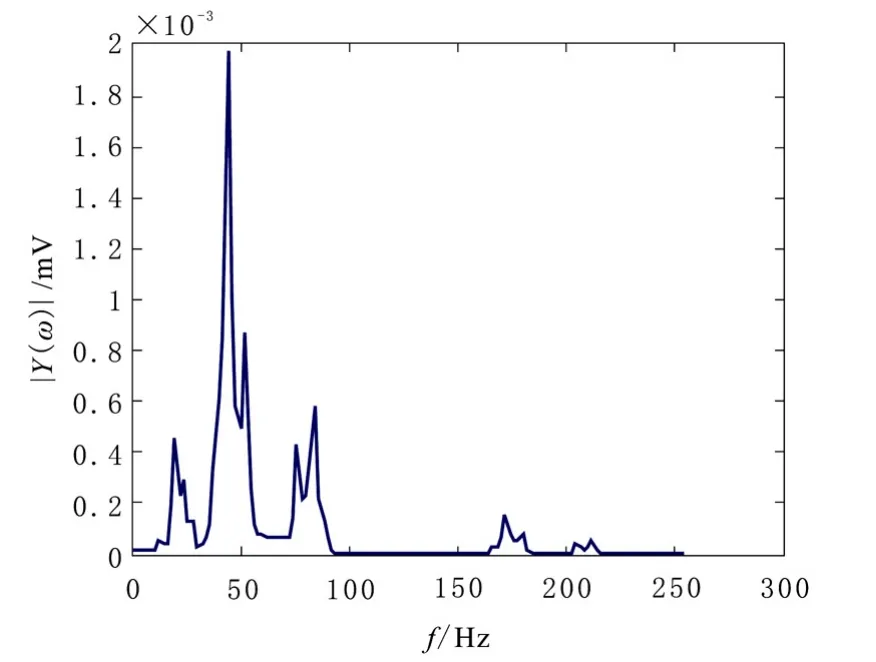
图7 小波包提取的信号频谱

图8 谐波小波提取的信号频谱
对图8中得到的数据进行重构,重构后的信号波形如图9所示。经分析,谐波小波算法提取到了与转子转速同频的振动信号。

图9 谐波小波提取到的转子转速(1 680r/min)信号
3 结束语
谐波小波带通滤波算法具有相位锁定和盒形谱特性决定了它适合于动平衡测量系统的动不平衡信号提取,且构造简单,有着明确的数学表达式。该方法根据信号的相关性,由转动频率和滤波带宽确定出相应频段的谐波小波,后经滤波、重构即可精确提取出淹没在强噪声中的动不平衡信号,解决常规滤波方法滤波精度不高的问题。
[1] 夏耀曾,崔凤奎.谐波小波在动不平衡信号提取中的应用[J].噪声与振动控制,2009,29(1):65-68.
[2] 卿湘运,段红,魏俊民.谐波小波在动平衡机不平衡量信号提取中的应用[J].浙江工程学院学报,2003,20(2):100-103.
[3] 李瞬酩,许庆余.微弱振动信号的谐波小波频域提取[J].西安交通大学学报,2004,38(1):51-55.
[4] 郑云飞,童军,刘晓丹.谐波小波在发动机振动信号分析中的应用[J].噪声与振动控制,2008,28(6):24-28.
[5] 陈果.一种改进的谐波小波及其在转子故障诊断中的应用[J].机械工程学报,2011,47(1):8-16.
[6] 李传江,费敏锐,胡豁生,等.基于谐波小波和Prony算法的转子不平衡信号提取[J].仪器仪表学报,2014,33(11):2516-2522.
