基于阈值改进的DFT信道估计算法

吴君钦,黄茜茜

(江西理工大学 信息工程学院，江西 赣州 341000)

基于阈值改进的DFT信道估计算法

吴君钦,黄茜茜

(江西理工大学 信息工程学院，江西 赣州 341000)

针对正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)系统中，基于离散傅里叶变换(Discrete Fourier Transform，DFT)的信道估计算法未抑制循环前缀之内的噪声的问题，设置时域阈值可以有效地抑制该部分噪声。鉴于一些文献的阈值算法存在不足，提出将噪声样本点能量升序后，取中间部分样本点的能量平均值并乘以适当系数，作为新的阈值。仿真结果表明，改进的算法能够进一步抑制该部分噪声，性能得到了提高，但增加的计算量较小。

正交频分复用；信道估计；离散傅里叶变换；循环前缀；阈值

OFDM技术一直是通信研究的热点，是一种很具潜力的通信技术。OFDM技术具有高效的传输速率，频谱利用率高，很好地对抗频率选择性衰弱和窄带干扰等优点，因此适用于多径衰落信道的高速数据传输通信系统[1]。为获得较高的频谱利用率，需要通过估计衰弱信道的参数来进行相干检测和解调[2]。因此，信道估计是OFDM系统的关键技术，也是通信领域研究的热点之一。

信道估计有很多种方法，主要有非盲估计、盲估计和介于二者之间的半盲估计。非盲估计是利用导频得到导频位置的信道信息，然后通过插值得到整个信道信息。它主要有最小平方(Least-Square，LS)估计、最小均方误差(Minimum Mean Square Error，MMSE)估计和基于DFT的信道估计。一般地，LS估计算法比较简单，它的计算量小，复杂度低，但是均方误差很大。MMSE估计具有很高的估计精度，但是需要预先知道信道的统计特性，并且在实际系统中很难得到这些先验信息，计算复杂度高，因此不适合实际系统的应用[3]。DFT算法是将LS估计得到的信道频率响应经过离散反傅里叶变换(Inverse Discrete Fourier Transform，IDFT)，得到信道冲激响应(Channel Impulse Response，CIR)，根据OFDM系统中CIR不小于保护间隔(guard interval，GI)的原理，将CIR大于循环前缀的部分置为零，保留循环前缀内的CIR，再经过DFT变换得到频域的信道响应。DFT算法不仅不需要知道信道的统计信息，而且还可以利用快速傅里叶变换(Fast Fourier Transform，FFT)来减少运算量，比MMSE算法简单，更容易实现，而且估计性能比LS算法好。

然而DFT算法只是去除了循环前缀之外的噪声，并没有考虑循环前缀之内的噪声，所以为了去除这部分噪声，很多文献提出了各种基于时域阈值去噪的估计方法。文献[2]提出的阈值可以有效地滤除一部分噪声，但是它是针对CIR长度已知的系统，而且性能受突发大脉冲噪声的影响会比较大。文献[4]提出的阈值算法只适用于稀疏矩阵，而且和文献[5]都需要对信噪比进行估计，增加了计算复杂度。文献[6-7]是利用小波分解的方法来进行阈值去噪，然而复杂度较高，效果不是很明显。鉴于以上方法的不足，本文提出一种基于改进阈值的DFT估计算法，将循环前缀之外的噪声样本点能量进行排序，选取中间合适长度的一段样本点能量的平均值，并乘以适当系数作为新的阈值。从仿真结果看，改进算法在误比特率(BER)和均方误差(MSE)这两个方面都得到了明显的改善。

1 系统模型

本文研究的是基于导频的OFDM基带系统，信道模型是时变的多径瑞利信道，系统模型如图1所示。

图1 OFDM系统中基于导频的信道估计的基带模型

假设OFDM系统总子载波数为N，每个子载波由数据信号X(k)组成。经过IDFT后得到的时域信号为

(1)

信号通过多径衰落信道后，在接收端得到输出响应可表示为

y(n)=x(n)*h(n)+w(n)

(2)

式中：*代表卷积；h(n)是信道冲激响应；w(n)是加性高斯白噪声；h(n)表达式为

(3)

式中：L是多径信道的径数；αi和λi分别是第i径复信道的增益和延时。一般的，信道时延不超过CP的长度。

经过IDFT后，频域系统表示为

Y(k)=X(k)H(k)+W(k),0≤k≤N-1

(4)

式(4)也可用矩阵形式表示为

Y=XH+W

(5)

式中：X是由发送数据组成的对角矩阵，X=diag(X1,X2,…，Xn)，Y,H,W都是N×1的列向量。

2 信道估计方法

2.1 基于LS的信道估计

本文研究的OFDM系统是基于块状导频，即训练符号上所有子载波都传输着导频信号。对训练符号进行FFT变换，得到频域的接收信号，LS估计表达式[8]为

(6)

从式中可看出，LS估计结构简单，计算复杂度低。但是每个子载波上都带有一个高斯噪声项，可见LS估计的MSE比较大。

2.2 DFT信道估计

DFT估计是在LS估计的基础上，将得到的频域信道响应通过IFFT得到时域信道响应，把循环前缀之外的部分置为零来实现噪声的消除。算法框图如图2所示。

图2 DFT算法框图

算法的具体步骤如下：

1)将LS估计得到的信道频域响应进行N点IDFT转换到时域，得到第n个样点的CIR

(7)

式中：0≤n≤N-1，w(n)=IDFTN{W(k)/X(k)}，下标N代表N点IDFT变换。一般的，由于CIR的长度小于循环前缀的长度，并且远小于子载波的个数，将CIR分为两部分[9]，一部分包含了所有信道信息的前L(一般取循环前缀的长度)个抽样点，另一部分都是噪声点，即

(8)

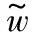
(9)

3)然后对上式做DFT变换到频域，最后得到DFT估计为

(10)

从以上步骤，可以看出DFT估计算法消除了循环前缀之外的噪声，性能比LS估计有很大提高。

3 基于改进阈值的DFT信道估计

上文介绍的DFT估计算法只滤除了循环前缀之外的噪声，为了提高它的估计性能，必须尽可能地消除循环前缀里的噪声。在循环前缀之内，信道响应能量只是存在于少数样本点上，而其他的为噪声样本点，因此，设置一个阈值门限将能量点和噪声样本点区分开来是必须的。通过设置时域阈值，将大于阈值的样本点保留，小于阈值的样本点置零，这里不排除会误滤除一些幅值较小的能量点，但是对于系统来说影响很小，可以忽略。所以在时域内，当0≤n≤N-1时，阈值处理得到

(11)

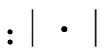
(12)

最后对式(12)做FFT变换，就可以得到改进算法的频率信道响应估计。

综合上述步骤，可以看出阈值λ的确定是改进算法提高估计性能的关键之处。因此，必须通过选择最佳的阈值来实现尽可能滤除噪声而又保留大部分有用CIR的最优估计性能。

文献[2]提出的阈值应用最为广泛，它是取循环前缀之外的样本点能量平均值的两倍作为阈值，其表达式为

(13)

但是实际信道一般是非整数采样，在循环前缀之外也会有一些能量较大的有效样本点，而且当有突发脉冲噪声影响时，都会导致阈值偏大，滤除了一些能量值较小的有效样本点，误差比较大。

文献[10]针对上述问题，首先将循环前缀之外的最大样点值作为阈值，即

(14)

式中：max函数意义是取最大值。但是为了防止突发大脉冲对系统的影响，继而将式(13)和式(14)做平滑，平滑系数为α，则最后提出的阈值为

λ3=aλ2+(1-a)λ1

(15)

该算法在一定程度上比文献[2]提高了估计性能，对突发大脉冲的影响也有一定缓解。但是这里提出的阈值一部分取了样本点的最大值，如果最大值幅值偏大，会把较多能量偏低的样本点滤除掉，所以不适合循环前缀之外有较多幅值偏大的能量样本点的情况，在实际应用中不是最优阈值。

鉴于上述文献所提出阈值的不足，本文提出一个新阈值，将时域里L到N-1之间的噪声样本点能量进行升序排序，取中间适当区域的样本点能量平均值，再乘以适当系数作为新的阈值，可表示为

(16)

式中：0≤n≤N-1，β为适当系数，sort是排序的函数。这里提出的阈值不会受幅值偏大的样本点影响，而且当有突发大脉冲噪声时，阈值变大的幅度很小，甚至可以忽略不计，尽可能地避免滤除到有效样本点，提高了估计的准确性。

4 仿真结果分析

本文仿真采用的是16QAM调制的OFDM系统。采用块状导频结构，假设系统收发同步。仿真参数设置：子载波数为200，循环前缀长度为100，导频间距为10，每个数据帧有5个数据符号，总共传输50个数据帧。信道采用多径瑞利信道模型，多径数为6。本文改进算法的适当系数β取3，b取29。本文从误比特率(BER)和均方误差(MSE)这两方面来比较上文给出的LS算法、DFT算法、文献[2]改进的DFT算法、文献[10]改进的DFT算法和本文基于阈值改进的DFT算法的性能。仿真结果如下，表1为各种估计算法的仿真运行时间表，图3为各个算法的BER对比曲线，图4为各个算法的MSE对比曲线。

表1 各种估计算法的运行时间统计

算法算法运行时间/sLS估计00011DFT估计00012文献[2]改进DFT估计00013文献[10]改进DFT估计00013本文改进DFT估计00014

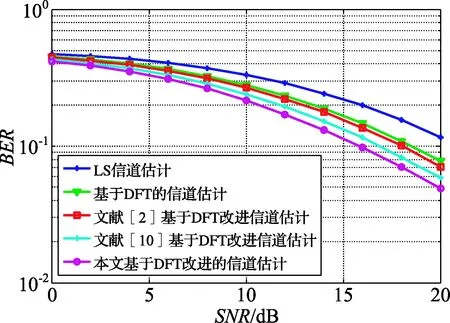
图3 各算法的BER曲线

图4 各算法的MSE曲线

由表1并结合公式(13)、(15)、(16)可以看出，本文改进算法的计算量主要是在排序的过程有所增加，排序算法的平均时间复杂度为O(n2)。总体来说，增加的计算量很小。由图3和图4可以看出，LS算法的BER和MSE都很大，性能最差。DFT算法比LS算法性能有所提高。基于DFT改进的3种算法，进一步滤除了循环前缀之内的噪声，性能较传统DFT算法都有提高，并且本文改进的算法估计性能最好。

5 总结

本文介绍了基于导频的信道估计方法，LS估计算法虽然计算简单，但是误差很大。DFT估计算法有效地提高了估计的性能，但是并没有滤除循环前缀内的噪声。基于这一点，设置阈值门限来抑制该部分噪声，并且本文提出了不同于以往文献的新阈值，使性能得到了很大提高。仿真结果表明，本文提出的基于阈值改进的DFT估计算法比LS估计算法、DFT估计算法、文献[2]和文献[10]的阈值算法，在BER和MSE两方面都有更优越的估计性能，并且增加的计算量较小。

[1] 郭锐. 一种基于DFT的LTE下行信道估计算法[J].北京联合大学学报：自然科学版，2011，25(2)：20-23.

[2] KANG Y，KIM K，PARK H. Efficient DFT-based channel estimation for OFDM systems on multipath channels[J]. Communications IET，2007，1(2)：197-202.

[3] 董小平，王荆宁. 基于DFT的信道及噪声估计算法分析[J]. 无线电工程，2012，41(12)：12-14.

[4] OLIVER J，ARAVIND R，PRABHU K M M. Sparse channel estimation in OFDM systems by threshold-based pruning[J]. Electronics Letters，2008，44(13)：830-832.

[5] ROSATI S，CORAZZA G E，VANELLI-CORALLI A. OFDM channel estimation with optimal threshold-based selection of CIR samples[C]//Proc. IEEE Global Telecommunications Conference. [S.l.]：IEEE Press，2009：1-7.

[6] LEE Y S, SHIN H C, KIM H N. Channel estimation based on a time-domain threshold for OFDM systems[J]. IEEE Trans. Broadcasting，2009，55(3)：656-662.

[7] WANG Xiaoqing，WANG Jintao，WANG Zhaocheng，et al. Improved DFT-based channel estimation for OFDM systems over multipath channels[C]//Proc. 6th International Wireless Communications and Mobile Computing Conference.[S.l.]：ACM Press，2010：585-590.

[8] 李世平，李鑫. 基于DFT判决门限的 OFDM 信道估计算法[J].计算机应用，2011，31(12)：3230-3232.

[9] 宋水正，何春，田丹，等. OFDM中基于导频的加窗FFT信道估计[J]. 通信技术，2011，44(2)：19-21.

[10]杨晋生，熊积慧. 引入阈值和判决指导的DFT信道估计算法[J]. 系统工程与电子技术，2012，34(2)：375-37.

DFT Channel Estimation Algorithm Based on Improved Threshold

WU Junqin, HUANG Qianqian

(SchoolofInformationEngineering,JiangxiUniversityofScienceandTechnology,JiangxiGanzhou341000,China)

In the OFDM system, DFT-based channel estimation algorithm do not suppress the noise within the cyclic prefix. Aiming at this issue, setting the threshold in time domain could effectively suppress the noise. Considering the deficiencies of threshold algorithms mentioned by other literatures, a new threshold algorithm is proposed. It takes the average energy of the middle part of the sample points after ascending multiplied by the appropriate factor, as the new threshold. Simulation results show that the improved algorithm can further suppress the noise, and improve the performance greatly with small increase of computational complexity.

OFDM; channel estimation; DFT; cyclic prefix; threshold

国家自然科学基金项目(11062002)；江西省科技厅青年基金项目(20142BAB217002)；江西省教育厅青年基金科技项目(GJJ13387)

TN911.23

A

10.16280/j.videoe.2015.17.021

2015-03-07

【本文献信息】吴君钦,黄茜茜.基于阈值改进的DFT信道估计算法[J].电视技术,2015，39(17).

吴君钦(1966— )，副教授，硕士，主要研究方向为嵌入式计算机系统设计及应用、宽带通信、信号与信息处理；

黄茜茜(1990— )，女，硕士生，主研移动通信。

责任编辑：许 盈