基于角点检测和NMF的图像Hash算法
2015-05-05张荣华柳忠彬廖红华杨大志
张荣华,柳忠彬,廖红华,杨大志
(1.四川理工学院 机械工程学院,四川 自贡 643000;2.湖北民族学院 信息工程学院,湖北 恩施 445000)
基于角点检测和NMF的图像Hash算法
张荣华1,柳忠彬1,廖红华2,杨大志1
(1.四川理工学院 机械工程学院,四川 自贡 643000;2.湖北民族学院 信息工程学院,湖北 恩施 445000)
为了有效地实现图像Hash函数在图像认证检索中的应用,提出了结合Harris角点检测和非负矩阵分解(NMF)的图像Hash算法,首先提取图像中的角点,对角点周围图像块信息进行非负矩阵分解得到表征图像局部特征的系数矩阵,进一步量化编码产生图像Hash。实验结果表明,得到的图像Hash对视觉可接受的操作如图像缩放、高斯低通滤波和JPEG压缩具有良好的稳健性,同时能区分出对图像大幅度扰动或修改的操作。
图像认证检索;Harris角点检测;非负矩阵分解(NMF);图像Hash
鉴于数字媒体传播的广泛性和交互性,对其内容的防伪、篡改、完整性认证等问题越来越引起用户的关注,尤其是数字图像已成为最重要的媒体信息之一,如何有效地实现图像的管理、认证及检索已成为亟待解决的问题。针对这一现象,本文研究稳健图像摘要[1]或哈希(Hash)算法,即通过分析提取图像的颜色、形状、纹理、空间关系等特征并进一步编码,用一个较短的固定长度的数字序列标识该图像。图像摘要在完整性认证、图像检索、数字水印等方面有广泛的应用前景。
目前,图像Hash算法大致可分为4大类[2]。基于空间统计特性[3-4],文献[4]中先对图像进行小波分解,接着把每个频带随机分块,对每个块统计量化构造哈希序列,该算法对JPEG压缩、几何失真有较好的稳健性;基于变换域系数相关性,Lefebvre[5]等用Radon变换构造图像Hash,该方法对基本图像攻击如压缩、滤波、模糊等稳定性较好;基于粗略特征描述,Fridrich[6]等指出图像在发生显著变化后,其DCT低频系数也会改变,由此提出将图像DCT系数矩阵投影到随机平滑模板上,计算每块投影的内积,并将其量化映射成固定长度的数字序列,进而得到图像哈希,该摘要算法对一般图像攻击有较好的鲁棒性,但对几何变换效果不佳;基于视觉特性,在计算图像Hash时引入人眼视觉特性(Human Visual System,HVS)[7-8],使图像Hash能更好地反映图像视觉特征,文献[8]中增大人眼敏感的频域系数在计算图像Hash时的权重,首先将原始图像的分块DCT系数乘以由密钥控制生成的伪随机矩阵,接着进行基于分块的Watson人眼视觉特性处理,最后进行量化以产生图像Hash,该算法提高了对JPEG压缩和高斯滤波的鲁棒性。近年来,也出现了融合多种图像特征提取方法来构建图像Hash的方法,文献[9]中提出了结合尺度不变特征变换(SIFT)和主成分分析(PCA)的感知哈希方法,对图像旋转、光照变化、图像滤波等攻击具有一定的稳健性。
基于以上分析,提出一种采用Harris角点检测结合非负矩阵分解,提取特征点周围图像信息的摘要算法。该方法考虑到图像中边缘、角点、斑点、直线段、圆等基元包含了图像的特征信息,而其中图像角点的局部具有较好的稳健性,实验结果表明,该方法具有较好的视觉稳定性和区分内容不同图像的能力。
1 Harris角点检测原理
角点是两个边缘的连接点,图像梯度有很大的变化,Harris角点检测[10]使用特征点来描述图像的内容。设计一个局部窗口(高斯函数)沿图像各方向移动,窗口的平均能量会发生明显改变,即图像局部曲率突变,当能量改变值大于设定的阈值时,则选取该窗口的中心像素点为角点。
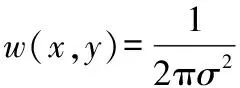
(1)
为了寻找包含角点的窗口,则需要找出像素灰度变化较大的窗口,即
max[I(x+u,y+v)-I(x,y)]2
(2)
使用泰勒展开得
(3)
式中:Ix,Iy表示图像一阶灰度梯度。

2 非负矩阵分解
非负矩阵分解(Nonnegative Matrix Factorization,NMF)[11],是当矩阵中全部元素均为非负数时的一种矩阵分解方法,适合图像的非负性质,有助于处理大规模数据,占用存储空间少,矩阵分解得到的低秩可大大降低矩阵维数。
对于非负矩阵V,存在W≥0,U≥0,满足:Vn×m≈Wn×r·Ur×m,其中r为特征维数,nm>(n+m)r,即将一个非负的矩阵分解为两个非负矩阵相乘,W称为基矩阵,U称为系数(权重)矩阵,这种基于基向量组合的表示形式反映了人类思维中“局部构成整体”的概念。
定义目标函数来描述V≈WU的近似效果,用分解前后两个非负矩阵V和WU之间的距离来度量。第一种方法为欧氏距离,即
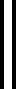
(4)
第二种方法是利用V与WU间的广义K-L散度,即
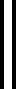
(5)
由此,NMF的问题就转化为使目标函数最小化的优化问题,可以通过迭代运算求解,为保证非负矩阵分解结果的非负性,采用文献[12]提出的K-L散度下迭代法则
(6)
(7)
随机初始化W和U,通过50~100次迭代运算得到分解结果。
3 图像Hash算法
密码学中代表性的Hash算法有MD5和SHA-1,目的是找到数据内容和存放地址之间的映射关系,其对输入数据的变化很敏感,这样的摘要算法并不适用于图像。因为在实际应用中常需要对图像进行如滤波、压缩、增强、加噪、缩放等多种操作,并未改变图像特征,此时哈希序列应保持不变。另一方面,如果图像内容被大幅度修改后,应使哈希序列完全改变,才能实现防伪认证的目的。设图像为I,H(I)为哈希函数,h=H(I)即为提取对象I得到的Hash值,由此图像Hash应具备以下特点:


3.1 Hash提取
Hash提取算法的流程图如图1所示。

图1 Hash提取流程图
具体步骤描述如下:
1)预处理:Harris角点检测算法对图像的缩放敏感,因此,采用双三次插值将输入图像规格化到统一大小512×512,减少图像缩放操作对Harris角点位置的影响。
2)对图像进行Harris角点检测。
3)Harris角点检测得到的是像素点,以该点为中心,设定g×g大小的窗口,对边缘点窗口大小可能不足g×g,再次双三次插值规格化为g×g窗口大小。
4)对包含角点的窗口图像块信息,进行非负矩阵分解。
5)生成特征向量:经过NMF后得到系数(权重)矩阵Ur×g,它表征了图像的局部特征,对U矩阵计算每一列均值x(i), 并把每一个元素与均值进行比较,得到矩阵Cr×g,其中
(8)
(9)
6)生成Hash序列:将g个特征向量转化为二进制序列,生成图像Hash序列。
3.2 相似性度量
采用归一化Hamming(汉明)距离表征图像的相似程度,即
(10)
式中:L为Hash序列的长度;H(I1),H(I2)分别为图像I1,I2提取的哈希序列。
归一化Hamming距离具有以下特性:图像内容之间越相似,归一化Hamming距离越趋近于0;当图像之间不相似的程度逐渐增大时,归一化Hamming距离也随之增大;当感知两个内容不相关的图像时,归一化Hamming距离的期望值越趋向于0.5。
4 实验结果
4.1 鲁棒性分析
采用常见的视觉可接受的保持图像内容不变的操作来测试图像Hash算法的鲁棒性。选取大小为512×512的标准图像Lena,Boat,Tank,Airplane和House进行实验,分别对其进行缩放变换,高斯低通滤波和JPEG压缩处理,计算操作前后图像哈希间的Hamming距离,结果如图2~4所示。图中纵坐标为原标准图像与受攻击后图像的归一化Hamming距离,横坐标分别表示缩放比例,高斯滤波3×3掩模的标准差σ,JPEG压缩质量因子。图2说明了哈希序列受图像缩放变换影响的情况,当缩放比例小于1时,图像质量下降,此时Hamming距离有较为明显的增大趋势,而缩放比例大于1时,则对哈希序列的影响较小;图3表明随着标准差σ增大,Hamming距离也相应增大;图4表明随着JPEG压缩质量因子增大,Hamming距离下降。从图2~图4可以看出,该图像Hash方法对适度的图像缩放、高斯低通滤波、JPEG压缩具有鲁棒性。

图2 图像缩放

图3 高斯低通滤波

图4 JPEG压缩
4.2 区分性分析
根据图像Hash的区分性(抗碰撞性)条件,图像Hash算法除需对保持图像内容不变的操作具有良好的鲁棒性外,还需能够区分两幅内容不同或者被恶意篡改过的图像,即此时哈希序列值也应有较大差别。选取大小为512×512的标准图像Lena,Boat,Tank,Airplane,House,Pepper和Splash进行实验,如表1所示,不同图像间的汉明距离均较大,各标准测试图像间归一化汉明距离最大为0.827 3,最小为0.292 8,说明该哈希算法足以区分不同图像,满足抗碰撞性,对图像大幅度扰动等攻击敏感。
表1 标准测试图像间的归一化Hamming距离

测试图像LenaBoatTankAirplaneHousePepperSplashLena0036610513704099047620453006798Boat0366100407802982036290562107550Tank0513704078003595029280678208273Airplane0409902982035950032140594807801House0476203629029280321400651108118Pepper0453005621067820594806511005095Splash0679807550082730780108118050950
4.3 性能对比
为了测试算法的分类性能,从华盛顿大学的CBIR图像库选取100幅图像,分别对其进行缩放变换,高斯低通滤波和JPEG压缩处理,即每一幅图都生成相似图像,采用接收者操作特征曲线(Receiver Operating Characteristic Curve,ROC),与文献[13]基于NMF哈希方法对比,测试算法的分类性能,为此计算两种方法的真正率TPR和假正率FPR
TPR=TP/(TP+FN)
(11)
FPR=FP/(FP+TN)
(12)
式中:TP(真正)表示被预测为相同图像的相似样本;FN(假负)表示被预测为不同图像的相似样本,则把所有实际为相似图像的样本,正确地判断为相似图像的比率称为TPR;FP(假正)表示被预测为相似图像的不同样本;TN(真负)表示被预测为不同图像的不同样本,则把所有实际为不同图像的样本,错误地判断为相似图像的比率称为FPR。ROC曲线从全局上反映算法的鲁棒性和区分性,越靠近左上角的曲线算法性能越好。从图5可以看出,基于角点检测和NMF的图像哈希算法优于文献[13]。

图5 本文哈希算法与文献[13]算法ROC曲线
5 小结
提出了一种稳健图像Hash算法。从图像中提取的Harris角点对于视觉可接受的操作具有良好的抗干扰性,对以角点为中心g×g大小的窗口,应用非负矩阵分解实现数据压缩降维,而且图像的主要内容特征能通过系数矩阵提取出来,进一步对系数矩阵进行量化编码实现了图像与一个二进制序列的映射。实验结果表明,该算法具有抵御图像缩放、高斯低通滤波、JPEG压缩攻击的稳健性,能区分不同图像,具有对图像恶意扰动或篡改等攻击的敏感性。进一步的研究将提取图像中对视觉特性更稳健的特征点,引入密钥,以进一步提高Hash性能。
[1] 牛夏牧,焦玉华.感知哈希综述[J]. 电子学报,2008,36(7):1405-1411.
[2] 叶卫国,韩水华.基于内容的图像Hash算法及其性能评估[J].东南大学学报:自然科学版,2007,37(Z1): 109-113.
[3] 王玮.基于小波域滤波的迭代硬阈值压缩感知重构[J].电视技术,2014,38(9):32-35.
[4] VENKATESAN R, KOON S M, JAKUBOWSKI M H,et al. Robust image hashing[C]//Proc. IEEE International Conference on Image Processing.Vancouver BC,Canada:IEEE Press,2000:664-666.
[5] LEFEBVRE F,MACQ B,LEGAT J D. RASH:Radon soft hash algorithm[C]//Proc. European Signal Processing Conference. Toulouse,France:IEEE Press,2002:299-302.
[6] FRIDRICH J, GOLJAN M. Robust hash functions for digital watermarking[C]//Proc. IEEE International Conference on Information Technology:Coding and Computing. LasVegas,Nevada,USA:IEEE Press,2000:178-183.
[7] 张慧, 张海滨,李琼,等.基于人类视觉系统的图像感知哈希算法[J]. 电子学报,2008,36(12A):30-34.
[8] 秦川,王朔中,张新鹏.一种基于视觉特性的图像摘要算法[J].中国图象图形学报,2006,11(11):1678-1681.
[9] 孙锐,闫晓星,高隽.基于SIFT和PCA的图像感知哈希方法[J]. 电路与系统学报,2013,18(1):274-278.
[10] HARRIS C,STEPHENS M. A combined corner and edge detector[C]//Proc. Alvey Vision Conference.[S.l.]:IEEE Press,1988:147-151.
[11] LEE D D,SEUNG H S. Learning the parts of objects by nonnegative matrix factorization[J]. Nature,1999(21):788-791.
[12] LEE D D,SEUNG H S. Algorithms for non-negative matrix factorization[C]//Proc. Advances in Neural Information Processing Systems.[S.l.]:IEEE Press,2001:556-562.
[13] MONGA V,MIHÇAK M K. Robust and secure image hashing via non-negative matrix factorizations[J].IEEE Trans. Information Forensics and Security,2007,2(3):376-390.
张荣华(1987— ),女,硕士,研究方向为图像处理、机器视觉;
柳忠彬(1972— ),教授,硕士生导师,研究方向为机械设计、逆向工程、仿真分析;
廖红华(1972— ),博士,副教授,硕士生导师,研究方向为图像处理、嵌入式系统;
杨大志(1976— ),副教授,研究方向为嵌入式系统、信息获取及处理。
责任编辑:时 雯
Image Hashing Based on Harris Corners and NMF
ZHANG Ronghua1,LIU Zhongbin1,LIAO Honghua2,YANG Dazhi1
(1.SchoolofMechanicalEngineering,SichuanUniversityofScience&Engineering,SichuanZigong643000,China; 2.SchoolofInformationEngineering,HubeiUniversityforNationalities,HubeiEnshi445000,China)
In order to apply the image Hash in image authentication and retrieval effectively,a new image Hashing algorithm based on Harris corners and nonnegative matrix factorization (NMF) is proposed,firstly Harris corners are identified,around the Harris corners of image block information runs NMF to obtain the coefficient matrix that capture the local features of image. Then,these features are quantized and coded to generate the Hash vector. Test results indicate that the proposed method is robust against acceptable visual image scaling, Gaussian low-pass filtering and JPEG compression,at the same time is sensitive to image excessive changes or malicious tampering.
image authentication and retrieval;Harris corners detection;nonnegative matrix factorization(NMF); image Hash
国家自然科学基金项目(61263030)
TN911.73
A
10.16280/j.videoe.2015.17.008
2015-01-15
【本文献信息】张荣华,柳忠彬,廖红华,等.基于角点检测和NMF的图像Hash算法[J].电视技术,2015,39(17).
