基于BP神经网络的大学生深度学习水平预测模型构建
2015-05-05杜树杰
尹 桐,杜树杰
(中国海洋大学基础教学中心,山东青岛 266000)
基于BP神经网络的大学生深度学习水平预测模型构建
尹 桐,杜树杰
(中国海洋大学基础教学中心,山东青岛 266000)
由于BP神经网络强大的自组织和自适应能力,本文基于BP神经网络构建了大学生深度学习水平预测模型,使用NSSE-China2013问卷作为数据的来源,将院校间的五大可比指标作为网络的输入、大学生深度学习水平作为网络的输出,并在Matlab中仿真实现。实验结果表明,该预测模型克服了传统评价深度学习水平的复杂性和主观性,具有收敛速度快和预测精度高等特点,具有很好的适用性。
BP神经网络;大学生深度学习水平;NSSE-China;预测模型
随着国家逐渐步入学习型社会,国家和社会对于知识和人才的需求和重视程度逐渐加大,而大学生作为接受高等教育的精英群体,其学习情况直接影响着学习型社会的深度和广度,因此研究大学生的学习情况越来越具有现实意义。而评价学生的学习情况,不仅要衡量知识的广度和数量,还要考察学生是否善于将新思想与原有的知识结构相联系,并最终获得解决问题的能力,即深度学习能力。全球信息化的快速发展极大地改变了当代大学生的学习模式,大量的学生长期处于浅层学习当中,这会大大限制学校对学生解决问题能力和创新能力的培养。本文通过分析与预测大学生深度学习水平,可以帮助学生及时调整自身学习状态,帮助教师更加有针对性地改进教学策略,同时也可以为院校的教育改革提供科学的指导。
BP神经网络是一种人工智能算法,具有很强大的非线性映射能力、自组织和自适应能力。因此本文以中国海洋大学“大学生学习性投入调查”问卷(NSSE-China)所统计的数据作为依据,构建了评价大学生深度学习水平的数学模型,从而为大学生深度学习水平的研究提供一定的参考价值。
一、深度学习的内涵
深度学习和浅层学习这两个概念是由国外学者FerenceMarton和Roger Saljo在1976年联名发表的 《学习的本质区别:结果和过程》一文中首次提出的。[1]他们通过一项实验,总结出学生学习的两种不同学习策略,即浅层学习策略和深层学习策略。他们认为所谓浅层学习,就是指不加以思考地记住书本中提到的一些原理或事实,所关注的是在测验中遇到的书本中提及的那些内容;而深层学习,是指理解整本书中的思想,试图领会其学术内涵,关注的焦点是如何将书本中的知识应用在现实生活中。
经过长期对深度学习的深入研究,国内学者何玲和黎加厚在《促进学生深度学习》一文中对深度学习做出了较为精准的定义。所谓深度学习,是指在理解学习的基础上,学习者能够批判性地学习新的思想和事实,并将它们融入原有的认知结构中,能够在众多思想间进行联系,并能够将已有的知识迁移到新的情境中,做出决策和解决问题的学习。[2]
根据上述对深度学习的定义,可以将深度学习按照布鲁姆的教育目标分类学来对其进行概括和总结。布鲁姆等人在认知学习领域将教育目标分为六大类,从低级到高级依次为识记、理解、应用、分析、综合和评价。浅层学习的认知水平停留在第一、第二层,而深层学习的认知水平对应着后面的四层。[3]因此,本文认为深度学习是指批判性地接受新知识,通过整合原有知识,构建出属于自己的知识体系,并获得解决问题的能力。
本文的重点研究对象是大学生群体,相较于中学生群体而言,大学生群体拥有更多的自主学习时间和更为丰富的课余活动,获得教学资源的内容和途径也更加广泛和便捷,因此大学生的学习模式更多的是自主学习模式,这也是其与中学生的重要差别之一,大学生真正成为了学习活动的主体。同时,由于大学生即将离开校园步入社会,这一角色特殊性决定了大学教育应该更加注重培养学生创新和解决问题的能力,即深度学习能力。然而目前的研究发现,大量的大学生长期处于浅层学习状态,长此以往将不利于社会的进步,因此大学生深度学习能力的培养具有更大的研究价值。
二、构建预测模型
本文所采用的数据来源于2013年中国海洋大学“全美大学生学习型投入调查”汉化版(NSSE-China)问卷,通过筛选题目构成深度学习量表,来考查大学生深度学习水平的相关影响因素并构建预测模型。NSSEChina问卷的原型是印第安纳大学开发的 “全美大学生学习性投入调查”(National Survey of Student Engagement,以下简称NSSE)问卷。NSSE是一个针对美国全国范围内四年制本科院校学生投入高层次学习活动和发展程度的年度调查。[5]NSSE-China项目于2007年启动,经过一系列文化适应和预测试后于2009年首次在中国全国范围施测。[6]该问卷具体测量了几项指标,包括院校间的五大可比指标(具体包括学业挑战度LAC、主动合作学习水平ACL、生师互动SFI、教育经验的丰富程度EEE和校园环境的支持度SCE)、院校诊断九项指标、深度学习(DL)指标以及社会称许性指标。经清华大学的几次修订,目前的量表具有良好的信度与效度。[7]
本文利用NSSE-China问卷采集的数据来构建大学生深度学习水平预测模型。经过研究发现人工神经网络是构建预测模型非常有效的方法。其中BP神经网络是人工神经网络中应用最广泛的一种,其具有强大的非线性映射能力和自组织、自适应能力,因此本文选择利用BP神经网络来构建大学生深度学习水平预测模型。
将回收的有效问卷通过SPSS软件计算出每个学生的五大可比指标成绩与深度学习指标成绩。经分析数据得出,学生的深度学习指标成绩分布区间为9.09~100,本文将深度学习水平分为优秀、良好和不合格三个等级。分级标准如表1所示:
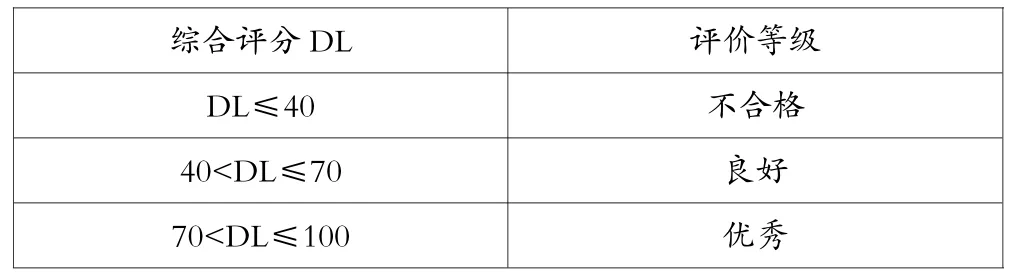
表1

BP神经网络是一种多层前馈神经网络。最基本的BP神经网络由输入层、隐含层和输出层组成,每层有许多互相不连接的神经元节点,相邻两层节点通过连接权连接,其拓扑结构如图1所示。
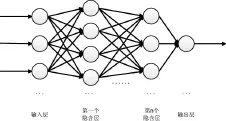
图1 BP神经网络结构
(1)输入层节点的确定
由于问卷当中涉及的院校间可比指标有5个,因此,输入层神经元个数定为n=5。其中:X1表示学业挑战度,学业挑战度的考察包含了学生个体和院校组织两个层面的含义——既要反映学生的学习行为表现及其在学业上的时间和精力的投入程度,又要通过学生的行为表现和自我报告来间接对高校的学业要求、学业标准和对学业的支持程度等进行评价,以体现高校的教育质量。[8]X2表示主动合作学习水平,评价的是学生的合作性学习能力和与多元人群讨论的能力。X3表示生师互动,评价的是学生与教师互动的频繁程度及其主动性和互动的质量。X4表示教育经验的丰富程度,评价的是教师教学实践的有效性,包括有组织的教学活动、清晰的知识讲解、具有说明性的举例和有效的反馈。X5表示校园环境的支持度,评价的是校园中人际沟通的质量和学校对促进学生学习和发展的支持程度。
(2)输出层节点的确定
本文主要是来评价大学生的深度学习情况,最终目的是能够得到一个客观、准确地反映大学生深度学习水平的量化值。因此本文将大学生深度学习水平的量化值作为BP神经网络的输出向量,即输出层神经元个数确定为m=1。
(3)隐含层个数的确定
如今尚不存在一个确定的标准来计算隐含层的神经元个数,但可以根据以下公式来计算出隐含层神经元数量的大概区间范围,进而通过试凑的方法来确定最佳的隐含层的神经元个数。因为输入层神经元个数为5,输出层神经元个数为1,则在参考经验公式l〈n-1,l〈(式中,n为输入层节点数;l为隐含层节点数;m为输出层节点数;a为0-10之间的常数)的基础上,初步选取一个比较小的隐含层节点数进行训练,如果达到了规定的训练次数或者在有限的训练次数内没有收敛,则停止训练,然后逐步增加隐含层节点数,重新训练。综合分析多次训练效果,最终确定该网络的隐含层个数为两个,且每个隐含层的个数分别为25和20。

为取消各维数据间数量级差别,避免因为输入输出数据数量级差别较大而造成的网络预测误差较大,神经网络一般会对数据进行归一化处理。本文采用公式为的函数对数据进行归一化,并将数据处理为在区间[0,1]之间的数据。

传递函数的选择与输入数据和输出数据的取值区间有关,经过多次实验,观察网络的训练效果,最终将第一个隐含层的传递函数参数确定为S型正切函数,第二个隐含层的传递函数参数确定为S型对数函数,输出层的传递函数确定为线性函数。其对应的函数数学表达式依次如下:
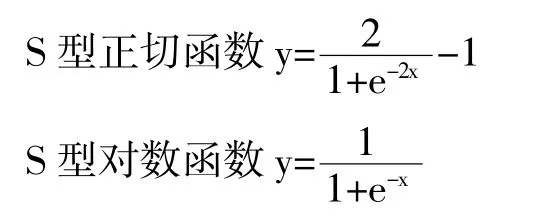
线性函数y=x
通过观察多次训练效果,发现本网络模型的收敛速度快、训练时间短且训练效果良好,因此该网络选取BP网络标准的最速下降法作为训练的方法即可。其他函数参数均选用BP神经网络工具箱的默认值。
根据网络的性能来设定网络的训练参数。其中将网络的最大训练次数设置为100次,如果超过该次数网络仍然没有收敛则表示网络不收敛,训练停止;将网络的最大确认失败次数设置为15次,即网络的验证误差连续15次没有下降,则表明网络的训练效果不好,训练停止;将网络的训练目标设置为0.003,当网络的目标误差达到该目标值时,训练停止。
三、Matlab仿真实现
BP神经网络模型主要借助Matlab语言工具来实现。

根据上述构建的网络预测模型和函数参数的设置,对网络进行训练,具体训练过程如下:
(1)将训练数据进行归一化处理,使其分布在[0,1]之间,并将预测输入数据按照同样的归一化方式进行归一化处理。
(2)将归一化后的数据输入到网络模型当中,按BP网络的学习算法训练网络,其流程图如图2所示,最后将预测输出进行反归一化处理。
(3)将预测输出和期望输出按照分数区间划分为三大类,即优秀、良好和不合格,并计算该网络模型的准确率。
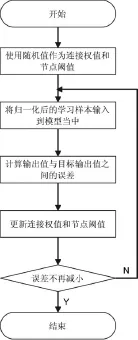
图2 BP学习算法流程
(4)画出BP网络预测输出图形和神经网络预测误差百分比图形

BP神经网络的学习属于有监督式的学习,需要一组已知目标输出的学习样本集。因此本文从2013年中国海洋大学NSSE-China问卷中挑选出预测模型所需的1000组数据,并随机抽取其中的900组数据作为训练样本,其余100组数据作为检验样本,输入到网络模型当中,得到如图3所示的BP神经网络学习训练过程曲线。从图中可以看出,训练迭代次数达到5次时,网络已经收敛并且网络的预测精度达到了设定的目标值。训练达到要求后,选取100组作为检验样本,经上述网络模型输出的结果与调查问卷中所显示的大学生深度学习水平评价等级的结果相比较具有一致性,其预测输出与期望输出的相对误差较小。举例如表2所示,由于用于测试网络准确度的检验样本较多,表2中只列举了从检验样本中随机挑选的10组数据进行比较。
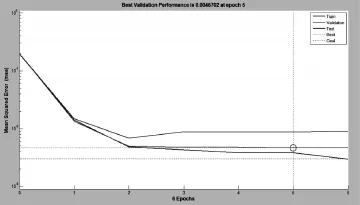
图3 BP神经网络学习训练过程
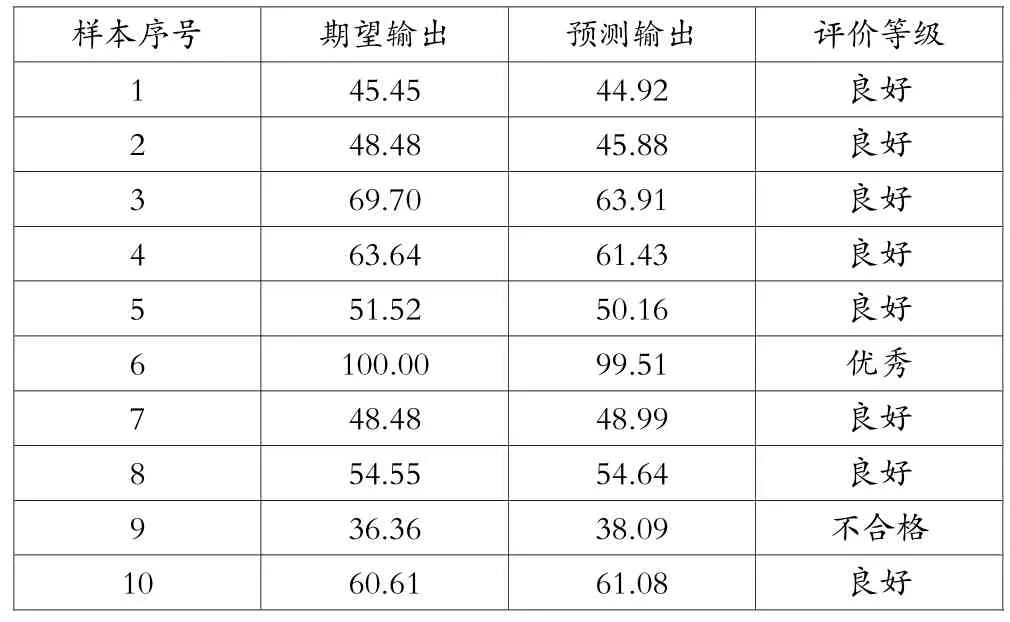
表2
100组检验样本的BP网络预测输出如图4所示,神经网络预测误差百分比如图5所示。从这两幅图中可以看出,在100组检验样本中有88组样本的预测输出值与其期望输出值相符,预测准确率高达88%,总体预测误差严格控制在20%之内。因此证明本文所构建的大学生深度学习水平预测模型具有很高的预测精确度。
本文为了检验预测输出对期望输出的拟合程度,在BP网络训练完成后的处理过程中对预测输出的结果进行了回归分析,回归直线方程式为:y=0.18x+0.13,相关系数R=0.897,通常情况下相关系数R越接近1表明网络的拟合程度越好,所以根据回归分析说明该模型的预测输出有效。
由于该网络的输入和输出值是随机选取的,因此每次训练的结果均有一定程度的差异,本文对网络进行了10次训练,计算出的平均准确率为85.3%。可以表明该网络的准确度比较理想,能够根据院校间的五大可比指标来预测大学生的深度学习水平,具有一定的应用价值。
四、结论
BP神经网络具有“相似形输入,相似形输出”的特征,所以该方法的预测精度和科学性不仅取决于训练样本的数量,更取决于训练样本的质量。[9]训练样本的数量越多,质量越高,越能精确地预测出大学生的深度学习水平。同时,BP神经网络具有很强的自组织和自适应性,因此利用BP神经网络算法来构建大学生深度学习水平预测模型,可以使其预测结果更加精准且富有合理性。

图4 BP网络预测输出

图5 神经网络预测误差百分比
本文构建的大学生深度学习水平预测模型,具有预测精度高、学习速度快等特点。通过此预测模型,既可以使大学生及时地掌握自身的学习情况,也可以使教师更加方便地评价本班学生的学习状况并有针对性地改善自己的教学策略,同时,也可以为学校的教学改革提供科学性的指导。因此利用BP神经网络算法构建的大学生深度学习水平预测模型,在学习分析和教育改革领域具有一定的实用价值和广泛的使用前景。
[1]Marton F.and SljR.On Qualitative differences in learning-Outcome and Process[J].British Journal of Edu-cational Psychology 1976(46):4-11.
[2]何玲,黎加厚.促进学生深度学习[J].计算机教与学,2005(5):29-30.
[3]王珏.杜威的教育思想与深度学习[J].教育技术导刊,2005(9):6-8.
[4]唐吉洪,张秀琦,程琳.基于BP神经网络的教师教育技术能力培训评价[J].计算机技术与发展,2013(6):249-252.
[5]张文毅,李汉邦.NSSE对我国本科教学工作评估的启示[J].中国高教研究,2009(10):19-22.
[6]ROSS H,CEN,Y.Reinterpreting quality through assessingstudentengagementin china[G].//SOLOMONIDES I,PETOCZ P,REID A(Eds.).Engaging with Learning in Higher Education.Faringdon,Oxfordshire:Libri,2012: 383-411.
[7]清华大学“全国大学生学习与发展追踪研究”课题.NSSE-China 2013问卷使用手册[Z].2013.
[8]吴凡.中美研究型大学本科生学业挑战度的比较研究[J].中国大学教学,2012(10):92-96.
[9]乔维德.基于BP神经网络的现代远程教育教学质量评价模型的构建[J].中国远程教育,2006(7):69-71.
(编辑:王天鹏)
G434
1673-8454(2015)23-0072-04
