红外成像导引头随动系统建模与仿真研究*

李鹏程，杨锁昌，李宝晨，岳智革

(军械工程学院 导弹工程系，河北 石家庄 050003)

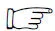
红外成像导引头随动系统建模与仿真研究*

李鹏程，杨锁昌，李宝晨，岳智革

(军械工程学院 导弹工程系，河北 石家庄 050003)

红外成像导引头是精确制导导弹系统的重要组成部分，导引头随动控制系统的性能决定着导弹的跟踪精度水平。为了提高其控制系统的动态性能和跟踪精度，设计了一种比例因子自校正模糊PID控制器并引入到导引头控制回路中。结果表明，与传统PID控制器相比，模糊PID控制器明显提高系统的动、静态指标，同时系统具有较强的适应性和鲁棒性。

导引头随动系统；自校正模糊控制；PID控制

0 前言

随动系统是红外成像导引头的关键技术之一，它直接影响红外成像导引头的跟踪速度和跟踪精度[1-3]。高性能的随动系统是提高发现目标概率、识别目标和精确跟踪的关键，对提高红外成像导引头的性能具有重要意义[4-5]。

本文是对红外导引头的角跟踪回路进行建模，综合对红外导引头重要性能指标和导引头恶劣的工作环境的考虑，结合传统比例积分微分(proportional integral derivative,PID)控制器的优点和模糊控制的特点[6-8]，设计了一种比例因子自校正模糊PID控制器，使红外成像导引头跟踪回路具有良好的动态性能与跟踪精度。与传统PID控制进行仿真比较，观察在不同预定角情况和加干扰情况下系统的输出以及角跟踪误差。

1 红外成像导引头随动系统工作原理及数学模型

随动系统有3个工作状态：预定状态、稳定状态和跟踪状态。预定是为快速搜索目标，根据对目标的预测将导引头的光轴指向目标所在位置；稳定是为了隔离姿态扰动，使导引头光轴稳定在惯性空间某一位置，确保成像清晰；跟踪是根据目标位置误差驱动导引头的光轴跟踪目标，同时测量目标视线角速率。

角跟踪回路由测角装置和光轴稳定回路组成。稳定回路实现了导弹姿态扰动运动的隔离；测角装置测出了目标视线角与光轴的角偏差，并将其放大后送往稳定回路，使得光轴向减小角偏差的方向运动，实现角度的自动跟踪。图1为角跟踪回路的原理框图[9]。

图1 角跟踪回路原理框图Fig.1 Block diagram of the angle tracking loop

红外导引头模型包括：

测角装置：Kce-τs；

(1)

开环增益：Kq；

(2)

(3)

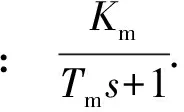
(4)

2 比例因子自校正模糊PID控制器设计

PID控制中一个关键的问题是参数的整定，传统的方法是在获取对象数学模型的基础上，根据某一整定原则来确定参数。但实际中，许多被控过程机理复杂，具有高度非线性、时变不确定性和纯滞后等特点；在噪声、负载扰动等的影响下，过程参数甚至模型结构均会随时间和工作环境的变化而变化，这就给PID控制器参数的确定带来了困难[10]。

PID参数模糊自整定是找出PID 3个参数与e和ec之间的模糊关系，在运行中通过不断检测e和ec，根据模糊控制原理来对3个参数进行在线修改，以满足不同e和ec时对控制参数的不同要求，而使被控对象具有良好的动、静态性能。比例因子自校正模糊PID控制器结构如图2所示[11]。

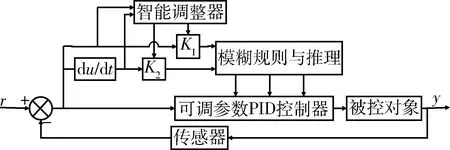
图2 比例因子自校正模糊PID控制器结构图Fig.2 Block diagram of Scaling factor self-tuning fuzzy PID controller

2.1 模糊PID控制器

2.1.1 模糊PID控制器算法

PID控制器的传递函数为

G(s)=KP+KIs+KDs，

(5)

式中：KP，KI及KD为比例、积分和微分增益。

PID参数的整定就是根据被控对象特性和所希望的控制性能要求来确定这3个参数[12]。用在线自整定的PID参数KP，KI，KD就可根据下列PID控制算法的离散差分公式计算输出控制u。

位置式PID控制算法表示为

u(k)=KPE(k)+KI∑E(k)+KD[E(k)-E(k-1)].

(6)

增量式PID控制算法表示为

Δu(k)=KP[E(k)-E(k-1)]+KIE(k)+

KD[E(k)-2E(k-1)+E(k-2)].

(7)

2.1.2 模糊化

模糊控制器有2个输入和3个输出，其中输入e为系统的角误差，论域范围为[-10,10]；输入ec为角误差的微分，论域范围为[-12,12]；3个输出分别为ΔKP,ΔKI及ΔKD，ΔKP，ΔKD的论域范围为[-3,3]；ΔKI的论域范围为[-0.06,0.06]。输入和输出变量的论域均划分为7个等级，即{-3,-2,-1,0,1,2,3}，其模糊集的语言变量取7个，为{NB,NM,NS,ZO,PS,PM,PB}，其含义依次为：负大，负中，负小，零，正小，正中，正大。

2.1.3 模糊规则

模糊推理的关键是模糊控制规则的确立。在设计模糊控制规则的过程中不但要考虑到误差的大小，而且还要考虑误差变化的情况，其原则是：当误差较大时，以尽快消除误差为主；而当误差较小时则要注意超调的发生，应以系统的稳定性为主要出发点。由前人的经验得知，被控过程对参数KP，KI，KD的自整定要求如下:

(1) 当偏差|e|较大时，需提高系统响应速度，应取较大的KP；为避免由于开始时偏差|e|的瞬时变大可能出现的微分过饱和而使控制作用超出许可的范围，应取较小的KD；同时为了防止系统响应出现较大的超调，产生积分饱和，应对积分作用加以限制，通常取KI=0，去掉积分作用。

(2) 当|e|和|ec|处于中等大小时，为使系统响应具有较小的超调，KP应取得小一些，KI的取值要适当，这种情况KD的取值对系统响应的影响较大，取值要大小适中，以保证系统响应速度。

(3) 当|e|较小即接近于设定值时，为使系统有良好的稳态性能，应增加KP和KI的取值，同时为避免系统在设定值附近出现振荡，并考虑系统的抗干扰性能，KD的取值是相当重要的，一般是当|ec|较小时，KD取大一些；当|ec|较大时，KD取小一些。

(4) 偏差变化量|ec|的大小表明偏差变化的速率，|ec|值越大，KP取值越小，KI取值越大。

根据以上原则，可得ΔKP，ΔKI及ΔKD的语言控制规则如表1-3所示。

表1 ΔKP模糊控制规则表Table 1 ΔKP fuzzy control rule table

表2 ΔKI模糊控制规则表Table 2 ΔKI fuzzy control rule table

2.1.4 反模糊化

由模糊推理得到的是一个模糊量,而最终需要的是输出一个精确的控制量。反模糊化就是实现由模糊量到精确量之间的转换。反模糊化的计算方法有很多种,最常见的有重心法、高度法和加权平均法。本系统采用工业控制中广泛使用的去模糊方法——重心法，即计算隶属度函数曲线包围区域的中心，其数学表达式为

(8)

式中:k为论域；u*为清晰化输出量；u为输出变量；μ为模糊集隶属函数。

2.2 比例因子参数自校正

对于一般二维模糊控制器，所描述的模糊控制器的控制规则关系是固定的，不可调整的。为了适应不同被控对象的要求，在原有基础上引进调整因子k1，k2，可得一种带有调整因子的控制规则：

U=-k1·e-k2·ec，k1,k2∈[0,1]，

(9)

式中：k1，k2为调整因子。通过调整k1，k2值，可以改变e和ec对控制输出量u的加权程度，从而调整了控制规则。

在实际控制中，对二维模糊控制系统来说，当偏差较大时，控制系统的任务是消除偏差，这时对偏差的加权k1应该大些；相反，当偏差较小时，此时系统接近稳态，控制系统的主要任务是使系统尽快稳定，为减小系统超调，这就要求在控制规则中偏差变化起的作用大些，即对偏差变化加权k2大些。因此，在不同的偏差范围时，考虑采用不同的加权因子，以实现控制规则的自调整。

3 仿真

用Simulink对红外成像导引头进行建模，并将比例因子自校正模糊PID控制器和传统PID控制器分别引入模型中进行仿真对比。

在系统输入预定角分别为1°，5°和10°的阶跃信号时，导引头角跟踪系统阶跃响应曲线见图3～5。从3个图中可看出PID和模糊PID的动态特性：超调量σ%，调节时间ts和上升时间tp，具体见表4。

在系统阶跃输入信号为5°时，导引头角跟踪跟踪误差曲线如图6，PID控制器的角跟踪误差为0.03°，而模糊PID控制器的角跟踪误差基本为0。在系统输入预定角为5°的阶跃信号，弹体正弦扰动幅值为3°，频率为3 Hz时，导弹控制系统的阶跃响应曲线如图7所示。弹体扰动条件下，PID控制器的预定误差为0.13°，模糊PID控制器的预定误差为0.02°

图3 预定角为1°时系统阶跃响应Fig.3 Step response of 1 ° predetermined angle

图4 预定角为5°时系统阶跃响应Fig.4 Step response of 5 ° predetermined angle

相比传统PID控制器，模糊PID控制能够实现系统的自适应调整，其响应曲线好，响应时间较短。同时，采用改进算法的系统阶跃响应的超调量小，稳态精度高，系统遇到干扰时能很快恢复稳态，动态性能好，并且具有良好的鲁棒性。

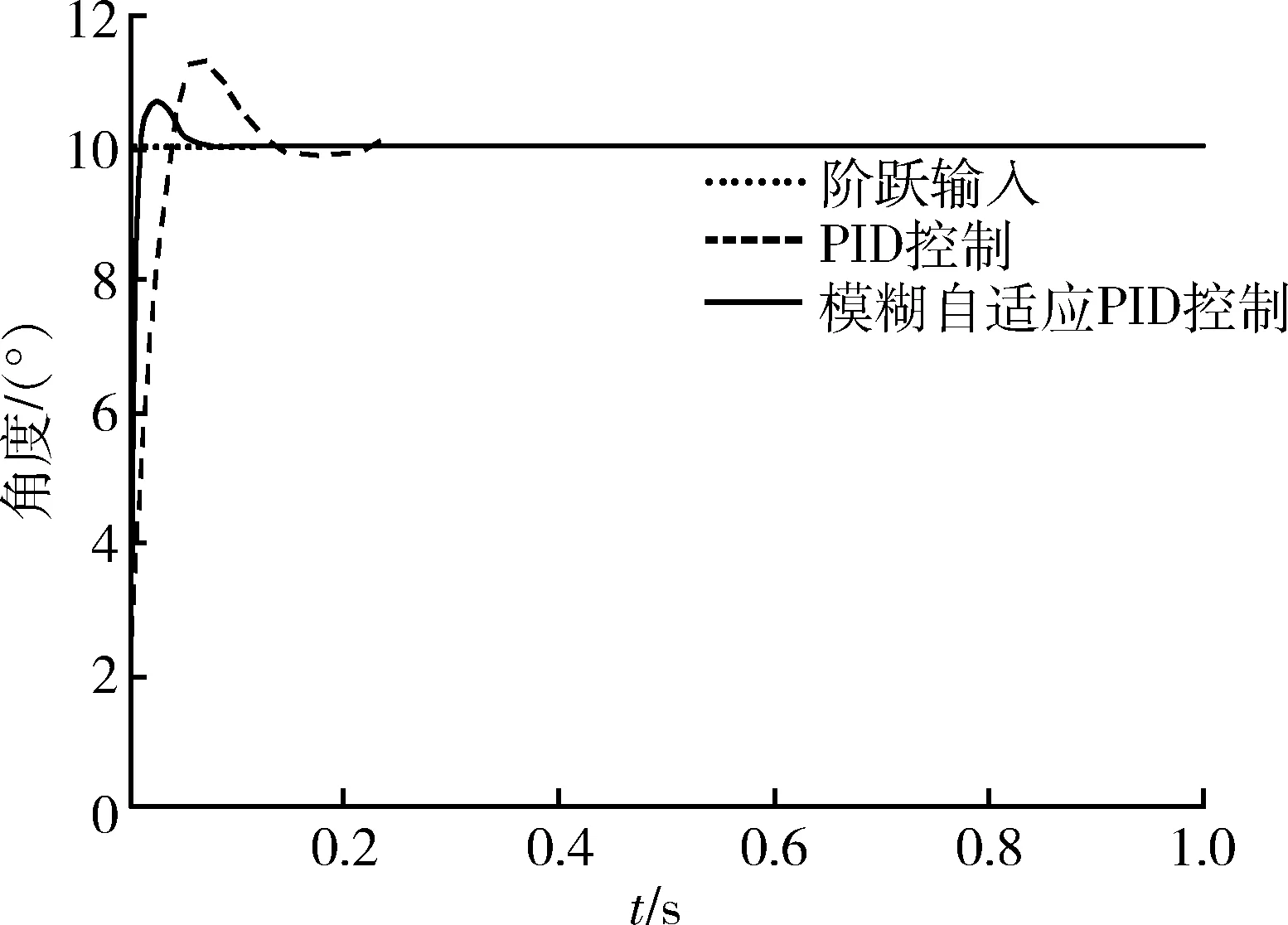
图5 预定角为10°时系统阶跃响应Fig.5 Step response of 10 ° predetermined angle

图6 预定角为5°时角跟踪误差Fig.6 Angle tracking error of 5° predetermined angle

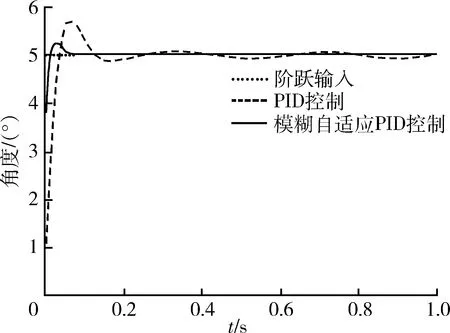
图7 正弦扰动幅值为3°频率为3 Hz时的阶跃响应Fig.7 Step response of sinusoidal perturbation amplitude of 3° 3 Hz frequency

表4 控制系统动态性能

Table 4 Control system dynamic performance

控制系统预定角/(°)1σ%ts/stp/s5σ%ts/stp/s10σ%ts/stp/sPID12．9950．24140．065012．9960．24220．064812．9950．24180．0651模糊PID9．1500．14070．01975．0550．14550．02656．7330．16320．0257

4 结论

比例因子自校正模糊PID控制器以传统PID控制器为基础，同时引入了加权因子和模糊控制方法，实现了控制规则的自调整和对PID控制中的3个参数的实时调整，其特点如下：

(1) 根据实际控制需要，及时调整加权因子以实现控制规则的自调整。

(2)KP，KI和KD3个参数根据系统偏差e和偏差的变化率ec动态变化，更符合控制当中的规律和特性。

(3) 控制精度高，反应时间短，与传统的PID控制相比，模糊PID控制器的超调量、振荡明显减少，瞬态时间缩短，且具有微小的静差。说明模糊PID控制指标优于传统PID控制。

此外，这种控制器的设计简单，控制规则修改灵活，控制算法修改以及编程灵活简单，易于模块化，且实时性好，并对被控对象具有很好的鲁棒性等设计上的优点。在红外导引头中使用，可以结合操作人员长期的经验积累，将这种经验作为模型化控制规则，配合以传统的PID随动系统，将可以有效提高红外系统的跟踪性能。

[1] 樊英平，王民钢，裴晓龙，等．红外成像导引头随动系统建模及仿真[J]．计算机仿真，2010，27(2)：76-79． FAN Ying-ping, WANG Min-gang, PEI Xiao-long, et al. Modeling and Simulation of Tracking System for IR Imaging Seeker [J]. Computer Simulation, 2010, 27(2): 76-79.

[2] TANG K S, Kim Fung Man, Guanrong Chen,et al. An Optimal Fuzzy PID Controller [C]∥IEEE Transactions On Industrial Electronics，2001，48(4)：757-765.

[3] KAZEMIAN H B,PhD. Intelligent Fuzzy PID Controller [J]. Mathematical Modeling: Theory and Applications, 2008,24:241-260.

[4] 黄春蓉,高翔,杨俊超，等.红外空空导弹导引头预定回路模糊PID双模控制研究[J].弹箭与制导学报,2010,30(2):10-14. HUANG Chun-rong, GAO Xiang, YANG Jun-chao, et al. Dual Fuzzy PID Control for Scan Loop of Infrared Guided Air-to-Air Missile Seeker [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(2): 10-14.

[5] 张向锋，李言俊．红外成像导引头模糊PD控制器设计与仿真[J]．弹箭与制导学报，2011，31(3)：35-37． ZHANG Xiang-feng, LI Yan-jun. Design and Simulation of Fuzzy PD Controller for Infrared Imaging Seeker [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(3): 35-37.

[6] 卢泽生,张强.高精度交流伺服系统的模糊PID双模控制[J].北京航空航天大学学报,2007,33(3):315-318. LU Ze-sheng, ZHANG Qiang. Fuzzy-PID Double Mode Control of Ultra-Precision AC Servo System [J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(3): 315-318.

[7] 张晓峰,杨军,祝小平.高精度电动舵机模糊自适应控制器设计[J].弹箭与制导学报,2010,30(1):30-32. ZHANG Xiao-feng, YANG Jun, ZHU Xiao-ping. Design of Fuzzy Adaptive Controller for High Precise Electromechanical Actuator [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(1): 30-32.

[8] 崇阳，李言俊，张科，等.基 于 FPGA的 模 糊 PID舵 机控 制 算 法 设 计 与 实 现[J].飞行力学，2011，29(2)：86-88. CHONG Yang, LI Yan-jun, ZHANG Ke, et al. Design and Implementation of Digital Fuzzy-PID Actuator Control System [J]. Flight Dynamics, 2011, 29(2): 86-88.

[9] 张义广，杨军，朱学平，等．非制冷红外成像导引头[M]．西安：西北工业大学出版社，2009． ZHANG Yi-guang, YANG Jun, ZHU Xue-ping, et al. Uncooled Imaging Infrared Seeker [M]. Xi’ an: Northwestern Polytechnical University Press, 2009.

[10] 耿峰，祝小平．精确制导武器红外成像导引头控制系统研究[J]．宇航学报，2007，28(3)：535-538． GENG Feng, ZHU Xiao-ping. The Research of Accuracy Guidance Weapon Infrared Imaging Seeker Control System [J]. Journal of Astronautics, 2007, 28(3): 535-538.

[11] 刘金琨．先进PID控制MATLAB仿真[M]．北京：电子工业出版社，2004． LIU Jin-kun. MATLAB Simulation of Advanced PID Control [M]. Beijing: Publishing House of Electronics Industry, 2004.

[12] 王涛，何玉珠．电视导引头伺服系统模糊PID控制技术研究[J]．测控技术，2011，30(6)：57-60． WANG Tao, HE Yu-zhu. Research on Fuzzy-PID Control Technique for Servo System of TV Seeker [J]. Measurement and Control Technology, 2011, 30(6): 57-60.

Fuzzy PID Control for Infrared Imaging Seeker Servo System

LI Peng-cheng,YANG Suo-chang,LI Bao-chen,YUE Zhi-ge

(Mechanical Engineering College,Department of Missilery Engineering,Hebei Shijiazhuang 050003, China)

Infrared imaging seeker is considered as one of the most important parts of the precision-guided missile, while the performance of the seeker control system is a vital prerequisite to improve the tracking accuracy. In order to improve the performance of system, a scale factor self-correction fuzzy proportional integral derivative (PID) controller is designed and introduced into the seeker control loop. The simulation results show that the fuzzy control system can improve the dynamic and static performance and strengthen the robustness and suitability of the system, compared to the traditional PID.

infrared imaging seeker; self-correction fuzzy control; proportional integral derivative(PID) control

2013-12-04；

2014-06-21

李鹏程(1989-)，男，河北石家庄人。硕士生，研究方向为导弹制导与控制。

通信地址：830006 新疆乌鲁木齐市沙依巴克区仓房沟东路473号 E-mail：lpccole@163.com

10.3969/j.issn.1009-086x.2015.03.015

TJ765.3+31；TP391.9

A

1009-086X(2015)-03-0083-06