法拉第电磁感应定律应用例析

付霞+张素荣+吕安延

法拉第电磁感应定律的应用是高考的热门考点，求解感应电动势则是解题的关键。在电磁感应现象中可以分为两类，一类是磁场变化产生感生电动势E感=■S，一类是导体在磁场中运动切割磁感线产生动生电动势E动=■B，常用E动=BLv求解。下面通过高考题进行分类例析。

一、感生电动势的求解

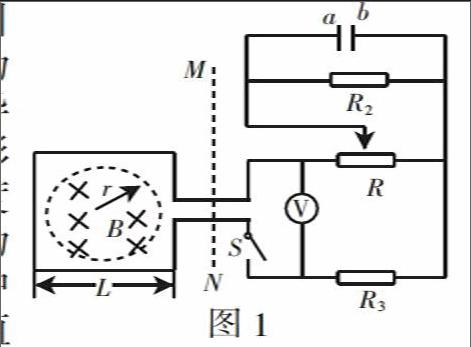
例1 （2013年四川高考）如图1所示，边长为L、不可形变的正方形导线框内有半径为r的圆形磁场区域，其磁感应强度B随时间t的变化关系为B=kt（常量k>0）。回路中滑动变阻器R的最大阻值为R0，滑动片P位于滑动变阻器中央，定值电阻R1=R0、R2=■。闭合开关S，电压表的示数为U，不考虑虚线MN右侧导体的感应电动势，则（ ）

A.R2两端的电压为■。

B.电容器的a极板带正电。

C.滑动变阻器R的热功率为电阻R2的5倍。

D.正方形导线框中的感应电动势为KL2。

解析：由法拉第电磁感应定律E=■=■S=kπr2，可知D错。R2与R是并联，并联滑动变阻器的阻值为■，并联后电阻为■，则滑动变阻器所在支路的电阻为■，外电路的总电阻为：R总=R1+■=■，故R2两端电压为：■U=■U，所以A正确；电路左侧正方形导体内磁场变化产生逆时针电流，导体框相当于一个上负下正的电源，所以电容器a极板带负电，故B错误；设干路电流为I，则通过滑动变阻器左半部分的电流为I，通过其右半部分的电流为■，由于此部分与R2并联且阻值相等，因此通过R2的电流也为■，由P=I2R知：滑动变阻器热功率为P=I2■+（■）2■=■，R2的热功率为：P2=（■）2■=■，所以滑动变阻器R的热功率为电阻R2的5倍，故C正确；由A的分析知D错。答案：AC。

点评：公式E感=■S中的面积须是存在磁场的有效面积。在内电路中电流从电源的负极流向正极，根据楞次定律判断感应电流的方向，四指所指的方向—线圈上端为电源的正极；再利用恒定直流电路中的相关规律和公式解题。

二、动生电动势的求解

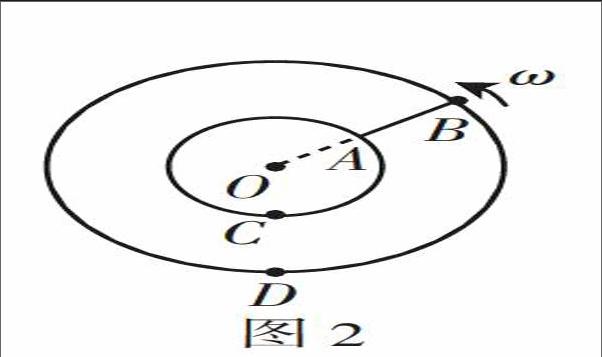
例2 （2014年全国课标Ⅱ）如图2所示，半径分别为r和2r的同心圆形导轨固定在同一水平面内，一长为r，质量为m且质量分布均匀的直导体棒AB置于圆导轨上面，BA的延长线通过圆导轨中心O，装置的俯视图如图所示。整个装置位于匀强磁场中，磁感应强度的大小为B，方向竖直向下，在内圆导轨的C点和外圆导轨的D点之间接有一阻值为R的电阻（图中未画出）。直导体棒在水平外力作用下以角速度ω绕O逆时针匀速转动，在转动过程中始终与导轨保持良好接触。设导体棒与导轨之间的动摩擦因数为μ，导体棒和导轨的电阻均可忽略。重力加速度大小为g。求：

（1）通过电阻R的感应电流的方向和大小；

（2）外力的功率。

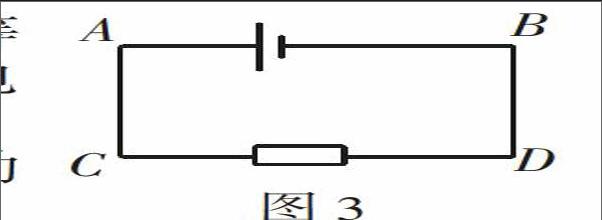
解析：（1）根据右手定则画等效电路图如图3所示，通过R的电流方向为C→D。

导体棒AB在切割磁感线运动的过程中，vA=ωr，vB=2ωr，

AB棒的平均速度为■=■=■，

根据法拉第电磁感应定律，导体棒上产生的感应电动势为E=Br■=■，

再根据闭合电路的欧姆定律，则通过电阻R的电流为I=■=■。

（2）根据能量守恒定律，外力的功率P等于安培力与摩擦力的功率之和，F安=BIrFf=μmg。

外力的功率为P=F■=（BIr+μmg）■=■+■。

点评：公式v=ωr中r指的是从圆心O点到棒上该点的距离，在转动切割中导体棒上各点的速度与半径r成正比，所以棒的平均速度可以用■=■求解，则感应电动势为E动=BL■；理解电磁感应现象中的能量守恒。

通过以上实例分析，电磁感应现象中产生感应电动势的方式各有不同，正确使用合适的公式求解是解题的关键，同时不能忽略两种感应电动势共存的情况。在解题过程中注意电路的分析和恒定直流电路相关规律应用，同时也要善于利用电磁感应现象中的能量守恒规律。